Ковалев И.В., Волкова Г.В. Автоматизированные системы конспект лекций
Подождите немного. Документ загружается.

процессора, а задачи выбирать в соответствии с их позицией в L разбиениях. В
подходе В первыми выбираются существенные задачи. Из этих двух подходов
эвристика А была быстрее; во всех тестируемых случаях эвристический подход
выдавал оптимальное решение.
Ограничения, рассмотренные ранее, были улучшены Фернандезом и Бусселом с
помощью подхода критического пути. Для некоторого графа существует путь от
входного узла до выходного, называемый критическим путем, который определяет
минимальное время выполнения для графа. Этот подход не требует равенства
времен задач. При заданном значении времени выполнения критического пути Т
ср
существует «интервал завершения» (определяемый самым ранним и самым поздним
временем начала выполнения) для каждой задачи в графе, в течение которого эта
задача должна быть завершена, и время ее выполнения не должно превысить Т
ср
.
В приближении к нижней границе количества процессоров Фернандез и Буссел
рассматривали целочисленные интервалы между 0 и Т
ср
. Внутри каждого из этих
интервалов задачи перемещены так, чтобы дать минимальное перекрытие внутри
интервала. Среднее число процессоров, требуемых в интервале, определяет
минимальное число процессоров, необходимых для этого интервала. Если все
интервалы исследованы, то максимальное среднее значение, округляемое в
большую сторону к ближайшему целому, представляет минимальное количество
процессоров, необходимых для обработки графа за минимальное время.
Похожие идеи использованы для определения минимального времени
выполнения с фиксированным числом процессоров. В течение каждого интервала
должно иметь место некоторое количество вычислений, чтобы убедиться, что общее
время выполнения не превышает Т
ср
. Если количество используемых процессоров
меньше некоторого минимума, то каждый интервал будет вносить количество
времени сверх того, что могло бы быть внесено, если ограничение по Т
ср
выполнено.
Максимальная нехватка времени, вносимая всеми интервалами, определяет
минимальное количество времени свыше Т
ср
, необходимого для обработки графа.
Позднее Буссел, Фернандез и Леви обращались к проблеме разработки
алгоритмов для минимизации числа процессоров, необходимых для выполнения
плана за определенное время, и для минимизации времени выполнения с
фиксированным числом процессоров. Полученные в результате планы получили
названия процессорно-оптимальных и оптимальных по времени планов
соответственно. Рассмотренная среда состояла из множества задач частичного
упорядочивания, неравных времен задач бесприоритетных прерываний активных
задач.
Попросту говоря, их алгоритм состоит в добавлении условий старшинства
(добавочных дуг) в первоначальный граф в те узлы, где число задач-кандидатов
превышает число процессоров. Результатом является распределение требований
процессора по всей длине графа без неблагоприятного воздействия на времена
выполнения. Как и для алгоритмов Рамамурти, Чанди и Гонзалеза, описанных выше,
фактическое описание и реализация алгоритма и его составных частей оказываются
значительно более трудными, чем основная идея, предпосылка, на которой основан
алгоритм. В обоих случаях это проявляется в виде значительного увеличения
времени вычислений даже на больших компьютерных системах. Альтернативный
110

метод – полный перебор – все равно является гораздо менее желательным.
Рамамурти и др. предлагают субоптимальные эвристические методы, а Буссел и др.
– альтернативные субоптимальные методы, которые могут выполняться в
интерактивном режиме. В обоих случаях лишний раз упоминается о трудности
получения оптимальных планов в общей среде планирования.
Лью и Янг разработали ограничения минимального времени завершения для
произвольного множества задач, когда не все задачи независимы, а процессоры не
обязательно являются идентичными.
(b)(a)
(c)
T
7
T
6
T
3
T
4
T
5
T
1
T
2
1
2
1 1
2 2
1
(d)
0 21 3 4
T
21
T
51
T
11
P
1
P
2
5 6
T
31
T
41
T
71
T
61
T
12
T
22
T
32
T
71
T
61
T
32
T
41
T
51
T
12
T
22
11 1
1
T
11
T
21
T
31
1 1 1
111
0 21 3 4
T
2
T
5
T
1
P
1
P
2
5 6 7
T
3
T
4
T
7
T
6
а – граф задач G; b – граф задач G
w
(w = 1);
c – оптимальный неприоритетный план для графа G;
d – оптимальный план для графа G
w
Рисунок 3.21 – Сравнение оптимальных приоритетных и неприоритетных планов
Сравнение приоритетных и неприоритетных планов.
Методы минимизации времени выполнения для некоторых особых случаев
были рассмотрены Кофманом и Грахамом в процитированной выше работе об
оптимальных неприоритетных двухпроцессорных планах. Точкой опоры в них
является возможность преобразования графа G с произвольными взаимно
соизмеримыми весами задач в граф G
w
с временами выполнения, равными w. Как и
раньше, w – самый большой вес, кратный всем весам задач в G. Если приоритетные
прерывания допускаются только в моменты времени, кратные w, то оптимальный
неприоритетный план для G может рассматриваться как оптимальный
приоритетный план для G. Например, на рисунке 3.21 показан случай увеличения
производительности разрешением приоритетных прерываний в конце каждого
единичного интервала (т. е. w = 1). Включение приоритетных прерываний в конец
каждого единичного интервала приводит к увеличению производительности на 117
%.
Кофман и Грахам заметили, что разрешение прерываний чаще, чем каждые w/2
единиц, не дает никакой выгоды, и показали, что для произвольного числа
процессоров m (
1m
) длина W
n
неприоритетного плана относится к длине
приоритетного плана как
mWW
pn
12
.
Минимизация среднего времени потока
111
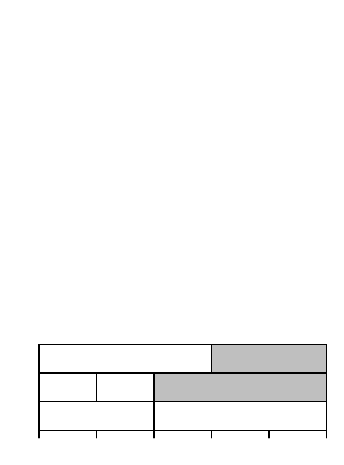
Рассмотрим задачу построения планов для множества независимых задач с
целью минимизации среднего времени потока. Ранее было показано, что показатель
производительности может быть минимизирован для набора идентичных
процессоров планированием задач в соответствии с SPT подходом. Однако здесь
рассмотрим неидентичные или гетерогенные процессоры. Приведенные результаты
говорят об усложнении процесса планирования. Эти соображения отражают
возрастающую необходимость многопроцессорных и распределенных
процессорных систем и полезность увеличения пропускной способности систем или
замены неисправных или устаревших компонентов.
В своей работе Бруно, Кофман и Сети приводят эффективный алгоритм
планирования независимых задач, уменьшающий среднее время выполнения
(среднее время потока). Так как рассматриваются неидентичные процессоры, то
использование отдельной величины для представления времени выполнения задач
больше не имеет смысла. Будем рассматривать время выполнения задачи на каждом
из процессоров. Удобным способом сделать это для случая m процессоров и n задач
является использование матрицы [T
ij
] размером m
n, в которой целые
неотрицательные величины T
ij
обозначают время выполнения задачи T
j
на
процессоре P
i
. Пример такой матрицы для пяти задач и трех процессоров:
32323
55141
64132
][
ij
T
.
Соответствующий оптимальный план показан на рисунке 3.22.
]n[T
]2[T
][T
ij
ij
ij
Q
.
0 21 3 4
T
4
T
1
P
1
P
3
5
T
2
P
2
T
3
T
5
Рисунок 3.22 – Оптимальный план, использующий алгоритм Бруно и др.
Из матрицы [T
ij
] формируется матрица Q размером nm
n, где множество n
элементов в матрице называется допустимым множеством, если в любой его строке
нет двух одинаковых элементов. Ценой этого множества называется сумма весов n
элементов. Тогда целью является поиск допустимого множества с наименьшей
возможной ценой. Можно формулировать данную задачу в виде транспортной
задачи и прийти к непереборному оптимальному решению.
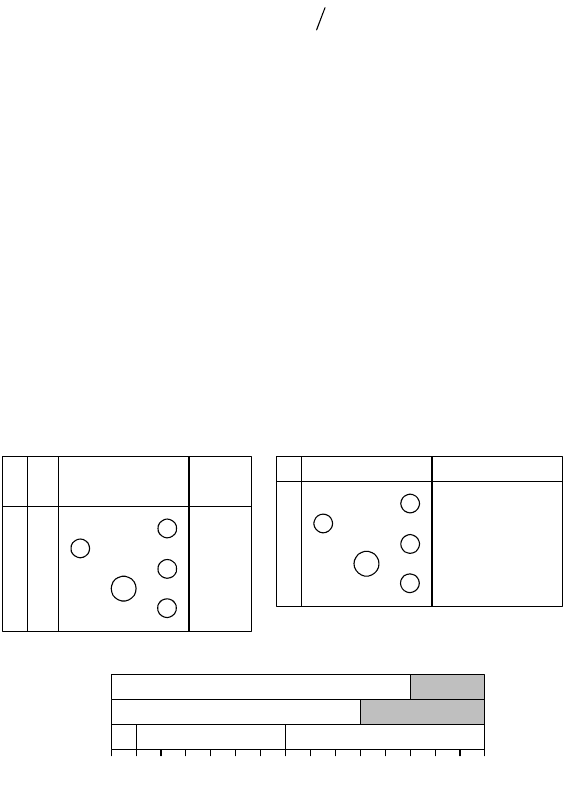
Если каждой задаче назначены приоритет или величина срочности w и принято,
что процессоры идентичны, то задача является NP-трудной. Однако для m
процессоров и n задач показано, что нижняя граница взвешенного среднего времени
потока F
w
(m) может быть определена как:
112
)1(])1()([)(
''
ww
FnmnmmF
,
где F
w
(1) является взвешенным средним временем потока с одним
процессором.
Оптимальное решение было использовано для создания простых эвристических
методов, обеспечивающих почти оптимальные планы со средним временем
завершения. Рассматривается n независимых задач, m неидентичных процессоров и
матрица P для описания времени обработки задачи i на процессоре j – P
ij
.
В первую очередь Кларк сделал вывод, что каждый элемент P
ij
может быть
выражен как «произведение времени, связанного с работой i, на показатель
эффективности, связанный с процессором j, т. е. P
ij
= p
i
w
j
». В разработанном
алгоритме матрица времен обработки и процессорных коэффициентов формируется,
как показано на рисунке 3.23, а. Причем времена обработки расположены в
следующем порядке
521
... ppp
.
(c)
0 42 6 8
T
4
T
1
P
1
P
3
10
T
2
P
2
T
3
T
5
12 14
(b)(a)
i
1
2
3
4
5
1 2 3
16
12
12
8
2
20
15
15
10
2.5
8
6
6
4
1
h
1
1
1
2
2
2
1
1
1
1
2
1
2
2
3
3
h
2
h
3
i
1
2
3
4
5
P
i
8
6
6
4
1
potential coefficients
1 2 3
machine
chosen
3
1
3
2
3
2
2
4
4
4
2.5
2.5
2.5
2.5
5
1
2
2
3
3
а – матрица времени обработки, эффективности работы и выбора машин;
b – альтернативный метод выбора машин; с – оптимальный план
Рисунок 3.23 – Алгоритм Кларка
Начиная с верхней строки матрицы, наименьшие коэффициенты обозначаются
кружком. Это говорит о том, что задача, находящаяся в первой строке матрицы
(задача 1 в этом примере), назначается процессору, который соответствует
отмеченному коэффициенту (процессор 3). Вторая строка матрицы формируется
копированием неотмеченных кружком коэффициентов из предыдущей строки и
увеличением значения отмеченных коэффициентов на соответствующее значение w
j
.
Повторив эту процедуру n-1 раз (с произвольным выбором в случае совпадений),
получаем план с оптимальным средним временем завершения. Оптимальный план
для этого примера и вычисление времени потока приведены на рисунке 3.23, b. В
другом варианте этого подхода вся матрица первоначально заполняется явными
временами обработки, а матрица коэффициентов формируется способом, похожим
на описанный выше. Пусть коэффициенты h
1
, h
2
, ..., h
m
в некоторой строке i
представляют возможные позиции соответствующих задач в последовательности из
трех процессоров, считая от конца плана. Тогда для минимального h
i
выбирается P
ij
,
отмечается кружком, а h
i
в следующей строке увеличивается на единицу (рисунок
3.23, с). Величина F для этого примера равна:
113

4581161211345,262
)(2)(3
1333534221
pwpwpwpwpwF
Так как не используются характеристики процессора, последний подход
является более общим, но это не гарантирует его оптимальности. Из-за его простоты
Кларк использовал этот подход в своей следующей работе, ссылаясь на него, как на
«быстрый и приближенный» (quick-and-dirty, QAD) алгоритм. Модификация этого
алгоритма, QAD* сортирует задачи на каждой машине с помощью SPT
упорядочивания, так как это гарантирует минимизацию времени потока на каждой
машине. Кларком доказано, что существует способ перенумерации задач
(перестановка строк в массиве времени обработки) такой, что QAD дает план с
минимальным временем потока и, соответственно, минимальным средним временем
потока.
Лью и Янг разработали алгоритм минимизации среднего времени потока на
множестве независимых задач для частного случая с одним процессором со
скоростью b или n стандартными процессорами. Например, этот алгоритм
позволяет сравнить производительность, учитывая соотношение среднего времени
потока на гомогенной системе из n + 1 стандартных процессоров, с негомогенной
системой, содержащей n стандартных процессоров и один процессор, который в 6
раз мощнее стандартного процессора.
5. Периодичные задачи при формировании процессов
Введем новые ограничения в дополнение к ранее принятым. Эти новые
ограничения представлены в форме классов ресурсов, периодичных задач с
жесткими границами и временных пределов реализации задач.
5.1. Ограничения на классы ресурсов
Решения, рассматриваемые до сих пор, были связаны, прежде всего, с
распределением процессоров. Вычислительные ограничения выражались в терминах
времени выполнения и отношений предшествования. Следовательно,
предполагалось, что процессор является единственным ресурсом, необходимым для
выполнения работ. Признание факта, что задаче кроме процессора могут
потребоваться дополнительные ресурсы, привело к исследованиям «систем с
ограниченными ресурсами», в которых предполагается потребность в различных
ресурсах, количество которых ограничено.
Указанная модель расширяет понятие стандартной модели, состоящей из
множества r задач неравной длительности, связанных отношением
предшествования, и выполняемых на неприоритетной основе набором из n
идентичных процессоров. Дополнительно предполагается наличие множества
ресурсов R={R
1
,...,R
S
}. Если задаче T
i
необходим ресурс R
j
, то это требование
принимается во внимание в течение всего периода выполнения задачи. Потребность
задачи T
j
в ресурсе R
i
обозначается через p
ij
(
1
ij
p0
). Положим r
i
(t) обозначает
общее количество ресурсов R
i
, которое используется в момент времени t. Тогда r
i
(t)
= Sum(p
ij
) для всех T
j
, выполняемых в момент времени t и
1)( tr
i
. Основная
114

проблема заключается в определении того, в какой степени использование
различных списков планов для этой модели влияет на время завершения w.
Предположим, что для двух произвольных списков L и L’ расширенная система
из n процессоров выполняет набор из r задач с результирующими временами
завершения w и w’ соответственно. Для такой среды предлагается следующее
решение:
при R={R
1
} (в системе существует только один вид ресурсов, отличных от
процессора)
nww '
;
при R={R
1
} и независимости всех задач
nww /13'
;
при R=(R
1
, R
2
,…, R
S
}, независимости задач и
rn
1'/ Sww
.
Общий смысл этих результатов заключается в том, что добавление ресурсов в
стандартную модель является причиной усиления ограничений на поведение в
наихудших случаях.
По существу используется та же модель за исключением того, что все задачи
для завершения требуют единичный интервал времени. Часто, используя эту
модель, получаем ограничения на количество задач, число процессоров и правила
формирования списка использованных планов. Показано, что эти алгоритмы ведут
себя хуже, когда устраняются ограничения на ресурсы.
Можно предположить, что отдельные задачи требуют минимального
количества памяти в дополнение к некоторому количеству времени обработки.
Тогда рассматривается система из m идентичных процессоров и n независимых
задач, причем каждый процессор связан с определенным устройством памяти
некоторой емкости. Когда процессор завершает выполнение задачи, в списке задач
выбирается первая задача, чьи требования памяти не превышают его собственного
объема. Для неприоритетной среды предлагаются ограничения и эвристические
стратегии выбора задач на основе требований времени и памяти одновременно.
Перейдем к рассмотрению периодичных задач при формировании
параллельных процессов.
Периодичные задачи рассматривались нами ранее в параграфе
однопроцессорных планов. Тогда для выполнения временных ограничений для
задач с более высокими приоритетами разрешалось приоритетное прерывание
периодичных задач. Теперь же рассматриваются неприоритетные
многопроцессорные планы для набора независимых периодичных задач.
Предполагается, что все задачи доступны одновременно. Целью является
минимизация числа процессоров, требуемых для выполнения ряда задач при
временных ограничениях на начало/конец выполнения заданий.
Пусть E
i
– максимальное время выполнения одной итерации задачи J
i
, а f
i
–
частота выполнения. Таким образом, каждой задаче J
i
соответствуют два параметра
J
i
:(f
i
, E
i
),
ni 1
, где n – количество включаемых в план задач. Период повторения
равен T
i
, величине, обратной f
i
. Рассмотрим два класса задач.
1) Если n задач с J
1
по J
n
распределены так, что f
i
> f
i+1
, то предполагается,
что f
i
= 2f
i+1
;
2) Допускаются задачи с любой частотой.
5.2. Периодичные задачи с бинарным частотным распределением
115
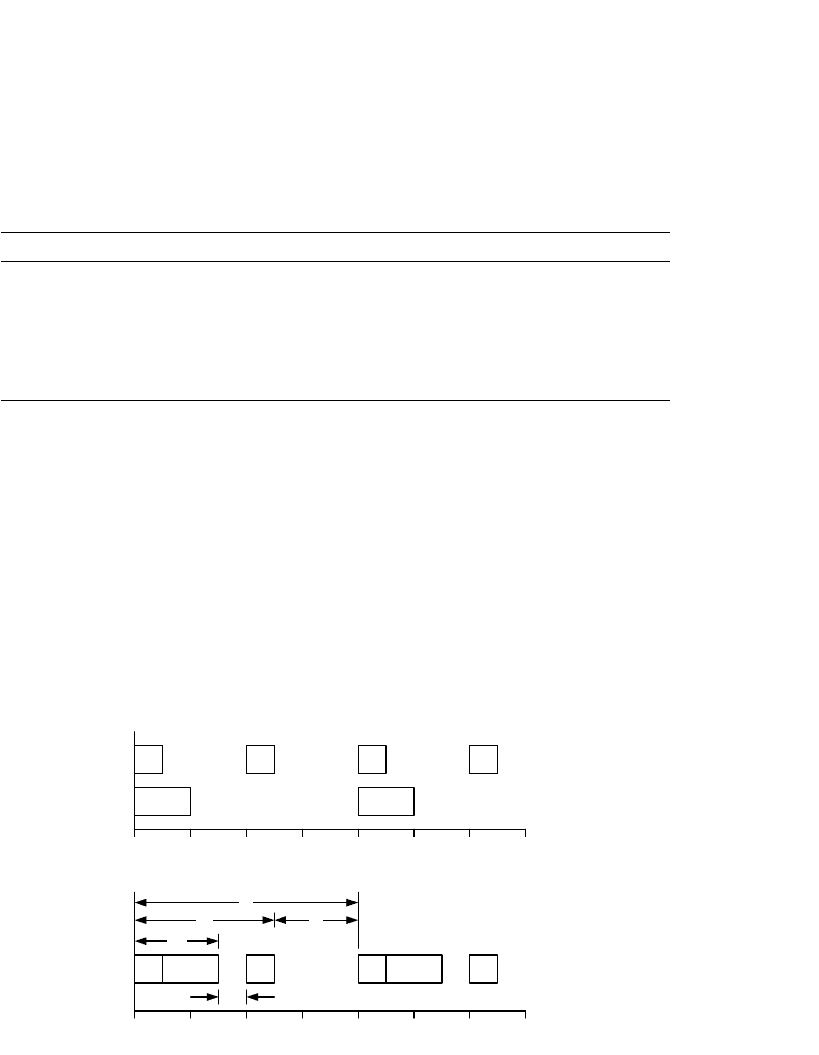
Множество задач, удовлетворяющих бинарному частотному распределению,
приведено в таблице 3.8. На рисунке 3.24, а, показаны задачи J
1
и J
2
,
спланированные на разных процессорах, а на рисунке 3.24, b показан план,
уменьшающий количество процессоров с двух до одного. Проблемой является
определение минимального количества процессоров без перебора всех возможных
альтернатив.
Заметим, что слияние двух задач, приведенное на рисунке 3.24, b, создает
новую периодичную задачу с периодом t
1
(равным 2T
1
) и временем выполнения е
1
(равным T
1
+ E
1
). Кроме того, имеются два промежутка с простоями: I
1
периодичный простой с длительностью t
1
- е
1
, и
1
2
принудительное время простоя
длинной I
1
- E
2
(обозначение
i
j
Δ
указывает, что принудительное время простоя
получается, когда J
j
объединяется с J
i
.)
Таблица 3.8 – Характеристики для множества задач с бинарным частотным
распределением
Задача Частота Период Время выполнения
J
1
1/4 4 1
J
2
1/8 8 2
J
3
1/16 16 1½
J
4
1/32 32 5
J
5
1/64 64 3
В процессе объединения остальных задач плана нет необходимости в
рассмотрении размещения задач в интервале принудительного простоя. Вместо
этого для этой среды план с минимальным числом процессоров формируется в
соответствии со следующим алгоритмом:
1) Пусть J
1
*, J
2
*,… – подмножество задач, назначенных процессорам P
1
, P
2
,….
Сначала J
1
*=J
2
*=…=
, а I
1
=I
2
=…=∞. Всякий раз, когда задача J
j
назначается
пустой J
i
*, I
i
= T
j
- E
j
;
2) Чтобы определить J
1
, необходимо найти наименьшее I такое, что
ii
IE
и
назначить J
i
к J
J
*.
(b)
(a)
0 42 6 8 10 12 14
J
1
J
1
J
1
J
2
J
1
t
1
e
1
I
1
T
1
J
2
1
2
116

а – временная диаграмма для первых двух задач из таблицы 3.8;
b – ослабление ограничений на число процессоров путем слияния задач
Рисунок 3.24 – Планирование периодичных задач с бинарным частотным
распределением
0 84 12
4
1
16 20 24 28 32 36 40 44 48 52 56
4
2 1 3 1 2 1 5 1 2 1 3 1 2 1 1 2 1 3 1 2 1 1 2 1 3
Рисунок 3.25 – Оптимальный план для задач из таблицы 3.8.
Оптимальный план для набора задач из таблицы 3.8 показан на рисунке 3.25.
Этот результат обобщается для случая, когда f
i
= k(f
i+1
), k – положительное целое
число больше 1.
5.3. Периодичные задачи с независимым распределением частоты
В этом параграфе рассматривается случай, когда устранена частотная связь
между задачами, принятая ранее. Как можно было бы ожидать, в таком виде задача
становится более сложной, а оптимальное решение не может быть найдено. Однако
были разработаны эвристические подходы и проведено их относительное сравнение
с применением моделирования. Эти подходы можно разделить на три группы.
1. В порядке уменьшения частоты.
Задачи располагаются в порядке уменьшения частоты и их назначение также
должно проходить в этом порядке.
2. В порядке уменьшения критерия загрузки.
Критерий загрузки задачи J
i
, обозначаемый L
i
, определяется следующим
образом: L
i
= E
i
/T
i
.
3. Сохранение минимальной длины критического интервала.
Критический интервал между двумя задачами определяется как минимальный
интервал между временем завершения первой задачи и временем начала
выполнения второй задачи в некоторой точке плана. Определение этого интервала
не включает первую итерацию обоих задач, где по определению начало выполнения
второй задачи немедленно следует за завершением первой задачи.
При тестировании данных методов, задачи разделялись на два класса. В 1-м
классе частоты задач кратны более чем двум базовым частотам, а во 2-м – не более
чем двум базовым частотам. Ни один из алгоритмов не показал значительного
превосходства над другими. Однако подход 2 исключительно хорошо показал себя
на задачах первого класса. Подход 3 лучше решает некоторые задачи второго
класса, а оба подхода 1 и 2 неплохо решают задачи, которые оказались трудными
для подхода 3. В этом нет ничего необычного, так как число процессоров,
необходимых для задач второго класса, было значительно меньше, чем для задач
первого класса.
117
Также были обнаружены некоторые интересные аномалии. Во многих случаях
обнаружилось, что уменьшение частот задач или времен их выполнения может
привести к увеличению количества требуемых процессоров. И наоборот, требуемое
количество процессоров может быть уменьшено увеличением частот задач или
времен выполнения, т. е., увеличивая загруженность процессора.
5.4. Учет пределов при формировании параллельных процессов
Ранее уже упоминался термин «планирование с учетом пределов» для среды,
состоящей из одного процессора и набора периодичных задач известной частоты и
периода. Теперь рассмотрим многопроцессорную систему, в которой задачи с
неравными временами выполнения связаны некоторыми отношениями
предшествования и выполняются без учета приоритетов.
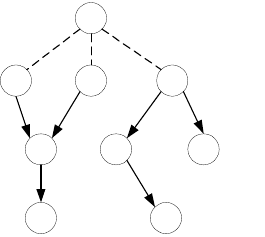
В частности, рассматривается случай, в котором задачи как терминальные, так
и нетерминальные требуют различного времени завершения. Пример графа,
удовлетворяющего этим требованиям, показан на рисунке 3.26. На этом рисунке
пара чисел вида A/B рядом с узлом обозначает задачу, чье время начала выполнения
равно А и которая должна быть выполнена за B единиц времени после начала
выполнения.
T
8
T
6
T
3
T
4
T
5
T
1
T
2
1020 10
T
0
0/0
15 15/30 10/45
T
7
5/50 5/45
Рисунок 3.26 – Граф с многочисленными временными ограничениями
Эвристическое решение этой задачи является разновидностью планов с
наидлиннейшим путем, рассмотренных ранее. Однако в этом случае большое число
наидлиннейших путей может быть определено для задач с пределами. Фактически
процедура является вариацией разбиения по последнему предшествованию для
случая с неравными временами задач и множественными пределами.
В своей работе по планированию с ограничениями Макнаутон рассмотрел
случай, когда в качестве пределов определены ограничения на каждую задачу и
потери в случае отказа. При задании так называемых абсолютных пределов задача
не имеет никакой цены, если она не завершена до заданного предела. В случае с
относительными пределами потери равны нулю до некоторой точки и монотонно
возрастают (как функция времени завершения) вне (выше) этой точки. Основной
вывод для многопроцессорного случая состоит в том, что все множество
независимых задач имеет ограничение в нулевой момент времени, т. е. все задачи
одновременно доступны и имеют равные приоритеты. Макнаутон показал, что для
этого случая нет необходимости в определении приоритетных прерываний, чтобы
минимизировать функцию потерь.
118

Итак, в данном параграфе рассмотрены некоторые из наиболее важных моделей
и алгоритмов формирования детерминированных наборов задач ИУС.
Предполагалось, что графы задач являются ацикличными, без ответвлений и что
времена выполнения задач точно известны. Тем не менее, следует упомянуть, что во
многих компьютерных системах эти предположения не имеют смысла. Баер
рассматривал некоторые из реализаций циклов и ветвей в графах. Чанди, наряду с
другими, рассматривает планы, в которых времена выполнения задач точно не
известны. Большинство работ Конвэя, Максвелла и Миллера посвящено так
называемой общей n-задачной m-машинной конвейерной проблеме.
Приведенные результаты показали, что эффективные оптимальные алгоритмы
могут существовать только в некоторых частных случаях, и предполагают
возможность активного исследования эвристических методов. Таким образом,
задачу построения детерминированных графов для использования в реальных
вычислительных средах ИУС можно считать выполненной. Результаты могут быть
также интересны и в рамках теории исследования операций с учетом
предположения о детерминированности процессов (что не всегда применимо на
практике). Единственным способом решения практических задач формирования
параллельных процессов может оказаться либо хорошо проверенный эвристический
алгоритм, либо некоторый статистический метод. Последний представляет собой
новый подход к решению проблемы.
Тема 3.6 Алгоритм оптимизации сетевых моделей методом случайного поиска
с пересчетом с переменной величиной шага
Рассматриваемая задача оптимизации на множестве сетевых моделей
заключается в формировании оптимального расписания выполненных операций в
ИУС, объединенных общими ограничениями на ресурсы.
1. Модель формирования оптимального плана
Итак, имеется N сетевых моделей процессов (планов), причем q-й план (q=
NI ,
) содержит множество V
q
логически взаимосвязанных между собой операций. Сами
возможные планы между собой не связаны. Для выполнения плана операций в ИУС
используются ресурсы L видов (либо невзаимозаменяемые между собой группы
исполнителей).
Предполагается, что каждая (i,j)
q
операция (работа) q-го плана, где i- начальное,
j- конечное событие работы, выполняется только одним видом ресурса, причем
известно каким. Множество работ q-го плана, выполняемых одним видом ресурса
обозначим как
).(
1
q
l
q
L
l
q
l
VVUV
Каждой операции (i,j)
q
ставится в соответствие: продолжительности
выполнения t(i,j)
q
, наиболее ранний момент начала t
рн
(i,j)
q
и наиболее поздний
момент окончания t
по
(i,j)
q
удельные денежные затраты a (i,j)
q
(затраты на единицу
времени выполнения работы). Для каждого q-го проекта плана известны
119
