Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

Application of Digital Speckle Pattern

Interferometry (DSPI) in Determination

of Elastic Modulus Using Plate Vibration

Chandra Shakher

and Rajesh Kumar

Laser Applications and Holography Laboratory,

Instrument Design Development Centre,

Indian Institute of Technology, Delhi

New Delhi – 110 016, India

Tel.: +91-11-2659-1432; Fax: +91-11-2686-2037

cshakher@iddc.iitd.ac.in, cshakher1949@hotmail.com

Department of Mechanical Engineering,

Sant Longowal Institute of Engineering and Technology,

(Deemed to be University; established by Government of India)

Longowal – 148 106 (Punjab), India

Abstract. Elastic material properties critically affect the vibration behavior of

structures. The value of natural frequencies changes due to change in the plate

constants/plate stiffness which is a function of elastic modulus. At each natural

frequency, the plate has a unique mode shape of vibration which can be easily

differentiated from mode shapes at other natural frequencies. In this paper, a

technique for the evaluation of the elastic modulus is proposed which is based on

the vibration analysis of the plate using digital speckle pattern interferometry

(DSPI) and Rayleigh method. Large numbers of experiments were conducted

on square aluminium plate for the boundary condition; one edge is fixed and

other edges free. The experimental result reveals that a single observation of fre-

quency at first torsional mode is sufficient to evaluate the elastic modulus for all

practical purposes. The evaluated experimental error was found to be less than

1%. Ease in sample preparation, simplicity in evaluation, non destructive nature

of the DSPI and speed of DSPI has good prospect to evaluate elastic modulus of

a material.

1 Introduction

Tensile test and bending test have been well established for determination of

mechanical properties of material [1]. But these methods are of destructive type

and suitable for bulk film materials. Optical techniques can be used to evaluate

330 C. Shakher and R. Kumar

elastic modulus for both bulk film and thin film materials [2-6]. Seebacher et al.

in their work used digital holography in evaluation of elastic modulus of silicon

microbeams. In their experiment, the cantilever beam was mechanically loaded by

a defined force in static manner at free end. The 3D-surface displacements were

measured and used in calculating elastic modulus [4]. Viotti et al. have proposed

an optical system which uses a spherical tip to introduce a permanent displace-

ment field to locally evaluate the elastic moduli of solid materials [5]. As vibration

behavior of structures is critically affected by elastic material properties, hence the

same can be used for estimation of elastic modulus in a non-destructive manner.

Recently, in 2007, evaluation of elastic modulus of cantilever beam using ESPI

and Euler–Bernoulli equation was demonstrated by Kang et al. [6]. The specimens

used for the elastic modulus experiment were of pure copper beam and cold rolled

carbon steel cantilever beams (ratio of length and width, a/b ≥10). But for the can-

tilever beam only bending modes are observed. The fringes in bending modes are

straight and directed in the direction parallel to the fixed edge at every resonance

frequency. This may lead to ambiguity in identifying the specific mode of vibra-

tion. Fringes generated due to the environmental perturbations may also create

ambiguity in measurement. Investigation of plate vibration has received consider-

able attention for academic research due to its wide range engineering applica-

tions. Speed of digital speckle pattern interferometry (DSPI) made it a powerful

tool for scanning and recording mode shape of vibration of plate [7-10]. Mode

shapes of vibration for square, rectangular and many more shapes under different

boundary conditions using DSPI were studied in detail by many investigators [9,

11-13]. Results from DSPI reveal that for different torsional and plate modes of

vibration, at each natural frequency, the plate has a unique mode shape of vibra-

tion and the fringes are not unidirectionally parallel to the fixed edge of the plate

(as in the bending modes). This reduces chance of ambiguity due to environmental

perturbation and human error in identifying specific mode shape.

A technique for evaluation of elastic modulus has been proposed in this paper

which is based on vibration analysis of plate using DSPI and Rayleigh’s method.

At resonance frequencies the harmonically vibrating plate has zero displacement

along nodal line and higher displacement at other points. In time-average sequen-

tial subtraction DSPI, the brightest fringe represents the nodal line. A large num-

ber of experiments were conducted on square aluminum plates for the boundary

condition one edge fixed and other edges free. The evaluation of elastic modulus

is compared with the supplied data. Ease of sample preparation, simplicity in

evaluation, nondestructive nature of experimentations, and speed of DSPI has high

prospective in evaluation of elastic modulus of a material.

2 Principle

2.1 Determination of Elastic Modulus Using the Concept of Plate Vibration

The study is based on transverse/out-of-plane vibration of the plate. Normal and

shear forces in the plane of the flat plate of uniform thickness are shown in Fig.1.

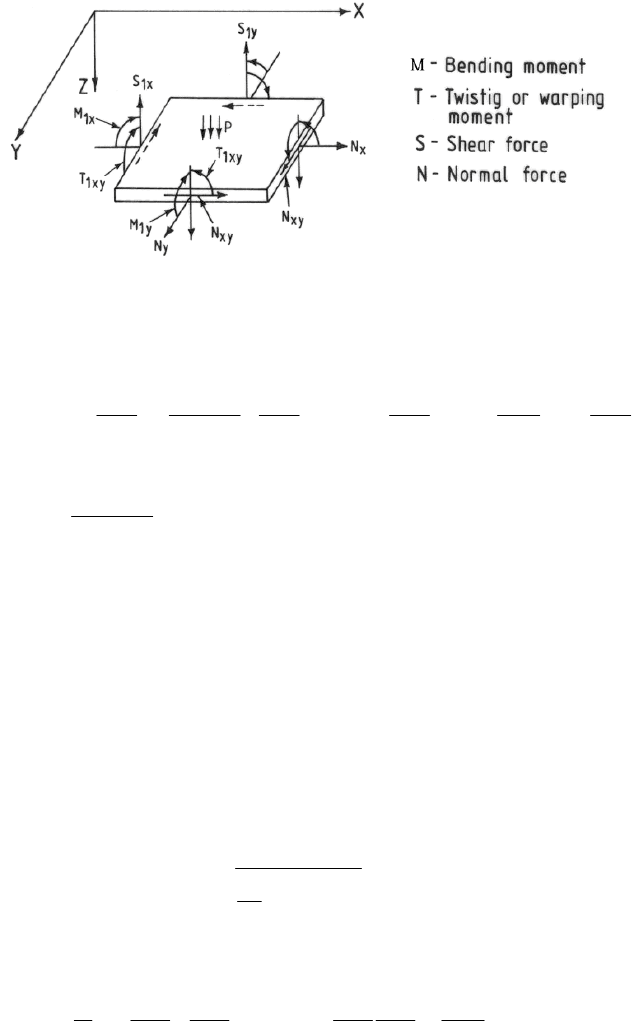
Application of DSPI in Determination of Elastic Modulus Using Plate Vibration 331

Fig. 1. An element of plate showing bending moments, normal and shear forces

Following equation relates the lateral deflection w to the loading on the plate

made of homogeneous isotropic material [14]:

NP)

y x

(DwD

∂

∂∂

∂

∂∂

∂

=∇

(1)

where,

)1(12

ν−

is the plate stiffness,

E is modulus of elasticity,

is the

thickness of the plate and

is Poisson’s ratio of the material of the plate and x

and y are spatial variable for the plate. The parameter

P is the loading intensity,

N is normal (in-plane) loading in the X -direction per unit length,

(in-

plane) is normal loading in Y-direction per unit length, and

the shear load pa-

rallel to the plate surface in the X- and Y-directions, per unit length.

The equation of free vibration of plate is more complicated to solve than one

governing the vibration of beam. By using an admissible mode function in Ray-

leigh’s method, an approximate expression for natural frequency is obtained. This

can be improved by using Ritz’s method [15] in which the natural mode shape

function is assumed in series form. For the mass density of the plate

, the Ray-

leigh’s method gives the following frequency equation:

∫∫

=ω

max

dxdy W

(2)

where ‘V’ is strain energy and is given by [14]

dxdy]})

(

)[1(2)

{(

∫∫

∂∂

∂

−

∂∂

ν−−+=

(3)

332 C. Shakher and R. Kumar

The Ritz method involves assuming

W , which is a function of x and y satisfy-

ing the necessary boundary conditions, to be of the form

...........)y,x(Wa)y,x(WaW

++=

. In which ...... ,W ,W

all satisfy at

least the geometric boundary conditions, and

....... ,a ,a

are adjusted to give a

minimum frequency. The first few natural frequencies obtained using these func-

tions for a square plate under different boundary conditions are given in literature

in terms of non-dimensional frequency parameters [14-16].

The non-dimensional frequency parameter is expressed as

haD/ ρω=ϖ

(4)

where, a is the side of the plate.

Putting the value of frequency in Hz (as

)2(f

πω= ), and plate stiffness, D

in the above equation, the modulus of elasticity can be written as

a)1(12

⎟

⎠

⎞

⎜

⎝

⎛

ρν−

(5)

Hence elastic modulus of a plate can easily be evaluated if the value of natural fre-

quency and corresponding mode shape of vibration are obtained from experiments.

3 Theoretical Background of Time-Averaged Specklegrams

The time-averaged processing is an extension of addition method. When object is

vibrating at a natural frequency much higher than the CCD frame refreshing time,

the resulting image is the superposition of the different position of the vibration. It

is called a time averaged specklegram and the modes of vibration corresponding to

brightest fringes. This is due to the modulation of intensity by the function J

(0th

order Bessel function) resulting from the integration of the vibration mode along

the frame time of the CCD

()

∫

dti

exp

In this case contrast is really poor. To enhance the fringe contrast, it is worth sub-

tracting from this the steady state specklegram or another time averaged speckle-

gram. The results given above by different method are still noisy.

3.1 Interferogram Formation

In DSPI, the primary interference between a speckle object beam and specular ref-

erence beam is recorded by CCD camera.

Application of DSPI in Determination of Elastic Modulus Using Plate Vibration 333

The specular reference beam has a complex amplitude

eAA

The speckle object beam has an amplitude

()

eAA

ψφ

In the above equation the total phase shift is splitted into two parts,

is slowly

varying function of position across the object and is spatially rapidly varying

function corresponding to randomly added phase of each speckle upon.

The phase is split into two parts so that high frequency speckles can be ensem-

ble averaged fringes. When the object and reference beam are combined in inter-

ferometer, the resulting slowly varying phase difference is defined as

φφφ

−=

These amplitudes and phases are the functions of x and y, the position across

the image of the speckle producing effect. When the deformations are observed,

the phase of the speckle field after perturbation of object is changed by

()

yx,

and the object field complex amplitude becomes

()()

φφψ

Δ++=

exp

ooo

iAA

(6)

() ()( )

[]

tyxyxIIIItyxI

roro

,,,cos2,,

φψ

+++=

(7)

()()()

tyxtyxtyx

,,,,,,

−=

(8)

It is assumed that beams are mutually coherent and have same state of polarization.

The phase

()

tyx

describes the optical path difference d(x, y) between

the object and reference beams.

() ()

yxdyx

(9)

‘

λ’ is the wavelength of light.

For rough surface

‘d’ varies with position by an amplitude which is much

greater than the wavelength of light. Thus ‘I’ takes the form of “speckle pattern”.

The instantaneous intensity ‘

I’ is recorded by the detector, which measures the

total energy (proportional to the intensity) incident at each detector point during

the exposure period ‘

T ’ is given by

()() () ()()

[]

⎭

⎬

⎫

⎩

⎨

⎧

++=

∫

dttyx

yxVyxIyxI

φψ

,cos

,1,,

(10)

334 C. Shakher and R. Kumar

Where

() ()

yxIyxIyxI

,,),( +=

≈

The form of the integral in eq. (10) depends on the type of illumination and sur-

face motion. We assume that during the exposure illumination is constant and that

a complete number of cycles of the harmonics surface motion, occur during the

exposure, ‘

T’. Eq. 10 can be re-written as

()() () ()

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

+= dJyxyxVyxIyxI

,cos,1,,

(11)

In the above equation the time-averaged interference pattern consist of a speckle

pattern in which visibility is modulated by Bessel function. Vibration nodes are

defined as loci of zero amplitude of vibration while anti-nodes describe the loci of

maximum amplitude of vibration. Antinodes occur between the nodes. Subsequent

maxima and minima of the zero order Bessel function are much lower and the

variation in the contrast of the speckles is very difficult to determine visually.

Thus, it is difficult to determine the vibration amplitude. To improve the fringe

contrast is essential to measure amplitude of vibration, which can be done by sub-

traction fringe formation.

3.2 Subtraction Fringe Formation

The term

⎟

⎠

⎞

⎜

⎝

⎛

contains useful information regarding amplitude of

vibration.

Consider acquiring two frames, each recorded when object is vibrating. The

first is represented by eq. 11 and the second with a ‘

α’ phase change introduced

between the frames.

For

α = π

() ( )

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

++= dJVIyxI

cos1,

πψ

(12)

Thus, the intensity difference is –

⎟

⎠

⎞

⎜

⎝

⎛

∝− dJVIII

cos.

(13)

Application of DSPI in Determination of Elastic Modulus Using Plate Vibration 335

The subtraction of two speckle patterns, corresponding to the states of the object,

will generally produce negative intensity values. It is usual to assign positive in-

tensity values at these points so that they do not appear black on monitor. There-

fore, intensity differences are squared and displaced on the monitor.

⎟

⎠

⎞

⎜

⎝

⎛

=−=Δ dJVIIII

(14)

The second option is to record first interferogram when vibration amplitude is zero

and other when vibration amplitude is non-zero. In this case, the intensity differ-

ence is,

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−=Δ dJVII

(15)

Equations 14 and 15 show that time averaged fringes are very different in appear-

ances. No longer they follow periodic form.

function indicates that brightest fringe corresponds to an argument zero (ze-

ro vibration amplitude). That is the brightest time averaged fringe corresponds to a

node of the motion. The fringes decline in brightness with the amplitude of vibra-

tion. Thus making it difficult to measure higher amplitudes where the depth of

modulation is poor.

(1 - J

)

function indicates that zero-argument fringe now corresponds to a

black fringe, and fringe sensitivity is halved as compared to

fringes. (1 - J

)

method enable rapid frequency scan, during which vibration modes can be identi-

fied as no new reference image required to be recorded during the scan. Once the

frequencies of interest have been identified, the high visibility

fringes can be

observed. To enhance the accuracy of the frequency measurement, it is better to

make fast scan nearby the resonance. This method shows its capability to accu-

rately measure vibration modes of plates and detect natural frequency with a good

accuracy.

4 Experiments and Results

Schematic of the DSPI set-up used for recording the fringe patterns of out-of-

plane/ transverse vibration of the plate is shown in Fig.2. The plate was excited by

a shaker (model number: EX 6 / 6.4, make: Prodera, France). A beam of 30 mW

He-Ne laser of wavelength 632.8 nm is split into two beams by a beam splitter

BS1. One of the beams illuminates the surface of the plate under study and the

other beam is used as the reference beam. The value of

for our experimental se-

tup is 1.938. The object beam is combined with the reference beam to form a

speckle interferogram that is converted into a video signal by a CCD camera. The

video analog output from HTC-550B/W CCIR CCD camera is fed to the PC-based

336 C. Shakher and R. Kumar

Fig. 2. Schematic of DSPI setup for measurement of out-of-plane vibrations.

image-processing system developed using National Instrument’s IMAQ PCI-1408

card. LabVIEW 5.0 based program [20] in graphical programming language was

developed to acquire, process and display the interferogram. To improve the con-

trast, the program implements accumulated linear histogram equalization after

subtraction of the interferograms. The time-average interferogram of the vibrating

plate over the frame acquisition period (1/30 second) is grabbed and subtracted

from the just previous time-average inteferogram in sequential subtraction man-

ner. The subtracted interferogram so obtained is displayed continuously on the

computer screen. Experiments were conducted on square plates made of alumin-

ium (physical properties as per the available data: Young’s modulus = 70 GPa,

Density = 2700 kg/m

, and Poisson’s ratio = 0.3). The plates were polished on op-

tical grinding machine to get the required flatness and smoothness of the surface.

To make the edge fixed, the plate was tightened with the help of strip and bolt to

have uniformly distributed stress at the edge of the plate. For the experiments car-

ried out with different objectives of vibration studies, to make an edge fixed, the

Application of DSPI in Determination of Elastic Modulus Using Plate Vibration 337

torque applied to tighten the plate was kept around an optimum value of 3Nm for

the setup [13]. There may be possibility of shift in natural frequencies as it is diffi-

cult to meet the boundary condition perfectly fixed at the edge of the plate. Func-

tion generator (model number: HP 33120A) was set to generate the sinusoidal sig-

nal and regulates the frequency and magnitude of the force of the exciter. A large

number of mode shapes according to change in excitation frequency were re-

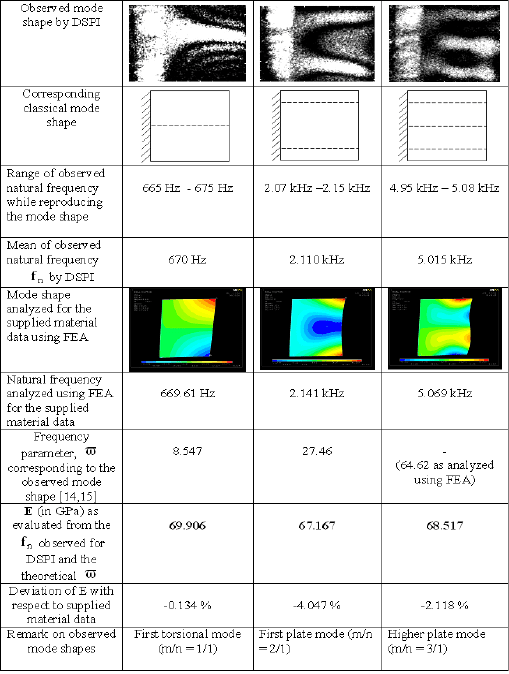
corded. Some typical speckle interferograms after noise removal showing the 1

torsion, 1

plate and higher plate mode shapes for a square plate (50 mm × 50 mm

× 0.8 mm) fixed at one edge and other edges being free are shown in table 1.

Table 1. Evaluation of elastic modulus based on data of first torsional and plate modes of

vibration for a square plate (50 mm × 50 mm × 0.8 mm) fixed at one edge and other edges

being free. Red is maximum deflection in positive direction, green is zero displacement

(nodal line) and blue is maximum deflection in opposite direction i.e. negative direction.

338 C. Shakher and R. Kumar

Evaluation of elastic modulus corresponding to the mode shapes are also tabu-

lated and shown in the same table. It was observed that for specific tightening

(3Nm torque) at edge of the plate, the mode shapes and corresponding frequencies

are reproducible. During each set of frequency scan for mode shapes, the band

width of frequency for a mode shape is approximately ±10Hz. After this band

width of frequency, symmetry of the mode shape is lost. Keeping other conditions

same, if the tightening at the edge is changed and frequency scan for mode shapes

is made, there is shift in natural frequencies but again for this tightening condition,

the natural frequencies are reproducible. Experiments were conducted time and

again by applying torques to tighten the plate close to 3Nm. It was observed that

the least variation (±5Hz) from the mean was for the first torsional mode. The

second least variation of around ±20Hz from the mean natural frequency was ob-

served for the first plate mode. Hence, for practical purposes, to evaluate elastic

modulus, data corresponding to the first torsional mode is more reliable and

reproducible.

The results were also verified using finite element analysis (FEA) package

(ANSYS 10.0). Natural frequency obtained using the FEA package corresponding

to the 1

torsional mode is 669.61 Hz. The variation of the mean value of the ex-

perimentally obtained frequency for 1

torsional mode with that of the FEA result

is only 0.04%. Although the data corresponding to the 1

torsional mode is suffi-

cient for evaluation of elastic constant as the variation in frequency for this case is

least ( less than 1%), one can be interested in evaluations based on two or three

least varying natural frequencies to have an average E. In these cases, the devia-

tion in E with respect to the supplied material data was -2.090% and -2.099% re-

spectively. Few more studies with different boundary condition are in process.

The preliminary results reveal that the method can be effectively used in determi-

nation of elastic modulus of the plate. Some typical observations under different

boundary conditions are shown in Table 2.

If we refer eq.5, for same material, computation of E is function of following

variables

),f,h,a(fE

ϖ=

(16)

Hence care must be taken while measuring dimensions of the plate along the

edges and locations for measurement of thickness of the plate. To have a uniform

thickness of plate, flatness is required to be maintained while polishing the plate.

Care during observing natural frequency, and maintaining plate clamping condi-

tions (it influences frequency parameter,

ϖ ) closer to the ideal one (which can be

achieved either by optimum tightening of strip and bolts, constraining more num-

ber of edges or by precisely controlled welding process) are also required to have

least absolute error in measurement.