Koren Y. The Global Manufacturing Revolution: Product-Process-Business Integration and Reconfigurable Systems

Подождите немного. Документ загружается.

10.4 EXAMPLE OF SYSTEM DESIGN

We demonstrate below how the Pascal Triangle in Figure 10.9 can be used in system

design. The example deals with designing a machining system that has an RMS

conﬁguration.

Raw parts are brought to a machining system after casting. The system contains

many CNC machines that perform all machining operations required to ﬁnish the part,

including milling, drilling, tapping, etc. A typical part of an automobile powertrain

system is shown in Figure 10.10. Note that the part has to be machined on several

faces, and that there are more than 200 machining tasks required to ﬁnish such a part,

and so it is impractical to include them all in this demonstration.

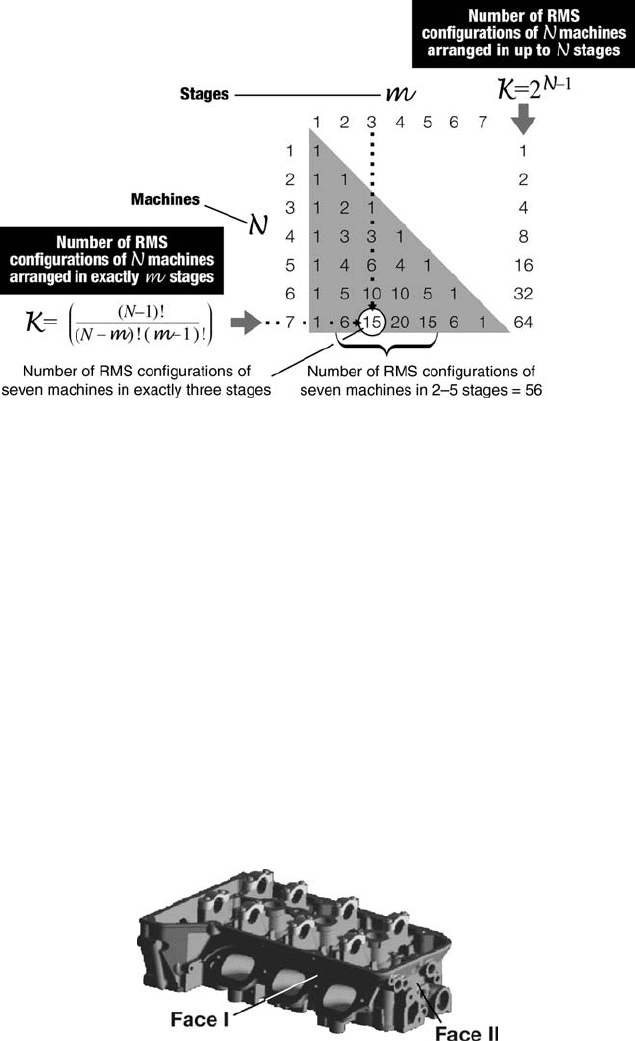
For simplicity, we will consider a simpler part that requires work on only two faces.

Each face requires a separate ﬁxturing, and theref ore the two faces must be machined

using two separate setups. Our simpliﬁed example requires only ﬁve machining tasks

Figure 10.9 The Pascal triangle is helpful in calculating the number of RMS

conﬁgurations.

Figure 10.10 An engine part after machining.

EXAMPLE OF SYSTEM DESIGN 261

to be completed. We will see that even for this simple example, the analysis is tedious

and lengthy. However, a methodic approach will be presented to whittle down the

range of possibilities, and make logical decisions based on facts and data to ﬁnd the

optimal system conﬁguration.

The problem that we would like to solve is deﬁned below.

10.4.1 Problem

Design a machining system to machine a part that requires t ¼ 12.2 minutes

machining time in ﬁve machining tasks. The execution times of the ﬁve tasks are

given in Figure 10.11. The required daily volume is Q ¼ 500 parts/day.

The working time per day is 1000 minutes. Assume machine reliability 100%

10.4.2 Solution

Producing 500 parts in 1000 minutes requires a cycle time of 2 minutes per part. The

ﬁrst step is to determine the minimum number of machines. Equation (10.1) yields

6.1 machines. But we must round the number to the next integer, which gives us N ¼ 7

machines.

According to Eq. (10.3), for seven machines and number of possible stages from 1

to 7, we are presented with 64 conﬁgurations to analyze. However, 64 conﬁgurations

is a large number that can be reduced by considering the speciﬁc tasks. Since the part

has only ﬁve machining tasks, the maximum number of stages can be just 5. The part

has two faces and each requires a different setup, and therefore the minimum number

of stages must be 2. If we are looking at the Pascal triangle in Figure 10.9, we can

see that for seven machines in the range between two and ﬁve stages there are only

56 conﬁgurations.

But do we still really have to compare 56 conﬁgurations? The answer is no!

Figure 10.11 Machining times.

262

SYSTEM CONFIGURATION ANALYSIS

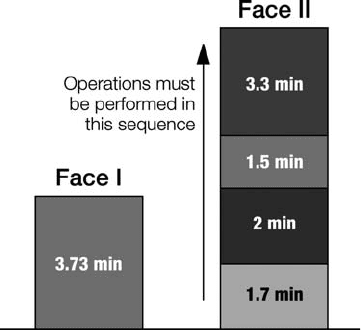
If the part has two faces, we may divide the system into two sub-systems—one for

Face 1 and the other for Face 2—and then design two separate sub-systems. In the sub-

system for Face 1 the machining time t is 3.7 minutes per part. According to Eq. (10.1)

the required number of machines for the ﬁrst Face is 2.

N ¼

500  3:7

1000

¼ 1:85Y2 machines ð10:5aÞ

In the sub-system for Face 2 the machining time t is 8.5 minutes per part. Acc ording

to Eq. (10.1) the required number of machines for the second Face is 5.

N ¼

500  8:5

1000

¼ 4:25Y5 machines ð10:5bÞ

Observing the Pascal triangle for these two sub-systems in Figure 10.12 shows only

15 possible conﬁgurations (rather than 56): one for Face 1, and 15 for Face 2.

1 ð1 þ 4 þ 6 þ 4Þ¼15

If the system contains just two stages, there is only one possible conﬁguration:

Stage 1 with two machines to work on Face 1, and Stage 2 with ﬁve machines for

Face 2.

If the system is comprised of three stages, there are four possible conﬁgurations.

For four stages, there are six possible conﬁgurations.

For ﬁve stages, there are four conﬁgurations: Stage 1 for Face 1, and four stages

for Face 2.

However, the formula for calculating the number of machines, Eq. (10.1), is based

on a perf ectly balanced system, and here the system is not necessarily balanced.

Therefore, several of these 15 possible conﬁgurations will not supply the demand of

Figure 10.12 Pascal triangle for the example.

EXAMPLE OF SYSTEM DESIGN 263

500 parts per day. Our next step is to determine which of the conﬁgurations will not

supply the demand and eliminate them.

For two stages there is only one possible conﬁguration, the one depicted in

Figure 10.13. In the ﬁrst stage, one part is produced every 1.85 minutes (between the

two machines), and in the second stage one part is produced (between the ﬁve

machines) every 1.7 minutes. The ﬁrst stage is the bo ttleneck, and dictates the cycle

time of the system is t

max

¼ 1.85 minutes. The number of parts per day is, therefore:

Q ¼ 1000/ t

max

¼ 540.

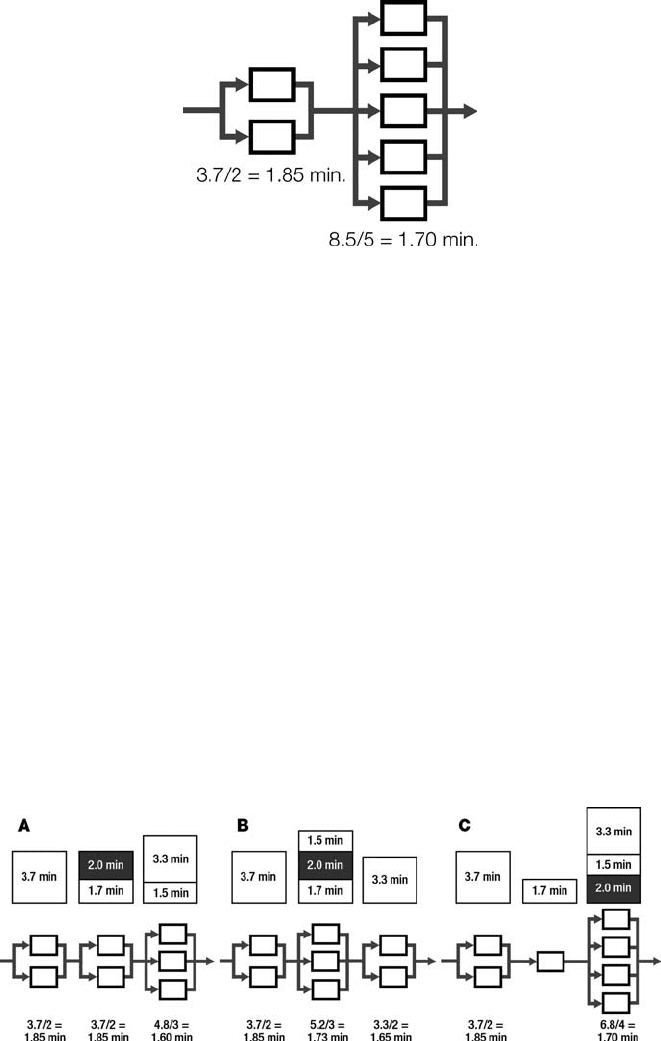
For three stages there are four possible conﬁgurations. However, only three of

them satisfy the cycle time constraint of t

max

 2 minutes. The three systems are

depicted in Figure 10.14. In these three cases the cycle time is t

max

¼ 1.85 minutes.

The fourth conﬁguration (not shown) has only one machine in the third stage,

which becomes a bottleneck with a cycle time of 3.3 minutes, which cannot satisfy the

required demand (a minimum cycle time of 2 minutes). Therefore, that conﬁguration

is unacceptable.

For four stages there are six possible conﬁgurations. However, three of them do

not satisfy the cycle time constraint of t

max

 2 minutes and have been omitted from

Figure 10.13 Two stages.

Figure 10.14 Conﬁgurations with three stages.

264

SYSTEM CONFIGURATION ANALYSIS

consideration. The three acceptable systems shown in Figure 10.15 all have a cycle

time of t

max

¼ 1.85 minutes. The three omitted conﬁgurations have only one machine

in the forth stage, which becomes a bottleneck with a cycle time of 3.3 minutes that

cannot produce the required demand.

For ﬁve stages there are four possible conﬁgurations, but only one of them is valid.

This one is shown in Figure 10.16. The bottleneck in this conﬁguration is in the third

stage, which yields a cycle time of 2 minutes. In the other three ﬁve-stage conﬁg-

urations, only one machine is placed in the ﬁfth stage, an arrangement that does not

satisfy the required cycle time.

We see that because of the cycle-time requirement, the number of conﬁgurations

is reduced from 15 to 8. Altogether, the number of possible RMS conﬁgurations to

consider was reduced from 64 to 8. Eight conﬁgurations is a manageable number to

compare.

In order to make a ﬁnal decision the designer has to compare at least the following

four factors (ranked by importance):

1. System throughput with reliability less than 100% (see next section)

2. Investment cost

3. Scalability—the increment of production capacity gained by adding a machine

4. Floor space, which may be roughly calculated by the conﬁguration length (i.e.,

number of stages, m) times its maximum width (i.e., the maximum number of

machines in a stage).

Figure 10.15 Conﬁgurations with four stages.

Figure 10.16 A conﬁguration with ﬁve stages.

EXAMPLE OF SYSTEM DESIGN 265

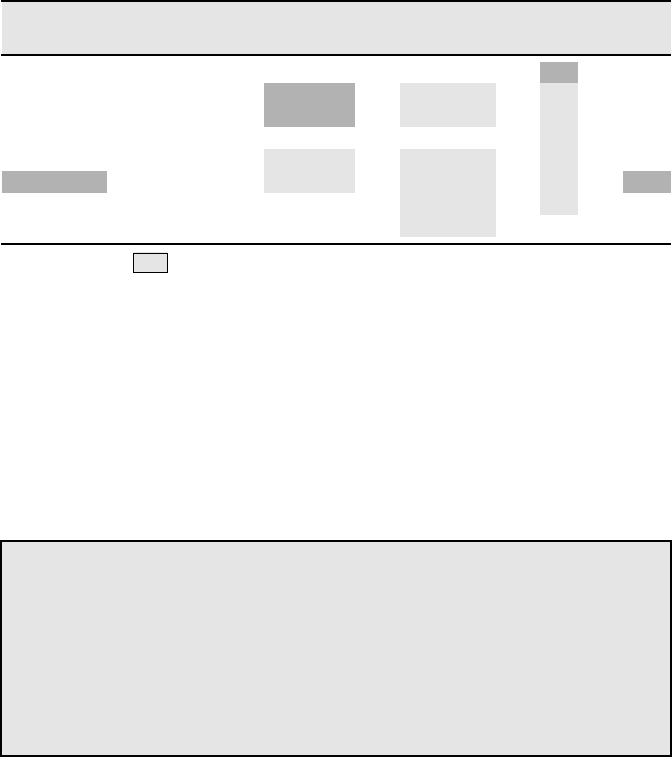
For our example these factors are compared in Table 10.1. The ranking in

Table 10.1 is subjective and depends on the weight that the designer (and company)

assigns to each factor (cost, scalability, etc). In our opinion, the conﬁguration that the

designer would most likely favor (Rank ¼ 1) is the one in Figure 10.13B (we will

further clarify this ranking at the end of the next section). By implementing

Conﬁguration 10.13B the throughput requirement (500 parts/day) is met and the

investment cost (machines and tooling) is acceptable. It has a good scalability factor

and will occupy a reasonable amount of ﬂoor space.

Important conclusions that we may draw from this example are

1. It is simple to calculate the minimum number of machines N needed in a

system based on the total processing time per part and the required daily

quantity.

2. The number of possible conﬁgurations is bounded by (i) the number of tasks

needed on the part and (ii) the number of faces on the part, and it is always

smaller than 2

N1

3. The number of possible RMS conﬁgurations is reduced dramatically when

considering the daily quantity requirement that must be met.

10.5 IMPACT OF CONFIGURATION ON PERFORMANCE

Differences in conﬁguration can have a profound impact on the performance of the

system in terms of throughput (jobs per hour), product quality, capacity scalability,

convertibility, and investment and operational costs. A systematic analysis of these

performance measures is presented below for different system conﬁgurations. For this

analysis we assume known machine-level reliability and process capability, as shown

in Figure 10.17.

The following performance measures are considered when selecting a system

conﬁguration:

TABLE 10.1 Comparison of Eight Conﬁgurations in the Example

Conﬁguration

in Figure Stages m Floor Space

Throughput

at R ¼ 100% Cost RANK

10.15 5 10 500 Low 7

10.14A 4 8 540 Med 6

10.14B 4 8 540 Med 5

10.14C 4 12 500 Med 8

10.13A 3 9 540 Med 2

10.13B 3 9 540 Med 1

10.13C 3 12 540 Med 4

10.12 2 10 540 High 3

Gray background ¼

Best;

; light gray background ¼ very good result compared with alternatives.

266 SYSTEM CONFIGURATION ANALYSIS

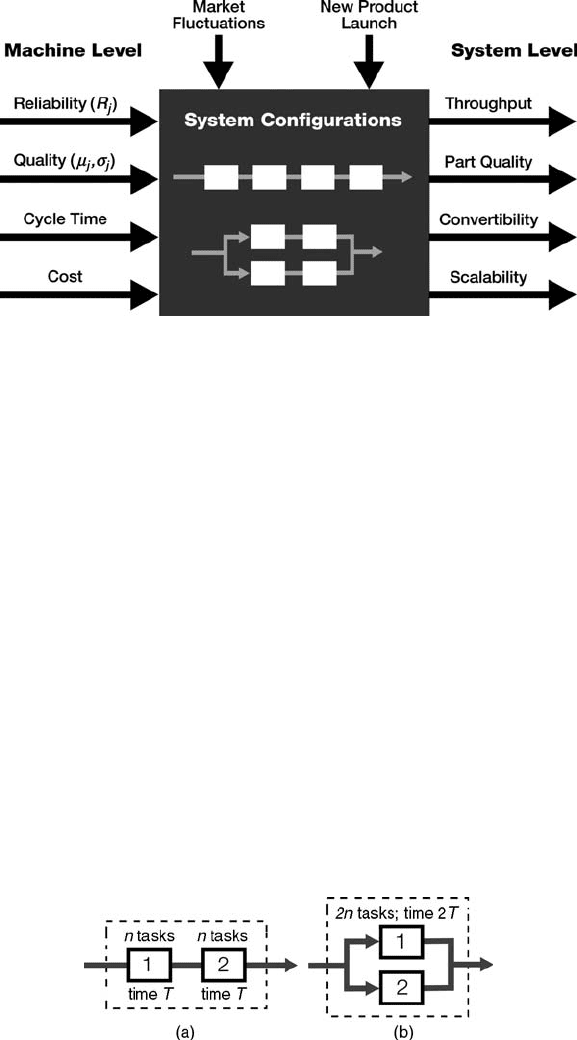
1. The initi al capital cost of the manufacturing system (Chapter 7)

2. Product quality (Section 10.5.1)

3. Throughput, which is dependent on equipment reliability (Section 10.5.2)

4. Capacity scalability (Section 10.5.3)

5. Convertibility—converting the system to production of a new product

6. The number of product types that the system can produce simultaneously.

Analytical or computational tools are necessary to evaluate these performance

measures. We will begin with some basic models of performance for a serial and

a parallel system with two machines, as shown in Figure 10.18. Each machine in the

serial conﬁguration produces one half of the total tasks, and in the parallel conﬁg-

uration, each machine produces the whole set of tasks. Both conﬁgurations produce

a part every T minutes.

To illustrate the analysis for more complex manufacturing system conﬁgurations,

we will then compare six conﬁgurations, with six machines each (Figure 10.19). We

will show that the preferred conﬁgurations are either d or e. Con ﬁguration b might be

selected only for special cases (e.g., where machine #6 performs a special, quick

process). If the system has to produce only one or two parts of the same family, we

Figure 10.17 Analysis approach.

Figure 10.18 Serial (a) and parallel (b) conﬁgurations with two machines.

IMPACT OF CONFIGURATION ON PERFORMANCE 267

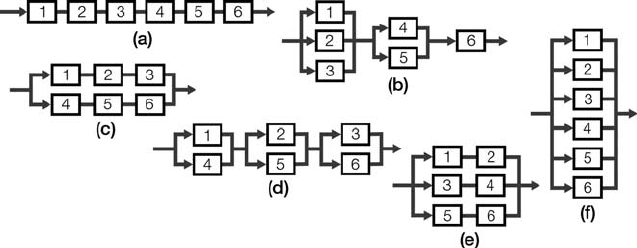
recommend selecting Conﬁguration d. If the part family is larger than tw o, we

recommend selecting Conﬁguration e, which will be easier to operate when simul-

taneously producing multiple products.

10.5.1 Product Dimensional Quality

Quality has many meanin gs. In this chapter we are mainly concerned with the

dimensional quality (accuracy) of the machined or assembled product. We deﬁne

quality here as

Dimensional Quality: Variation of a dimension from its designed intent.

The closer a dimension is to the design intent, the better the quality is.

With

volume production, the quality of the process can be measured by the mean deviation

from the design intent



y, and the standard deviation s

from the mean. The second

moment from the design intent,



þ s

, can be used as a single measure of the total

variation by combining the mean deviation and standard deviation together. This

deﬁnition is consistent with Taguchi’s quality loss function deﬁnition. In physical

units, the square root,

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



þ s

, is used.

Assume that the capab ility for each machine is given as m

; s



. For a serial

conﬁguration with two machines, if the operation of Machine 2 is dependent on that of

Machine 1, then the resulting quality will be given as

¼ s

þ s

ð10:6Þ

For a system with two machines in parallel, each machine will perform all the

operations in a single setup. As a result, the standard deviations for the parts from

each machine will be small compared with that from a serial conﬁguration.

However, because of the two part ﬂow paths, statistical “mixing” exists. As a

result, the total variation from the parallel conﬁguration could be larger, depending

on the differences in the process means of the two parallel machines. The difference

Figure 10.19 Six conﬁgurations with six machines.

268

SYSTEM CONFIGURATION ANALYSIS

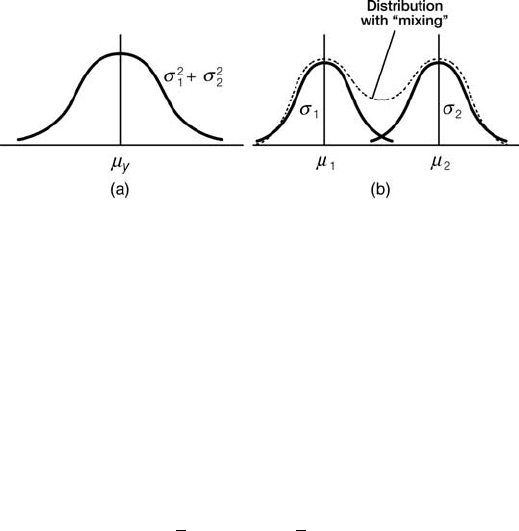
in quality, between serial and parallel conﬁgurations with two machines, is

illustrated in Figure 10.20.

The mean and standard deviation for parts coming out of a system with parallel

conﬁguration (Figure 10.20b) is calculated by the equations

¼ m

þ m

ðÞ=2 ð10:7Þ

and

þ s



m

ðÞ

ð10:8Þ

Systems with complex conﬁgurations can be analyzed in a similar way. In general,

Monte Carlo simulation methodologies can be applied in the analysis by using

random numbers to examine the manufacturing process.

Given the mean and

standard deviations of the machine, ﬁxture, and incoming part variation, the output

dimensions of a part or assembly can be predicted using process models.

For the six conﬁgurations shown in Figure 10.19, Monte Carlo simulation is used to

estimate the dimensional variation from each conﬁguration. Assuming that each

machine has a capability of setting the mean to within 10 mm, and has a repeatability

of 1 mm (one std. dev.). The resulting dimensional variations for the six conﬁgurations

are summarized in Figure 10.21. As can be seen from this ﬁgure, the conﬁguration in

Figure 10.19d has the largest quality variation because the number of part ﬂow paths is

the highest—8. The serial line (Figure 10.19a) has the best quality because there is

only one part ﬂow path and no “mixing” exists.

10.5.2 Reliability and Expected Throughput

The expected, calculated throughput depends on the reliability of the equipment (as

well as the processing rate and system balancing). The classical deﬁnition of

reliability was developed for aerospace and electronic systems. It measures the

probability of failure of the system. Similar deﬁnitions have been adopted for

manufacturing machines and equipment. A handbook developed by the Society of

Figure 10.20 Dimensional variation of parts from (a) serial conﬁguration and (b) parallel

conﬁguration.

IMPACT OF CONFIGURATION ON PERFORMANCE 269

Manufacturing Engine ers (SME) and the National Center for Manufacturing Sciences

(NCMS) deﬁnes reliability of machinery or equipment as the probability that the

machinery/equipment can perform continuously, without failure, for a speciﬁed

interval of time when operating under stated conditions.

This classical deﬁnition of machine reliability cannot be directly applied to

calculate manufacturing system reliability because in a parallel conﬁguration, when

one of the machines fails, the system can still function at a reduced level (50% of the

prior throughput, assumi ng that the two machines perform identical functions with the

same cycle time). (By contrast, in a system that has two identical computers in

parallel, if one computer fails, the system can still function at 100%.) Therefore, we

use the term “expected throughput,” which accounts for the probability of failure

and the corresponding throughput associated with each failure mode shown below.

For a system composed of two machines, there are four different system states: no

machine fails, one machine fails, and both machines fail. The probability and

productivity associated with each failure mode in a serial and a parallel system

are shown in Table 10.2, where R

and R

are the reliability of Machine 1 and

2 respectively.

Therefore, the expected throughput is the sum of the throughputs weighted by the

probabilities of the corresponding states.

The synchronous serial line expected throughput is

EP½¼1

þ 0

1R

ðÞþ0

1R

ðÞþ0

1R

ðÞ1R

ðÞ¼R

ð10:9Þ

Eq. (10.9) also expresses the reliability of the manufacturing system.

Figure 10.21 Dimensional variation resulted from the six conﬁgurations of Figure 10.17.

TABLE 10.2 Expected Throughput for Systems with Two Machines

Exp. Throughput

State Probability Serial Parallel

No machine fail R

Machine 1 fails R

(1  R

) 0 0.5

Machine 2 fails R

(1 – R

) 0 0.5

Both machines fail (1  R

)(1  R

)0 0

270

SYSTEM CONFIGURATION ANALYSIS