Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering

Подождите немного. Документ загружается.

On Numerical Issues in Time Accurate Laminar Reacting Gas Flow Solvers

holds, where w

is the numerical solution of the semi-discretization w

′

(t) = F(t,w)

on time t = t

. The validation and interpretation of the results is done in Section 6.

Right now, we are only interested in the performance of the various ODE integrators.

In Table 3, 4 and 5 numerical results for the various time integration methods,

with either the full or modiﬁed Newton iteration to solve the nonlinear systems, and

the relative errors with respect to a time accurate ODE solution, on some ﬁxed times

in the L

norm, are given. We used relative errors, because the solution contains

relatively small components. The user-speciﬁed quantity TOL to monitor the local

truncation error is taken equal to 10

−3

. For the time accurate ODE solution this

value was set to 10

−6

. We observe that for the global errors as presented in Tables

3, 4 and 5, the behavior is as expected.

For the unconditional positive EB time integration scheme it can be remarked

that modiﬁed Newton (see above) inﬂuences the positivity of the solution, i.e., the

number of rejected time steps due to negative species increases (compare Tables

3 and 4), and is in this case equal to 31. Rejected time steps due to negative en-

tries in the solution vector should be redone with smaller time steps, resulting in

a larger number of F evaluations (the number of Jacobian evaluations is approxi-

mately equal). Thus, as a result of an increasing number of Newton iterations, the

total computational costs increase.

For the BDF2 scheme (compare Tables 3 and 4), application of modiﬁed New-

ton strategy, as explained above, gives more satisfying results. From Table 4 it can

be concluded that for BDF2 an increasing number of cheaper Newton iterations is

computationally cheaper than factorizing the Jacobian in every Newton iteration.

With respect to the other higher order time integration schemes (see Table 5), we

note the following. ROS2 is the cheapest higher order time integrator for this CVD

process. For the IRKC scheme we see that both versions perform equally well. Since

there is no gain in efﬁciency by using ‘on the ﬂy’ stability conditions for the explicit

part, the more robust fully CFL-protected IRKC(full) is preferred.

Number of EB BDF-2

F 190 757

′

94 417

Linesearch

11 0

Newton iters

94 417

Rej. time steps

1 10

Acc. time steps

38 138

CPU Time

6500 30500

Relative error (t = 1.6 s /t = 3.2 s)

6.8·10

−3

/7.9 ·10

−4

2.2·10

−3

/ 1.4·10

−4

Table 3 Integration statistics for EB and BDF-2, with full Newton solver

With respect to positivity of the solution during transient simulations we note the

following. Omission of the reacting surface and thermal diffusion in the reaction

Jacobian gives very poor Newton convergence. We also observed that in this case

the solution conserves positivity for very small time steps only, even for EB. We

S. van Veldhuizen, C. Vuik, and C.R. Kleijn

Number of EB BDF-2

F 720 1786

′

84 163

Linesearch

39 33

Newton iters

463 1441

Rej. time steps

31 33

Acc. time steps

88 121

CPU Time

10800 17000

Relative error (t = 1.6 s/t = 3.2 s)

6.8·10

−3

/7.9 ·10

−4

2.2·10

−3

/ 1.4 ·10

−4

Table 4 Integration statistics for EB and BDF2, with modiﬁed Newton, as explained in Section

4.2

Number of ROS2 IRKC(ﬂy) IRKC(full)

F 424 429662 427911

′

142 2005 2008

Linesearch

0 50 30

Newton iters

0 17425 17331

Rej. time steps

2 729 728

Acc. time steps

140 1276 1284

CPU Time

8000 20000 19500

Relative error(t = 1.6 s/t = 3.2 s)

1.1·10

−3

/2.5 ·10

−4

1.8·10

−3

/8.3 ·10

−5

Table 5 Integration statistics for ROS2, IRKC(ﬂy), where stability for the explicitly integrated part

is tested for diffusion only, and IRKC(full), where stability conditions are forced for both advection

and diffusion, schemes.

conclude that for this CVD problem it is required to use the exact Jacobian, in which

also the derivatives of the reacting surface and thermal diffusion are included.

From the integration statistics presented in Tables 3-5 it is concluded that for

long time steady state simulations Euler Backward is, in spite of its ﬁrst order accu-

racy, the most efﬁcient time integrator. In [24] we concluded that the unconditional

positivity of Euler Backward is preferred over the conditional higher order methods

present in this section.

Off the shelf stiff ODE solvers like ODEPACK and DASSL do not test for posi-

tivity. The ODE suite ODEPACK is a collection of Fortran solvers for ODE systems.

This code and related codes, like LSODE and VODE, were the result of a long devel-

opment which started with Gear, see [7, 3]. The DASSL code, which is also suitable

for differential algebraic equations, employs the BDF formulas and is described in

detail in [2]. The purpose of their design is to integrate (stiff) ODEs by means of

BDF methods of the highest order possible in order to reduce computational costs.

These codes automatically select their order of accuracy based upon the time step

size and a user-deﬁned tolerance of required accuracy.

If these codes would test for positivity, then they should all switch back to ﬁrst

order accuracy to maintain the positive solutions. For this reason, we designed a

computationally efﬁcient Euler Backward solver. The remaining sections in this

chapter are devoted on the design of this solver. In particular we pay attention to

On Numerical Issues in Time Accurate Laminar Reacting Gas Flow Solvers

the robustness, and thus positivity, of the solver, and, of course, the reduction of

computational costs.

5 Design of the Euler Backward solver

The combination of the severe stiffness and the required positivity basically reduces

the time integration method to Euler Backward, as we have discussed in the previous

section. In practice, however, the use of Newton methods to iteratively solve the

nonlinear systems, does not guarantee positivity of the solution. In Section 5.1 we

propose a projected version of Newton’s method to overcome this problem, and

consequently, make the Euler Backward solver more robust.

Generally speaking, the large number of species results in huge nonlinear sys-

tems. The linear systems in Newton’s method are, consequently, also large. Second,

they are also sparse, which makes Krylov solvers suitable candidates to solve them.

Newton’s method combined with Krylov solvers are called Inexact Newton meth-

ods.

5.1 Globalized Inexact Projected Newton methods

In Inexact Newton solvers the Newton step, i.e. s

= −[F(x

)]

−1

F(x

), is approx-

imated by an iterative linear solver, which is in our case a preconditioned Krylov

method. The approximated Newton step s

has to satisfy the so-called Inexact New-

ton condition

kF(x

) + F

′

k ≤

kF(x

)k, (25)

for a certain ‘forcing term’

∈[0, 1). Note that the forcing term expresses a relative

stopping criterion for the Krylov method.

In [23] it has been concluded that for laminar reacting gas ﬂow simulations the

best choice for the forcing term is to base it on residual norms as

kF(x

k−1

, (26)

with

∈ [0,1) a parameter. The order of convergence of Inexact Newton with this

forcing term is two. In our experiments we put

= 0.5, which worked ﬁne.

It is generally known that Newton’s method converges towards a solution if and

only if the initial guess is in a neighborhood of this solution, see for instance [17].

Global convergence is enforced by implementing a line-search algorithm in the In-

exact Newton algorithm. This has been done as was proposed in [6].

In [23] we proposed an extension of the Globalized Inexact Newton method such

that it preserves positivity of species concentrations. We call this Globalized Inexact

Projected Newton (GIPN). As has been remarked in [23], repetitions of negative

S. van Veldhuizen, C. Vuik, and C.R. Kleijn

species concentrations can be observed in practice. The i-th entry of the projection

P is deﬁned as:

(x) =



if x

≥ 0.

0 if x

< 0.

(27)

In every Globalized Inexact Projected Newton step we test whether the projected

solution satisﬁes the sufﬁcient decrease condition, i.e.,

kF(P(x

+ s

))k > (1 −

(1 −

))kF(x

)k. (28)

For a comprehensive description and background of the GIPN methods we refer to

[23]. The present GIPN method, which is implemented in our code, is summarized

in Algorithm 1.

Algorithm 1 Globalized Inexact Projected Newton

1: Let x

max

∈ [0,1),

∈(0, 1) and 0 <

min

max

< 1 be given.

2: for k = 1, 2, . . . until ‘convergence’ do

3: Find some

∈ [0,

max

] and s

that satisfy

4: kF(x

) + F

′

k ≤

kF(x

)k.

5: while kF(P(x

+ s

))k > (1 −

(1−

))kF(x

)k do

6: Choose

∈ [

min

max

]

7: Set s

←

and

← 1 −

(1−

)

8: If such

cannot be found, terminate with failure.

9: end while

10: Set x

k+1

= P(x

+ s

11: end for

5.2 Preconditioned Krylov solver

Roughly speaking, there are two classes of Krylov solvers to solve large, sparse lin-

ear systems. On the one hand we have the class of GMRES solvers, and on the other

hand we have the Bi-CGSTAB solvers. In the numerical linear algebra community

it is well known that both methods have advantages and disadvantages. The linear

systems in our code result from spatial discretization on a structured grid. Conse-

quently, the matrix-vector multiplication is cheap to implement. Bi-CGSTAB needs

two matrix-vector multiplications per linear iteration and needs seven vectors in

memory. GMRES, however, needs only one matrix-vector multiplication, but needs

more vectors in memory. Because the matrix-vector multiplication is cheap, we use

from a memory usage point of view, the Bi-CGSTAB method.

The partial derivatives of the stiff and highly nonlinear reaction terms in eq. (1)

cause ill-conditioned Jacobian matrices. In Figure 4 the typical order of magnitude

of the condition-number of the Jacobian is shown as a function of (real) time (in

seconds).

On Numerical Issues in Time Accurate Laminar Reacting Gas Flow Solvers

If the eigenvalues of a matrix A are not clustered, it probably has a large condi-

tion number. It is well known that solving ill-conditioned linear systems with Krylov

solvers, leads to bad convergence or divergence of the Krylov method. Fast conver-

gence can be achieved by multiplying the A with a preconditioner M

−1

, such that

the eigenvalues of AM

−1

are efﬁciently clustered in comparison with those of A.

For the simulations in the present paper, Krylov solvers without preconditioning are

ruled out, because the condition numbers of the Jacobian matrices are far too large

to expect Bi-CGSTAB convergence at all.

As a ﬁnal remark before we discuss a set of suitable preconditioners, we want

to emphasize on the following rule of thumb. The partial derivatives of the reac-

tion terms, which contribute considerably to the large condition numbers, should be

inverted in order to reduce the condition number of the preconditioned systems. Fur-

ther, we mention that the ordering of unknowns and equations inﬂuences both the

performance and construction of a preconditioner. In the present paper, we consider

only the alternate blocking per grid point ordering, in which the unknown species

concentrations are ordered per grid point. The corresponding non-zero pattern of the

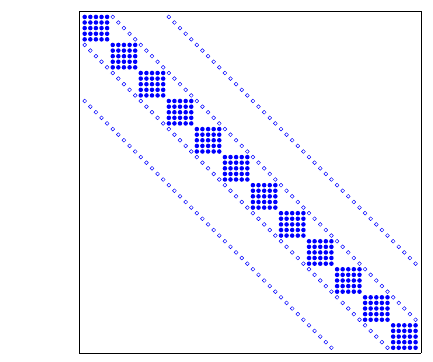
Jacobian is shown in Figure 5.

Fig. 4 Condition-number of the Jacobian as function of time (in seconds)

For the acceleration of the internal linear algebra problem in Algorithm 1, the

following preconditioners are compared:

• Incomplete factorization without ﬁll-in, denoted as ILU(0),

S. van Veldhuizen, C. Vuik, and C.R. Kleijn

Fig. 5 Non-zero structure of the Jacobian for the alternate blocking per grid point ordering. The

partial derivatives of the chemistry terms in Eq. (1) are represented by dots, and the super- and sub-

diagonals marked by circles are the off-diagonal discretized advection-diffusion terms in Eq.(1).

• Lumped Jacobian: a relatively good approximation of the Jacobian, which also

is easy to invert, can be obtained by adding all off-diagonal elements related to

the same species of a row to the main diagonal element, see [23],

• Block D-ILU: a block version of the D-ILU preconditioner, see for instance, [19],

• Block diagonal: omitting off-diagonal blocks gives an easy invertible block-

diagonal structure that resembles the Jacobian quite well.

A comprehensive discussion on these preconditioners combined with the GIPN

method can be found in [23]. In this paper we restrict ourselves to the conclusions

drawn in [23]. In terms of efﬁciency the incomplete factorization based precondi-

tioners perform excellent. Taking into account other arguments like the number of

Jacobian evaluations, the total number of linear iterations, positivity and robustness,

makes the block D-ILU preconditioner, combined with GIPN, the best precondi-

tioner for this class of problems.

6 Numerical results

Numerical experiments are done with the Euler Backward solver as presented in the

previous section. In all experiments we used block D-ILU as preconditioner. The

numerical tests are done for the two models of the CVD process of silicon from

silane, as presented in Section 3, on three different grid sizes. The simulations are

done on a grid with n

= 35 grid points in radial direction and n

= 32 grid points in

axial direction, an n

= 35 by n

= 47 grid and an n

= 70 by n

= 82 grid. For all

On Numerical Issues in Time Accurate Laminar Reacting Gas Flow Solvers

grid holds that the grid points in radial direction are equidistant. The grid points in

axial direction have a gradually decreasing grid spacing towards the wafer surface.

For the ﬁnest grid, i.e., the 70×82 grid, the axial distance from the wafer to the ﬁrst

grid point equals 1 ·10

−6

m, and thereafter the grid spacing will gradually increase

∆

z = 5 ·10

−3

m for z ≥ 0.04 m. For the coarsest grid the distance between the

wafer and the ﬁrst grid point is 2.5·10

−4

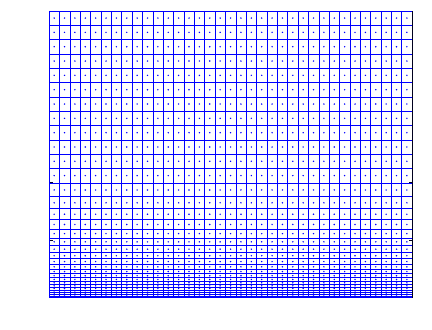
m. The 35 ×32 grid is illustrated in Figure

0 0.025 0.05 0.075 0.1 0.125 0.15 0.175

0.02

0.04

0.06

0.08

0.1

r(m)

z(m)

Fig. 6 Computational 35 ×32 grid. Species mass fractions are computed in the cell centers (rep-

resented as dots).

First, we present and discuss the integration statistics for the time accurate tran-

sient simulations of both chemistry models introduced in Section 3. Thereafter,

some time accurate results and their validation are presented.

6.1 Discussion on the integration statistics

For all simulations in this section, of which we present integration statistics, holds

that the simulations run from inﬂow conditions until the steady state solution is

reached. In all these simulations we allow the maximum number of time steps to

be 1000. With respect to the number of allowed Newton iterations per time step

we remark the following. The strongly nonlinear reaction terms sometimes cause

difﬁculties in ﬁnding the correct search direction. More speciﬁc, in the time frame

right before steady state is reached, we experienced that to ﬁnd the correct search

direction might take a few extra Newton iterations. Therefore, the maximum number

of Newton iterations is set to 80.

S. van Veldhuizen, C. Vuik, and C.R. Kleijn

Further, it has to be mentioned that in this paper time accurate transient results

are shown for different wafer temperatures varying from 900 up to 1100 K. Because

of the large activation energies of some of the reactants (see Table 1 and 2), such

temperature differences lead to large qualitative and quantitative differences in the

solutions. The behavior and the integration statistics of the computational method

is, however, not inﬂuenced by the wafer temperature. Therefore, we will restrict

ourselves to present the integration statistics for one wafer temperature per compu-

tational grid.

In Table 6 relevant integration statistics are listed for the 7 species and 5 reactions

model of Section 3.1. For this problem the grid size has no large inﬂuence on the

total number of Newton iterations. The effect of different grid sizes is reﬂected in

the number of linear iterations and CPU time. Due to the quality of the block D-ILU

preconditioner, no rejected time steps are observed in these simulations. Weaker

preconditioners can result in rejected time steps due to Newton divergence and/or

negative species concentrations, see [23].

Due to its stronger nonlinearity, the number of Newton iterations increases for the

17 species and 26 gas phase reactions CVD model, see Table 7. Again, the block D-

ILU preconditioner shows excellent performance with respect to positivity and fast

Bi-CGSTAB convergence. However, for the ﬁnest grid, with more grid cells in the

reaction zone, the semi-discrete problem is considerably stiffer than for the other

two grids. This greater stiffness is especially reﬂected in the increasing condition

numbers of the Jacobian, which are no longer easily cancelled by the preconditioner.

This explains the relatively large number of linear iterations on the ﬁnest grid, see

Table 7. When a ‘weaker’ preconditioner is used in this case, it is not possible to do

a complete simulation from inﬂow conditions until steady state, due to many time

step rejections caused by Newton divergence [23].

With respect to the total computational costs of these simulations the follow-

ing has to be remarked. Since in almost any case the required accuracy of the ap-

proximated linear solutions is low, the Bi-CGSTAB algorithm converges in a small

amount of iterations. However, when the stiff chemistry comes into play and an ac-

curately approximated linear solution is needed, the Bi-CGSTAB algorithm needs

to overcome a stagnation phase in order to obtain superlinear convergence. In the

stagnation phase the Ritz values belonging to the ‘bad’ eigenvalues have not fully

converged to the eigenvalues of the preconditioned system. If they have, then these

‘bad’ eigenvalues do not contribute to the effective condition number, and, hence,

Bi-CGSTAB converges superlinearly to the solution.

Note that accurate linear approximations are only needed when the steepest de-

scent direction is found in Newton’s method. In the ﬁrst few Newton iterations the

required accuracy of the linear solutions is relatively low [23] and thus are the costs

of constructing the Jacobian more important than the costs of the preconditioned

Bi-CGSTAB solver to ﬁnd an approximation of the linear solution.

On Numerical Issues in Time Accurate Laminar Reacting Gas Flow Solvers

Table 6 Number of operations for the 7 species and 5 reactions problem on three computational

grids. The wafer temperature is different for each computational grid.

Grid size 35 ×32 35 ×47 70×82

Wafer temperature 1000 K 950 K 900 K

Newton iters 80 89 91

Line search 9 6 7

Total linear iters 430 1,137 1,003

CPU time (sec) 140 230 690

Table 7 Number of operations for the 17 species and 16 reactions problem on three computational

grids. The wafer temperature is different for each computational grid.

Grid size 35 ×32 35 ×47 70×82

Wafer temperature 1000 K 950 K 900 K

Newton iters 93 148 306

Line search 4 28 96

Total linear iters 718 859 2,144

CPU time (sec) 320 470 4,175

6.2 Model validation and time accurate solutions

Correctness of our steady state solution, obtained after long time integration, is val-

idated against the steady state solution obtained with the software of Kleijn [15].

The solver of Kleijn [15] computes the steady state solution of the system of species

equations (1). The approach followed in [15] is to march through the computational

domain from grid point to grid point and solving (1) by a time-relaxation algo-

rithm. Kleijn’s approach is robust, but computationally inefﬁcient. All simulations

presented in this paper are test cases where the wafer is not rotating.

In Figure 7 steady state mass fraction proﬁles are presented for some selected

species, as well as the ones obtained by Kleijn [15], for a wafer temperature equal to

1000 K. In this case, the total steady state deposition rate of silicon at the symmetry

axis as found by Kleijn [15] is 1.92

, whereas we found a deposition rate of

1.93

. Both values compare excellently to those obtained with the well-known 1-

dimensional CVD simulation code SPIN within the Chemkin family [5]. In Figure

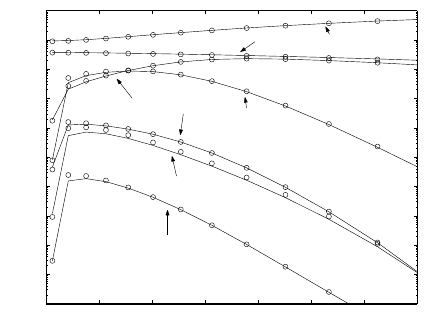
8 transient deposition rates are presented for some selected species, as well as the

transient total deposition rate. It can be seen that the time dependent behavior of

these deposition rates is monotonically increasing and stabilizes when the solution

is in steady state. Also shown are the steady state deposition rates obtained with the

software of Kleijn [15], which are in very good agreement with our current results.

In Figure 9 we present transient total deposition rates for simulations with wafer

temperatures varying from 900 K up to 1100 K. The time dependent behavior of

all deposition rates is monotonically increasing until the species concentrations are

in steady state. Note that the relative contributions of the various silicon containing

species to the total deposition rate is a function of the wafer temperatures, with

the relative contribution of Si

increasing with increasing temperature, and the

S. van Veldhuizen, C. Vuik, and C.R. Kleijn

relative contribution of H

SiSiH

decreasing with increasing temperature. In Figure

10 the species concentrations of SiH

for wafer temperatures T

= 900 K and T

1100 K are shown. We see that for T

= 1100 K the concentrations of SiH

are

much higher along the reacting surface than for T

= 900 K. Note that in Figure

10 the legends of both concentration ﬁelds differ two orders of magnitude. For the

species concentrations of H

SiSiH

, which are shown in Figure 11, we see that the

concentration of H

SiSiH

for T

= 1100 K is nearly zero along the wafer. This

results in a relatively small contribution of H

SiSiH

to the deposition rate.

In Figure 12 the transient behavior of the gas phase chemistry can be seen quite

clearly. At time t = 0.5 s we see that reactive silane is entering the reactor from the

top, but has not reached the reactive susceptor surface. At an inlet velocity of 0.1

m/s and a distance between the inlet and the susceptor of 0.1 m this actually takes

1 s. This is conﬁrmed by Figure 8 and 9, in which it can be seen that deposition

does not start until t ∼ 1 s. A couple of seconds later at time t = 5 s, when the CVD

process is almost in steady state, we see that along the reacting surface almost all

silane molecules either have been decomposed into volatile reaction products, or

have been adsorbed to the susceptor surface to form a solid silicon ﬁlm (see Figure

12).

Figure 13 shows radial proﬁles of the total steady state deposition rates for both

of Kleijn’s steady state computations [15], and our steady state results obtained

with the Euler Backward solver as discussed in Section 5, for wafer temperatures

varied from 900 K up to 1100 K. Again, the agreement is excellent for all wafer

temperatures. For all studied temperatures, the steady state growth rates obtained

with the present transient solution method were found to differ less than 5% from

those obtained with Kleijn’s steady state code.

0 0.002 0.004 0.006 0.008 0.01 0.012 0.014

−12

−11

−10

−9

−8

−7

−6

−5

−4

−3

−2

Height above Susceptor (m)

Species Mass Fractions (−)

SiH

SiSiH

SiH

Fig. 7 Axial steady state concentration proﬁles along the symmetry axis for some selected species.

Solid lines are Kleijn’s solutions [15], circles are long time steady state results obtained with the

present transient time integration methods.