Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering

Подождите немного. Документ загружается.

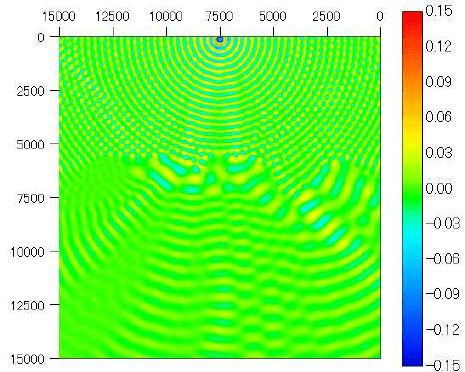
Shifted-Laplacian Preconditioners for Heterogeneous Helmholtz Problems

Fig. 11 Solution of the scaled Sigsbee problem with ABL, frequency 5Hz.

5 Conclusion

In this paper, we have discussed the ingredients of a robust and efﬁcient iterative

solver for heterogeneous high wavenumber Helmholtz problems. A preconditioned

Bi-CGSTAB solver has been developed in which the preconditioner is based on a

shifted Laplacian with a complex-valued shift. We have shown that it is possible

to work with fourth-order ﬁnite differences, both in the discrete original problem,

as well as in the preconditioner. An absorbing boundary layer improves the quality

of the solution signiﬁcantly and does not pose difﬁculties to the solution method

proposed. We have focused on fourth-order discretizations mostly obeying a linear

relation between the wavenumber and the mesh size, kh = 0.8, here.

The fourth-order accurate shifted Laplacian preconditioner can be approximated

by one V(0,1)-cycle of multigrid. In the multigrid preconditioner, we have com-

pared a point-wise Jacobi smoother with an ILU(0) smoother and we included an

AMG-based prolongation scheme. This enables us to choose a small imaginary shift

parameter (β

= 0.4) in the preconditioner, which improves the solver’s conver-

gence (especially for high wavenumbers on ﬁne meshes). The generalization to 3D

is straightforward; the parallelization of this solver requires, however, some consid-

erations as an ILU smoother is not easily parallelized.

Acknowledgment The authors would like to thank Shell International Exploration

and Production and Philips for their ﬁnancial support to this BTS project. Further-

more, they would like to thank Y.A. Erlangga, Ch. Dwi Riyanti, A. Kononov, M.B.

C.W. Oosterlee, C. Vuik, W.A. Mulder, and R.-E. Plessix

van Gijzen for their input in the project. In particular, we would also like to thank

S.P. MacLachlan and N. Umetani for their contribution to this article, as the present

article relies on paper [57] of which they are the co-authors. N. Umetani performed

some additional numerical experiments, especially for this paper.

References

1. T. AIRAKSINEN, E. HEIKKOLA, A. PENNANEN, J. TOIVANEN, An algebraic multigrid

based shifted-Laplacian preconditioner for the Helmholtz equation. J. Comp. Physics, 226:

1196–1210, 2007.

2. R. E. A

LCOUFFE, A. BRANDT, J. E. DENDY JR., J. W. PAINTER, The multi-grid method

for the diffusion equation with strongly discontinuous coefﬁcients, SIAM J. Sci. Comput., 2

(1981), pp. 430–454.

3. A. B

AMBERGER, P. JOLY, J.E. ROBERTS, Second-order absorbing boundary conditions for

the wave equations: A solution for the corner problem. SIAM J. Numer. Anal., 27: 323–352,

1990.

4. A. B

AYLISS, C. I. GOLDSTEIN, E. TURKEL, An iterative method for Helmholtz equation, J.

Comput. Phys., 49 (1983), pp. 443–457.

5. A. B

AYLISS, C.I. GOLDSTEIN E. TURKEL, On accuracy conditions for the numerical com-

putation of waves. J. Comput. Phys., 59: 396–404, 1985.

6. M. B

ENZI, D. BERTACCINI, Block Preconditioning of Real-Valued Iterative Algorithms for

Complex Linear Systems, October 2006, revised September 2007, 21 pages. To appear in IMA

Journal of Numerical Analysis.

7. M. B

OLLH

OFER, M. GROTE, O. SCHENK, Algebraic multilevel preconditioning for

Helmholtz equation, In: Proc. Europ. Conf. on Comput. Fluid Dynamics (ECCOMAS CFD

2006), Egmond aan Zee, The Netherlands, Sept. 5-8, 2006.

8. A. B

RANDT, Multi-level adaptive solutions to boundary-value problems. Math. Comput. 31:

333–390, 1977.

9. A. B

RANDT, S. TA’ASAN, Multigrid method for nearly singular and slightly indeﬁnite prob-

lems, in Proceedings EMG’85 Cologne, Multigrid Methods II, W. Hackbusch, U. Trottenberg,

eds., Springer, Berlin, 1986, pp. 99–121.

10. A. B

RANDT, I. LIVSHITS, Wave-ray multigrid methods for standing wave equations. Elect.

Trans. Numer. Anal. 6: 162–181, 1997.

11. W.L. B

RIGGS, V.E. HENSON, S.F. MCCORMICK, A multigrid tutorial: SIAM, Philadelphia,

USA, 2000.

12. I. D

UFF, S. GRATTON, X. PINEL, X. VASSEUR, Multigrid based preconditioners for the nu-

merical solution of two-dimensional heterogeneous problems in geophysics. Intern. J. Com-

puter Math., 84(8):1167–1181, 2007.

13. J. C

LAERBOUT, Imaging the Earth’s interior, Blackwell Science Inc., 1985.

14. H. R. E

LMAN, O. G. ERNST, D. P. O’LEARY, A multigrid method enhanced by Krylov

subspace iteration for discrete Helmholtz equations, SIAM J. Sci. Comput., 23: 1291–1315,

2001.

15. B. E

NGQUIST, A. MAJDA, Absorbing boundary conditions for the numerical simulation of

waves, Math. Comput., 31: 629–651, 1977.

16. Y.A. E

RLANGGA, C. VUIK, C.W. OOSTERLEE, On a class of preconditioners for the

Helmholtz equation, Appl. Numer. Math., 50 (2004), pp. 409–425.

17. Y.A. E

RLANGGA, C. VUIK, C.W. OOSTERLEE, Comparison of multigrid and incomplete

LU shifted-Laplace preconditioners for the inhomogeneous Helmholtz equation. Applied

Num. Math. 56: 648-666, 2006.

18. Y.A. E

RLANGGA, C.W. OOSTERLEE, C. VUIK, A novel multigrid based preconditioner for

heterogeneous Helmholtz problems. SIAM J. Sci. Comput. 27: 1471-1492, 2006.

Shifted-Laplacian Preconditioners for Heterogeneous Helmholtz Problems

19. Y.A. E

RLANGGA, Advances in Iterative Methods and Preconditioners for the Helmholtz

Equation Archives Comput. Methods in Engin., 15: 37-66, 2008.

20. M. B.

VAN GIJZEN, Y. A. ERLANGGA, C. VUIK, Spectral Analysis of the Discrete

Helmholtz Operator Preconditioned with a Shifted Laplacian SIAM J. Sci. Comput., 29: 1942-

1958, 2007.

21. A. G

EORGE, J.W. LIU, Computer solution of large sparse positive deﬁnite systems, Prentice-

Hall, New Jersey, 1981.

22. S.G

HEORGHE, On Multigrid Methods for Solving Electromagnetic Scattering Problems. PhD

Thesis, Univ. Kiel, Germany, 2006.

23. J. G

OZANI, A. NACHSHON, E. TURKEL, Conjugate gradient coupled with multigrid for an

indeﬁnite problem, in Advances in Comput. Methods for PDEs V, 425–427, 1984.

24. W. H

ACKBUSCH, Multi-grid methods and applications. Springer, Berlin, 1985.

25. E. H

EIKKOLA, S. M

ONK

A, A. PENNANEN, T. ROSSI, Controllability method for acoustic

scattering with spectral elements, J. Comput. Appl. Math., 204(2): 344-355, 2007.

26. E. H

EIKKOLA, S. M

ONK

A, A. PENNANEN, T. ROSSI, Controllability method for the

Helmholtz equation with higher-order discretizations. J. Comp. Phys., 225(2): 1553-1576,

2007.

27. F. I

HLENBURG, I. BABUSKA, Finite element solution to the Helmholtz equation with high

wave numbers. Comput. Math. Appl., 30: 9-37, 1995.

28. K. I

TO, J. TOIVANEN, A Fast Iterative Solver for Scattering by Elastic Objects in Layered

Media. Appl. Numerical Math., 57: 811-820, 2007.

29. C.-H. J

O, C. SHIN, J.H. SUH, An optimal 9-point, ﬁnite-difference, frequency space, 2-D

scalar wave extrapolator, Geophysics 61(2): 529–537, 1996.

30. R. K

ETTLER, Analysis and comparison of relaxation schemes in robust multigrid and pre-

conditioned conjugate gradient methods. In:W. Hackbusch, U. Trottenberg (eds.), Multigrid

methods, Lecture Notes in Mathematics 960: 502–534, Springer, Berlin, 1982.

31. M. K

HALIL, Analysis of linear multigrid methods for elliptic differential equations with dis-

continuous and anisotropic coefﬁcients. Ph.D. Thesis, Delft University of Technology, Delft,

Netherlands, 1989.

32. S. K

IM, S. KIM, Multigrid simulation for high-frequency solutions of the Helmholtz problem

in heterogeneous media, SIAM J. Sci. Comput. 24: 684–701, 2002.

33. D. L

AHAYE, H. DE GERSEM, S. VANDEWALLE, K. HAMEYER, Algebraic multigrid for

complex symmetric systems, IEEE Trans. Magn., 36 (2000), pp. 1535–1538.

34. A. L. L

AIRD, M. B. GILES, Preconditioned iterative solution of the 2D Helmholtz equation.

Report NA 02-12, Comp. Lab., Oxford Univ., 2002.

35. B. L

EE, T. A. MANTEUFFEL, S. F. MCCORMICK, J. RUGE, First-order system least-squares

for the Helmholtz equation, SIAM J. Sci. Comput., 21 (2000), pp. 1927–1949.

36. S.S. L

I, X.W. PING, R.S. CHEN, A Kind of Preconditioners Based on Shifted Operators to

Solve Three-Dimensional TVFEM Equations In: Int. Symp. on Microwave, Antenna, Propa-

gation and EMC Technologies for Wireless Communications, 842-844, 2007

37. Q. L

IAO, G.A. MCMECHAN, Multifrequency viscoacoustic modeling and inversion. Geo-

physics 61(5): 1371–1378, 1996.

38. S.P. M

ACLACHLAN, C.W. OOSTERLEE, Algebraic multigrid solvers for complex-valued

matrices, SIAM J. Sci. Comput., 30:1548-1571, 2008.

39. K.J. M

ARFURT, Accuracy of ﬁnite-difference and ﬁnite-element modeling of the scalar and

elastic wave-equations, Geophysics, 49: 533-549, 1984.

40. W.A. M

ULDER, R.-E. PLESSIX, A comparison between one-way and two-way wave-

equation migration, Geophysics, 69: 1491–1504, 2004.

41. W.A. M

ULDER, R.-E. PLESSIX, How to choose a subset of frequencies in frequency-domain

ﬁnite-difference migration, Geophys. J. Int. 158: 801–812, 2004.

42. O.V. N

ECHAEV, E.P. SHURINA, M.A. BOTCHEV, Multilevel iterative solvers for the

edge ﬁnite element solution of the 3D Maxwell equation. Comp. Mathem. Applications.

doi:10.1016/j.camwa.2007.11.003, to appear 2008.

C.W. Oosterlee, C. Vuik, W.A. Mulder, and R.-E. Plessix

43. S. O

PERTO, J. VIRIEUX, P. AMESTOY, J.Y. L’EXCELLENT, L. GIRAUD, B. BEN HADJ ALI,

3D ﬁnite-difference frequency-domain modeling of visco-acoustic wave propagation using a

massively parallel direct solver: A feasibility study, Geophysics, SM195-SM211, 2007.

44. R.-E. P

LESSIX, A Helmholtz iterative solver for 3D seismic-imaging problems, Geophysics,

72: 185–194, 2007.

45. P. P

OULLET, A. BOAG, Incremental unknowns preconditioning for solving the Helmholtz

equation. Num. Methods Partial Diff. Equations, 23(6): 1396-1410, 2007.

46. R.G. P

RATT, Seismic waveform inversion in frequency domain. Part I: theory and veriﬁcation

in a physical scale domain, Geophysics, 64: 888–901, 1999.

47. C.D. R

IYANTI, Y.A. ERLANGGA, R.-E. PLESSIX, W.A. MULDER, C.W. OOSTERLEE,

C. V

UIK, A new iterative solver for the time-harmonic wave equation, Geophysics 71: 57-

63, 2006.

48. C.D. R

IYANTI, A. KONONOV, Y.A. ERLANGGA, C. VUIK, C.W. OOSTERLEE, R-E

LESSIX W.A. MULDER, A parallel multigrid-based preconditioner for the 3D heterogeneous

high-frequency Helmholtz equation. J. Comp. Physics 224: 431-448, 2007.

49. J.W. R

UGE, K. ST

UBEN, Algebraic Multigrid (AMG). In: S.F. McCormick (ed.), Multigrid

Methods, Frontiers in Appl. Math., SIAM Philadelphia, 5: 73–130, 1987.

50. I. S

INGER, E. TURKEL, High Order Finite Difference Methods for the Helmholtz Equation,

Comp. Meth. Appl. Mech. Eng. 163:343-358, 1998.

51. I. S

INGER, E. TURKEL, A Perfectly Matched Layer for the Helmholtz Equation in a Semi-

inﬁnite Strip. J. Comput. Phys. 201 (2004) 439-465.

52. Y. Saad, M.H. Schultz, GMRES: A generalized minimal residual algorithm for solving non-

symmetric linear system, SIAM J. Sci. Comput., 7: 856–869, 1986.

53. Y. S

AAD, Iterative Methods for Sparse Linear Systems. SIAM, Philadelphia, 2003

54. U. T

ROTTENBERG, C.W. OOSTERLEE, A. SCH

ULLER, Multigrid, Academic Press, London,

2001.

55. E. T

URKEL, Numerical Methods and Nature. J. of Scientiﬁc Computing, 28 2/3: 549-570,

2006.

56. E. T

URKEL, Numerical difﬁculties solving time harmonic equations, in Multiscale Compu-

tational Methods in Chemistry and Physics, A. Brandt, et. al., eds., IOS Press, Tokyo, 2001,

pp. 319–337.

57. N.U

METANI S.P.MACLACHLAN, C.W. OOSTERLEE, A multigrid-based shifted-Laplacian

preconditioner for a fourth-order Helmholtz discretization. Working paper, Delft Univ. Techn.

Delft, the Netherlands, 2008. Submitted for publication.

58. H.A.

VAN DER VORST, Bi-CGSTAB: a fast and smoothly converging variant of Bi-CG for

the solution of nonsymmetric linear systems, SIAM J. Sci. Comput., 13: 631-645, 1992.

59. X. W

EI, H. P. URBACH, A. J. WACHTERS, Finite-element model for three-dimensional op-

tical scattering problems. J. Opt. Soc. Am. A, 24: 866-881, 2007.

60. P. W

ESSELING, An introduction to multigrid methods. John Wiley, Chichester, 1992.

61. R. W

IENANDS, C. W. OOSTERLEE, On three-grid Fourier analysis for multigrid, SIAM J.

Sci. Comput., 23 (2001), pp. 651–671.

62. G. W

ITTUM, On the robustness of ILU smoothing. SIAM J. Sci. Comput. 10: 699–717, 1989.

63. P. M.

DE ZEEUW, Matrix-dependent prolongations and restrictions in a blackbox multigrid

solver, J. Comput. Appl. Math., 33: 1–27, 1990.

64. P.M.

DE ZEEUW, Incomplete line LU as smoother and as preconditioner. In: W. Hackbusch,

G. Wittum (eds.), Incomplete decompositions (ILU) - algorithms, theory, and applications.

Vieweg, Braunschweig, 215–224, 1993. Int. J. Num. Methods in Fluids 20: 59–74, 1995.

On Numerical Issues in Time Accurate Laminar

Reacting Gas Flow Solvers

S. van Veldhuizen, C. Vuik, and C.R. Kleijn

Abstract The numerical modeling of laminar reacting gas ﬂows in thermal Chemi-

cal Vapor Deposition (CVD) processes commonly involves the solution of advection-

diffusion-reaction equations for a large number of reactants and intermediate species.

These equations are stifﬂy coupled through the reaction terms, which typically in-

clude dozens of ﬁnite rate elementary reaction steps with largely varying rate con-

stants. The solution of such stiff sets of equations is difﬁcult, especially when time-

accurate transient solutions are required. In this study various numerical schemes

for multidimensional transient simulations of laminar reacting gas ﬂows with ho-

mogeneous and heterogeneous chemical reactions are compared in terms of efﬁ-

ciency, accuracy and robustness. One of the test cases is the CVD process of silicon

from silane, modeled according to the classical 17 species, 26 reactions chemistry

model for this process as published by Coltrin and coworkers [4]. It is concluded

that, for time-accurate transient simulations the conservation of the non-negativity

of the species concentrations is much more important, and much more restrictive

towards the time step size, than stability. For this reason we restrict ourselves to

the ﬁrst order, unconditionally positive Euler Backward method. Since positivity of

the solution is very important, the use of Newton methods to solve the nonlinear

problems is only feasible in combination with direct solvers. When using iterative

linear solvers, it appears that the approximate solutions may have small negative

elements. To circumvent this, we introduce a projected Newton method. Choosing

the best preconditioners, combined with our projected Newton method, enables us

S. van Veldhuizen

Delft University of Technology, Delft Institute of Applied Mathematics and J.M. Burgerscentrum,

Mekelweg 4, 2628 CD Delft, The Netherlands, e-mail: s.vanveldhuizen@tudelft.nl

C. Vuik

Delft University of Technology, Delft Institute of Applied Mathematics and J.M. Burgerscentrum,

Mekelweg 4, 2628 CD Delft, The Netherlands, e-mail: c.vuik@tudelft.nl

C.R. Kleijn

Delft University of Technology, Department of Multi Scale Physics and J.M. Burgerscentrum,

Prins Bernardlaan 6, 2628 BW Delft, The Netherlands, e-mail: c.r.kleijn@tudelft.nl

Lecture Notes in Computational Science and Engineering 71,

DOI 10.1007/978-3-642-03344-5_3,

B. Koren and C. Vuik (eds.), Advanced Computational Methods in Science and Engineering,

S. van Veldhuizen, C. Vuik, and C.R. Kleijn

to reduce the computational time of the time accurate simulation of the classical 17

species, 26 reactions chemistry model by a factor 20 on a single processor.

1 Introduction

Chemical Vapor Deposition (CVD) is a chemical process which transforms gaseous

molecules into high-purity, high-performance solid materials in the form of, for in-

stance, a thin ﬁlm or a powder. The production of thin ﬁlms via CVD is of consid-

erable importance for the micro-electronics industry, but also in other technological

areas applications of thin solid ﬁlms via CVD can be found. For instance, in the

glass industry protective and decorative layers may be deposited on glass via CVD.

In a typical CVD process the material to be deposited is introduced into the reactor

chamber in one or more gas(es), called precursors, which react and/or decompose

on the substrate surface to produce the desired deposit. The volatile byproducts are

removed by the gas ﬂow through the reactor.

Numerical simulations are a widely used tool to design CVD reactors and to

optimize the process itself [16]. In most cases, these are steady state simulations,

since the total process time is large compared to the transients during start-up and

shut-down. However, with the deposited ﬁlms getting thinner and thinner, process

times are reduced and transient times become of more importance. Also for the study

of inherently transient CVD processes, such as Rapid Thermal CVD (RTCVD) and

Atomic Layer Deposition (ALD), transient simulations are indispensable.

The aim of this study is to develop nonstationary solvers for CVD processes.

The numerical modeling of realistic CVD processes based on detailed chemistry, in-

volves the solution of multi-dimensional advection-diffusion-reaction equations for

a large number of reactants and intermediate species. These equations are nonlin-

early and stifﬂy coupled through the reaction terms, which typically include dozens

of elementary ﬁnite rate reactions with largely varying rate constants. It is difﬁcult

to ﬁnd the solution of such stiff systems, especially in the case one wants to ﬁnd a

time-accurate transient solution.

The numerical solvers present in most commercial CFD codes have great prob-

lems producing time-accurate, transient (and even steady state) results for laminar

reacting ﬂow simulations such as CVD. Although some commercial CFD codes

claim to be able to handle stiff chemistry, no successful attempts to model multi-

dimensional gas-ﬂow with multi-species, multi-reaction CVD chemistry using com-

mercial CFD codes have been reported in literature.

Alternative solution methods developed in the computational physics communi-

ties include ideas as the following. A ﬁrst approximation would be to integrate the

advection and diffusion terms explicitly, and the reaction terms implicitly. Then, per

grid point the solution of a nonlinear systems of the size of the number of reac-

tive species is needed. This could easily be done by means of a Newton method. A

fully coupled approach, called the IMEX Runge-Kutta Chebyshev method, is dis-

cussed in Section 4.2. When using this approach, then it is important to integrate

On Numerical Issues in Time Accurate Laminar Reacting Gas Flow Solvers

the discretized diffusion part stably, which is certainly not a straightforward task

to accomplish. Secondly, one could also march through the grid from grid point to

grid point and solve the nonlinear system of reaction terms. This strategy looks like

a nonlinear Gauss-Seidel method and is used by Kleijn, see [15].

For strongly diluted laminar reacting ﬂow problems, in which the ﬂow and tem-

peratures are not inﬂuenced by the reactions, the computation of the ﬂow and tem-

perature ﬁeld is rather trivial in comparison with the solution of the system of

advection-diffusion-reaction equations. Therefore, we mainly focus on efﬁcient so-

lution techniques for the stiff set of advection-diffusion-reaction equations. Besides

stability requirements for stable integration in time, preservation of non-negativity

of the species concentrations is required as well. In [24] we discussed this so-called

positivity property, which puts severe restrictions on the time step size. In Section 4

we present further details on stability and positivity conditions for time integration

methods.

It appears that the ﬁrst order Euler Backward method is both unconditionally sta-

ble and unconditionally positive. Because of these properties, we restrict ourselves

to the Euler Backward method for time integration. The species concentrations re-

main positive within Newton’s method, used to solve the nonlinear systems within

Euler Backward, when a direct solver is used to obtain the solution of the linear sys-

tems. However, when iterative linear solvers are used, the solutions of the nonlinear

systems may have small negative components, despite the unconditional positivity

of Euler Backward. In order to prevent this, we introduce a projected version of

Newton’s method. Further details are discussed in Section 5.1.

The linear systems which have to be solved in the Euler Backward method, are

sparse and large. Preconditioned Krylov solvers are suitable to reduce computa-

tional costs. In Section 5.2 we report on the comparison of various preconditioners

and their relationship to the positivity of the solution. We conclude with a descrip-

tion of the chemistry models in the test problems, and discuss the numerical results

obtained. We want to emphasize that all results presented in this paper have been

presented in previous work. To summarize, References [22, 24] are summarized in

Section 4, whereas the the discussion on the simulation results can also be found in

[21].

Finally, we remark that the computational methods presented in this paper are

not only applicable in CVD, but also in applications such as laminar combustion

[8] and Solid Oxide Fuel Cell modeling [27]. Under the restriction that the spatial

discretization is structured, we conjecture that our methodology is also applicable

in these applications.

2 Numerical modeling of chemical vapor deposition

Thin solid ﬁlms are widely used in many technological areas such as micro-

electronics and the glass industry, with applications varying from insulating and

(semi-)conducting layers in the micro-electronics, to optical, mechanical and/or dec-

S. van Veldhuizen, C. Vuik, and C.R. Kleijn

orative coatings on glass. The production of such thin layers can be done by various

deposition processes, e.g. sputtering, evaporation and CVD. Involving chemical re-

actions clearly distinguishes CVD from the other production technologies, whereby

the most important advantage is its capability of depositing ﬁlms of uniform thick-

ness on highly irregularly shaped surfaces [11].

Basically, a CVD system is a chemical reactor in which precursor gases contain-

ing the atoms to be deposited are introduced, usually diluted in an inert carrier gas.

Furthermore, the reactor chamber contains substrates on which the deposition takes

place. In this study it is assumed that the energy to drive the (gas phase and surface)

reactions is thermal energy.

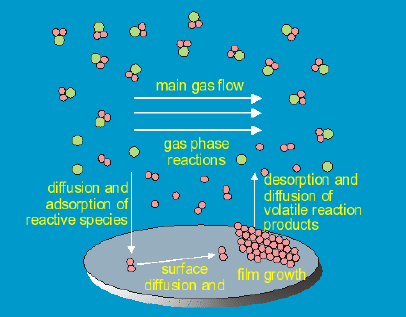
Basically, the following six steps occurring in every CVD process have to be

mathematically modeled:

1. Convective and diffusive transport of reactants from the reactor inlet to the reac-

tion zone within the reactor chamber

2. Chemical reactions in the gas phase leading to a multitude of new reactive species

and byproducts,

3. Diffusive transport of the initial reactants and the reaction products from the

homogeneous reactions to the susceptor surface, where they are adsorbed on the

susceptor surface,

4. Surface diffusion of adsorbed species over the surface and heterogeneous surface

reactions catalyzed by the surface, leading to the formation of a solid ﬁlm,

5. Desorption of gaseous reaction products, and their diffusive transport away from

the surface,

6. Convective and/or diffusive transport of reaction products away from the reaction

zone to the outlet of the reactor.

For fully heterogeneous CVD processes the second step in the above enumeration

does not take place. Steps one to six are illustrated in Figure 1

Fig. 1 Schematic represen-

tation of the six basic steps

in CVD. This illustration is

taken from [13].

On Numerical Issues in Time Accurate Laminar Reacting Gas Flow Solvers

2.1 Transport model for the gas species

To mathematically model a CVD process, the gas ﬂow, the transport of thermal

energy, the transport of species and the chemical reactions in the reactor have to be

described. We assume that the gas mixture in the reactor behaves as a continuum, as

an ideal gas and in accordance with Newton’s law of viscosity. The gas ﬂow in the

reactor is assumed to be laminar.

The composition of the N component gas mixture is described in terms of the

dimensionless mass fractions

, which sum up to one. Transport of total mass, mo-

mentum and heat are described respectively by the continuity equation, the Navier-

Stokes equations and the transport equation for thermal energy. Note that the con-

sumption and production of heat due to the chemical reactions is also included in the

energy equation. For most CVD systems, especially when the reactants are highly

diluted in an inert carrier gas, the heat of reactions has a negligible inﬂuence on

the gas temperature distribution. For such systems, the computation of the laminar

ﬂow and the temperature ﬁeld is a relatively trivial task, which can be performed

preceding to and independently of the calculation of the species concentrations. The

difﬁculty, however, lies in solving the set of highly nonlinear and strongly coupled

species equations.

Transport of mass fraction

is described by the i-th species equation

∂

(

ρω

)

∂

= −∇·(

) + ∇·[(

∇

) + (D

∇(lnT ))] + m

∑

k=1

, (1)

where diffusive mass ﬂuxes are due to concentration diffusion and thermal diffusion.

In (1) D

is the effective ordinary diffusion coefﬁcient and D

is the effective thermal

diffusion coefﬁcient for species i [15], v the mass averaged velocity obtained from

the Navier-Stokes equations, and

the density of the gas mixture. Suppose that K

reversible gas-phase reactions of the form

∑

i=1

′

k,forward

⇄

k,backward

∑

i=1

′′

(2)

take place. The net molar reaction rate R

for the k

reaction in the last term on the

right-hand side of (1) is computed as

= k

k,forward

∏

i=1



RTm



′

−k

k,backward

∏

i=1



RTm



′′

. (3)

In eq. (2), A

are the species in the gas mixture,

′

the forward stoichiometric

coefﬁcient for species i in reaction k,

′′

the backward stoichiometric coefﬁcient

for species i in reaction k. The net stoichiometric coefﬁcient

is then deﬁned as

′′

−

′

. In eq. (3), P is the pressure in Pa, T the temperature, R the universal

gas constant, m

the molar mass of species i and m the average molar mass, computed

S. van Veldhuizen, C. Vuik, and C.R. Kleijn

m =



∑

i=1



. (4)

Usually, the forward reaction rate constant k

k,forward

is ﬁtted according to a modiﬁed

Arrhenius expression:

k,forward

(T) = A

−E

, (5)

where A

and E

are ﬁt parameters. For the CVD process considered in the

present paper, these ﬁt parameters are available through the references presented

in Section 3. The backward reaction rate constants k

k,backward

are computed self-

consistently from the forward reaction rate constants and reaction thermo-chemistry,

see [14]. The time constants of the fastest and slowest reactions can differ many (e.g.

25) orders of magnitude, introducing stiffness into the species equations (1). For a

detailed description of the mathematical model for CVD, and the corresponding

boundary conditions, we refer to [14, 15] and to Section 3.

2.2 Modeling of surface chemistry

We assume that at the wafer surface S irreversible surface reaction takes place. The

s-th transformation of gaseous reactants into solid and gaseous reaction products is

of the form

∑

i=1

′

−→

∑

i=1

′′

∑

j=1

′′

, (6)

with A

as before, B

the solid reaction products, M the number of solid reaction

products,

′

and

′′

are the stoichiometric coefﬁcients for gaseous species i in sur-

face reaction s and

the stoichiometric coefﬁcient for the solid species. Again, the

net stoichiometric coefﬁcient

is deﬁned as

′′

−

′

Usually, heterogeneous surface reactions are characterized by complicated re-

action mechanisms that consist of a number of steps. The surface reaction rate R

will therefore depend on the partial pressures of gaseous species, the rate constants

of the individual steps (as functions of local temperature), temperature and other

surface properties. However, there is in general little or no information available on

the individual reaction steps and rate constants. The most common way to model the

surface reaction is to propose a mechanism and assume that one of the reaction steps

is rate limiting, whereas all other reaction steps are in equilibrium. In this study we

are not interested in the qualitative modeling of surface chemistry; we will make use

of surface reaction mechanisms for which the surface reaction rates are known. For

further details on surface reaction modeling we refer to [14].

If the surface reaction rate R

can be computed, then the growth rate G

in nm/s

of solid species j is deﬁned as