Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

quasiclassical parameter (p

)

to the terms which are already present in eqn

(10.41); it thus should be neglected.

Equation (10.41) can be further modified using the equation for the static Green

functions

(10.46)

The non-quasiclassical correction can be omitted here. Multiplying this equation

by f

and subtracting it from eqn (10.41), we obtain

(10.47)

where

(10.48)

and

(10.49)

In the literature, the function is used sometimes instead of the function f

, it

is defined according to

(10.50)

where is the phase of the order parameter. Using the fact that the collision

integral

vanishes for any function independent of the momentum-direction

[see eqn (10.76)] we find instead of eqns (10.47)

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [196]-[200]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共7页 2010-8-8 15:55

end p.196

(10.51)

where the operator acts only on the modulus of the order parameter.

Equation (10.51) can be further transformed into

(10.52)

Equation (10.44) becomes

(10.53)

These are the equations for the new function .

10.2.2 Discussion

The kinetic equations eqn (10.41) [or eqn (10.47)], and eqn (10.44) for the

distribution functions f

and f

are the central result of this chapter. The kinetic

equations contain the momentum derivatives of

f/ p multiplied by “forces”

which include the Lorentz force f

= (e/c) [v

× H] and the forces arising due to

spatial variations of the order parameter. Note that the electric field is included

in the terms which describe the energy variation in time, since E is of the first

order in time-derivative. For this reason, it does not enter the force terms.

As we saw already on page 195, the function f

appears in the l.h.s. of eqn

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共7页 2010-8-8 15:55

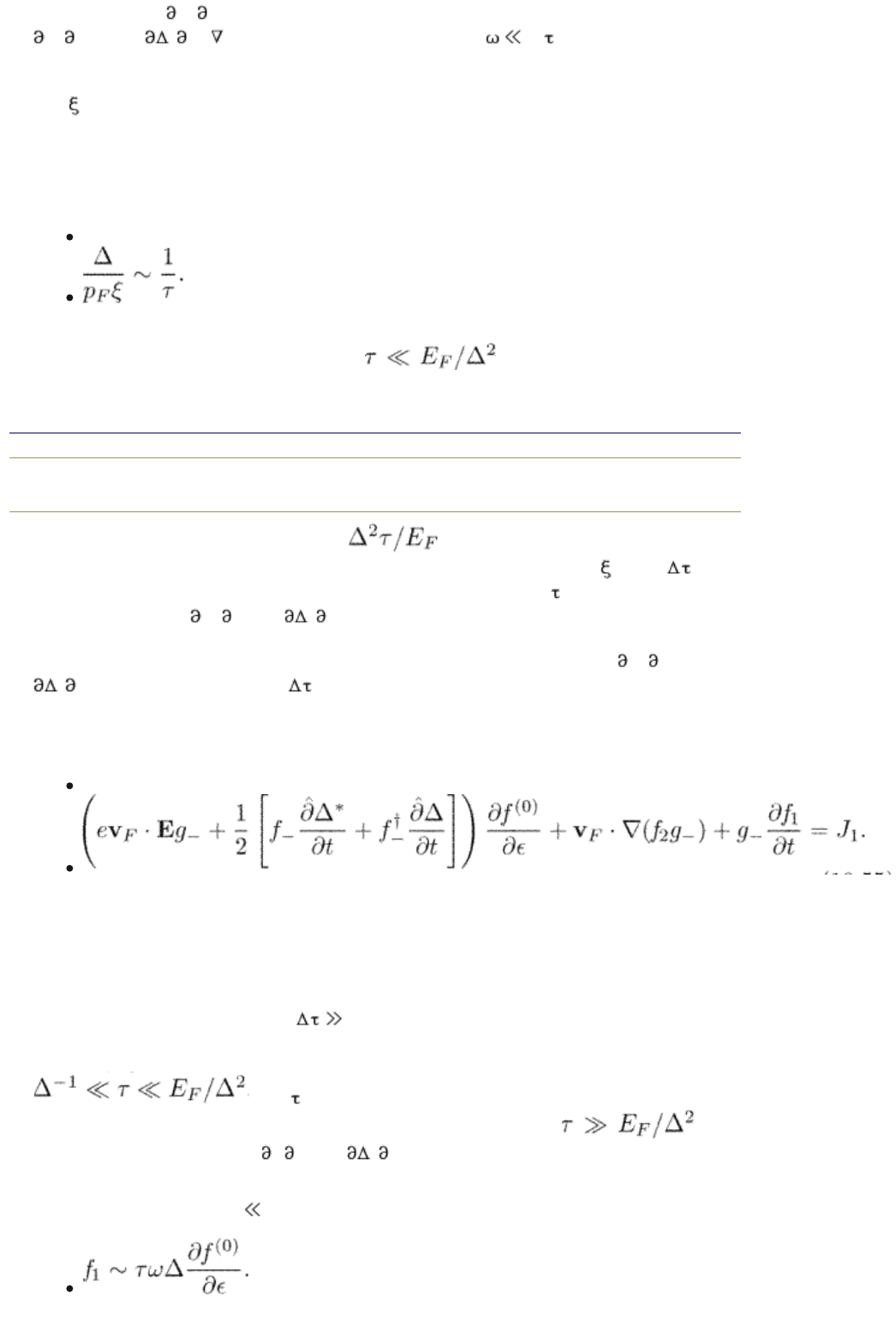
(10.41) only as f

/ t and in combinations with the momentum derivatives

/ p or as ( / p) f

. For a slow variation in time, 1/ , the only terms

with f

are those with the momentum derivatives of the distribution function and

of the order parameter. Such terms only exist in the first-order approximation in

1/p

. All other non-quasiclassical contributions are omitted: they turn out to be

corrections to the first line of eqn (10.41) which already exists in the zero

approximation.

From eqn (10.41) we note that the momentum derivatives are of the same order

of magnitude as the collision integrals when

(10.54)

The relative importance of the terms with the momentum derivatives decreases

as the mean free path gets shorter. For

, their contribution to

the

end p.197

distribution function is of the order of as compared to that determined

by the collision integral. This correction becomes of the order of 1/p

when

decreases down to values of the order of unity. For such short , the

contributions from f

/ p and / p become comparable or less than the terms

which we have neglected during the derivation of the quasiclassieal kinetic

equations. Thus, it becomes illegal to keep the momentum derivatives

/ p and

/ p in equation (10.41) for ~ 1 and they should be neglected. Therefore,

for dirty superconductors, eqns (10.41, 10.44) should be used with the

momentum derivatives neglected. In the dirty case we thus obtain from eqn

(10.41)

(10.55)

Equation (10.44) can be used as it stands. These equations can be also obtained

directly from the Eliashberg equations (9.2) using the Keldysh function, in the

form of eqn (9.25) with the distribution, function, from eqn. (9.28). The

derivation of the quasiclassical set of equations (10.55) and (10.44) for dirty

superconductors is described in the review by Larkin and Ovchinnikov (1986).

For clean superconductors with

1, on the contrary, the momentum

derivatives should be included into the kinetic equations. They give small

contributions in the so-called moderately clean, regime when

. As increases further, their role becomes more

important. Finally, in the collisionless limit (superclean regime)

the momentum derivatives

f/ p and / p dominate.

One more observation is that, for clean superconductors interacting with

electromagnetic fields, f

. Indeed, eqn (10.41) gives

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共7页 2010-8-8 15:55

On the other hand, eqn (10.44) shows that the variation of f

is f

~ f

(0)

along a trajectory part with a length of the order of . This variation is much

smaller than f

itself. Therefore, eqn (10.44) reduces simply to

(10.56)

i.e., the function f

is constant along the quasiparticle trajectory. As a result, eqn

(10.41) implies that f

~ f

(0)

/ , i.e., f

. It is this condition that allows

one to neglect non-quasiclassical corrections to f

and to use eqn (10.56) in a

clean superconductor.

Equation (10.56) holds for a trajectory which is not very long. The maximum

length L is determined by the shortest of the three length scales: L

min { ,

/ ) , r

} where is the characteristic scale of variations of the order

parameter, and r

is the Larmor radius. If this condition is violated, one

cannot neglect the other terms in eqn (10.39) any more. This condition,

end p.198

in particular, determines the necessary requirement of validity of eqn (10.56); it

is L

which is equivalent, of course to the clean-limit condition .

The non-quasiclassical corrections to eqn (10.44) which were omitted during the

derivation may become important for problems associated with the heat

transport, when there exists a temperature gradient in a superclean regime with

and longer. In this case, on the contrary, the function f

is larger

than f

and eqn (10.41) gives g f

= const. The second equation (10.44) should

then be derived including the non-quasiclassical corrections. We shall not

consider such problems here.

10.3 Observables In the gauge-invariant representation

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共7页 2010-8-8 15:55

Using the modified gauge-invariant Green functions, the current can be written

(10.57)

Here for and for according to

the definition of the gauge-invariant functions. We see that the diamagnetic term

does not appear explicitly for the gauge-invariant representation in the

quasiclassical limit. Performing shifts in the momentum under the integrals we

can write the current through the gauge-invariant quasiclassical Keldysh

functions in the usual form

(10.58)

The order parameter is

(10.59)

where | g | is the pairing interaction. The quasiclassical version of this expression

(10.60)

where = (0) | g | is the pairing constant.

The electron density is (Eliashberg 1971)

in terms of the usual Green functions. The scalar potential appears in the r.h.s.

due to a change in the normal-state density caused by a e

variation of the

chemical potential. The electron density becomes

end p.199

(10.61)

in terms of the gauge-invariant Green functions. Here we use that

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共7页 2010-8-8 15:55

and

The latter follows from the observation that for | |

We can now replace the gauge-invariant functions in equations (10.58), (10.60),

and (10.61) with the usual (gauge-covariant) functions. The only condition is

that they have to be determined by the gauge-invariant kinetic equations

(10.41) and (10.44) together with the gauge-invariant parameterization for the

Keldysh function through f

and f

The Keldysh function takes the form

where . We shall neglect, the small non-quasiclassical

corrections and write

(10.62)

In this approximation, the Keldysh function is parametrized by two distribution

functions f

and f

With eqn (10.62), the current and the order parameter have their usual form

(10.63)

and

(10.64)

The expressions for the internal energy and the internal energy current can also

be written in terms of the gauge-invariant functions. We have

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共7页 2010-8-8 15:55

end p.200

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第7页共7页 2010-8-8 15:55

In the quasiclassical representation, it becomes

(10.65)

Here

is the energy in the normal state, and g is the deviation of the Green

function from the normal state. We have separated the normal state contribution

because the normal state energy cannot be calculated within the quasiclassical

approximation: the momentum integral is determined by

far from the Fermi

surface. The energy current takes the form

(10.66)

10.3.1 The electron density and charge neutrality

The electron density eqn (10.61) takes the form

The combination is nonzero in a

nonstationary situation. To find it, we use the normalization condition

We put where is the stationary Green function and is

a nonstationary correction and find

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [201]-[205]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共7页 2010-8-8 15:56

We multiply this equation by and take the trace

With help of the identity g

f f =1 we obtain

end p.201

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共7页 2010-8-8 15:56

(10.67)

and the same for the advanced function. Next, we note that according to the

particle–hole symmetry of the Eilenberger equations (5.89)–(5.91), the static

Green functions transform as

(10.68)

under the transformation , p p. Therefore, the first line of eqn

(10.67) transforms into

while the second line transforms into

As a result, we can write

where A ( , p) is an even function of ( , p) while the first term is an odd function

of these variables. The term with A ( , p) vanishes after integration with the odd

function f

(0)

= tanh ( /2T). The electron density becomes

(10.69)

where is defined by eqn (10.4), and the averaging over momentum directions

eqn (5.72) is implied. Integrating by parts in the first line and using that

we find

(10.70)

With the definition equation (10.50) of the function , the electron density can

be written as

(10.71)

In metals, all bulk charges are screened. It can be seen from the Poisson

equation for the normal state

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共7页 2010-8-8 15:56