Контрольная работа - Индуктивная и описательная статистика
Подождите немного. Документ загружается.

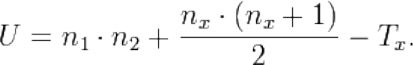
присвоенных при совместном ранжировании. Подсчитываем отдельно сумму
рангов, пришедшихся на долю элементов первой выборки, и отдельно — на
долю элементов второй выборки — Таблица №5.
Так как в ранжируемой объединенной выборке есть совпадающие ранги,
то необходимо проверить правильность ранжирования:
Общая сумма рангов = 372,5 + 447,5 = 820
Расчетная сумма рангов: ΣR
i
= (n•(n+1))/2 = (40•(40 + 1)/2 = 820
Равенство реальной и расчетной сумм рангов соблюдено.
3) Определяем значение U
эмп
— эмпирическую величину критерия
Манна-Уитни по формуле:
где n
1
― количество испытуемых в первой выборке;
n
2
― количество испытуемых во второй выборке;
T
x
― большая из двух ранговых сумм;
n
x
― количество испытуемых в выборке с большой суммой рангов.
Из таблицы №4 видно, что большей из двух ранговых сумм оказывается
сумма рангов у выборки мужчин, обратившихся в службу знакомств — 447,5.
U
эмп-муж
= (17 • 23) + ((17 • (17 + 1)) / 2) ― 447,5 = 391 + (306 / 2) ― 447,5 =
= 544 ― 447,5 = 96,5
Поскольку в нашем случае n
1
≠
n
2
, подсчитаем
U
эмп
и для второй
ранговой суммы — 372,5, подставляя в формулу соответствующее ей
значение — n
x
:
U
эмп-жен
= (17 • 23) + ((23 • (23 + 1))/2) ― 372,5 = 391 + (552/2) ― 372,5 =
= 667 ― 372,5 = 294,5
Так как меньшее значение критерия Манна-Уитни свидетельствует о
21

больших различиях, то в качестве эмпирического значения U–критерия
берется меньшее значение U
эмп
. В нашем случае мы принимаем за
U
эмп
=
U
эмп-муж
= 96,5 — значение U‒критерия для выборки мужчин, обратившихся
в службу знакомств, что подтверждает теоретические ожидания
исследователей о том, что мужчинам приходится преодолевать субъективно
более интенсивное внутренне сопротивление.
5) Определяем критические значения U
кр
по таблице критических
значений критерия Манна-Уитни для соответствующих n, причем меньшее
n принимаем за n
1
= 17, а большее n принимаем за n
2
= 23
n
1
,n
2
p
0,95 0,99
17,23 134 109
6) Построим «ось значимости»:
Так U–критерий Манна‒Уитни является исключением из общего правила
принятия решения о достоверности различий, то можно констатировать
достоверные различия, если U
эмп
≤ U
кр.
U
эмп
= 96,5
U
кр
= 109 (p = 0,99)
U
эмп
≤ U
кр
(p = 0,99) ⇒ Hₒ отклоняется, H
1
принимается с вероятностью
ошибки I рода α=1 – p = 0,01
22
Статистическое решение: Hₒ отклоняется. H
1
принимается с
вероятностью ошибки α=0,01. Мужчинам при обращении в службу
знакомств приходится преодолевать субъективно более интенсивное
внутренне сопротивление, чем женщинам.
Содержательный вывод: статистически достоверно, что при обращении в
службу знакомств мужчинам из исследованной выборки пришлось
преодолеть субъективно более интенсивное внутренне сопротивление, чем
женщинам.
23

Задание №4
По методике Тулуз-Пьерона исследовалось оперативное внимание у 10
детей в возрасте от 5 лет до 10 лет. Зависит ли скорость выполнения
корректурной пробы (среднее число просмотренных знаков за 10 минут) от
возраста (для соблюдения интервальности шкалы месяцы переведены в доли
года)?
Испытуемые Возраст Скорость V
1. Саша Д. 7,42 81,1
2. Дамир 7,83 84,5
3. Женя 5,67 25,9
4. Оля 6,75 46,9
5. Кирилл М. 5,83 44,8
6. Кирилл С. 6,17 39,9
7. Кирилл К. 6,25 40,8
8. Саша Ю. 7,17 44,1
9. Юля П. 10,08 71
10. Юля К. 6,83 30,4
24

Решение №1.4
1) Принятие решения о методе математической обработки.
Так как в нашем случае необходимо выявить наличие взаимосвязи между
двумя метрическими признаками, измеренными на одной выборке,
следовательно для данного исследования целесообразно использовать
коэффициент линейной корреляции Пирсона.
2) Коэффициент линейной корреляции Пирсона относится к группе
параметрических методов и поэтому его следует применять только тогда,
когда известно или доказано, что распределение результативного признака
является нормальным.
а) Для того, чтобы убедится в нормальности распределения
результативного признака (скорости выполнения корректурной пробы ― V
i
),
произведем необходимые расчеты (Таблица №6) показателей асимметрии и
эксцесса, и сопоставим их с критическими значениями (по Н.А.
Плохинскому):.
Таблица №6
i
V
i
V
i
– M
V
(V
i
– M
V
)
2
(V
i
– M
V
)
3
(V
i
– M
V
)
4
1 81,1 30,16 909,63 27434.31 827418,72
2 84,5 33,56 1126,27 37797,74 1268492,2
3 25,9 ─25,04 627 15700,12 393131
4 46,9 ─ 4,04 16,32 65,94 266,39
5 44,8 ─ 6,14 37,7 231,48 1421,26
6 39,9 ─ 11,04 121,88 1345,57 14855,12
7 40,8 ─ 10,14 102,82 1042,59 10467,61
8 44,1 ─ 6,84 46,79 320,01 2188,89
9 71 20,06 402,4 8072,22 161928,65
10 30,4 ─ 20,54 421,89 8665,65 177992,52
Σ
509,4
⇓
M
V
=
50,94
0
3812,7
⇓
D
v
= 318,27
100675,63 2858162
25
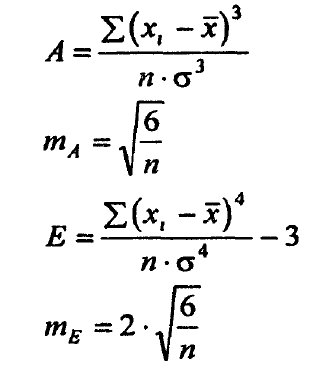
n = 10
M
V
= Σ V
i
/n = 509,4/10 = 50,94
D
v
= (Σ(V
i
– M
V
)
2
)/n = 3812,7/10 = 318,27
σ
v
= (D
v
)
½
= (318,27)
½
= 19,526
Показатели асимметрии (A) и эксцесса (E) с их ошибками
репрезентативности (m
A
,
m
E
) определяются по формулам:
В нашем случае:
A = (Σ(V
i
– M
V
)
3
)/n • σ
v
3
= 100675,63/(10 • (19,526)
3
) =
= 100675,63/10 • 7444,574 = 100675,63/74445,74 = 1,352
m
A
= (6/n)
½
=
(6/10)
½
= (0,6)
½
= 0,7746
E = ((Σ(V
i
– M
V
)
4
)/n • σ
v
4
) – 3 = (2858162/(10 • (19,526)
4
)) – 3 =
= (2858162/1453627,4) – 3 = 1,966 – 3 = – 1,034
m
E
= 2 • (6/n)
½
=
2 • (6/10)
½
= 2 • (0,6)
½
= 2 • 0,7746 = 1,5492
б) Показатели асимметрии и эксцесса свидетельствуют о достоверности
отличия эмпирического распределения от нормального в том случае, если они
превышают по абсолютной величине свою ошибку репрезентативности в 3 и
более раза:
26

В нашем случае:
t
A
= |A|/m
A =
1,352/0,7746 = 1,745
t
E
= |E|/m
E =
1,034/1,5492 = 0,667
Так асимметрия и эксцесс не превышают в три раза свою ошибку
репрезентативности, то можно заключить, что распределение признака
(скорости выполнения корректурной пробы) не отличается от нормального.
в) Произведем проверку по формулам Е.И. Пустыльника: рассчитаем
критические значения для асимметрии и эксцесса.
A
кр
= 3 • (6 • 9/11 • 13)
½
= 3 • (54/143)
½
=
3 • (0,378)
½
=3 • 0,615 = 1,844
A
эмп
= 1,352
A
эмп
< A
кр
E
кр
= 5 • (24 • 10 • 8 • 7/11 • 11 • 13 • 15)
½
= 5 • (13440/23595)
½
=
= 5 • (0,5696)
½
= 5 • 0,755 = 3,774
E
эмп
= – 1,034
E
эмп
< E
кр
Оба варианта проверки по Н.А. Плохинскому и по Е.И. Пустыльнику,
дают один о тот же результат: распределение скорости выполнения
корректурной пробы в группе испытуемых детей не отличается от
27

нормального распределения, следовательно можно продолжать исследование
для определения взаимосвязи между двумя признаками с помощью
коэффициента линейной корреляции Пирсона.
3) Формулируем нулевую (Hₒ) и альтернативную (H
1
) гипотезы:
Hₒ : r
B,V
= 0
Корреляция между показателями возраста и скоростью выполнения
корректурной пробы значимо не отличается от нуля (является случайной).
H
1
: r
B,V
≠ 0
Корреляция между показателями возраста и скоростью выполнения
корректурной пробы значимо отличается от нуля (является не случайной).
4) Произведем необходимые расчеты для коэффициента линейной
корреляции, а полученные результаты занесем в Таблицу №7.
Таблица №7
i
Возраст
B
i
Скорость
выполн.
корретур.
пробы
V
i
B
i
–
M
B
(B
i
—
M
B
)
2
V
i
–
M
V
(V
i
–
M
V
)
2
(B
i
–
M
B
)•
(V
i
–
M
V
)
1 7,42 81,1 0,42 0,176 30,16 909,63 12,67
2 7,83 84,5 0,83 0,689 33,56 1126,27 27,85
3 5,67 25,9 ─ 1,33 1,769 ─25,04 627 33,3
4 6,75 46,9 ─ 0,25 0,063 ─ 4,04 16,32 1,01
5 5,83 44,8 ─ 1,17 1,369 ─ 6,14 37,7 7,18
6 6,17 39,9 ─ 0,83 0,689 ─ 11,04 121,88 9,16
7 6,25 40,8 ─ 0,75 0,563 ─ 10,14 102,82 7,61
8 7,17 44,1 0,17 0,029 ─ 6,84 46,79 ─ 1,16
9 10,08 71 3,08 9,486 20,06 402,4 61,78
10 6,83 30,4 ─ 0,17 0,029 ─ 20,54 421,89 3,49
Σ
70
⇓
M
B
= 7
509,4
⇓
M
V
=
50,94
0
14,862
0
3812,7 162,89
28
Опираясь на данные полученные в Таблице №7, рассчитаем стандартное
отклонение и ковариацию для двух переменных – B
i
и
V
i
D
B
= (Σ(B
i
– M
B
)
2
)/n =14,862 /10 = 1,486
σ
B
= (D
B
)
½
= (1,486)
½
= 1,219
D
v
= (Σ(V
i
– M
V
)
2
)/n = 3812,7/10 = 318,27
σ
v
= (D
v
)
½
= (318,27)
½
= 19,526
COV
B,V
= Σ(B
i
– M
B
)•(V
i
– M
V
)/n = 162,89/10 = 16,289
Подсчитаем значение коэффициента линейной корреляции Пирсона:
r
B,V
= COV
B,V
/ σ
B
•
σ
v
r
B,V
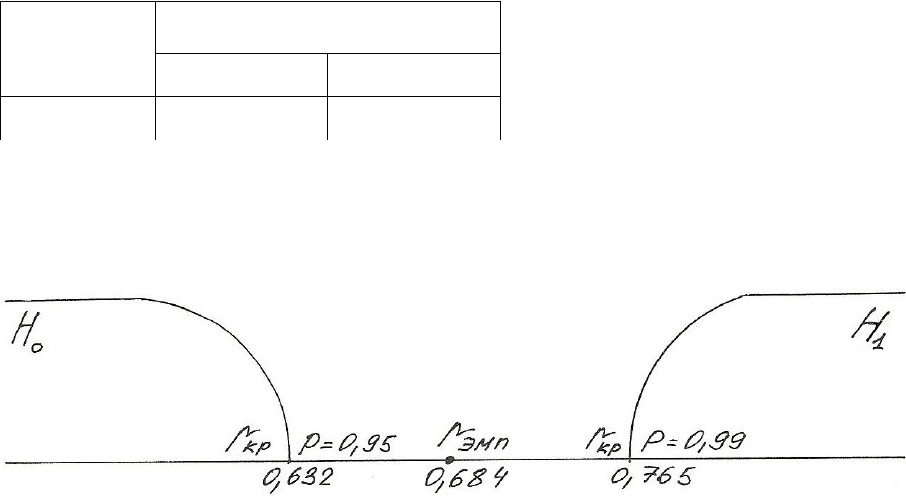
= 16,289 / 19,526 •1,219 = 16,289 /23,802 = 0,684
5) Проверяем на значимость полученный коэффициент корреляции r
B,V
с
помощью таблицы критических значений коэффициента линейной
корреляции Пирсона:
n
p
0,95 0,99
10 0,632 0,765
Для облегчения процесса принятия решения построим «ось значимости»:
Видно, что полученный коэффициент корреляции «попал в зону
неопределенности»: следовательно уже можно отклонить нулевую гипотезу,
но ещё нельзя принять альтернативную.
29
6) Продолжим проверку значимости полученного коэффициента
корреляции с помощью таблицы критических значений t−критерия
Стьюдента: .
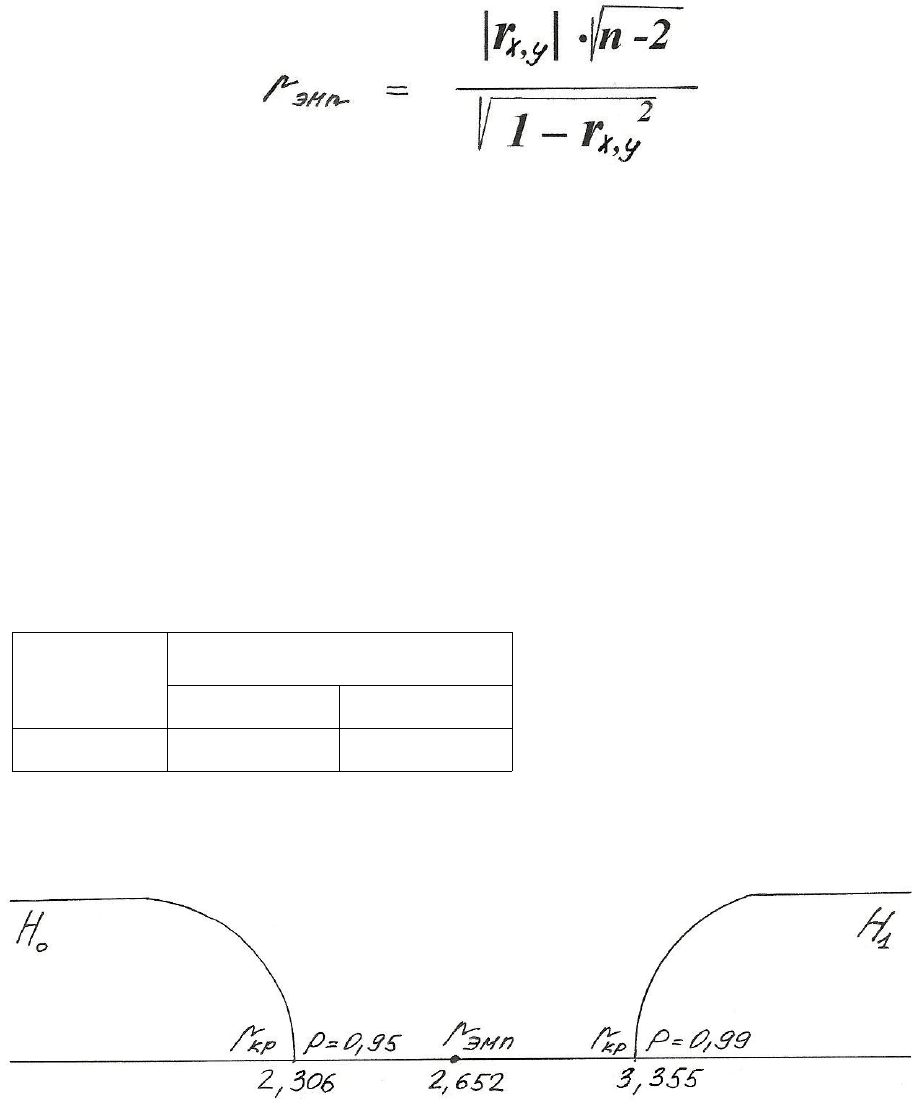
а) вычисляем эмпирическое значение r–критерия в ситуации проверки
гипотезы по формуле t−критерия Стьюдента:
r
эмп
= 2,652
б) вычисляем количество степеней свободы — ν:
ν = n – 2, где n – количество испытуемых выборке.
В нашем случае ν = 10 — 2 = 8
определяем критические значения r
кр
по таблице критических значений
t−критерия Стьюдента для ν = 8:
ν
p
0,95 0,99
8 2,306 3,355
Построим «ось значимости»:
30
