Коломитцев А.Д., Чернікова Л.В. Теорія автоматичного керування. Конспект лекцій
Подождите немного. Документ загружается.


0
n
a
и
0
1
n
.
Первое условие соответствует апериодической границе устойчивости, второе –
колебательной.
Рассмотрим частные случаи критериев устойчивости для систем первого,
второго и более высоких порядков.
Уравнение первого порядка а
0
р+а
1
=0;
0
0
a
;
0
11
a
. p
Единственный корень
0
1
1
a
a
p
будет отрицательным, если при а
0
>0
выполняется условие а
1
>0. Т.е. для системы первого порядка достаточно выполнение
необходимого условия устойчивости.
Уравнение второго порядка а
0
р
2
+а
1
р+а
2
=0.
Имеет главный определитель:
20
1
0
aa
a
.
В соответствии с критерием Гурвица необходимо выполнение трех условий:
.0
;0
;0
212
11
0
a
a
a
Третье условие выполняется при положительном а
2
>0. Т.е. и для системы
второго порядка необходимое условие устойчивости является и достаточным.
Апериодической границе устойчивости соответствует условие а
2
=0, а колебательной
– а
1
=0.
Уравнение третьего порядка а
о
р
3
+а
1
р
2
+а
2
р+а
3
= 0.
Имеет главный определитель:
31
20
31
3
0
0
0
aa
aa
aa
Для этого уравнения имеем четыре условия:
74

0
0
a
;
0
11
a
;
0
0321
20
31
2
aaaa
aa
aa
; (3.8)
0
323
a
.
Четвертое условие сводится к условию
0
3
a
. Условие
0
2
a
при
0
0
a
;
0
1
a
и
0
3
a
может выполняться только при
0
2
a
. Но, кроме того, должно
выполняться уравнение четвертого порядка а
о
р
4
+а
1
р
3
+а
2
р
2
+а
3
р+а
4
= 0. Имеет
главный определитель:
420
31
420
31
3
0
00
0
00
aaa
aa
aaa
aa
.
Условия устойчивости:
0
0
a
;
0
11
a
;
0
03212
aaaa
;
1
20
3
40
3
31
42
1
31
420
31
3
0
0
0
0
0
a
aa
a
aa
a
aa
aa
a
aa
aaa
aa
0)(
2
3041321
aaaaaaa
;
.0
434
a
Кроме положительности всех коэффициентов необходимо выполнение условий
.00)(
0321
2
3041321
aaaaиaaaaaaa
Для уравнения пятого порядка появляются еще дополнительные условия
устойчивости, кроме положительности коэффициентов.
Как видно, уже для уравнений выше четвертой степени условия устойчивости по
критерию Гурвица получаются громоздкими. Поэтому он используется для анализа
уравнений четвертого порядка.
75
Недостатком алгебраических критериев (в т.ч. и критерия Гурвица) является то,
что в случае неустойчивости АСУ они не дают ответа на вопрос, как надо изменить
параметры системы, чтобы она стала устойчивой.
3.3 Критерий устойчивости Михайлова
[1,c.139-143; 2,c.95-102; 3,c.141-144; 4,c.131-137; 5,c.149-153]
Сформулирован А.В. Михайловым в 1936 г.
Возьмем характеристический многочлен линейной системы n-го порядка:
nn
nn
apapapapD
1
1
10
...)(
. (3.9)
Подставим в этот полином чисто мнимое значение р=j
и получим
характеристический комплекс:
),()()(
jYXjD
где вещественная часть
)(
X
будет содержать четные степени параметра
:
...,)(
4
4
2
2
nnn
aaaX
(3.10)
а мнимая часть
)(
Y
- нечетные:
...,)(
5
5
3
31
nnn
aaaY
(3.11)
Комплекс
)(
jD
изобразится на комплексной плоскости в виде вектора с
проекциями на вещественную и мнимую оси соответственно
)()(
YиX
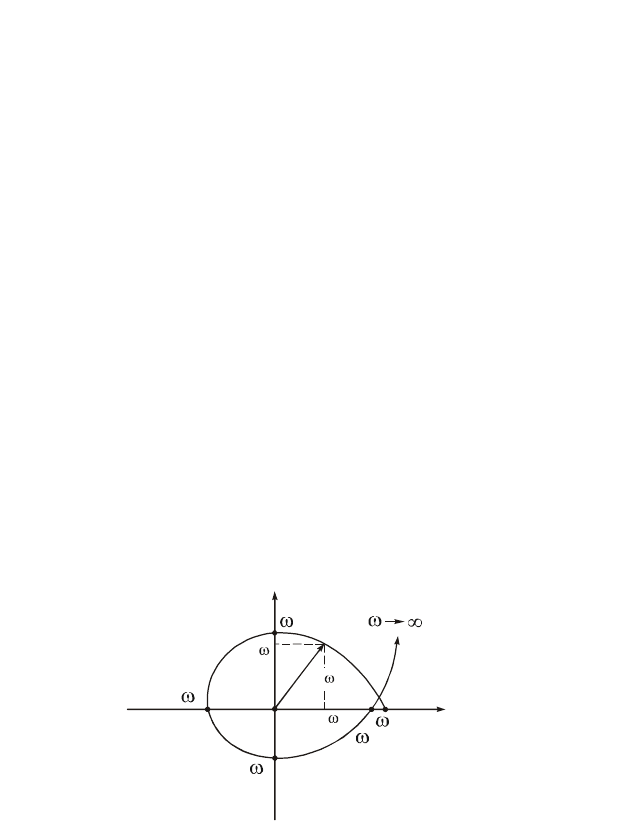
(рис. 3.3).
Если значения
менять непрерывно от 0 до
, то вектор
)(
jD
своим
концом опишет кривую (годограф), которая называется кривой Михайлова.
Практически кривая Михайлова строится по точкам. Задаются различными
значениями
и по (3.10) и (3.11) вычисляются
)(
X
и
)(
Y
.
Y
X
2
3
4
5
1
= 0
Y ( )
X ( )
0
D ( j )
76

Рисунок 3.3 – Изображение кривой Михайлова на
комплексной плоскости
Для устойчивости системы n-го порядка необходимо и достаточно, чтобы вектор
)(
jD
, описывающий кривую Михайлова, при изменении параметра
от 0 до
имел угол поворота
2
n
против часовой стрелки.
Для доказательства представим полином (3.9) в виде произведения
сомножителей:
),)...()(()(
210 n
ppppppapD
где
n
ppp ,...,
21
- корни характеристического уравнения.
Тогда характеристический комплекс примет вид:
))...()(()(
210 n
pjpjpjajD
. (3.12)
Т.е.
)(
jD
является произведением n комплексных чисел
n
nnn
j
n
jj
p
arctgpAeAeAeA
n
,,...,,
2
22
21
21
,
аргументы которых
),...,,(
21 n
при перемножении складываются. Поэтому
результирующий угол поворота вектора
)(
jD
будет равен сумме углов поворота
отдельных сомножителей (3.12) при изменении
от 0 до
:
n
...
21
. (3.13)
Пусть корень вещественный
11
p
. Тогда аргумент сомножителя
)(
1
pj
равен
)./()(
11
arctg
При изменении
от 0 до
результирующий угол поворота
2
1
при
0
1
и
2
1
при
0
1
.
Пусть два корня
2
p
и
3
p
- комплексные сопряженные
jp
3,2
.
Тогда аргумент пары сомножителей
jjjj
равен
77
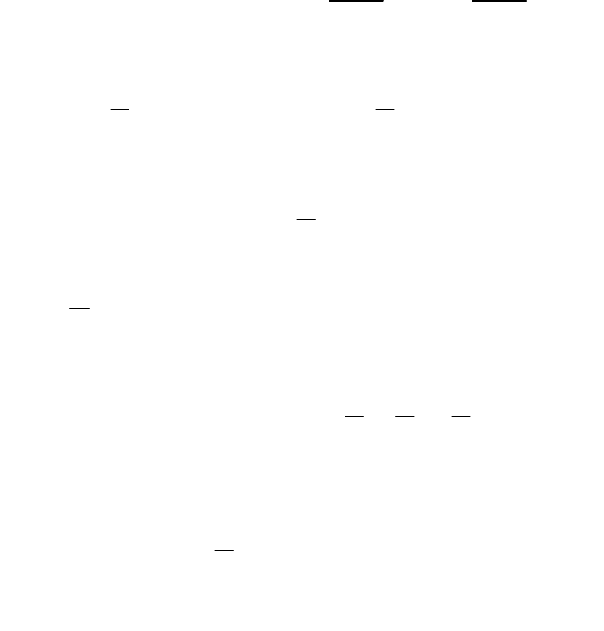
arctgarctg
23
.
При изменении
от 0 до
результирующий угол поворота
2
2
23
при
0
и
2
2
23
при
0
.
Если характеристическое уравнение будет иметь l корней вещественных или
комплексных с положительной вещественной частью, то им будет соответствовать
сумма углов поворотов, равная
2
l
. Остальным (n-l) корням с отрицательной
вещественной частью, будет соответствовать сумма углов поворотов, равная
2
)(
ln
. Общий угол поворота вектора
)(
jD
при изменении
от 0 до
согласно (3.13):
lnlln
222
)(
. (3.14)
Согласно требованию устойчивости необходимо и достаточно, чтобы все корни
имели отрицательные вещественные части
)0( l
. Поэтому в устойчивой системе
на основании (3.14)
2
n
.
Для устойчивой системы кривая Михайлова всегда имеет плавную
спиралевидную форму, конец которой уходит в
в квадранте, номер которого
равен степени n характеристического уравнения (рис. 3.4). Это позволяет
сформулировать критерий Михайлова в следующем виде. Для устойчивости
автоматической системы необходимо, чтобы кривая Михайлова проходила
последовательно столько квадрантов, какова степень n характеристического
уравнения, окружая начало координат против хода часовой стрелки.
78
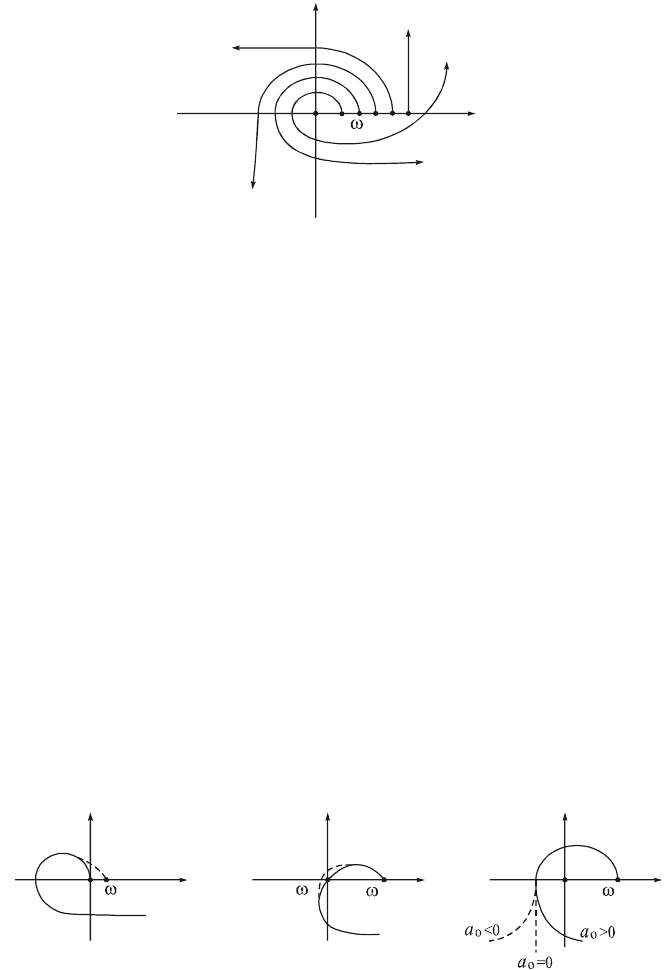
Рисунок 3.4 – Виды кривых Михайлова для устойчивых систем n-го порядка
При этом корни уравнений
0)(
X
и
0)(
Y
должны чередоваться.
Так как кривая Михайлова всегда начинается с точки
0
1
, расположенной на
вещественной оси, где мнимая часть обращатся в нуль
0)0()(
1
YY
, то при
увеличении
от 0 до
должна обращаться в нуль вещественная часть
0)(
2
X
, затем мнимая
0)(
3
Y
, затем опять вещественная
0)(
4
X
и т.д., причем
4321
0
. Поэтому для исследования устойчивости
системы достаточно определить ее качественный вид по токам пересечения с осями
координат.
При четной n кривая
параллельно оси Х, а при нечетной - параллельно
оси У ( всегда в n-ом квадранте).
По кривой Михайлова может быть определено наличие границ устойчивости
(рис.p3.5).
При апереодической границе устойчивости (нулевом корне)
0
n
a
, и кривая
Михайлова идет из начала координат (рис. 3.5, а). При колебательной границе
устойчивости D(р) обращается в нуль при подстановке
0
jр
:
0)()()(
ooo
jYXjD
.
а) б) в)
Y
X
= 0
0
n = 1
n = 2
n = 3
n = 4
n = 5
= 0
= 0 = 0
n = 4
n = 4
Y Y Y
X X X
o
0
0
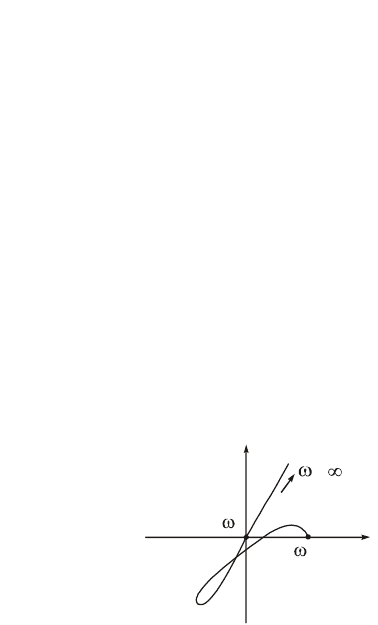
Рисунок 3.5 – Виды кривых Михайлова при прохождении
системы на границах устойчивости
Отсюда вытекает два равенства :
.0)(
;0)(
o
o
Y
X
(3.15)
Это значит, что точка
o
на кривой попадает в начало координат
(рис.p3.5,pб). При этом
o
есть частота незатухающих колебаний системы.
Для границы устойчивости третьего типа (бесконечный корень) конец кривой
перебрасывается в другую сторону. При этом
o
a
будет проходить через нулевые
значения, меняя знак плюс на минус (рис. 3.5, в).
Важно отметить следующее. На границе устойчивости системы все остальные
корни характеристического уравнения должны иметь отрицательные вещественные
части. Поэтому, кроме условия (3.15), требуется, чтобы кривая проходила бы все
остальные квадранты, кроме пропущенного из-за прохождения через начало
координат (как показано на рисунках 3.5, а и б). Если же кривая имеет вид,
показанный на рис.p3.6, то система находится не на границе устойчивости, а является
неустойчивой. Т.е. очертания кривой Михайлова на границе устойчивости должно
быть таким, чтобы после малой деформации ее в начале координат (случаи а и б) и
при малом
0
o
a
(случай в) можно было удовлетворить критерию устойчивости.
Рисунок 3.6 – Пример кривой Михайлова неустойчивой системы
3.4 Определение границ устойчивости [4,c.137-141]
При расчетах и проектировании АСУ необходимо бывает исследовать влияние
ее параметров на устойчивость. Для этого строят область устойчивости, т.е.
определяют области значений параметров, при которых система оказывается
устойчивой.
Y
X
o
= 0
=
79

Рассмотрим построение области устойчивости в плоскости двух параметров А и
В (это могут быть, например, коэффициент усиления и постоянная времени). Для
построения таких областей необходимо нанести линии, соответствующие границе
устойчивости. Область, ограниченная этими линиями, и будет областью
устойчивости.
Для построения границ устойчивости используются три признака существующих
типов границ устойчивости:
апериодической устойчивости
0
n
a
;
третьего типа устойчивости
0
o
a
;
для получения условия колебательной границы устойчивости у систем не выше
четвертого порядка может применяться критерий Гурвица. При этом
0
1
n
. Для
систем более высокого порядка удобнее пользоваться критерием Михайлова, в
соответствии с которым
0
o
jD
, т.е. прохождение кривой Михайлова через
начало координат.
Если интересующие нас два параметра А и В входят линейно в
характеристический комплекс, то для границ устойчивости колебательного типа
уравнение
0,, BAjD
o
распадается на два:
0,,
0,,
BAY
BAX
o
o
(3.16)
где
o
дает значение чисто мнимого корня, т.е. частоту гармонических
колебаний системы.
Выражение (3.16) является параметрическим уравнением границы устойчивости
при соблюдении дополнительного условия отрицательности вещественных частей
всех остальных корней. Это уравнение изображается в виде некоторых кривых на
плоскости параметров А и В. Задаваясь разными значениями
0
из
уравнений (3.16) определяют значения параметров А и В, и по полученным точкам
строятся границы устойчивости на плоскости А и В.
Для упрощения выделения границ области устойчивости вводится штриховка
полученных кривых. При перемещении вдоль кривой в сторону увеличения
надо
штриховать ее с левой стороны, если будет положительным определитель,
составленный из частных производных (3.16):
B
Y
A
Y
B
X
A
X
(3.17)
Если определитель (3.17) отрицателен, то кривая штрихуется справа.
80
При соблюдении этого правила штриховка будет направлена внутрь области
устойчивости. При этом значения параметра А откладывается по оси абсцисс вправо,
а В – по оси ординат вверх.
3.5 Критерий устойчивости Найквиста [2,c.102-110; 3,c.133-141; 4,c.141-153]
Сформулирован в 1932 г. американским ученым Найквистом. В отличие от
критериев Гурвица и Михайлова позволяет судить об устойчивости замкнутой АС по
виду АФЧХ разомкнутой системы.
Передаточная функция разомкнутой системы:
n
nn
o
m
mm
o
cpcpc
bpbpb
pC
pB
pW
1
1
1
1
)(
)(
)(
.
При подстановке
jp
получим частотную передаточную функцию
разомкнутой системы (АФЧХ):
)()()(
)(
)(
)(
)(
jVUeA
jC
jB
jW
j
,
где АЧХ
M
M
X
Y
jWA )()(
является модулем
)(
jW
, а сдвиг
фаз
- ее аргументом (фазой).
Если изменять
от
до
, то вектор
)(
jW
своим концом
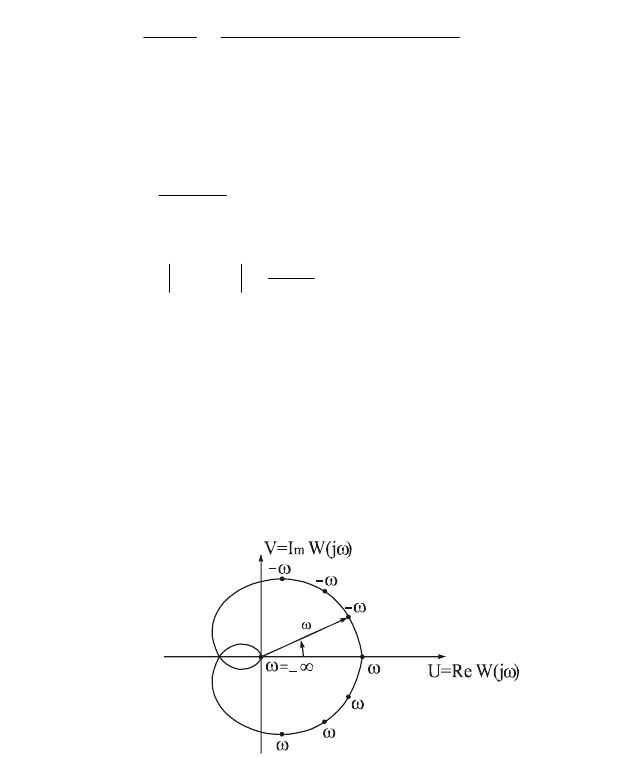
опишет на комплексной плоскости кривую, которая и называется АФЧХ (рис.p3.7).
Ветвь для отрицательных
является зеркальным отражением относительно
вещественной оси для положительных
. Поскольку в реальных системах
nm
,
то при
,
0)(
A
и точка АФЧХ, соответствующая частоте
,
попадает в начало координат.
2
3
1
= 0
)(
2
3
1
+
W ( j )
0
81

Рисунок 3.7 – График АФЧХ разомкнутой системы
3.5.1 Общая формулировка критерия Найквиста
Для устойчивости замкнутой АС необходимо и достаточно, чтобы АФЧХ
разомкнутой системы при изменении
от 0 до
охватывала точку с
координатами
0,1 j
на угол
l
против часовой стрелки, где l – число корней
характеристического уравнения разомкнутой системы, имеющих положительные
вещественные части. Если АФЧХ проходит через точку
1,0 j
, то замкнутая
система находится на колебательной границе устойчивости.
Для доказательства введем вспомогательную функцию:
)(
)(
)(
)()(
)(1)(
1
pC
pD
pC
pBpC
pWpW
, (3.18)
где
)( pW
- передаточная функция разомкнутой системы;
D(p) и С(р) – соответственно характеристические полиномы замкнутой
и разомкнутой системы.
Найдем комплекс:
)(
)(
2
)(
1
1
)(
)(
)(
)(
)(
)(
2
1
j
j
j
eA
eA
eA
jC
jD
jW
и определим угол поворота (аргумент) вектора
)(
1
jW
при изменении
от 0 до
. Этот угол по правилу деления комплексных чисел равен разности
аргументов числителя
1
и знаменателя
2
:
21
.
В п. 3.3 было показано, что в устойчивой замкнутой системе угол поворота
вектора
2
)(
1
njD
.
Если в характеристическом уравнении разомкнутой системы имеется l корней с
положительной вещественной частью, а остальные (n – l) корней имеют
отрицательные вещественные части, то согласно (3.14):
ln
2
2
.
82
