Колесников А.А. Синергетические методы управления сложными системами: энергетические системы
Подождите немного. Документ загружается.


W
hD
(s)=
ε
s
e
−st
,
t ∈ [0,t]
x
1
=∆h x
2
= p x
3
= x x
4
= p u
1
= D
u
2
= Q
D
D
=
˜
D
+ D ,
dx
1
dt
=
1
F
1
∆
e
((˜e
22
− ˜e
1
e
21
)l
1
− (˜e
12
− ˜e
1
e
11
)l
2
)+
1
e
33
∂ ¯ϕ (x
2
,x
3
)
∂x
3
V l
3
;
dx
2
dt
=
1
∆
e
(e
11
l
2
− e
21
l
1
);
dx
3
dt
=
e
32
∆
e
e
33
(e
21
l
1
− e
11
l
2
)+
1
e
33
l
3
;
dx
4
dt
=
1
e
44
(
˜
D
(x
2
,x
4
)+D − D ),
l
1
= u
1
−
˜
D
(x
2
,x
4
) − D − D ;
l
2
= u
2
+ u
1
i − (
˜
D
(x
2
,x
4
)+D )i
(x
2
) − D i
(x
2
);
l
3
= u
2
− x
3
r(x
2
)D (x
2
,x
3
);
˜
D
(x
2
,x
4
)=
˜
D
0
ρ (x
4
,ϑ
0
)(x
2
− x
4
)
ρ (x
0
4
,ϑ
0
)(x
0
2
− x
0
4
)
.

e
ij
,i,j=1,...,4 ˜e
k2
,k=1, 2
x
s
,s=1,...,3
˜e
1
e
44
˜e
1
=
∂ ¯ϕ
∂p
−
e
32
e
33
∂ ¯ϕ
∂x
V
; e
44
= V
∂ρ (x
4
,ϑ
k
= ϑ
0
k
)
∂x
4
.
D
D = D D = D
D
D D D D
u
x
4
= x
0
4
x
1
=0
x
4
= x
0
4
x
1
=0
ψ
1
= β
11
x
1
+ β
12
(
˜
D
(x
2
,x
4
)+D − D + e
44
α
3
(x
4
− x
0
4
));
ψ
2
= β
21
x
1
+ β
22
(
˜
D
(x
2
,x
4
)+D − D + e
44
α
3
(x
4
− x
0
4
))
ψ
i
=0
˙
ψ
1
(t)+α
1
ψ
1
=0,
˙
ψ
2
(t)+α
2
ψ
2
=0,

α
1
α
2
α
1
> 0 α
2
> 0
ψ
1
=0 ψ
2
=0
u
1
u
2
u
1
=
1
∆
F
⎛
⎜
⎜
⎝
f
3
˜
D
(x
2
,x
4
)+D − D
∂
˜
D
(x
2
,x
4
)
∂x
4
e
44
∂
˜
D
(x
2
,x
4
)
∂x
4
+ e
44
α
3
− f
1
f
6
+
+ f
3
f
4
+
1
∆
β
∂
˜
D
(x
2
,x
4
)
∂x
2
k
1
f
3
+ k
2
f
6
∂
˜
D
(x
2
,x
4
)
∂x
2
⎞
⎟
⎟
⎠
,
u
2
= −
1
∆
F
⎛
⎜
⎜
⎝
f
2
˜
D
(x
2
,x
4
)+D − D
∂
˜
D
(x
2
,x
4
)
∂x
4
e
44
∂
˜
D
(x
2
,x
4
)
∂x
4
+ e
44
α
3
− f
1
f
5
+
+ f
2
f
4
+
1
∆
β
∂
˜
D
(x
2
,x
4
)
∂x
2
k
1
f
2
+ k
2
f
5
∂
˜
D
(x
2
,x
4
)
∂x
2
⎞
⎟
⎟
⎠
,
k
1
= β
11
α
2
ψ
2
− β
21
α
1
ψ
1
,
∆
β
= β
11
β
22
− β
12
β
21
,
k
2
= β
12
α
2
ψ
2
− β
22
α
1
ψ
1
,
∆
F
= f
2
f
6
− f
3
f
5
,
f
1
= −
1
F
˜e
22
−˜e
12
i
(x
2
)−˜e
1
(e
21
−e
11
i
(x
2
))
∆
e
(
˜
D
(x
2
,x
4
)+D )+
+
˜e
22
−˜e
12
i
(x
2
)−˜e
1
(e
21
−e
11
i
(x
2
))
∆
e
D +
x
3
r(x
2
)
e
33
∂ ¯ϕ (x
2
,x
3
)
∂x
3
V D (x
2
,x
3
)
,
f
2
=
1
F
˜e
22
−˜e
12
i − ˜e
1
(e
21
− e
11
i )
∆
e
,
f
3
= −
1
F
˜e
12
− ˜e
1
e
11
∆
e
−
1
e
33
∂ ¯ϕ (x
2
,x
3
)
∂x
3
V
,
f
4
=
e
21
− e
11
i
(x
2
)
∆
e
(
˜
D
(x
2
,x
4
)+D )+
e
21
− e
11
i
(x
2
)
∆
e
D ,
f
5
=
e
11
i − e
21
∆
e
,f
6
=
e
11
∆
e
.
α
i
,i=1, 2 ψ
i
=0
B =
β
11
β
12
β
21
β
22
x
1
=0,
˜
D
(x
2
,x
4
)+D − D = −e
44
α
3
(x
4
− x
0
4
),
ψ
i
=0 i =1, 2

˙x
4
(t)=−α
3
(x
4
− x
0
4
).
α
3
> 0 x
4
3/α
3
x
0
4
ψ
1
=0
ψ
2
=0
x
1
=0 x
4
= x
0
4
α
i
> 0,i=1, 2
ψ
1
=0
ψ
2
=0
x
4
= x
0
4
x
3
x
1
x
2
x
4
x
0
1
x
0
2
x
0
4
x
0
2
˜
D
(x
2
,x
4
)+D − D =0
dx
3ψ
dt
=
1
e
33
(x
0
2
,x
3ψ
)
1
∆
F
(f
1
f
5
− f
2
f
4
) − x
3ψ
r(x
0
2
)D (x
0
2
,x
3ψ
)
,
∆
F
f
i
x
1
=0 x
4
= x
0
4
x
2
= x
0
2
= f(x
0
4
,D − D ) x
3ψ
γ γ =(D −D )/
˜
D
0
x
3
0, 01 ÷ 1 γ =0, 5 0, 02 ÷ 1
γ =0, 8 0, 045 ÷ 1 γ =1, 1
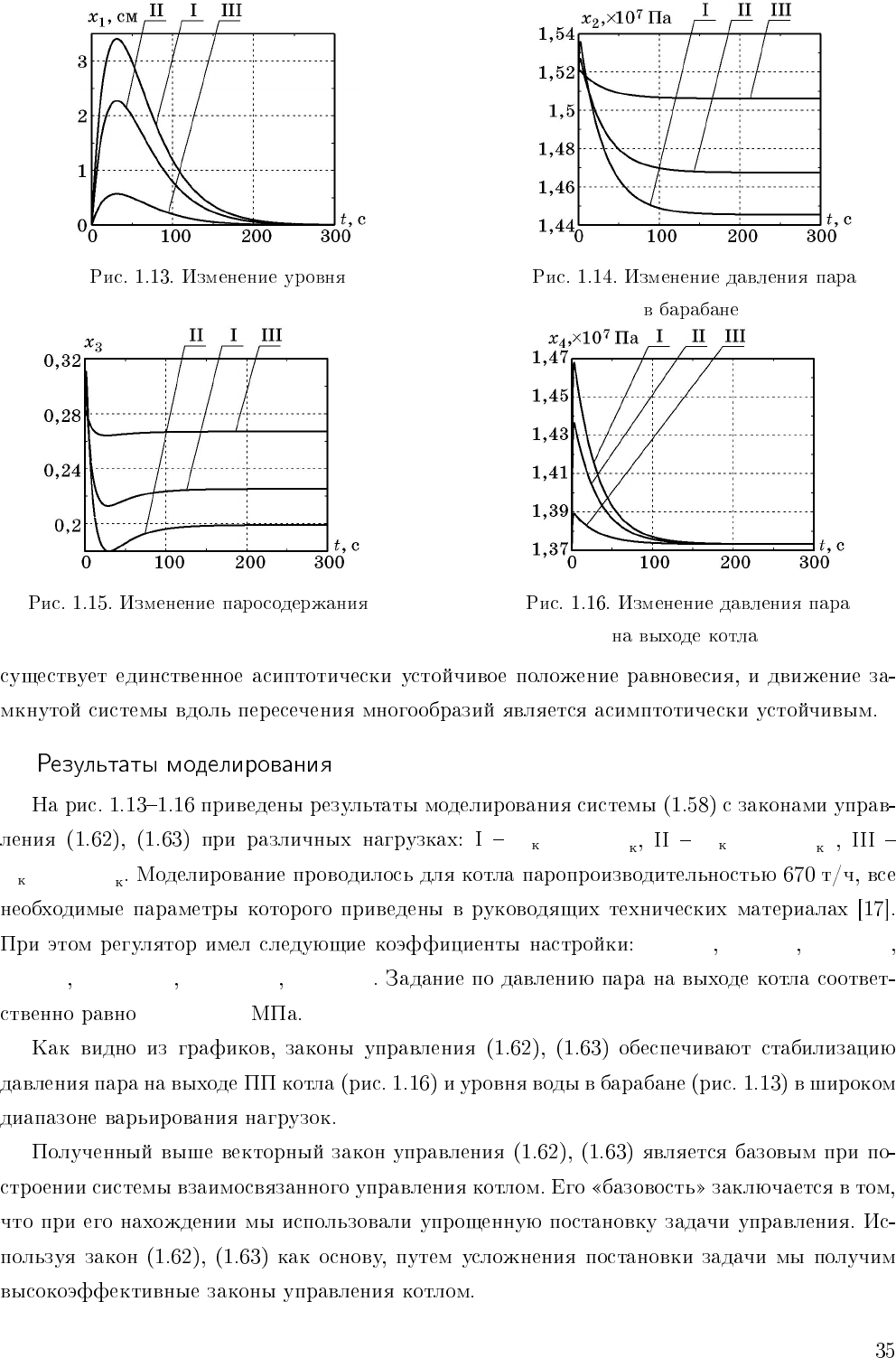
D =0, 7D
0
D =0, 8D
0
D =0, 95D
0
β
11
=1 β
12
=1 β
21
=40
β
22
=1 α
1
=1/30 α
2
=1/32 α
3
=3/2
x
0
4
=13, 73

x
1
x
4
x
3
λ
3
= −
r(x
0
2
)
e
33
(x
0
2
,x
0
3
)
D
(x
0
2
,x
0
3
)+x
0
3
∂D (x
2
,x
3
)
∂x
3
x
2
=x
0
2
,x
3
=x
0
3
,
λ
3
= −0, 1205
x
3
x
3
x
3
= F (x
2
,x
4
,D ,D ),
x
3
x
3
F (x
2
,x
4
,D ,D )
F (x
2
,x
4
,D ,D )
x
3
(x
2
,x
5
,D ,D )=β
0
+ β
1
x
2
10
6
+ β
2
x
2
10
6
2
+ β
3
x
2
10
6
3
,
β
i
= β
i
(x
2
,x
4
,D ,D )
u
1
−
˜
D
(x
2
,x
4
) − D −D =0;
u
2
+ u
1
i − (
˜
D
(x
2
,x
4
)+D )i
(x
2
) − D i
(x
2
)=0;
u
2
− x
3
r(x
2
)D (x
2
,x
3
)=0.
x
3
r(x
2
)D (x
2
,x
3
)=(
˜
D
(x
2
,x
4
)+D )(i
(x
2
) − i )+D (i
(x
2
) − i ).
D
¯ϕ

D =
2ρ
(x
2
)f (ρ
(x
2
) − ρ
(x
2
))g ¯ϕ V
k
;
¯ϕ
=
ρ
(x
2
)
ρ
(x
2
) − ρ
(x
2
)
1 −
ρ
(x
2
)
(ρ
(x
2
) − ρ
(x
2
))x
3
1+
ρ
(x
2
) − ρ
(x
2
)
ρ
(x
2
)
x
3
;
D(x
2
,x
4
,D ,D )=
˜
D
(x
2
,x
4
)+D +
i
(x
2
) − i
i
(x
2
) − i
D ,
x
2
3
−
ρ
x
3
(ρ
− ρ
)
1+
ρ
− ρ
ρ
x
3
=
k
2gf V
i
− i
ρ
r
D(x
2
,x
4
,D ,D )
2
.
x
2
3
1 −
1
Ax
3
(1 + Ax
3
)
= B
k
2gf V
D
2
(x
2
,x
4
,D ,D ),
A =
ρ
− ρ
ρ
,B=
i
− i
ρ
r
2
.
x
3
x
3
=
3
i=0
β
i
(x
2
,x
4
,D ,D )
x
2
10
6
i
x
3
D(x
2
,x
4
,D ,D ) (0, 4 ÷ 1, 4)D(x
0
2
,x
0
4
,D
0
,D
0
) x
2
0, 3x
0
2
1, 3x
0
2
x
3
(x
2
)
D(x
2
,x
4
,D ,D ) β
i
(D(x
2
,x
4
,D ,D ))
β
i
(D(x
2
,x
4
,D ,D ))
β
i
= β
i0
+ β
i1
C + β
i2
C
2
,
C =
k
2gf V
D
2
(x
2
,x
4
,D ,D )
x
3
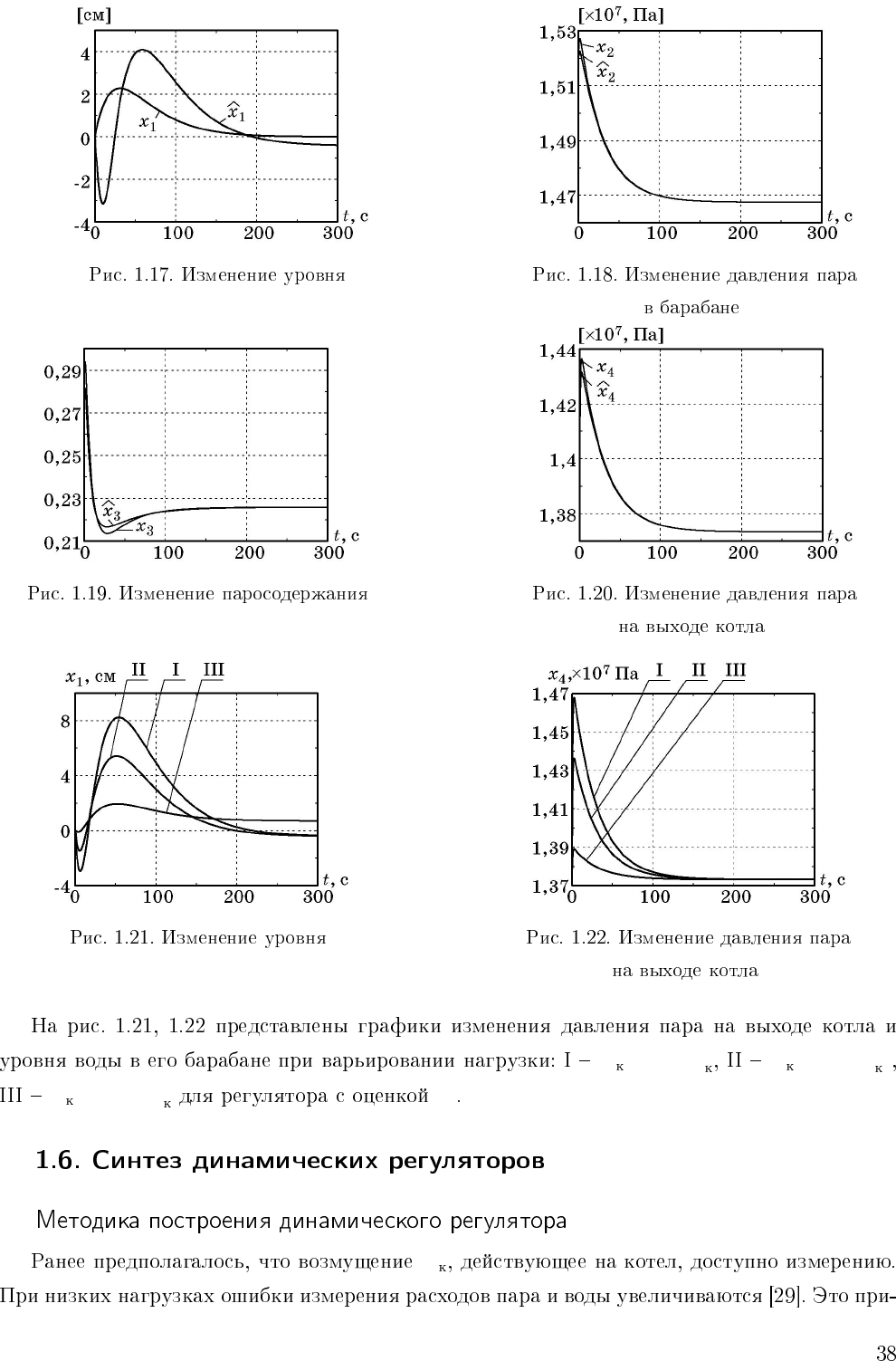
D =0, 7D
0
D =0, 8D
0
D =0, 95D
0
x
3
D

D
˙
z(t)=F(∆x),
∆x x
F ∆x =0
F(∆x)=0.
˙
x(t)=f(x, u, M),
˙
z(t)=F(∆x),
M = Cz.
ψ =0
ψ =0
˙
z(t)
˙
z(t)=F(∆x), M = Cz
M
u(x, z) F
˜
D
D
D D D
∆
e
e
11
dx
2
dt
= u
2
−
˜
D
(i
− i );
e
44
dx
4
dt
=
˜
D
− δ
1
z;
dz
dt
= δ
2
(x
4
− x
0
4
);
ψ
1
=
˜
D
− δ
1
z + α
2
e
44
(x
4
− x
0
4
).

z
ψ
1
=0
˙
ψ
1
(t)+α
1
ψ
1
=0
u
2
u
2
=
˜
D
(i
− i ) −
∆
e
e
11
∂
˜
D
∂x
2
∂
˜
D
∂x
4
+ α
4
e
44
1
e
44
(
˜
D
− δ
1
z)+α
1
ψ
1
− δ
1
δ
2
(x
4
− x
0
4
)
.
u
2
α
1
> 0
ψ
1
=0
˙x
4
(t)+α
2
(x
4
− x
0
4
)=0.
α
2
> 0
x
4
x
4
= x
0
4
D =0, 8D
0
D =0, 9D
0
D =0, 95D
0
β
11
=1 β
12
=1 β
21
=40 β
22
=1 α
1
=1/30 α
2
=1/32 δ
1
=1 δ
2
=1/x
0
5
x
0
4
=13, 74
z δ
1
=1 D
D =0, 8D
0
= 148, 8 D =0, 9D
0
= 167, 5
D =0, 95D
0
= 176, 8
D
x
4
