Кочергин В.И. Теория многомерных цифро-векторных множеств

Подождите немного. Документ загружается.

Глава 3

150

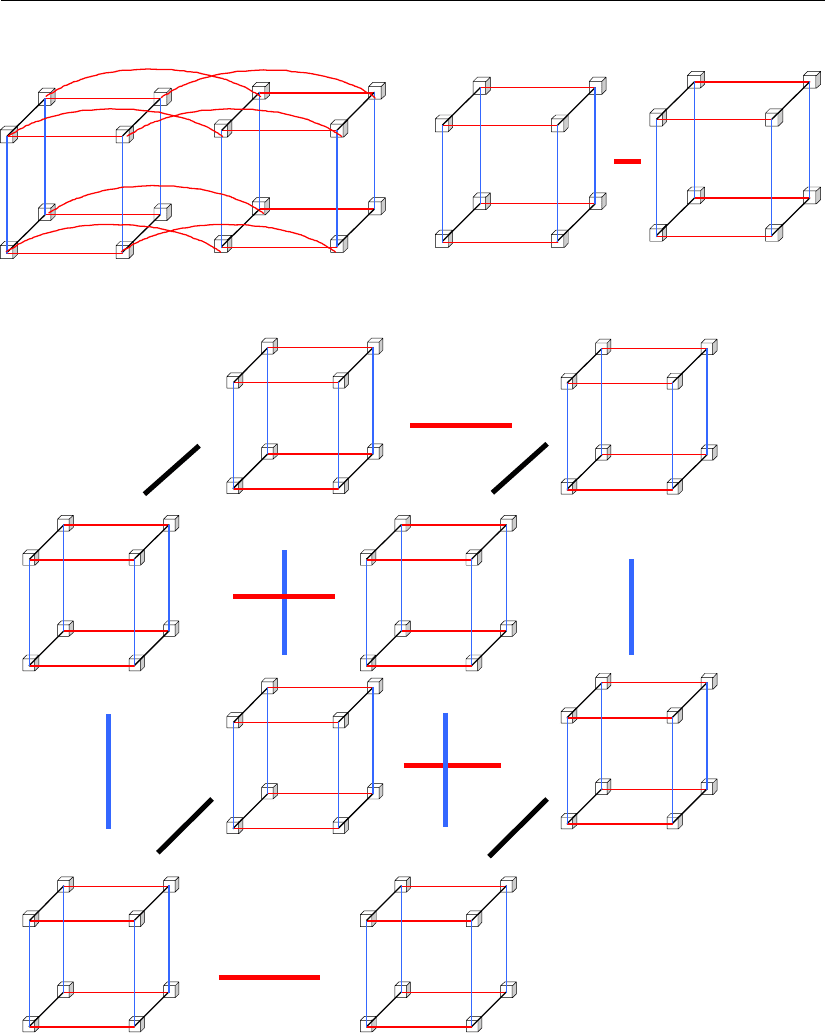
На рис. 3.9 изображен «гиперкуб», составленный из двух «кубов», каждый из

которых представляет собой основание системы счисления n = 2

(0–7), а вместе

они представляют собой основание системы счисления n = 2

(0–15). Здесь приве-

дены два эквивалентных варианта изображения этого «гиперкуба».

1 0

0 1

Рис. 3.9

Рис. 3.10

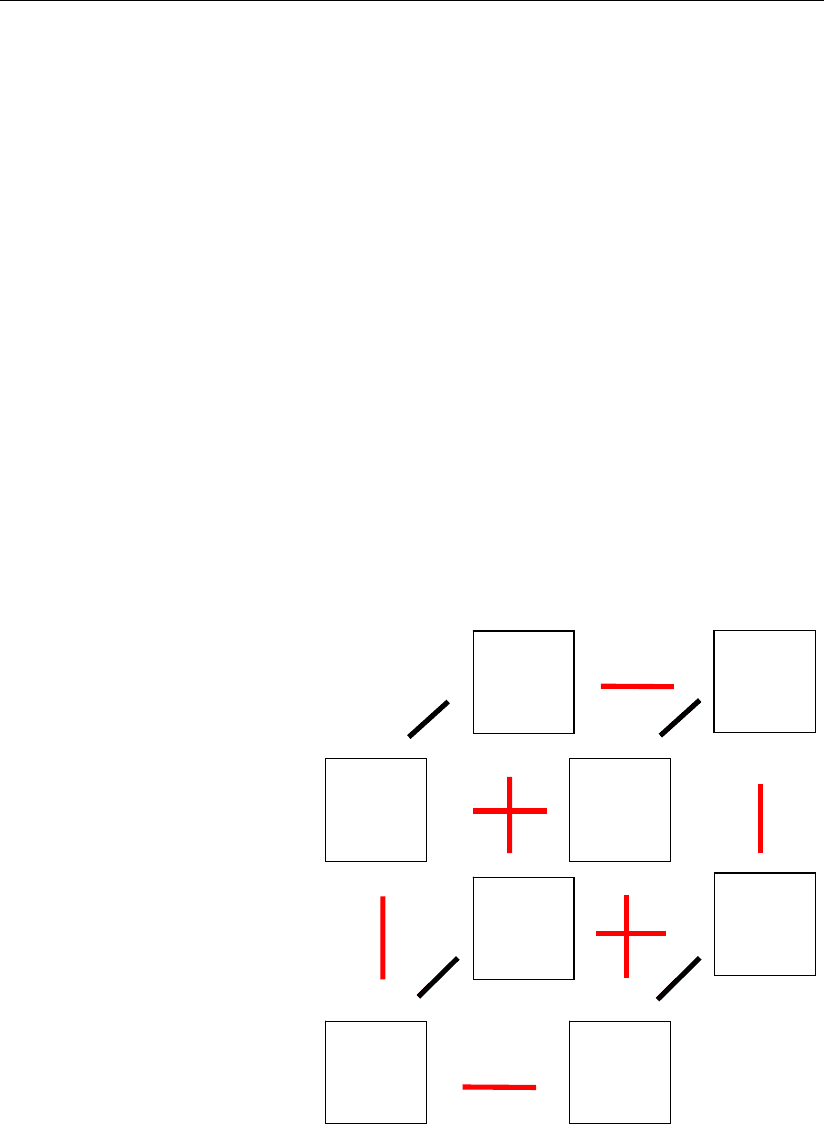
Контролеспособность позиционных систем счисления

151

В первом варианте показаны все связи, определяющие одиночные ошибки,

которые переводят одни кодовые комбинации в другие, где натуральные числа

представлены двумя разрядами: первый разряд содержит цифры (0–7), второй –

цифры 0, 1. Следовательно, первый «куб» представляет цифру 0 второго разря-

да, а второй куб – цифру 1 этого же второго разряда. Все одноименные элемен-

тарные ячейки этих «кубов» соединены линиями, определяющими переход ко-

довых комбинаций при одиночных ошибках.

Второй вариант представления «гиперкуба» более простой: в нем номера

элементарных ячеек представлены цифрами одного разряда (0–15), а все соеди-

нения между двумя трехмерными «кубами» представляются общей жирной

чертой, которая параллельна здесь оси координат x

. Именно такой вариант

представления «гиперкубов» будет использоваться нами в дальнейшем.

Данные табл. 3.1.1 отражаются в половине «гиперкуба» шестимерного

пространства рис. 3.10. Этот «гиперкуб» состоит из восьми трехмерных «ку-

бов», каждый из которых определяется и может задаваться рядом последова-

тельных натуральных чисел (0–7), (8–15), (16–23), (24–31), …, (56–63). Жирные

линии, параллельные осям координат x

, x

, соединяют соответствующие

«кубы» и определяют одиночные ошибки, которые переводят натуральные чис-

ла одного «куба» или «гиперкуба» в другие числа одинаковых «кубов» или

«гиперкубов». Например, все числа «куба» (0–7) при одиночных ошибках мо-

гут переходить в соответствующие числа внутри этого «куба», а также в числа

«кубов» (8–15), (16–23), (32– 9) и т.д.

Очевидно, что не пред-

ставляет какого-либо труда

изобразить «гиперкуб» любой

мерности, поскольку увели-

чение мерности «гиперкуба»

выполняется простым изо-

бражением ему подобного,

соединенного с первым жир-

ной чертой, параллельной со-

ответствующей координате

трехмерного цифрового про-

странства. Причем в качестве

исходного может быть при-

нят не «куб», а «гиперкуб»

любой мерности. Например,

если в качестве исходного

принять «гиперкуб» мерности

четыре (рис. 3.9), определяе-

мый цифрами (0–15), то «ги-

перкуб» мерности семь может

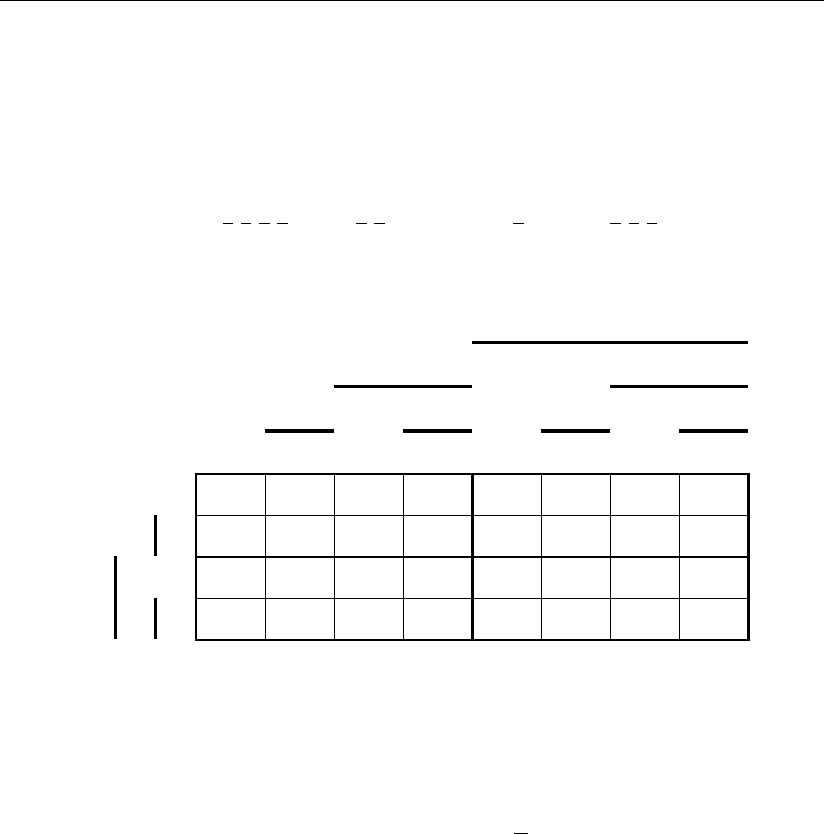
быть изображен рис. 3.11 и

т.д.

112–127 96–111

80–95

64–79

48–63 32–47

0–15

Рис. 3.11

16–31

Глава 3

152

3.2. Многофазный код

Важное место в системах электропривода и электропитания занимает мно-

гофазный код, являющийся естественным кодом целого ряда их устройств, где

используются многофазные напряжения.

Целесообразно начать анализ с многофазного кода, поскольку этот тип ко-

да наиболее исследован и для него решена задача обнаружения и исправления

ошибок на основе особой физической структуры кода. Эта особенность кода

заключается в возможности представления любого штатного состояния как со-

ставной части двух непрерывных множеств: логических нулей и единиц.

Известная процедура обнаружения и исправления ошибок [2] заключается

здесь именно в контроле непрерывности этих множеств и восстановлении этой

непрерывности при любых ее нарушениях. Следовательно, имеется возмож-

ность сравнить два способа контроля многофазного кода, отмеченные выше.

В качестве примера для рассмотрения выберем пятифазный код (n=10). Из

возможных кодовых комбинаций многофазный код использует 2k штатные

комбинации, которые для пятифазного кода (k=5) соответствуют десяти сигна-

лам обычного цифрового кода (ОЦК) 0–9, а остальные кодовые комбинации яв-

ляются запрещенными и каждая из них представляется как ошибочная выдача

одновременно нескольких сигналов ОЦК.

Последовательно записанные штатные кодовые комбинации, соответст-

вующие цифрам от 0 до 9, и образуют сигналы пятифазного кода a

– a

Связь между сигналами a

– a

и эквива-

лентными им сигналами ОЦК приведена на

рис. 3.12.

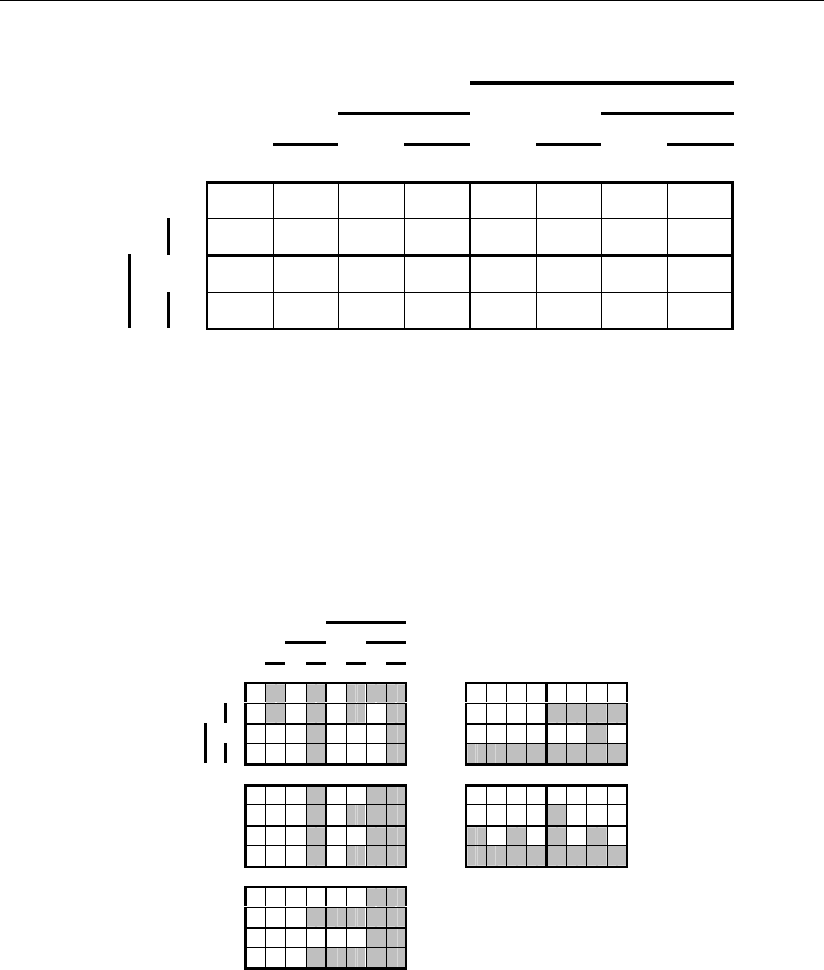
На рис. 3.13 приведены все 32 кодовые

комбинации в двухмерном цифровом про-

странстве, где, например, по одной координа-

те отложены позиции сигналов первых трех

разрядов a

, a

, а по второй – остальных

двух разрядов a

, a

. На пересечении коорди-

нат здесь записаны эквивалентные кодовым

комбинациям сигналы ОЦК – как штатные

(выделены цветом), так и ошибочные.

Следует отметить, что эти сигналы соответствуют преобразованиям пяти-

фазного кода в сигналы ОЦК по алгоритму

0 = a

, 1 = a

, 2 = a

, 3 = a

, 4 = a

5 = a

, 6 = a

, 7 = a

, 8 = a

, 9 = a

и их не следует путать с ошибочными сигналами, обозначение которых было

приведено выше.

0 1 2 3 4 5 6 7 8 9

Рис. 3.12

Контролеспособность позиционных систем счисления

153

Покрытие «площади», ограниченной этими ошибочными сигналами ОЦК,

определяет все возможные варианты построения логической схемы обнаруже-

ния «немногофазности», а покрытие «площади», ограниченной штатными сиг-

налами для цифр 0–9, определяет «многофазность» кода, одним из вариантов

которой является логическая функция

λ = a

∨ a

(3.2.1)

где первое слагаемое покрывает штатные сигналы 0, 1, второе – 2, 3 и т.д.

Для обеспечения устойчивости работы счетчиков многофазного кода [3],

когда при каких-либо сбоях и выходе счетчика из устойчивых рабочих режимов

необходимо вернуть его в одно из устойчивых состояний, например начальное,

используется именно сигнал «немногофазности» λ, хотя наиболее правильным

решением было бы возвращение счетчика в то рабочее состояние, из которого

он был только что выведен. Решить эту задачу положительно можно только по-

сле анализа контролеспособности многофазного кода.

3.3. Анализ контролеспособности многофазного кода

методом многомерных цифровых множеств

Этот анализ проведем, как ранее условились, на примере основания систе-

мы счисления n = 10.

В соответствии с распределением эквивалентных пятифазному коду сигна-

лов ОЦК в ячейках двухмерного пространства, а также одиночных и двойных

ошибок на рис. 3.14 приведено заполнение ячеек этого пространства указанны-

ми сигналами.

0 1

0,2,6

0,3,7 1,3,7 0,3,6

0,4,8 1,4,8

0,2,4,6,8

2,4,8 0,4,7 1,4,7 0,4,6

1,5,9 2,6,9 2,5,9 3,7,9

1,3,5,7,9

3,6,9 3,5,9

1,5,8 2,6,8 2,5,8

1,5,7

6 5

Рис. 3.13

Глава 3

154

В ячейках, которые уже заняты сигналами одиночных ошибок, сигналы

двойных ошибок не приведены.

Из этого представления видно, что только одиночные ошибки имеют воз-

можность исправления (один из пяти) и обнаружения (четыре из пяти). Двой-

ные же ошибки занимают только две оставшиеся от размещения более вероят-

ностных сигналов ячейки и не могут быть исправлены.

В соответствии с рис. 3.14 и зависимостью сигналов многофазного кода

– a

от сигналов ОЦК (см. рис. 3.12) для каждого геометрического образа

сигналов a'

– a'

выберем ту ячейку пространства, которая однозначно включа-

ется в эти сигналы. Эта процедура позволяет получить в многомерном про-

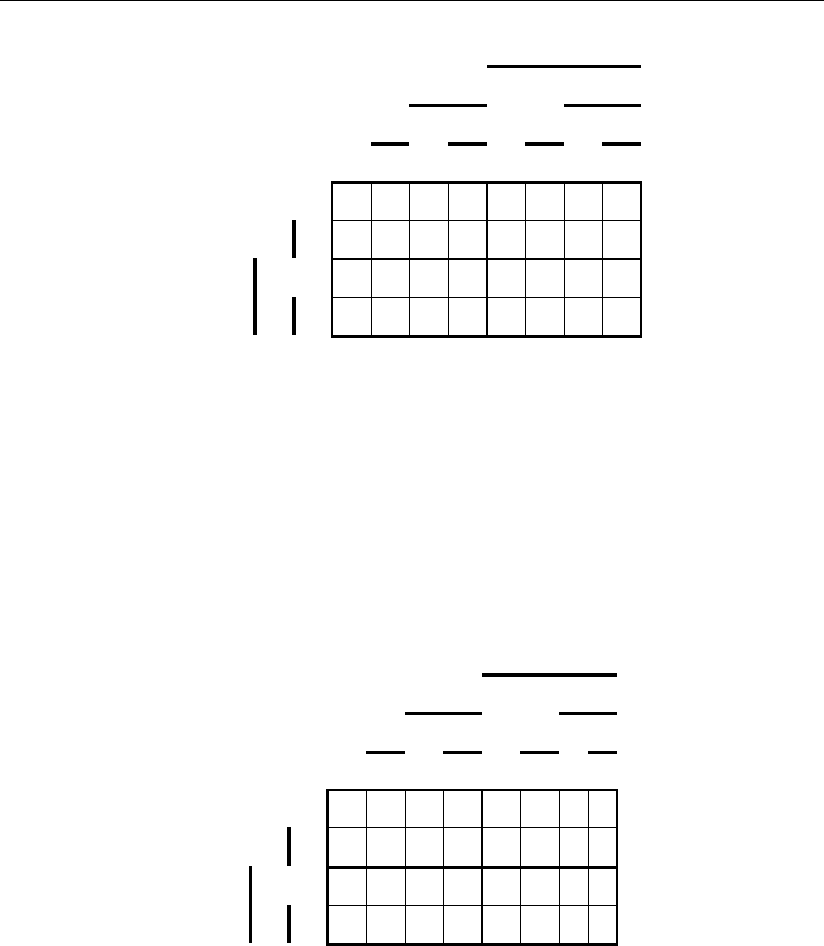
странстве (рис. 3.15) пять фигур для сигналов многофазного кода, покрытие ко-

торых определяет логическую функцию блока исправления ошибок.

0,1

1,0

2,1

3,2

4,3

9,0

8,7

7,6

6,5

5,4

Рис. 3.14

Рис. 3.15

Контролеспособность позиционных систем счисления

155

0 1

2 0

3 3

0 2

7 4

0,4,6

9 2

9 0

8 8

5 7

6 5

Рис. 3.16

Пропуск исправленных сигналов a'

– a'

через блок формирования сигна-

лов ОЦК даст распределение сигналов ОЦК в ячейках пространства, как приве-

дено на рис. 3.16. Это распределение полностью выполняет функции исправле-

ния ошибок наибольшей вероятности, а остальные одиночные ошибки исправ-

ляются стихийно в пользу каких-либо альтернативных вариантов равной веро-

ятности. Причем здесь имеются ячейки под номерами 17, 29, 21,

где установка

сигналов ОЦК произведена не в альтернативном, а в худшем варианте, чем это

предлагается на рис. 3.14.

Для исправления этого не совсем удачного размещения сигналов ОЦК

можно заранее принять волевое решение о выборе конкретной цифры в ячейке

в соответствии с альтернативами рис. 3.14.

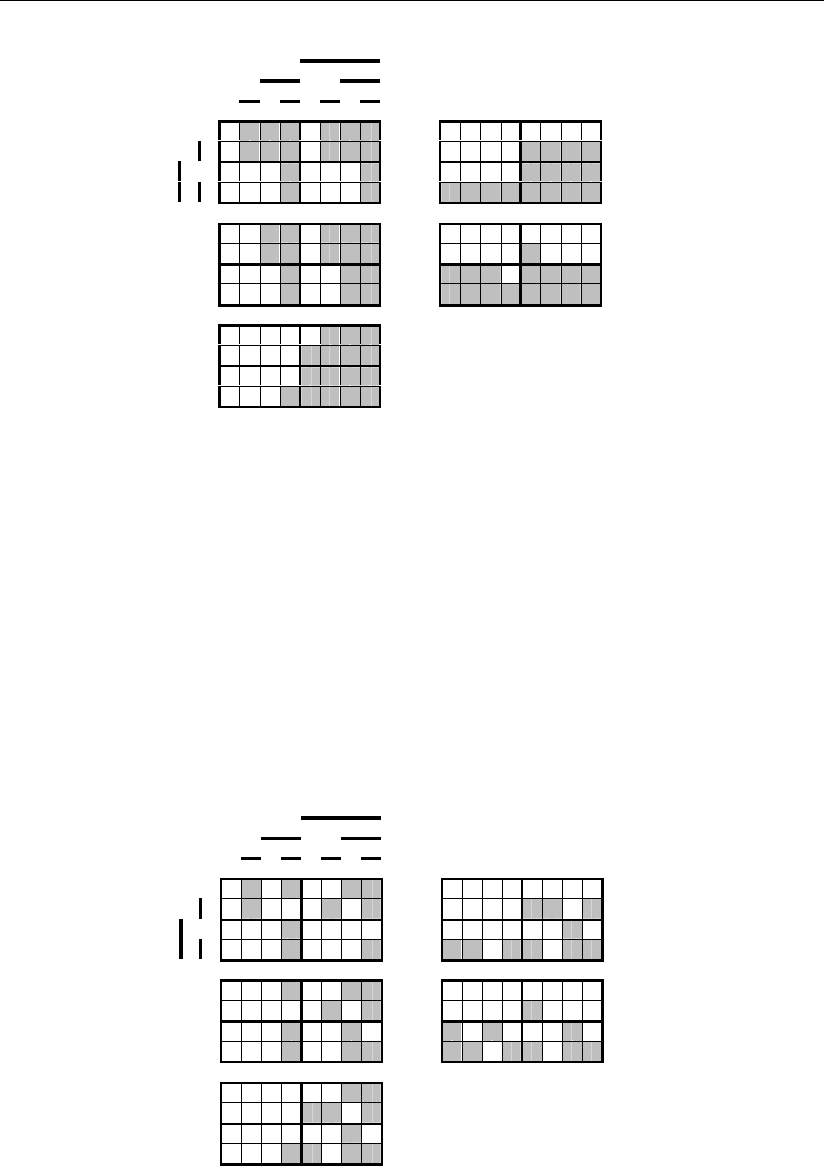
Такое распределение приведено на рис. 3.17, а соответствующие ему гео-

метрические образы сигналов a'

– a'

– на рис. 3.18. Логические функции, опре-

деляющие покрытие фигур этих сигналов, более просты, чем покрытие фигур

рис. 3.15, а результат исправления предпочтительней.

0 1

2 0

2 2

7 4

9 2

7 7

8 8

5 7

Рис. 3.17

Глава 3

156

Именно такой подход наиболее прост и эффективен для обеспечения ус-

тойчивости счетчиков многофазного кода.

В блоках машинной арифметики, где выбор каких-либо альтернативных ва-

риантов распределения сигналов ОЦК не допустим, поскольку приводит к ава-

рийным ситуациям, рабочими режимами являются только штатные состояния

кода и те состояния, которые непрерывно исправляются контролирующими

устройствами.

Для этого варианта построения блока исправления ошибок в многомерном

пространстве заполняются только ячейки штатного состояния и ячейки, где

располагаются исправленные кодовые комбинации.

Геометрические образы исправленных сигналов (рис. 3.19) для этого вари-

анта более сложные для покрытия.

Рис. 3.19

Рис. 3.18

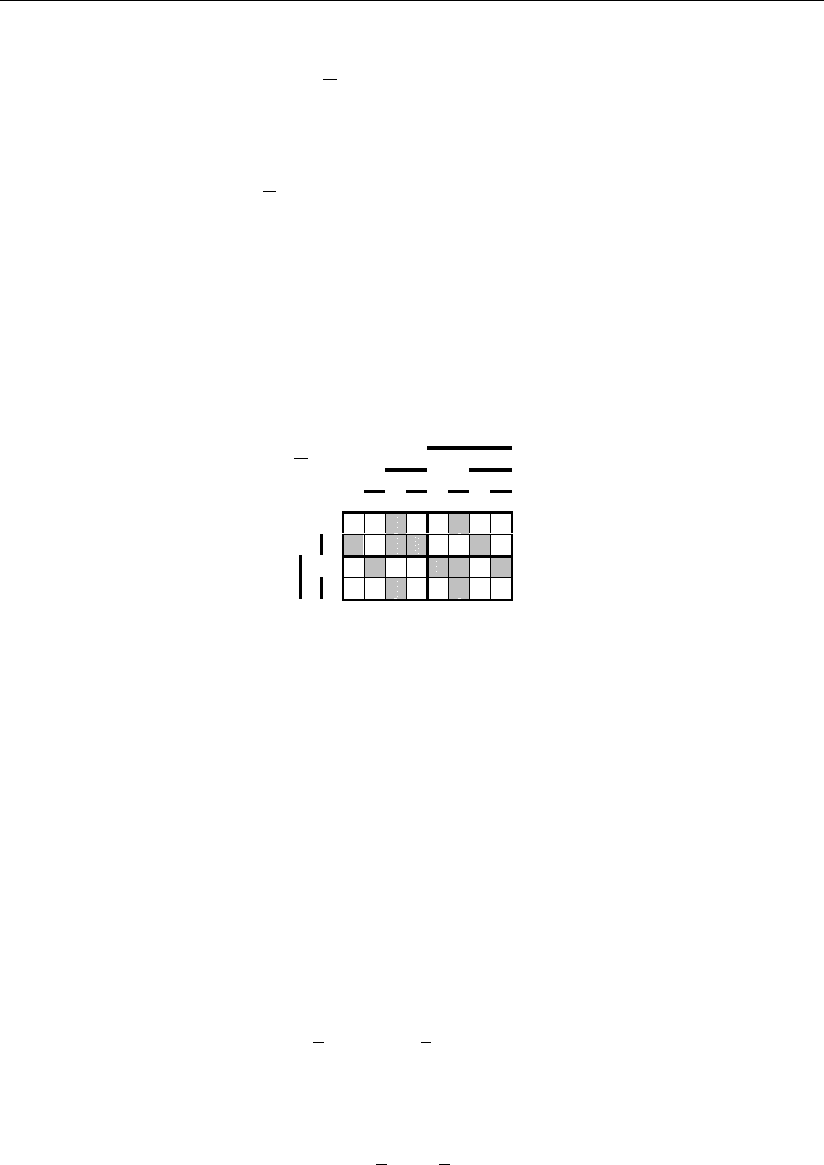
Контролеспособность позиционных систем счисления

157

В этом варианте обязательно необходимо определение бесконтрольной не-

рабочей области пространства λ, появление которой требует остановки вычис-

лительного процесса, поскольку в этой области пространства сигналы кода не-

действительны. При этом в нерабочую область пространства не должны вхо-

дить нулевые значения сигналов кода, которые эквивалентны цифре 0.

Известность сигнала λ позволяет использовать более простые геометриче-

ские образы сигналов a'

– a'

, чем такие же сигналы рис. 3.19, например сиг-

налы рис. 3.18.

Определение оптимальных, т.е. более простых для покрытия геометриче-

ских образов сигналов a'

– a'

, будет сформулировано следующим образом:

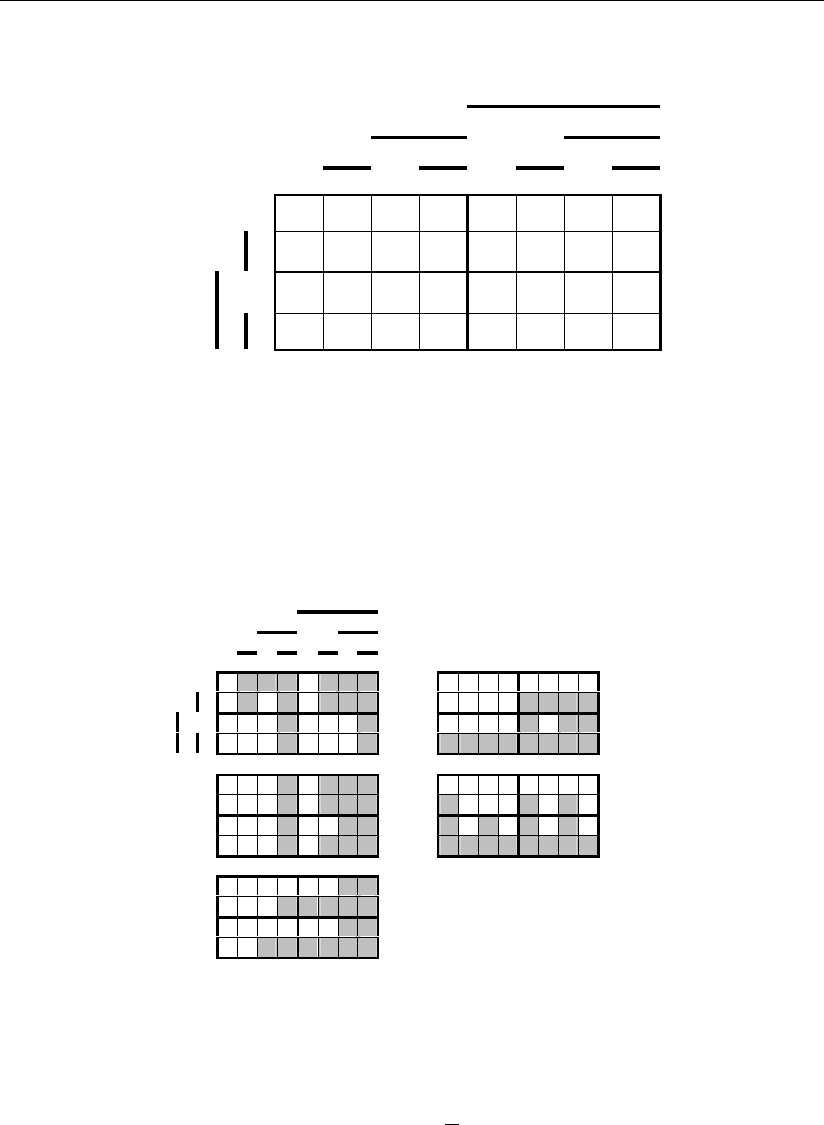
обязательной частью этих оптимальных образов должны быть фигуры, напри-

мер рис. 3.19, а поиск более простых фигур должен производиться добавлением

к ним любых ячеек пространства, геометрический образ которого представлен

на рис. 3.20.

Рис. 3.20

Весьма прост по реализации и наиболее эффективен по быстродействию ал-

горитм исправления ошибок, например, многофазных кодов, в записи Либау–

Крейга, который основан на контроле и сохранении непрерывности множеств

логических нулей и единиц этого типа кодов [2]. Эти непрерывные множества

всегда имеются при последовательной записи прямых и инверсных сигналов

этих кодов. При этом здесь появляется возможность исправления не только оди-

ночных, но и двойных, тройных и т.д. ошибок, а также различных пачек таких

ошибок. Возможности этого алгоритма возрастают с увеличением числа фаз ко-

да, но наиболее ценным является исправление именно одиночных ошибок.

В соответствии с этим алгоритмом исправление, например, одиночных

ошибок пятифазного

кода будет производиться по следующим логическим

формулам:

= a

∨

∨ a

;

= a

∨

∨ a

;

= a

∨

∨ a

;

= a

∨

∨ a

;

= a

∨

∨ a

(3.3.1)

Глава 3

158

На основании (3.3.1) и рис. 3.13 распределение сигналов ОЦК в ячейках мно-

гомерного пространства для этого варианта реализации приведено на рис. 3.21, а

геометрические образы исправленных сигналов (a'

– a'

) – на рис. 3.22.

Рис. 3.22

Несмотря на то, что данный алгоритм не следует альтернативам распреде-

ления сигналов рис. 3.14, все исправляемые одиночные ошибки он действи-

тельно исправляет, а при наличии сигнала λ

(рис. 3.20), что требуется при лю-

бых вариантах, здесь действительно аппаратурные затраты малы и осуществля-

ется полное выполнение функций контроля и исправления ошибок.

0 1

2 0

3 3

1,5,9,

3,7

7 4

9 2

8 0,2,4,

6,8

8 8

5 7

6 5

Рис. 3.21

∼

Контролеспособность позиционных систем счисления

159

3.4. Анализ контролеспособности кодов Хемминга

методом многомерных цифровых множеств

Одним из широко известных в технике передачи информации является код

Хемминга, предназначенный, например, для исправления одной ошибки или

обнаружения двух и исправления одной ошибки [11].

Коды Хемминга имеют несколько контрольных разрядов, каждый из кото-

рых контролирует по четности (нечетности) свою группу разрядов. Эти группы

формируются таким образом, чтобы по данным контрольных разрядов можно

было бы с определенной вероятностью указать сбой соответствующего разряда.

С этой целью первый контрольный разряд контролирует по четности либо

нечетности все нечетные информационные разряды кода. В нем при передаче

информации записывается такая цифра, чтобы число единиц в контролируемых

разрядах совместно с этим контрольным разрядом было нечетным (четным).

Если при приеме и проверке кода окажется, что число единиц в нечетных раз-

рядах и первом контрольном разряде четное (нечетное), то это с определенной

вероятностью будет свидетельствовать об ошибке в нечетных разрядах. В про-

тивном случае имеется ошибка в четных разрядах или ее вообще нет.

Следовательно, сигнал о наличии ошибки в нечетных разрядах является

младшим разрядом двоичного номера разряда с ошибкой.

Второй контрольный разряд контролирует по четности (нечетности) все

разряды кода, которые имеют одинаковые цифры во втором разряде своего но-

мера, третий контрольный разряд – все разряды, имеющие одинаковые цифры в

третьем разряде своего номера, и т.д.

Исходя из изложенного, для определения следующего вероятного номера

разряда с ошибкой необходимо сформировать аналогичную функцию от разря-

дов с номерами 2, 3, 6, 7, ... и вторым контрольным разрядом и т.д.

Все это можно наглядно представить в табл. 3.4.1, где обозначены номера

информационных разрядов, которые контролируются соответствующими кон-

трольными разрядами.

В литературе по теории информации высоко оцениваются возможности ко-

дов Хемминга по контролеспособности при приеме и передаче информации, а в

публикациях по вычислительной технике эти достоинства кодов Хемминга

обесцениваются утверждением о непригодности этих кодов для выполнения

Таблица 3.4.1

Информационные разряды Контрольные разряды

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15