Князев Б.А. Низкотемпературная плазма и газовый разряд
Подождите немного. Документ загружается.


1.4.3. Линейчатое излучение. Вероятность перехода. Сила осциллятора
Вероятность перехода между дискретными уровнями k и m атомной системы (коэффициент Эйнштейна для
спонтанного излучения) равна
A
km
[с
−1
]=
4ω
3
km
3c
3
|D
km
|
2
g
m
, (1.4.24)
где g
m
– статвес конечного состояния, D
km
– матричный элемент дипольного момента атомной системы
D =
N
s=1
er ,
а r
- координата s-го электрона атома относительно ядра. Частота излучения, испускаемого или поглоща-
емого при переходе между этими уровнями, равна
ω
km
=
E
m
−E
k
. (1.4.25)
Время жизни уровня k по отношению к радиационному распаду находится суммированием обратных веро-
ятностей излучения на все нижележащие уровни
τ =
m
A
−1
km
.
Введем F
ω
- форму спектральной линии, пронормировав ее так, что ∫ F
ω
dω =1. В отсутствие внешних
возмущений Ее ширина ∆ω, в соответствии с принципом неопределенности, пропорциональна τ
−1
= A
km
.
Эта “естественная” ширина линии для разрешенных (дипольных-дипольных) переходов равна по порядку
величины ∆ω ∼ 10
8
с
−1
, что много меньше частоты перехода ω
0
∼ 10
15
с
−1
. Линия имеет лоренцовский
контур
F
ест
ω
= ε
ω
=
γ
2π
1
(ω − ω
0
)
2
+(γ/2)
2
,
∞
0
ε(ω) dω =1, (1.4.26)
где γ – постоянная затухания. Переходя к сечению поглощения фотона, для классического случая выну-
жденных колебаний упруго связанного электрона в поле электромагнитной волны E = E
0
sin ωt найдем
σ
ω
=
πe
2
mc
γ
(ω − ω
0
)
2
+(γ/2)
2
, (1.4.27)
где γ =∆ω – коэффициент затухания.
Для естественного уширения (1.4.27) γ = A
km
, и сечение поглощения в центре линии равно
σ
max
ω
0
4πe
2
mcγ
10
−9
см
2
,
что много больше газокинетического сечения πa
2
. В классическом приближении площадь под спектральной
линией осциллятора даже при наличии столкновений является константой, не зависящей от ширины линии
γ. В расчете на один осциллятор, в соответствии с общепринятой традиционной нотацией, она равна [2]
σ
ω
dν =
1
2π
σ
ω
dω =
πe
2
mc
=2.64 ·10
−2
см
2
/с . (1.4.28)
60

Действительно, при резонансном возбуждении осциллятора (ω = ω
0
) амплитуда колебаний растет про-
порционально времени от последнего столкновения r
a
(t) ∼ t. Между столкновениями набирается энергия
W ∼ r
2
a
∼ τ
2
c
, которая при следующем столкновении переходит в хаотическую. Тогда энергия отбираемая
от поля за секунду, которая пропорциональна величине σ
ω
,есть
W
τ
c
∼
r
2
a
τ
c
∼
τ
2
c
τ
c
= τ
c
. (1.4.29)
Поскольку ∆ω ∼ τ
−1
c
,то∫ σ
ω
dν ∼ σ
max
ω
· ∆ω ∼ (W/τ
c
) · ∆ω =const.
Если атом взаимодействует с окружающей средой, то это приводит к дополнительному уширению спек-
тральной линии. Механизмы уширения мы рассмотрим в следующем разделе, а сейчас получим полезные
соотношения, описывающие вероятность переходов для линий с некоторым реальным сечением σ
ω
. Энер-
гия, поглощаемая на данном переходе в 1 см
3
за 1 с, вне зависимости от характера уширения линии равна
4πn
m
I
ω
σ
ω
dω ,
где I
ω
[эрг/с см
2
с
−1
ср] – “интенсивность” излучения, а S = I
ω
(Ω)dωdΩ – физически измеримая вели-
чина, называемая плотностью потока энергии. Если I
ω
const в пределах линии, то ее можно вынести из
под интеграла и площадь линии служит мерой поглощательной способности вещества в линии.
Используя принцип детального равновесия, известные соотношения для термодинамически равновес-
ного излучения и распределение Больцмана для заселенностей уровней, получим
σ
ω
=
g
k
g
m
π
2
c
2
ω
2
A
km
· F
ω
=⇒
σ
ω
dν =
g
k
2g
m
πc
2
ω
2
A
km
. (1.4.30)
Пронормировав выражение (1.4.30) на площадь классического осциллятора (1.4.28) мы получим величину,
называемую силой осциллятора, которая, по соглашению, для поглощения считается положительной
f
mk
=
(∫ σ
ω
dν)
πe
4
/mc
=
g
k
2g
m
mc
3
e
2
ω
2
km
A
km
. (1.4.31)
Сила осцилляторя представляет собой число воображаемых классических осцилляторов, которое обеспечило
бы точно такое же поглощение, как и реальная линия. Силы осцилляторов для поглощения и излучения
связаны между собой соотношением
−g
k
f
km
= g
m
f
mk
.
Величины f
km
подчиняются правилу сумм
m
f
km
= N,
где N – полное число электронов в атомной системе, причем суммирование ведется по всем состояниям
дискретного и непрерывного спектров. Силы осцилляторов практически всех линий протабулированы. Их
можно найти, например, в [4, 26, 27, 28]. Для примера некоторые из них приведены в Таблице 6.
61

Элемент H H N He Na Hg
λ, A 6563(H
α
) 5876 5890 5461
переход 2s −3p 2p − 3s 2 p − 3d 2p
3
p
0
− 3 d
3
D 3s − 3p 6s6p − 6s7s
f 0.416 0.014 0.695 0.62 0.98 0.08
Таблица 6: Силы осцилляторов некоторых переходов.
Рис. 23: Вероятность излучательных переходов с уровня k =15водородоподобного атома на
нижележащие уровни m.
Вероятность перехода можно теперь записать в виде
A
km
=
2e
2
ω
2
km
g
m
mc
3
g
k
f
mk
=3.79 ·10
9
(E
k
−E
m
)
2
Ry
2
|f
km
|. (1.4.32)
Для водородоподобных атомов f
km
описывается квазиклассической формулой Крамерса, погрешность ко-
торой составляет ∼ 30% при всех k и m,
f
km
32
3π
√
3
1
k
5
1
m
3
1
(1/k
2
−1/m
2
)
3
3.9
1
k
5
1
m
3
Ry
E
k
−E
m
3
. (1.4.33)
Подставив (1.4.33) в (1.4.32) и учитывая множитель Z
4
, получим для водородоподобных атомов
A
km
=
1.6 · 10
10
Z
4
k
3
m(k
2
−m
2
)
. (1.4.34)
Для k =2, m =1, Z =1получим
A
21
=
1.6 · 10
10
8 · 1(4 −1)
=
160 ·10
8
32
=5· 10
8
c
−1
.
Согласно табличным данным [16], A
21
=6.26 · 10
8
с
−1
(g
2
/g
1
=6/2). Видно, что совпадение теории и
эксперимента достаточно хорошее для оценок. Для переходов на нижние уровни (m<<k)
A
k,m<<k
1.6 ·10
10
Z
4
k
5
m
.
62

Вероятность максимальна при переходе в основное состояние (m =1). Для перехода на соседнее нижнее
состояние вероятность в два раза меньше
A
k,k−1
=
1.6 · 10
10
z
4
k
3
(k − 1)[k
2
− k
2
+2k − 1]
0.8 ·10
10
Z
4
k
5
. (1.4.35)
Экстремальное значение A
k
, найдем, приняв нулю производную по m знаменателя формулы
[k
3
m(k
2
−m
2
)]
= k
3
[(k
2
− m
2
)+m · (−2m)] = k
3
(k
2
− 3m
2
) . (1.4.36)
Поскольку вторая производная −6k
3
m<0, при m = k/
√
3 A
km
принимает минимальное значение:
A
k,k/
√
3
1.6 · 10
10
Z
4
k
5
· 0.38 k
. (1.4.37)
Зависимость вероятности перехода от номера нижнего уровня, вычисленная из (1.4.34), приведена на
рисунке (23). Если зафиксировать нижнее состояние, то вероятности переходов с высоких уровней значи-
тельно меньше, чем с ближайших, что демонстрируется рисунком 24). Суммарную вероятность радиацион-
Рис. 24: Вероятность излучательных переходов на уровень m =1водородоподобного атома с
верхних уровней k.
ного распада уровня k можно оценить (см. [3]) как
A
k
=
m<k
A
km
=
1.6 · 10
10
Z
k
5
ln
k
3
− k
2
. (1.4.38)
Приведенные выше выражения для A
km
и f
km
можно использовать и для неводородоподобных атомов,
если использовать в них эффективные квантовые числа
k
∗
=
Z
2
Ry
E
k
∗
, (1.4.39)
где E
k
∗
– реальная энергия связи данного уровня многоэлектронного атома.
63

Легко видеть, что верхние (ридберговские) состояния атомов имеют очень большое время жизни по
сравнению с нижними (∼ k
−5
). Поскольку и энергия связи их сопоставима с температурой газа, то заселен-
ность верхних уровней в значительной мере определяется столкновениями. С ростом плотности вероятность
столкновительных переходов начинает превышать вероятность испускания фотона для все более глубоких
уровней.
1.4.4. Доплеровское уширение. Фойгтовский профиль
Для изолированного атома контур линии – лоренцовский (1.4.26), и естественная ширина линии γ ≡ γ
km
равна сумме радиационных ширин начального γ
k
и конечного γ
m
состояний. Поскольку атомы и ионы плаз-
мы движутся, то происходит смещение спектральной линии излучающего атома вследствие эффекта Доплера
ω = ω
0
1+
v · n
c
, (1.4.40)
где n – единичный вектор в направлении наблюдения. Если распределение атомов по скоростям максвел-
ловское, то вероятность, что составляющая скорости в направлении наблюдения равна [v
x
,v
x
+ dv
x
] есть
dp(v
x
)=
M
2πT
exp
−
Mv
2
x
2T
dv
x
, (1.4.41)
а контур линии примет вид
ε
ω
= ε
0
exp
−
Mc
2
2T
ω − ω
0
ω
0
2
. (1.4.42)
Сечение поглощения при этом, с учетом нормировки
σ
ω
km
dν =
πe
2
mc
f
km
,
равно
σ
ω
km
=
2π
2
e
2
mc
f
km
∆ω
D
√
π
exp
−
ω − ω
km
∆ω
D
2
, (1.4.43)
где
∆ω
D
=
2T
M
ω
0
c
=
v
0
c
ω
0
. (1.4.44)
Контур линии, описываемый выражением (1.4.43), называют доплеровским. Полуширина (ширина на по-
ловине высоты) доплеровской линии δ равна
δ
D
=2
√
ln 2 ∆ω
D
. (1.4.45)
Поскольку доплеровское и естественное уширение происходят одновременно и независимо, то резуль-
тирующий контур является сверткой лоренцовского и доплеровского контуров:
ε
v
(ω)=
γ
2π
ε
(ω − ω
0
−ω
0
v/c)
2
+ γ
2
/4
, (1.4.46)
64
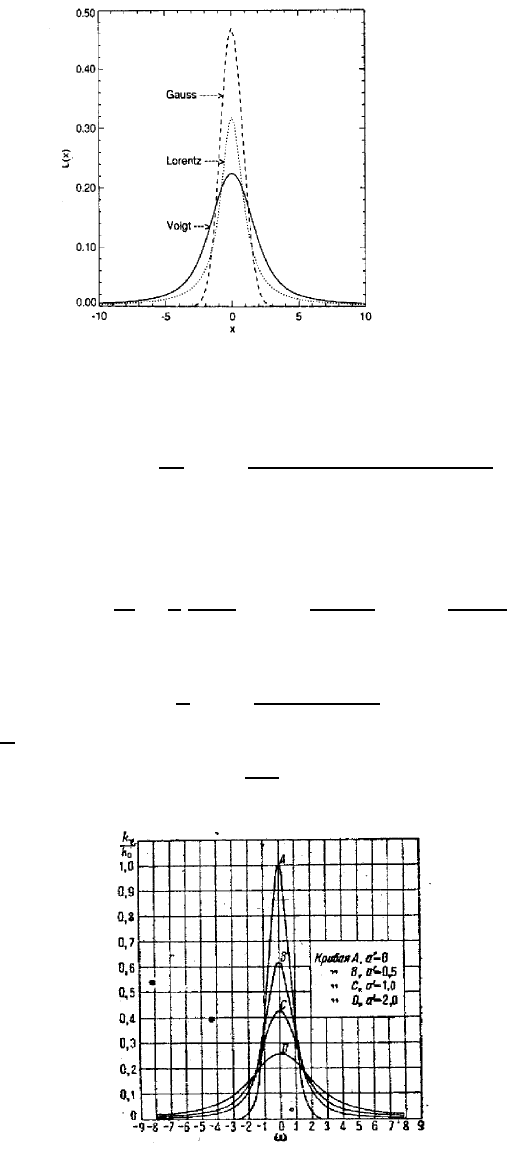
Рис. 25: Контуры линий лоренцевского, доплеровского и фойгтовского профилей [31].
ε(ω)=
γ
2π
+∞
−∞
ε
0
dp(v)
(ω − ω
0
− ω
0
v/c)
2
+Γ
2
/4
. (1.4.47)
Это выражение справедливо для любого распределения p(v). Если распределение максвелловское, то ис-
пользуя стандартные обозначения [29]
y =
v
v
0
=
v
c
ω
0
∆ω
D
,u=
ω − ω
0
∆ω
D
,a=
γ
2∆ω
D
,
получим
ε(ω)=ε
0
a
π
+∞
−∞
e
−y
2
dy
(u − y)
2
+ a
2
= ε
0
H(a, u) .
Здесь ε
0
=1/
√
π∆ω
D
– интенсивность в максимуме линии, а H(a, u) – функция Фойгта. Ее вид в
зависимости от величины a
=(∆ω
L
/∆ω
D
)
√
ln 2 показан на рис. 26.
Рис. 26: Лоренцевское уширение доплеровской линии [32], стр.145.
Коэффициент поглощения линии с фойгтовский контуром равен
k
ω
= k
0
H(a, u) , (1.4.48)
65

k
0
=
2π
2
e
2
mc
n
k
f
km
√
π∆ω
D
. (1.4.49)
В центре линии при любом a
ε(ω
0
)=ε
0
H(a, 0) = exp(a
2
) · erfc(a), (1.4.50)
где
erfc(a)=
2
√
π
∞
a
e
−x
2
dx (1.4.51)
– интеграл ошибок.
В предельном случае a<<1, когда доплеровское уширение много больше естественного, в центральной
части линии контур становится чисто доплеровским. На далеких крыльях линии (см. рис. 25), однако, контур
всегда остается дисперсионным.
1.4.5. Уширение давлением
Уширение спектральных линий, связанное с взаимодействием излучающей атомной системы с окружающей
средой, носит общее название “уширение давлением”. При сближении с другими частицами происходит
изменение силового поля в окрестности возбужденного атома, а следовательно, происходит изменение энер-
гии электронных термов. С современным уровнем квантово-механической теории уширения давлением и
основными экспериментальными результатами в этой области можно познакомиться в монографии [30]. Из
доступных книг можно порекомендовать [23, 24, 29, 31, 32, 33, 34, 35]. В данном параграфе мы очень
сжато изложим основные понятия теории уширения давлением в объеме, минимально необходимом для по-
нимания процессов в низкотемпературной плазме, исходя из простейшей теории возмущения классического
осциллятора окружающими частицами (см. [23, 24, 29, 35]).
В большинстве случаев в низкотемпературной плазме основную роль играют парные столкновения. Га-
мильтониан атома изменяется при столкновении на величину
V (R)=−
C
n
R
n
, (1.4.52)
где C
n
- константа, а n - целое число, зависящее от вида взаимодействия. В квазиклассическом прибли-
жении (считаем возмущение адиабатическим, то есть не приводящим к переходам между состояниями, а
траекторию прямолинейной) на атом накладывается внешнее поле
V (R)=V (
ρ
2
+ v
2
t
2
) , (1.4.53)
где t =0– момент наибольшего сближения, а v – относительная скорость. Сдвиг частоты перехода при
этом равен
∆ω (t)=C
n
(ρ
2
+ v
2
t
2
)
−n/2
, (1.4.54)
66

где n =2для линейного и n =4для квадратичного штарк-эффекта.
Предположим сначала, что продолжительность соударения мала по сравнению с временем между со-
ударениями (“ударное приближение” Лорентца, Ленца, Ландхольма). Тогда контур линии, излучаемой со-
ставной системой “возмущающиая частица+излучающий атом”, имеет вид
I(ω)=
Nvσ
π
1
(ω − ω
0
− Nvσ
)
2
+(Nvσ
)
2
, (1.4.55)
где сечения, определяющие уширение и сдвиг линии,
σ
=2π
∞
0
[1 − cos η(ρ)] ρdρ,
σ
=2π
∞
0
sin η(ρ) ρdρ
зависят от полного сдвига фазы колебаний осциллятора за время столкновения
η(ρ)=
∞
0
∆ω(R(t)) dt = α
C
n
vρ
n−1
.
Контур при ударном уширении (1.4.55), подобно естественному контуру, имеет дисперсионный вид.
Выражения для вычисления уширения γ ≡ Nvσ
исдвига∆ ≡ Nvσ
для линейного эффекта Штарка
(n=2), резонансного уширения при взаимодействии атомов одного и того же элемента (n=3), квадратич-
ного эффекта Штарка (n=4) и уширения Ван-дер-Ваальса (n=6) приведены, например, в [29, 34]. Для
оценок естественно считать “сильными” столкновения, для которых η ∼ 1. Это соответствует пролетам с
прицельным параметром, меньшим так называемого “радиуса Вайскопфа”
ρ
B
=(α
n
C
n
/v)
1/n−1
, (1.4.56)
где α
n
≤ 2 (см. [34]). Отсюда частота уширяющих столкнований
γ ∼ Nvπρ
2
b
. (1.4.57)
Характерное время столкновения равно τ
c
∼ ρ
B
/v, а соответствующая частота Ω
B
=1/τ
c
называ-
ется вайскопфовской. В согласии с принципом Месси контур (1.4.55) правильно описывает форму линии
при условии ∆ωτ
c
1. Центральную часть линии, удовлетворяющую условию ∆ω Ω
B
, называ-
ют ударной. Ее ширина может превосходить естественную ширину на много порядков. В обратном случае
∆ωτ
c
1 атом находится в поле действия других частиц, которое меняется достаточно медленно по срав-
нению со временем спонтанного излучения. В этом случае справедливо “статическое” (“квазистатическое”,
“статистическое”) приближение . Для вычисления контура линии достаточно найти плотность распределе-
ния осцилляторов по частотам. Будем считать, что основное поле создает ближайшая частица (приближение
“ближайшего соседа”). Вероятность нахождения ближайшей частицы на расстоянии R, R + dR равна
W (R)dR =4πR
2
N exp [−(4π/3)NR
3
] dR =exp[−(R/R
0
)
3
] d(R/R
0
) , (1.4.58)
67

где R
0
=(3/4πN)
1/3
.Введя∆¯ω = C
n
/R
n
0
,получим
I(ω)dω =
4πNC
3/n
n
n(ω − ω
0
)
(3+n)/n
exp
−
∆¯ω
ω − ω
0
3/n
dω . (1.4.59)
Выражение (1.4.59) имеет смысл только для достаточно больших значений (ω − ω
0
), для которых R =
[(ω − ω
0
)/C
n
]
−1/n
R
0
, и бинарное приближение справедливо.
Таким образом, центральная часть уширенной линии – лоренцовская, тогда как для больших значений
∆ω Ω
B
она описывается статическим контуром. Статическое крыло может располагаться как с длинно-
волновой, так и с коротковолновой стороны линии в зависимости от направления сдвига термов. В области
частот, противоположных по знаку статическому крылу, лоренцовское распределение сменяется экспонен-
циальным [34, c. 257].
Если бинарное приближение h = Nρ
3
0
1 становится несправедливым, то при h 1 статиче-
ская теория должна учитывать многочастичные взаимодействия. Такая теория была создана Хольцмарком
(см. [34]). Распределение Хольцмарка совпадает в асимптотике с выражением (1.4.59). Напомним, однако,
что более полно уширение давлением описывает не рассматривавшаяся здесь квановомеханическая теория.
1.4.6. Возбуждение и тушение электронных состояний
При столкновении атома, находящегося в некотором состоянии k, с электроном он может перейти в другое,
более высокое возбужденное состояние n.
A
k
+ e
k
kn
k
nk
A
n
+ e. (1.4.60)
Рис. 27: Сечение возбуждения разных уровней He .
Вероятность перехода k → n:
w
kn
= n
e
vσ
kn
= n
e
∞
√
2∆E
kn
/m
4πv
3
σ
kn
(v)f(v)dv = n
e
∞
∆E
kn
2E
m
σ
kn
(E)
√
Ef(E)dE,
(1.4.61)
68

Рис. 28: Вероятности возбуждения и ионизации вблизи атомов порога.
Обратный процесс безизлучательного перехода при столкновении с электроном называют “тушением” или
дезактивацией. Этот процесс – беспороговый. Скорость обратного процесса можно найти из принципа де-
тального равновесия
n
0
k
w
kn
= n
0
n
w
nk
. (1.4.62)
Характерный вид зависимости сечения возбуждения разных состояний в зависимости от энергии на-
летающих электронов в сравнении с сечениями ионизации и уругого рассеяния приведен на рис. 27. Се-
чение резко растет после достижения порога реакции, а затем медленно спадает. При больших энергиях
(E >> ∆E
kn
) для оптически разрешенных переходов сечение аппроксимируется выражением
σ
kn
(E) ∼
ln E
E
, (1.4.63)
тогда как для запрещенных переходов зависимость имеет вид [35, 36]
σ
kn
(E) ∼
1
E
. (1.4.64)
В низкотемпературной плазме температура электронов много меньше потенциалов возбуждения, и только
хвосты функции распределения электронов участвуют в процессе возбуждения атомов. Понятно, что ма-
кроскопическая скорость реакции существенным образом определяется как видом функции распределения,
так и видом зависимости сечения возбуждения вблизи порога от энергии. Согласно теории, в борновском
приближении на пороге (E∼∆E
kn
) зависимость от энергии имеет вид
σ
kn
(E) ∼
E−∆E
kn
. (1.4.65)
Согласно экспериментальным данным, однако, эта зависимость скорее является линейно возрастающей
σ
kn
(E) ∼ a(E−∆E
kn
) . (1.4.66)
69
