Кирсанова О.В., Семёнова Г.А. Математическое программирование (типовой расчёт)
Подождите немного. Документ загружается.

60
Такой метод выгодно применять, когда первое базисное решение
прямой задачи недопустимое или, например, когда число еѐ ограни-
чений больше числа переменных, как и в нашем случае.
Таким образом, будем решать симплекс-методом двойственную
задачу. Внесѐм еѐ данные в симплекс-таблицу 42 (подробно метод
был описан в упражнении 2).
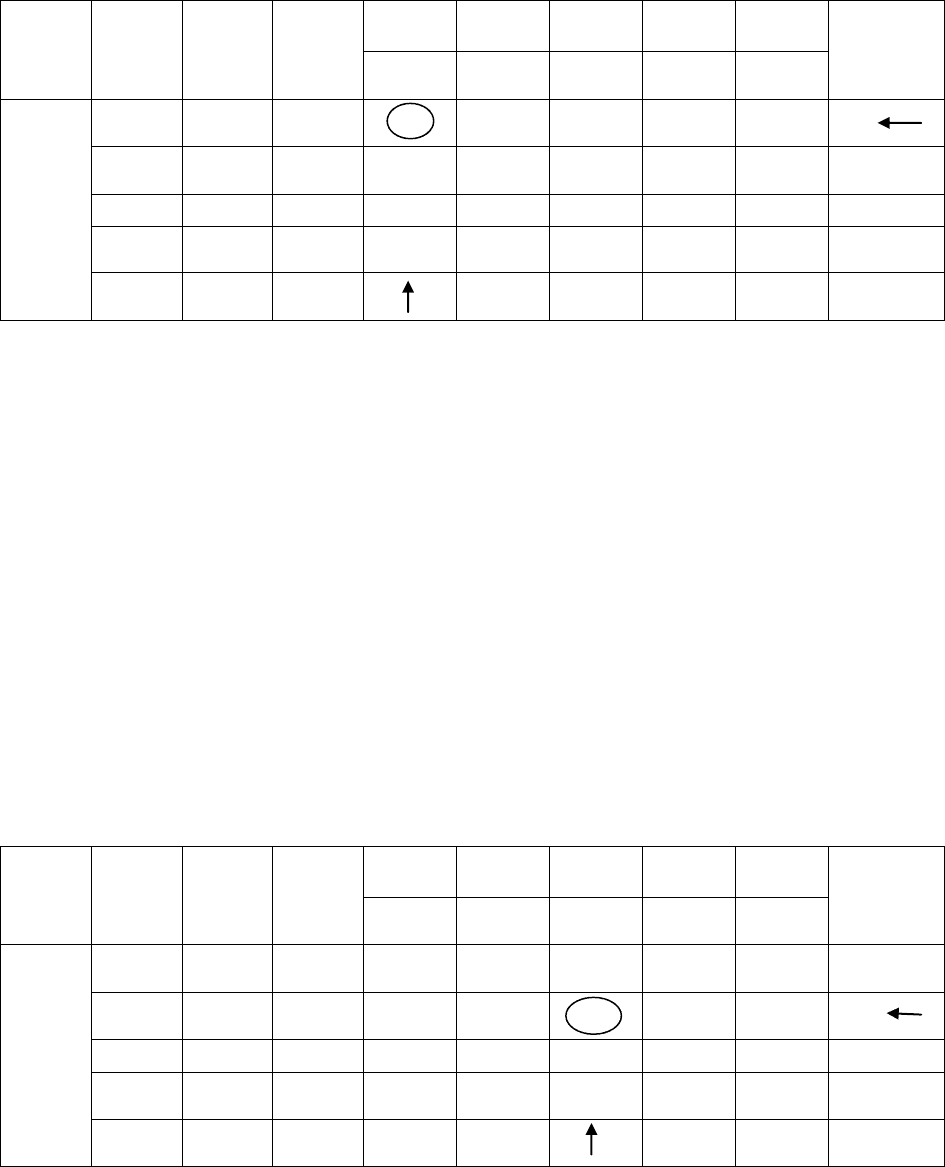
Таблица 42
План
Базис
С
б
b
i
16
11
10
0
0
d
i
y
1
y
2
y
3
y
4
y
5
I
y
4
0
1
3
3
1
1
0
1/3
y
5
0
2
2
1
3
0
1
1
Z
=
0
–16
–11
–10
0
0
Базисным решением на первом шаге будет Y
1
= (0; 0; 0; 1; 2), при
котором целевая функция будет Z равна 0, то есть Z
1
= 0.
Для базисного решения Y
1
критерий оптимальности не выполнен,
так как в столбцах, соответствующих свободным переменным y
1
, y
2
и
y
3
, в целевой функции есть отрицательные элементы (– 16, – 11
и – 10), выбираем из них наименьший.
Чтобы перейти к построению плана II, нужно перевести перемен-
ную y
1
в базис. Тогда столбец y
1
– разрешающий столбец. Заполняем
столбец оценочных отношений d
i
, и в качестве разрешающей строки
выбираем ту, которой соответствует базисная переменная y
4
(с наи-
меньшим элементом в столбце оценочных отношений), то есть базис-
ными в плане II будут y
1
, y
5
.
Вычисляем элементы новой симплекс-таблицы 43.
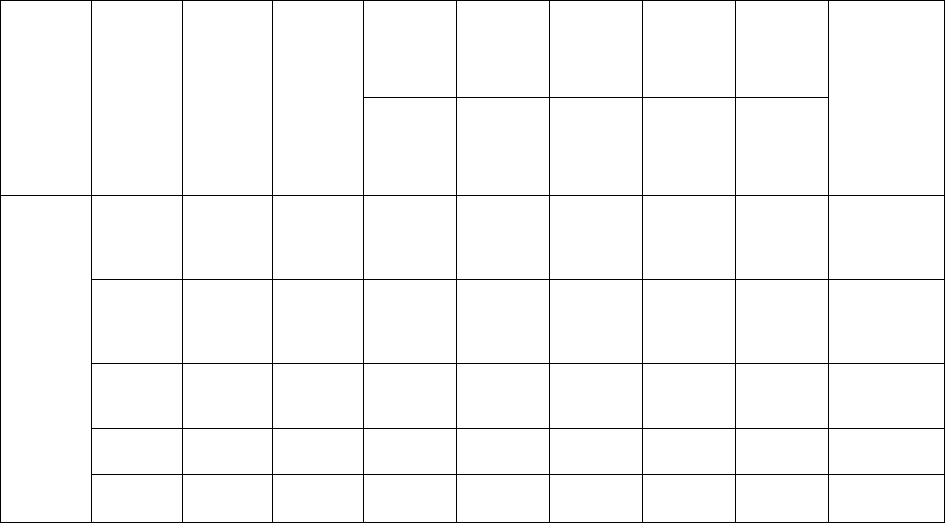
Таблица 43
План
Базис
С
б
b
i
16
11
10
0
0
d
i
y
1
y
2
y
3
y
4
y
5
II
y
1
16
1/3
1
1
1/3
1/3
0
1
y
5
0
4/3
0
–1
7/3
–2/3
1
4/7
Z
=
16/3
0
5
–14/3
16/3
0
61
Базисным решением на втором шаге будет Y
2
= (1/3; 0; 0; 0; 4/3),
при котором целевая функция будет Z равна 16/3, то есть Z
2
= 16/3.
Для базисного решения Y
2
критерий оптимальности не выполнен,
так как в столбце, соответствующем свободной переменной y
3
, в це-
левой функции отрицательный элемент (– 14/3).
Чтобы перейти к построению плана III, нужно перевести пере-
менную y
3
в базис. Тогда столбец y
3
– разрешающий столбец. Запол-
няем столбец оценочных отношений d
i
, и в качестве разрешающей
строки выбираем ту, которой соответствует базисная переменная y
5
(с
наименьшим элементом в столбце оценочных отношений), то есть ба-
зисными в плане III будут y
1
, y
3
.
Вычисляем элементы новой симплекс-таблицы 44.
Таблица 44
План
Базис
С
б
b
i
16
11
10
0
0
d
i
y
1
y
2
y
3
y
4
y
5
III
y
1
16
1/7
1
8/7
0
3/7
–1/7
y
3
10
4/7
0
–3/7
1
–2/7
3/7
Z
=
8
0
3
0
4
2
Базисным решением будет Y
3
= (1/7; 4/7; 0; 0; 0), при котором це-
левая функция будет Z равна 8, то есть Z
3
= 8.
Для базисного решения Y
3
выполнен критерий оптимальности,
так как в целевой функции нет отрицательных элементов. Кроме того,
все коэффициенты при свободных переменных (y
2
, y
4
, y
5
) отличны
от нуля, следовательно, полученное решение Y
3
оптимально и един-
ственно.
Таким образом, Y* = (1/7; 4/7; 0; 0; 0), Z
max
= 8.
Установим соответствие между переменными и найдем решение
прямой задачи (табл. 45).
62
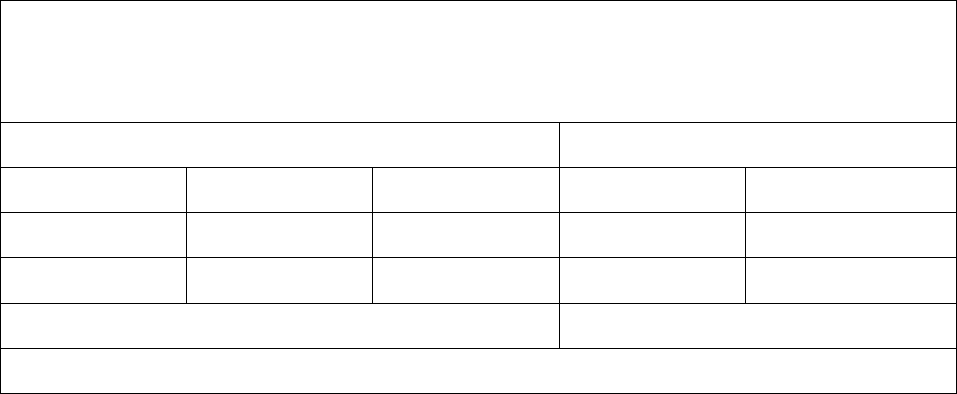
Таблица 45
Абсолютные значения коэффициентов
при переменных целевой функции двойственной задачи,
выраженной через свободные переменные еѐ оптимального решения
основные переменные
дополнительные переменные
y
1
y
2
y
3
y
4
y
5
0
3
0
4
2
x
3
x
4
x
5
x
1
x
2
дополнительные переменные
основные переменные
компоненты оптимального решения прямой задачи
X* = (4; 2; 0; 3; 0); F* = 8.
Контроль: F* = 1·4 + 2·2 = 8.
Ответ: X* = (4; 2; 0; 3; 0); F
min
= 8.
Y* = (1/7; 4/7; 0; 0; 0); Z
max
= 8.
Задача 7. Найдите решение задачи графически и двойственным
симплекс-методом.
7.1.
12
12
12
12
12
2 3 min;
6,
4 9,
3 10;
0, 0.
F x x
xx
xx
xx
xx
7.2.
12
12
12
12
12
3 2 min;
3 10,
4 15,
2 5 24;
0, 0.
F x x
xx
xx
xx
xx
7.3.
12
12
12
12
12
2 7 min;
5 2 24,
4 15,
5 14;
0, 0.
F x x
xx
xx
xx
xx
7.4.
12
12
12
12
12
2 min;
6 15,
7 20,
4 14;
0, 0.
F x x
xx
xx
xx
xx
7.5.
.0,0
,83
,103
,6
min,32
21
21
21
21
21
xx
xx
xx
xx
xxF
7.6.
12
12
12
12
12
3 min;
7,
5 15,
2 9;
0, 0.
F x x
xx
xx
xx
xx
63
7.7.
12
12
12
12
12
5 2 min;
3 9,
5 12,
2 5 19;
0, 0.
F x x
xx
xx
xx
xx
7.8.
12
12
12
12
12
2 5 min;
3 2 12,
4 12,
3 11;
0, 0.
F x x
xx
xx
xx
xx
7.9.
12
12
12
12
12
3 min;
3 14,
7 6 62,
4 12;
0, 0.
F x x
xx
xx
xx
xx
7.10.
12
12
12
12
12
3 4 min;
3 11,
7 6 55,
4 11;
0, 0.
F x x
xx
xx
xx
xx
7.11.
12
12
12
12
12
2 3 min;
3 12,
4 3 26,
2 9;
0, 0.
F x x
xx
xx
xx
xx
7.12.
12
12
12
12
12
3 4 min;
3 10,
5 17,
2 5 24;
0, 0.
F x x
xx
xx
xx
xx
7.13.
12
12
12
12
12
2 min;
3 5,
11,
5 23;
0, 0.
F x x
xx
xx
xx
xx
7.14.
12
12
12
12
12
3 2 min;
4 10,
7,
2 2;
0, 0.
F x x
xx
xx
xx
xx
7.15.
.0,0
,1832
,142
,22
min,4
21
21
21
21
21
xx
xx
xx
xx
xxF
7.16.
12
12
12
12
12
2 3 min;
5 22,
3 2,
2 5 18;
0, 0.
F x x
xx
xx
xx
xx
7.17.
12
12
12
12
12
4 3 min;
5 2,
2 12,
4 13;
0, 0.
F x x
xx
xx
xx
xx
7.18.
12
12
12
12
12
3 2 min;
5 2 24,
6 5 47,
3 10;
0, 0.
F x x
xx
xx
xx
xx
64
7.19.
12
12
12
12
12
3 4 min;
2 10,
2 11,
5 14;
0, 0.
F x x
xx
xx
xx
xx
7.20.
12
12
12
12
12
4 3 min;
3 9,
7,
2 8;
0, 0.
F x x
xx
xx
xx
xx
7.21.
12
12
12
12
12
2 min;
4 4,
3 14,
2 1;
0, 0.
F x x
xx
xx
xx
xx
7.22.
12
12
12
2
12
4 min;
3 2 14,
3 14,
1;
0, 0.
F x x
xx
xx
x
xx
7.23.
12
12
12
12
12
3 2 min;
2 6,
5,
2 6;
0, 0.
F x x
xx
xx
xx
xx
7.24.
12
12
12
12
12
3 4 min;
2 7,
4 19,
1;
0, 0.
F x x
xx
xx
xx
xx
7.25.
12
12
12
12
12
3 min;
6,
2 10,
4 12;
0, 0.
F x x
xx
xx
xx
xx
7.26.
12
12
12
12
12
2 min;
4 9,
2 7,
3 6;
0, 0.
F x x
xx
xx
xx
xx
7.27
12
12
12
12
12
2 5 min;
3 2 19,
2 3 21,
4 13;
0, 0.
F x x
xx
xx
xx
xx
7.28
12
12
12
12
12
4 3 min;
3 13,
6 7 61,
2 11;
0, 0.
F x x
xx
xx
xx
xx
7.29.
12
12
12
12
12
5 2 min;
5 18,
7 5 54,
2 9;
0, 0.
F x x
xx
xx
xx
xx
7.30.
12
12
12
12
12
3 2 min;
3 8,
2 3 17,
5 12;
0, 0.
F x x
xx
xx
xx
xx
7.31.
12
12
12
12
12
2 min;
3 2 16,
3 11,
3 10;
0, 0.
F x x
xx
xx
xx
xx
65
ГЛАВА 2. ТРАНСПОРТНАЯ ЗАДАЧА
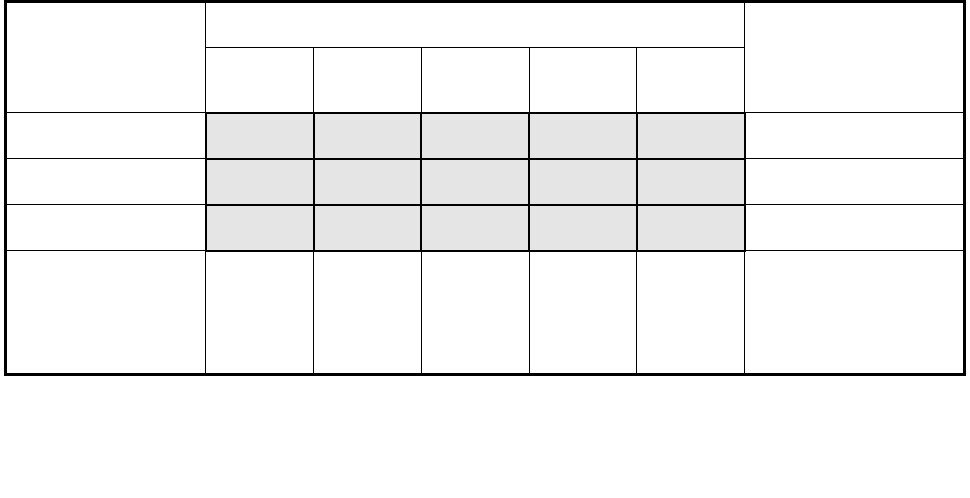
Упражнение 1. Получите опорный план транспортной задачи
(табл. 46) тремя методами. Оптимизируйте план, полученный мето-
дом наименьших затрат.
Таблица 46
Поставщики
(пункты
отправки)
Потребители (пункты назначения)
Запасы
товара, a
i
В
1
В
2
В
3
В
4
В
5
А
1
18
26
16
22
9
200
А
2
7
12
19
23
15
300
А
3
10
8
17
19
14
200
Спрос
на товар, b
j
120
110
80
200
190
700
Решение.
700200300200
i
a
,
70019020080110120
j
b
.
Так как
ji
ba
, то имеем закрытую транспортную задачу,
n = 3, m = 5.
1-й метод. Метод «северо-западного угла»
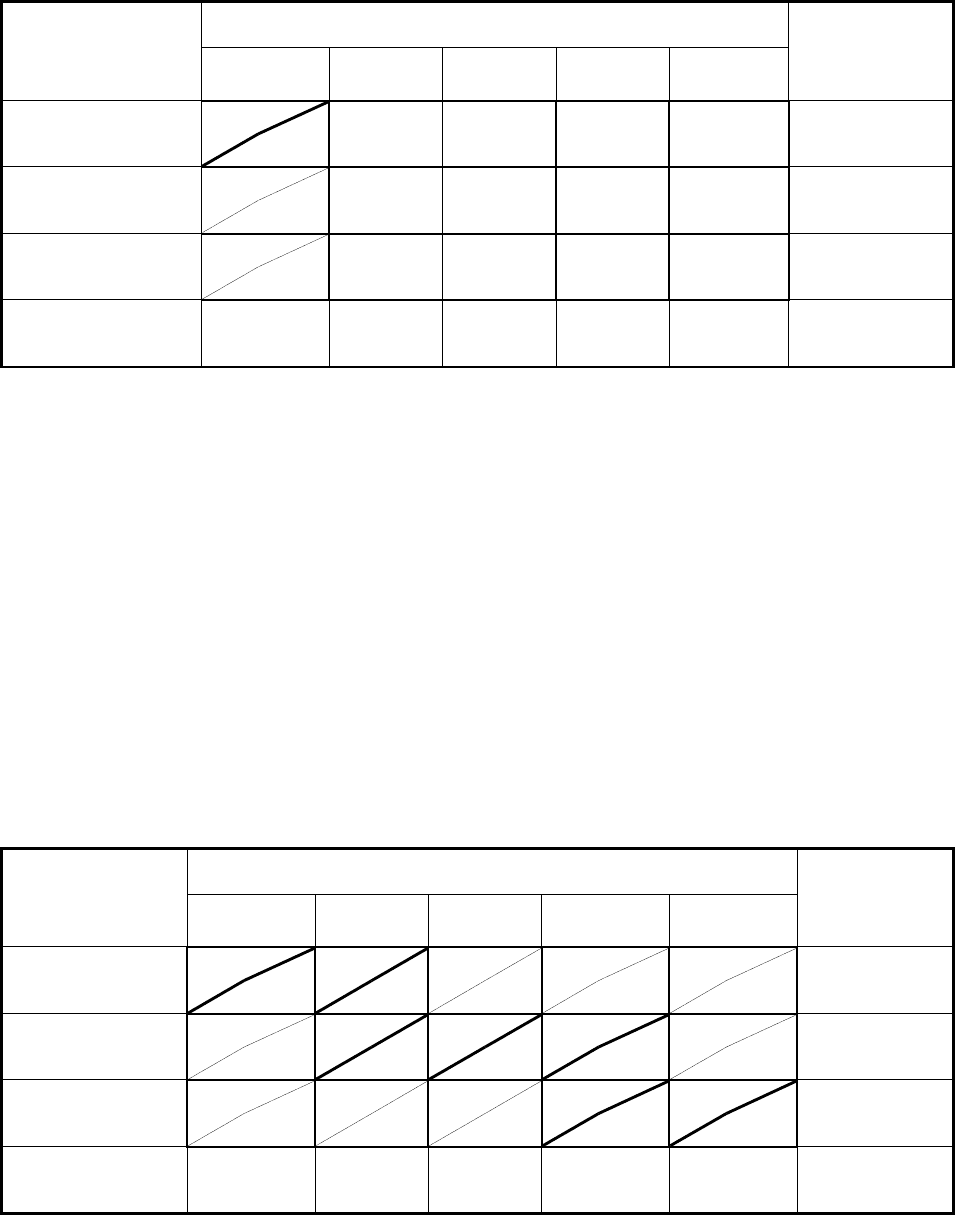
Таблица 47 заполняется, начиная с «северо-западного» угла, то
есть с левой верхней клетки.
Дадим переменной x
11
максимально возможное значение или,
иными словами, максимально возможную поставку в клетку (1; 1) –
«северо-западный» угол таблицы поставок: x
11
= min{200, 120} = 120.
После этого спрос первого потребителя полностью удовлетворѐн, в
результате чего первый столбец таблицы поставок исключается из
дальнейшего рассмотрения (до тех пор, пока опорный план не будет
составлен полностью). Заполненные клетки будем перечѐркивать по
диагонали сплошной линией, а исключѐнные из дальнейшего рас-
смотрения – пунктирной линией; при этом предложение первого по-
ставщика уменьшается на 120 ед. и составит 80 ед.
66
Таблица 47
Поставщики
(пункты
отправки)
Потребители (пункты назначения)
Запасы
товара, a
i
В
1
В
2
В
3
В
4
В
5
А
1
18
26
16
22
9
200/ 80
120
А
2
7
12
19
23
15
300
А
3
10
8
17
19
14
200
Спрос
на товар, b
j
120/ –
110
80
200
190
700
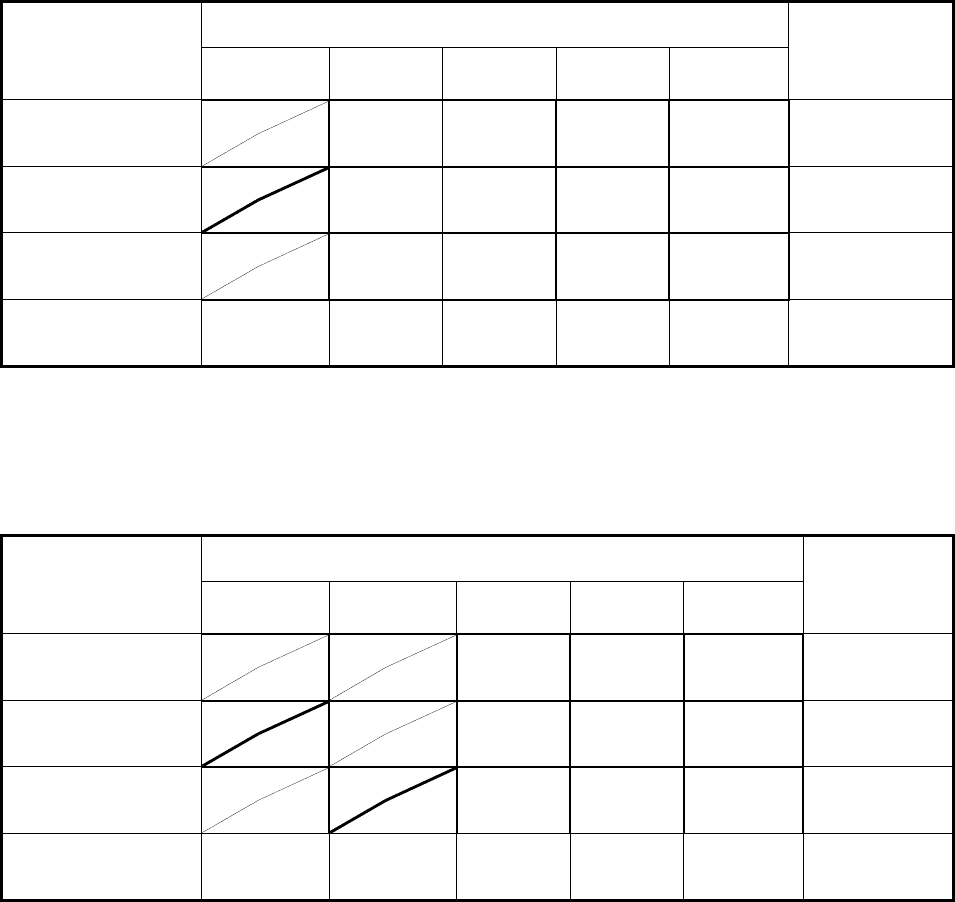
Теперь в таблице поставок 48 находим новый «северо-западный»
угол – клетку (1; 2) и отправляем в неѐ максимально возможную по-
ставку x
12
= min{80, 110} = 80, клетка (1; 2) перечѐркивается сплош-
ной линией. После этого мощность первого поставщика полностью
использована, то есть клетки (1; 3), (1; 4) и (1; 5) исключаются из рас-
смотрения и перечѐркиваются пунктиром. В оставшейся таблице
вновь находим «северо-западный» угол и отправляем туда макси-
мально возможную поставку. И так далее.
В результате получаем опорный план, в котором заполненными
(базисными) являются n + m – 1 = 5 + 3 – 1 = 7 клеток.
Таблица 48
Поставщики
(пункты
отправки)
Потребители (пункты назначения)
Запасы
товара, a
i
В
1
В
2
В
3
В
4
В
5
А
1
18
26
16
22
9
200/ 80/ –
120
80
А
2
7
12
19
23
15
300/ 270/
190/ –
30
80
190
А
3
10
8
17
19
14
200/ 190/ –
10
190
Спрос
на товар, b
j
120/ –
110/
30/ –
80/ –
200/
10/ –
190/ –
700
Этому плану соответствует значение целевой функции
F
сз
= 18·120 + 26·80 + 12·30 + 19·80 + 23·190 + 19·10 + 14·190 = 13340
.
2-й метод. Метод наименьших затрат
67
Согласно этому методу, на каждом шаге заполняется клетка с ми-
нимальным коэффициентом затрат.
В табл. поставок 49 находим клетку с наименьшим коэффициен-
том затрат. Это клетка (2; 1) с коэффициентом затрат равным 7 (если
таких клеток несколько, то выбираем ту, в которую возможна макси-
мальная поставка), причѐм x
21
= min{300, 120} = 120.
Таблица 49
Поставщики
(пункты от-
правки)
Потребители (пункты назначения)
Запасы
товара, a
i
В
1
В
2
В
3
В
4
В
5
А
1
18
26
16
22
9
200
А
2
7
12
19
23
15
300/ 180
120
А
3
10
8
17
19
14
200
Спрос
на товар, b
j
120/ –
110
80
200
190
700
Тогда спрос первого потребителя полностью удовлетворѐн, и пер-
вый столбец исключѐн из рассмотрения.
Таблица 50
Поставщики
(пункты
отправки)
Потребители (пункты назначения)
Запасы
товара, a
i
В
1
В
2
В
3
В
4
В
5
А
1
18
26
16
22
9
200
А
2
7
12
19
23
15
300/ 180
120
А
3
10
8
17
19
14
200/ 90
110
Спрос
на товар, b
j
120/ –
110/ –
80
200
190
700
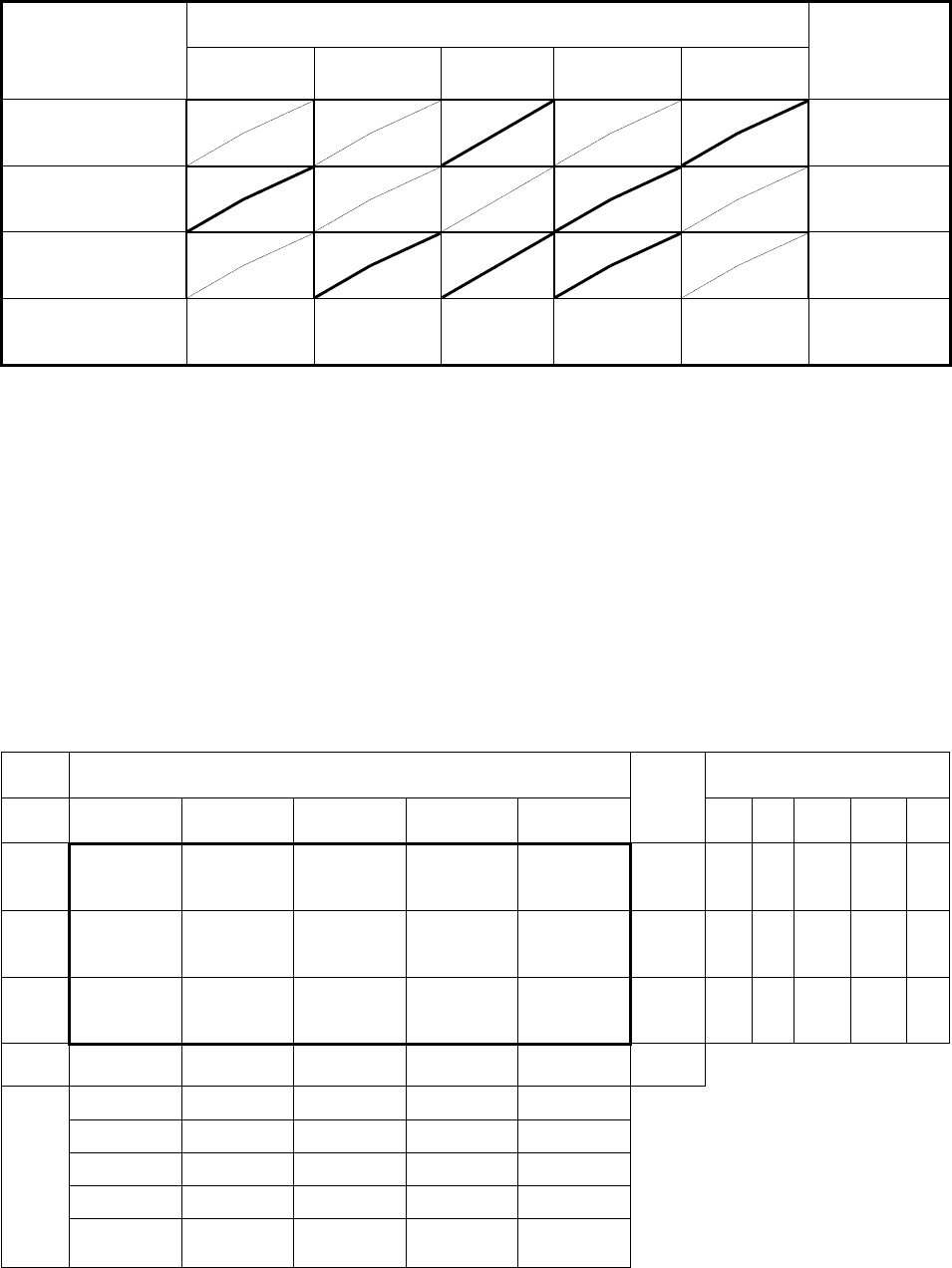
В оставшейся табл. 50 наименьший коэффициент затрат равен 8 и
находится в клетке (3; 2), x
32
= min{200, 110} = 110. При этом из рас-
смотрения выбывает второй столбец.
Продолжая заполнение таблицы шаг за шагом (табл. 51),
получаем x
15
= min{200, 190} = 190, x
13
= min{10, 80} = 10,
x
33
= min{90, 70} = 70, x
34
= min{20, 180} = 20, x
24
= 180. В результате
68
получаем опорный план, в котором заполненными (базисными) яв-
ляются 7 клеток.
Таблица 51
Поставщики
(пункты
отправки)
Потребители (пункты назначения)
Запасы
товара, a
i
В
1
В
2
В
3
В
4
В
5
А
1
18
26
16
22
9
200/ 10/ –
10
190
А
2
7
12
19
23
15
300/ 180/
–
120
180
А
3
10
8
17
19
14
200/ 90/
20
110
70
20
Спрос
на товар, b
j
120/ –
110/ –
80/ 70/
–
200/
180/ –
190/ –
700
Соответствующее значение целевой функции равно
F
нз
= 16·10 + 9·190 + 7·120 + 23·180 + 8·110 + 17·70 + 19·20 = 9300.
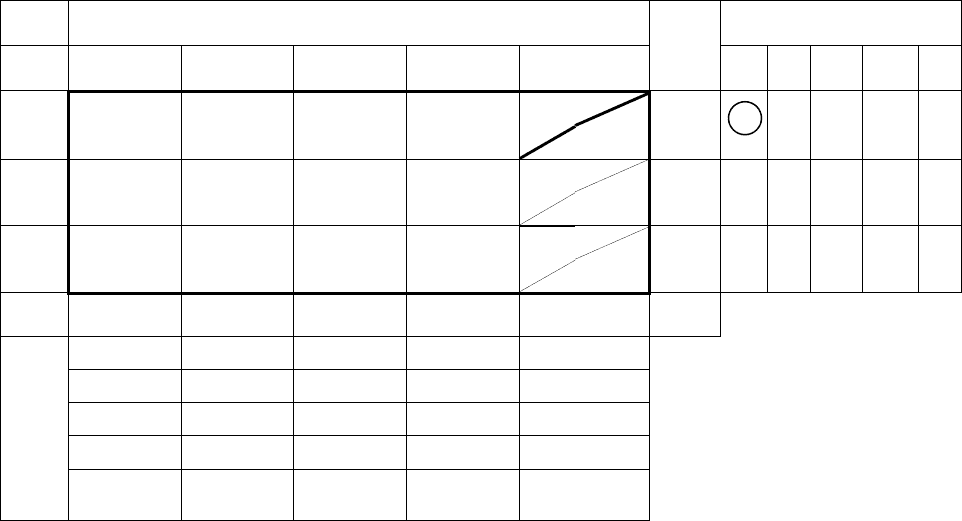
3-й метод. Метод аппроксимации Фогеля
При определении опорного плана транспортной задачи методом
аппроксимации Фогеля, на каждой итерации по всем строкам и всем
столбцам находим разность между двумя минимальными коэффици-
ентами затрат. Эти разности записываем в специально отведѐнные
для этого строку и столбец табл. поставок 52.
Таблица 52
Пункты назначения
a
i
Разности по строкам
ПО
В
1
В
2
В
3
В
4
В
5
I
II
III
IV
V
А
1
18
26
16
22
9
200
А
2
7
12
19
23
15
300
А
3
10
8
17
19
14
200
b
j
120
110
80
200
190
700
Разности
по столбцам
69
Среди полученных разностей выбираем максимальную. В строке
(или столбце), которой данная разность соответствует, заполняем
клетку с минимальным коэффициентом затрат.
Если минимальный коэффициент затрат одинаков для нескольких
клеток выбранной строки (столбца), то для заполнения выбираем ту
клетку, которая расположена в столбце (строке) с максимальной раз-
ностью по столбцам (строкам).
Первый этап. Для каждой строки и каждого столбца вычисляем
разности между минимальными коэффициентами затрат (табл. 53).
Таблица 53
Пункты назначения
a
i
Разности по строкам
ПО
В
1
В
2
В
3
В
4
В
5
I
II
III
IV
V
А
1
18
26
16
22
9
200/
10
7
190
А
2
7
12
19
23
15
300
5
А
3
10
8
17
19
14
200
2
b
j
120
110
80
200
190/ –
700
Разности по
столбцам
3
4
1
3
5
В строке А
1
минимальный коэффициент затрат равен 9, а сле-
дующий за ним равен 16, разность между ними 16 – 9 = 7. В строке А
2
разность равна 12 – 7 = 5, и так далее. Вычислив все разности, видим,
что наибольшая из них соответствует строке А
1
. В этой строке мини-
мальный коэффициент затрат находится в клетке (1; 5) и равен 9.
Отправим в эту клетку максимально возможную поставку
x
15
= min{200, 190} = 190. При этом потребности пятого потребителя
полностью удовлетворены, и он исключается из рассмотрения, а за-
пасы пункта А
1
равны 200 – 190 = 10.
Второй этап. Снова вычисляем разности между минимальными
коэффициентами затрат (табл. 54) и видим, что наибольшая из них
соответствует строке А
2
. В этой строке минимальный коэффициент
затрат находится в клетке (2; 1) и равен 7. Отправим в эту клетку
максимально возможную поставку x
21
= min{300, 120} = 120.
