Кирсанова О.В., Семёнова Г.А. Математическое программирование (типовой расчёт)
Подождите немного. Документ загружается.

30
Y* = (0; 17/14; 1/14; 0; 0; 0); Z* = F* = –35.
Контроль: Z* = –4 · 0 – 27·17/14 – 31·1/14 – 2·0 = –35.
Ответ: X* = (5; 8; 11; 0; 0; 5); F
min
= –35.
Y* = (0; 17/14; 1/14; 0; 0; 0 ); Z
max
= –35.
Задача 2. Найдите решение задачи симплексным методом, про-
иллюстрировав его графически. Составьте двойственную задачу и на
основании теорем двойственности сделайте вывод о ее решении.
2.1.
12
12
12
12
12
12
4 min;
5 3,
2 5 42,
3 12,
2;
0, 0.
F x x
xx
xx
xx
xx
xx
2.2.
12
12
12
12
12
12
5 min;
4 4,
4 31,
4 29,
1;
0, 0.
F x x
xx
xx
xx
xx
xx
2.3.
12
12
12
12
12
12
2 3 min;
2 2,
3,
3 2 26,
4 3 12;
0, 0.
F x x
xx
xx
xx
xx
xx
2.4.
12
12
12
12
12
12
6 min;
4 1,
7 34,
5 34,
2 5;
0, 0.
F x x
xx
xx
xx
xx
xx
2.5.
12
12
12
12
12
12
2 7 min;
3 2 6,
2 5 26,
4 36,
2 3 4;
0, 0.
F x x
xx
xx
xx
xx
xx
2.6.
12
12
12
12
12
12
8 min;
5 2 2,
7 40,
6 47,
3 5;
0, 0.
F x x
xx
xx
xx
xx
xx
2.7.
12
12
12
12
12
12
5 min;
3 2 8,
2 16,
4 19,
4 1;
0, 0.
F x x
xx
xx
xx
xx
xx
2.8.
12
12
12
12
12
12
6 min;
5 2,
4 27,
2 18,
3;
0, 0.
F x x
xx
xx
xx
xx
xx
31
2.9.
12
12
12
12
12
12
2 7 min;
5 2 4,
2 5 31,
7 2 67,
3 3;
0, 0.
F x x
xx
xx
xx
xx
xx
2.10.
12
12
12
12
12
12
2 3 min;
3 1,
3,
3 19,
4 2;
0, 0.
F x x
xx
xx
xx
xx
xx
2.11.
12
12
12
12
12
12
5 2 min;
3 2,
2 18,
2 11,
5;
0, 0.
F x x
xx
xx
xx
xx
xx
2.12.
12
12
12
12
12
12
7 2 min;
5 2 6,
4 34,
3 11,
2 2;
0, 0.
F x x
xx
xx
xx
xx
xx
2.13.
12
12
12
12
12
12
7 3 min;
2 1,
2 9 41,
2 15,
4 4;
0, 0.
F x x
xx
xx
xx
xx
xx
2.14.
12
12
12
12
12
12
3 min;
4 2,
2 5 28,
5 38,
4;
0, 0.
F x x
xx
xx
xx
xx
xx
2.15.
12
12
12
12
12
12
4 min;
5 4,
6 55,
3 13,
2 1;
0, 0.
F x x
xx
xx
xx
xx
xx
2.16.
12
12
12
12
12
12
2 5 min;
5 1,
3 5 27,
8 39,
3 2;
0, 0.
F x x
xx
xx
xx
xx
xx
2.17.
12
12
12
12
12
12
2 min;
3 2 4,
6 32,
3 2 16,
2 4;
0, 0.
F x x
xx
xx
xx
xx
xx
2.18.
12
12
12
12
12
12
2 7 min;
3 2 4,
3 8 34,
7 2 54,
5 3;
0, 0.
F x x
xx
xx
xx
xx
xx
32
2.19.
12
12
12
12
12
12
5 2 min;
4 3 6,
2 7 36,
2 12,
2 3;
0, 0.
F x x
xx
xx
xx
xx
xx
2.20.
12
12
12
12
12
12
3 min;
3 2 2,
2 10,
7 50,
3 4;
0, 0.
F x x
xx
xx
xx
xx
xx
2.21.
12
12
12
12
12
12
9 2 min;
2 4,
4 23,
3 19,
2 3 8;
0, 0.
F x x
xx
xx
xx
xx
xx
2.22.
12
12
12
12
12
12
5 min;
2,
3 12,
4 30,
2 3 8;
0, 0.
F x x
xx
xx
xx
xx
xx
2.23.
12
12
12
12
12
12
4 min;
3 3,
2 13,
3 11,
3 1;
0, 0.
F x x
xx
xx
xx
xx
xx
2.24.
12
12
12
12
12
12
6 min;
3 1,
5 33,
5 27,
3 4 6;
0, 0.
F x x
xx
xx
xx
xx
xx
2.25.
12
12
12
12
12
12
5 min;
3 1,
2 5 18,
4 30,
2 3;
0, 0.
F x x
xx
xx
xx
xx
xx
2.26.
12
12
12
12
12
12
2 5 min;
4 3,
2 13,
3 24,
2 6;
0, 0.
F x x
xx
xx
xx
xx
xx
2.27.
12
12
12
12
12
12
4 min;
2 3,
2 5 39,
3 16,
2 3 6;
0, 0.
F x x
xx
xx
xx
xx
xx
2.28.
12
12
12
12
12
12
3 min;
3,
2 8,
5 3 64,
2 5;
0, 0.
F x x
xx
xx
xx
xx
xx

33
2.29.
12
12
12
12
12
12
4 min;
1,
3 5 11,
6 41,
3 4;
0, 0.
F x x
xx
xx
xx
xx
xx
2.30.
12
12
12
12
12
12
5 3 min;
4,
2 20,
3 2 20,
2 4;
0, 0.
F x x
xx
xx
xx
xx
xx
2.31.
12
12
12
12
12
12
5 min;
3 4,
4 27,
3 2 31,
2;
0, 0.
F x x
xx
xx
xx
xx
xx
Упражнение 3. Найдите решение задачи симплексным методом,
проиллюстрировав его графически. Составьте двойственную
задачу и, на основании теорем двойственности, сделайте вывод
о ее решении.
.0,0
,162
,183
max,2
21
21
21
21
xx
xx
xx
xxF
Решение.
Решим задачу симплекс-методом (подробно этот метод был опи-
сан в упражнении 2). Для этого приведем задачу к каноническому
виду:
.0,0,0,0
,162
,183
max,2
4321
421
321
21
xxxx
xxx
xxx
xxF
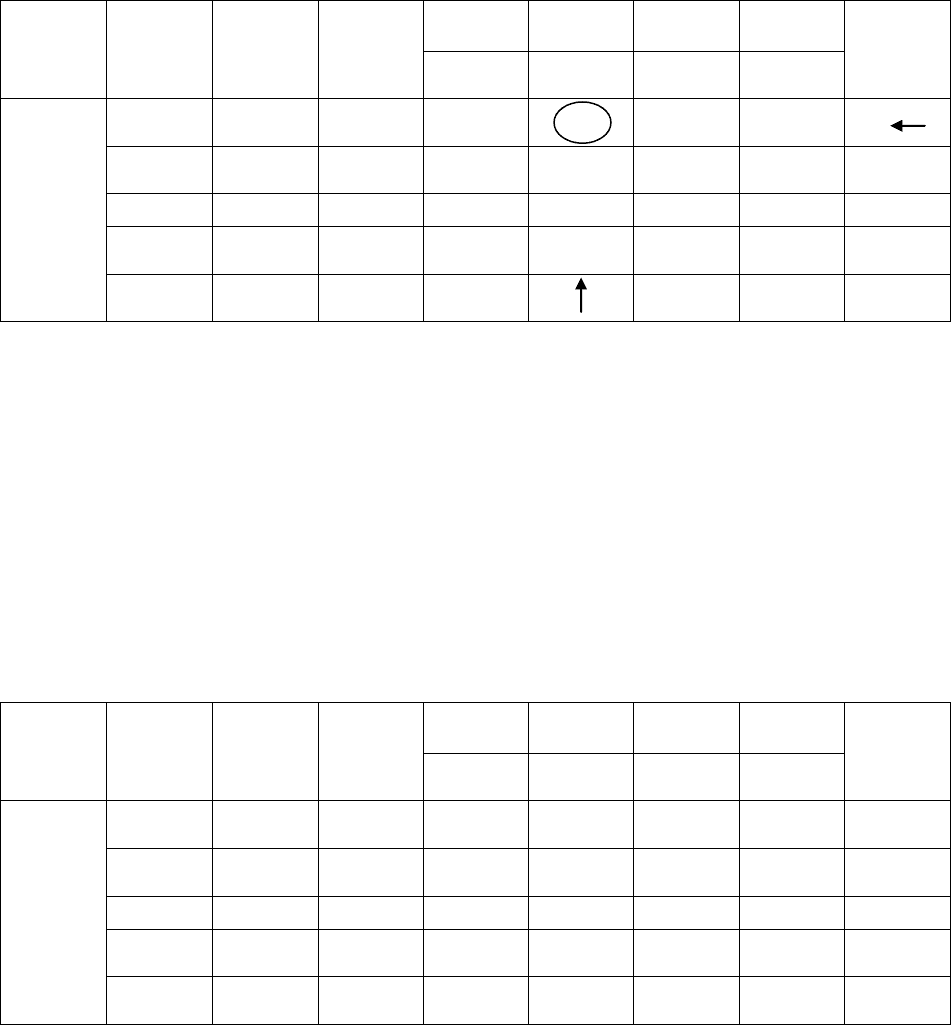
Внесѐм данные задачи в симплекс-таблицу 29.
Таблица 29
План
Базис
С
б
b
i
2
1
0
0
d
i
x
1
x
2
x
3
x
4
I
x
3
0
18
1
3
1
0
18
x
4
0
16
2
1
0
1
8
F
=
0
–2
–1
0
0
Базисным решением на первом шаге будет X
1
= (0; 0; 18; 16) (точ-
ка X
1
(0; 0) рис. 3), при котором целевая функция будет F равна 0,
то есть F
1
= 0.
34
Для базисного решения X
1
критерий оптимальности не выполнен,
так как в столбцах, соответствующих свободным переменным x
1
и x
2
,
в целевой функции есть отрицательные элементы (–2 и –1); выбираем
из них наименьший.
Чтобы перейти к построению плана II, нужно перевести перемен-
ную x
1
в базис. Тогда столбец x
1
– разрешающий столбец. Заполняем
столбец оценочных отношений d
i
, и в качестве разрешающей строки
выбираем ту, которой соответствует базисная переменная x
4
(с наи-
меньшим элементом в столбце оценочных отношений), то есть базис-
ными в плане II будут x
1
, x
3
.
Вычисляем элементы новой симплекс-таблицы 30.
Таблица 30
План
Базис
С
б
b
i
2
1
0
0
d
i
x
1
x
2
x
3
x
4
II
x
3
0
10
0
5/2
1
–1/2
4
x
1
2
8
1
1/2
0
1/2
16
F
=
16
0
0
0
1
Базисным решением на втором шаге будет X
2
= (8; 0; 10; 0)
(точка X
2
(8; 0) рис. 3), при котором целевая функция будет F равна
16, то есть F
2
= 16.
Так как в F-строке II-го плана симплекс-таблицы все элементы
неотрицательны, то этот план является оптимальным. Но он не един-
ственный, так как в F-строке существует нулевой элемент, соответст-
вующий свободной переменной (в данном примере это x
2
).
Чтобы найти второй оптимальный план, x
2
-столбец примем за
разрешающий и перейдем к следующему плану (табл. 31).
Таблица 31
План
Базис
С
б
b
i
2
1
0
0
d
i
x
1
x
2
x
3
x
4
III
x
2
1
4
0
1
2/5
–1/5
x
1
2
6
1
0
–1/5
3/5
F
=
16
0
0
0
1
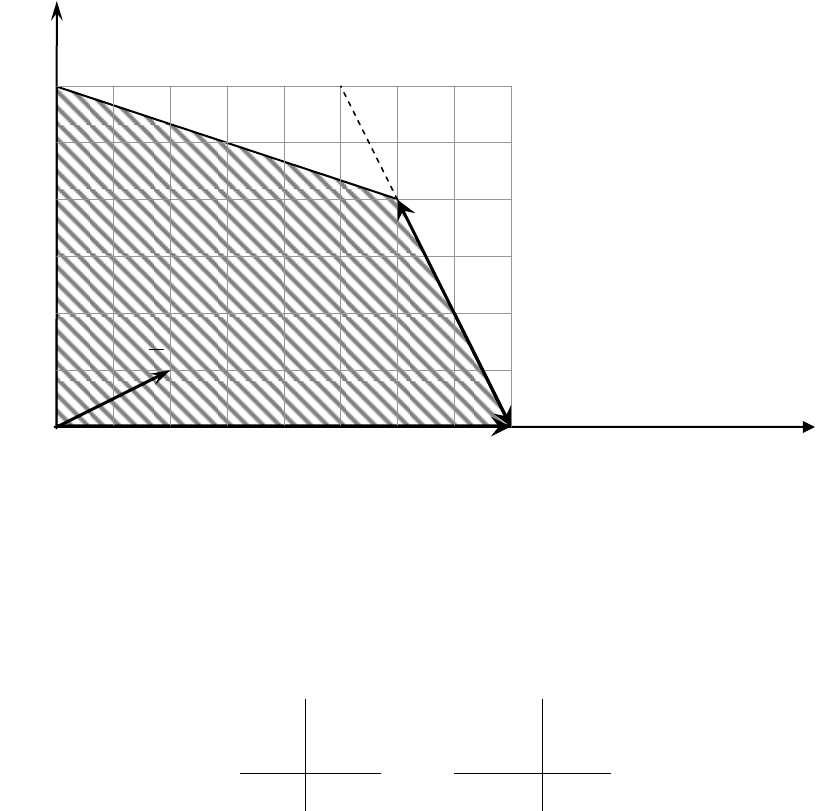
35
Базисным решением на третьем шаге будет X
3
= (6; 4; 0; 0)
(точка X
3
(6; 4) рис. 3), при котором целевая функция будет F равна
16, то есть F
3
= 16.
Общее решение запишем в виде линейной комбинации оптималь-
ных базисных решений
*
2
X
и
*
3
X
.
)0;0;4;6()1()0;10;0;8()1(*
*
3
*
2
XXX
)0;10;44;26()0;0;44;66()0;10;0;8(
.
16;10),0;10;44;26(*
max
FX
.
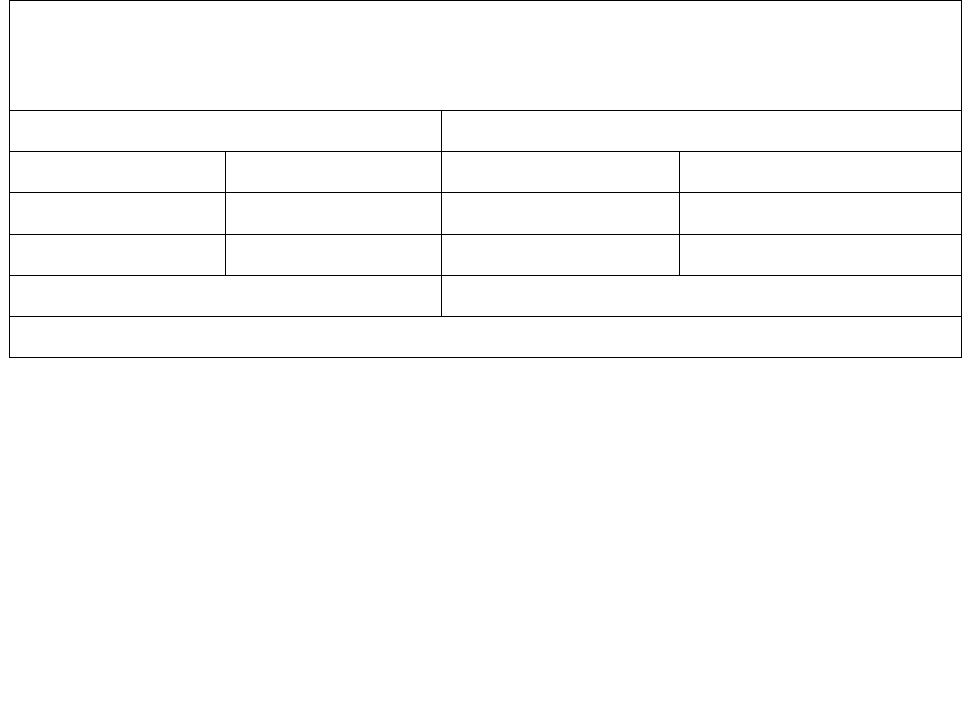
Проиллюстрируем графически процесс решения (рис. 3). Подроб-
но этот метод был описан в упражнении 1.
Рис. 3
Составим двойственную задачу. Преобразовывать систему нера-
венств не надо, так как цель задачи – максимизация, а все знаки в
системе «
».
Составим расширенную матрицу системы и транспонируем ее
)(1618
113
221
~
)(12
1612
1831
YZXF
T
.
Таким образом, получили двойственную задачу
.0,0
,13
,22
min,1618
21
21
21
21
yy
yy
yy
yyZ
X
3
X
2
n
0 1 2 3 4 5 6 7 8 x
1
x
2
6
5
4
3
2
1
X
1
36
Установим соответствие между переменными и найдем решение
двойственной задачи (табл. 32).
Таблица 32
Абсолютные значения коэффициентов
при переменных целевой функции исходной задачи,
выраженной через свободные переменные еѐ оптимального решения
основные переменные
дополнительные переменные
x
1
x
2
x
3
x
4
0
0
0
1
y
3
y
4
y
1
y
2
дополнительные переменные
основные переменные
компоненты оптимального решения двойственной задачи
Y* = (0; 1; 0; 0); Z* = F* = 16.
Контроль: Z* = 18 · 0 + 16·1 = 16.
Ответ:
16;10),0;10;44;26(*
max
FX
.
Y* = (0; 1; 0; 0); Z
min
= 16.
Задача 3. Найдите решение задачи симплексным методом, про-
иллюстрировав его графически. Составьте двойственную задачу и на
основании теорем двойственности сделайте вывод о ее решении.
3.1.
12
12
12
12
3 2 max;
4 16,
3 2 18;
0, 0.
F x x
xx
xx
xx
3.2.
12
12
12
12
2 max;
2 10,
3 15;
0, 0.
F x x
xx
xx
xx
3.3.
12
12
12
12
5 max;
5 20,
8;
0, 0.
F x x
xx
xx
xx
3.4.
12
12
12
12
3 max;
3 5 30,
3 18;
0, 0.
F x x
xx
xx
xx
3.5.
12
12
12
12
3 2 max;
2 12,
3 2 24;
0, 0.
F x x
xx
xx
xx
3.6.
12
12
12
12
6 max;
6 24,
3 21;
0, 0.
F x x
xx
xx
xx
37
3.7.
12
12
12
12
2 7 max;
2 7 35,
3 2 27;
0, 0.
F x x
xx
xx
xx
3.8.
12
12
12
12
3 max;
3 7 42,
3 24;
0, 0.
F x x
xx
xx
xx
3.9.
12
12
12
12
4 max;
4 20,
2 12;
0, 0.
F x x
xx
xx
xx
3.10.
12
12
12
12
4 3 max;
2 12,
4 3 28;
0, 0.
F x x
xx
xx
xx
3.11.
12
12
12
12
2 5 max;
2 5 30,
4 3 32;
0, 0.
F x x
xx
xx
xx
3.12.
12
12
12
12
2 max;
3 5 35,
2 14;
0, 0.
F x x
xx
xx
xx
3.13.
12
12
12
12
3 4 max;
3 4 32,
5 2 30;
0, 0.
F x x
xx
xx
xx
3.14.
12
12
12
12
5 3 max;
4 24,
5 3 35;
0, 0.
F x x
xx
xx
xx
3.15.
12
12
12
12
5 max;
3 5 40,
5 30;
0, 0.
F x x
xx
xx
xx
3.16.
12
12
12
12
5 max;
5 30,
5 2 35;
0, 0.
F x x
xx
xx
xx
3.17.
12
12
12
12
3 max;
3 21,
5 35;
0, 0.
F x x
xx
xx
xx
3.18.
12
12
12
12
5 2 max;
2 16,
5 2 40;
0, 0.
F x x
xx
xx
xx
38
3.19.
12
12
12
12
4 7 max;
4 7 63,
5 40;
0, 0.
F x x
xx
xx
xx
3.20.
12
12
12
12
5 3 max;
2 7 49,
5 3 50;
0, 0.
F x x
xx
xx
xx
3.21.
12
12
12
12
2 max;
2 16,
3 18;
0, 0.
F x x
xx
xx
xx
3.22.
12
12
12
12
2 max;
3 4 36,
2 14;
0, 0.
F x x
xx
xx
xx
3.23.
12
12
12
12
3 2 max;
5 35,
3 2 27;
0, 0.
F x x
xx
xx
xx
3.24.
12
12
12
12
3 5 max;
3 5 45,
3 21;
0, 0.
F x x
xx
xx
xx
3.25.
12
12
12
12
4 3 max;
2 7 42,
4 3 40;
0, 0.
F x x
xx
xx
xx
3.26.
12
12
12
12
3 7 max;
3 7 49,
2 18;
0, 0.
F x x
xx
xx
xx
3.27.
12
12
12
12
6 5 max;
2 7 56,
6 5 72;
0, 0.
F x x
xx
xx
xx
3.28.
12
12
12
12
7 max;
7 49,
2 20;
0, 0.
F x x
xx
xx
xx
3.29.
12
12
12
12
3 2 max;
6 42,
3 2 30;
0, 0.
F x x
xx
xx
xx
3.30.
12
12
12
12
3 max;
3 24,
12;
0, 0.
F x x
xx
xx
xx
3.31.
12
12
12
12
2 max;
3 18,
2 16;
0, 0.
F x x
xx
xx
xx
39
Упражнение 4. Найдите решение задачи симплексным методом,
проиллюстрировав его графически. Составьте двойственную задачу
и, на основании теорем двойственности, сделайте вывод
о ее решении.
.0,0
,1234
,22
max,32
21
21
21
21
xx
xx
xx
xxF
Решение.
Решим задачу симплекс-методом (подробно этот метод был опи-
сан в упражнении 2). Для этого приведем задачу к каноническому
виду
.0,0,0,0
,1234
,22
max,32
4321
421
321
21
xxxx
xxx
xxx
xxF
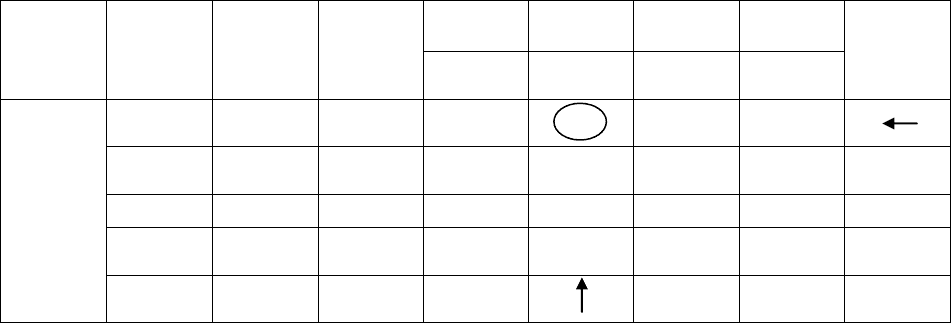
Внесѐм данные задачи в симплекс-таблицу 33.
Таблица 33
План
Базис
С
б
b
i
2
3
0
0
d
i
x
1
x
2
x
3
x
4
I
x
3
0
2
–2
1
1
0
2
x
4
0
12
4
–3
0
1
F
=
0
–2
–3
0
0
Базисным решением на первом шаге будет X
1
= (0; 0; 2; 12) (точка
X
1
(0; 0) рис. 4), при котором целевая функция будет F равна 0, то есть
F
1
= 0.
Для базисного решения X
1
критерий оптимальности не выполнен,
так как в столбцах, соответствующих свободным переменным x
1
и x
2
,
в целевой функции есть отрицательные элементы (–2 и –3); выбираем
из них наименьший.
Чтобы перейти к построению плана II, нужно перевести перемен-
ную x
2
в базис. Тогда столбец x
2
– разрешающий столбец. Заполняем
