Кирсанова О.В., Семёнова Г.А. Математическое программирование (типовой расчёт)
Подождите немного. Документ загружается.

120
б)
1334
,2/173/13/35
t
tt
–28/5 < t 13, тогда в свободные пере-
водим переменную x
4
(план II).
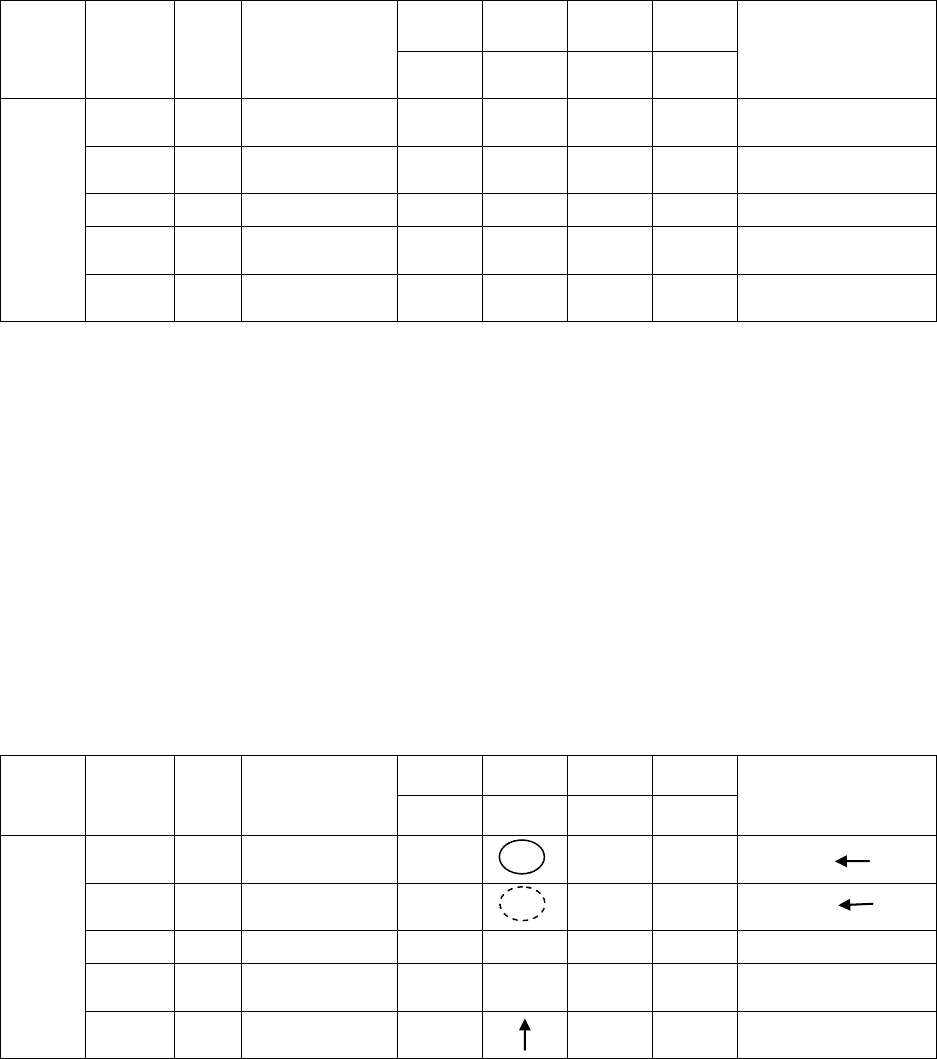
Вычисляем элементы новой симплекс-таблицы 87 в случае а).
Таблица 87
План
Базис
С
б
b
i
3
2
0
0
d
i
x
1
x
2
x
3
x
4
II
x
1
3
35/3 + 1/3t
1
5/3
1/3
0
x
4
0
–28/3 – 5/3t
0
–7/3
–2/3
1
F
=
35 + t
0
3
1
0
Базисным решением в таком случае будет
X
2
= (35/3 + 1/3t; 0; 0; –28/3 – 5/3t),
при котором целевая функция будет F равна 35 + t, то есть
F
2
= 35 + t.
Для решения X
2
выполнен критерий оптимальности, так как в це-
левой функции нет отрицательных элементов. Кроме того, все коэф-
фициенты при свободных переменных (x
2
, x
3
) отличны от нуля, сле-
довательно, полученное решение X
2
оптимально и единственно.
Вычисляем элементы новой симплекс-таблицы 88 в случае б).
Таблица 88
План
Базис
С
б
b
i
3
2
0
0
d
i
x
1
x
2
x
3
x
4
II
x
3
0
14 + 5/2t
0
7/2
1
–3/2
4+5/7t III
x
1
3
7 – 1/2t
1
1/2
0
1/2
14 – t III
F
=
21 – 3/2t
0
–1/2
0
3/2
Базисным решением в таком случае будет X
2
=
=(7–1/2t; 0; 14 + 5/2t; 0), при котором целевая функция будет F равна
21 – 3/2t, то есть F
2
= 21 – 3/2t.
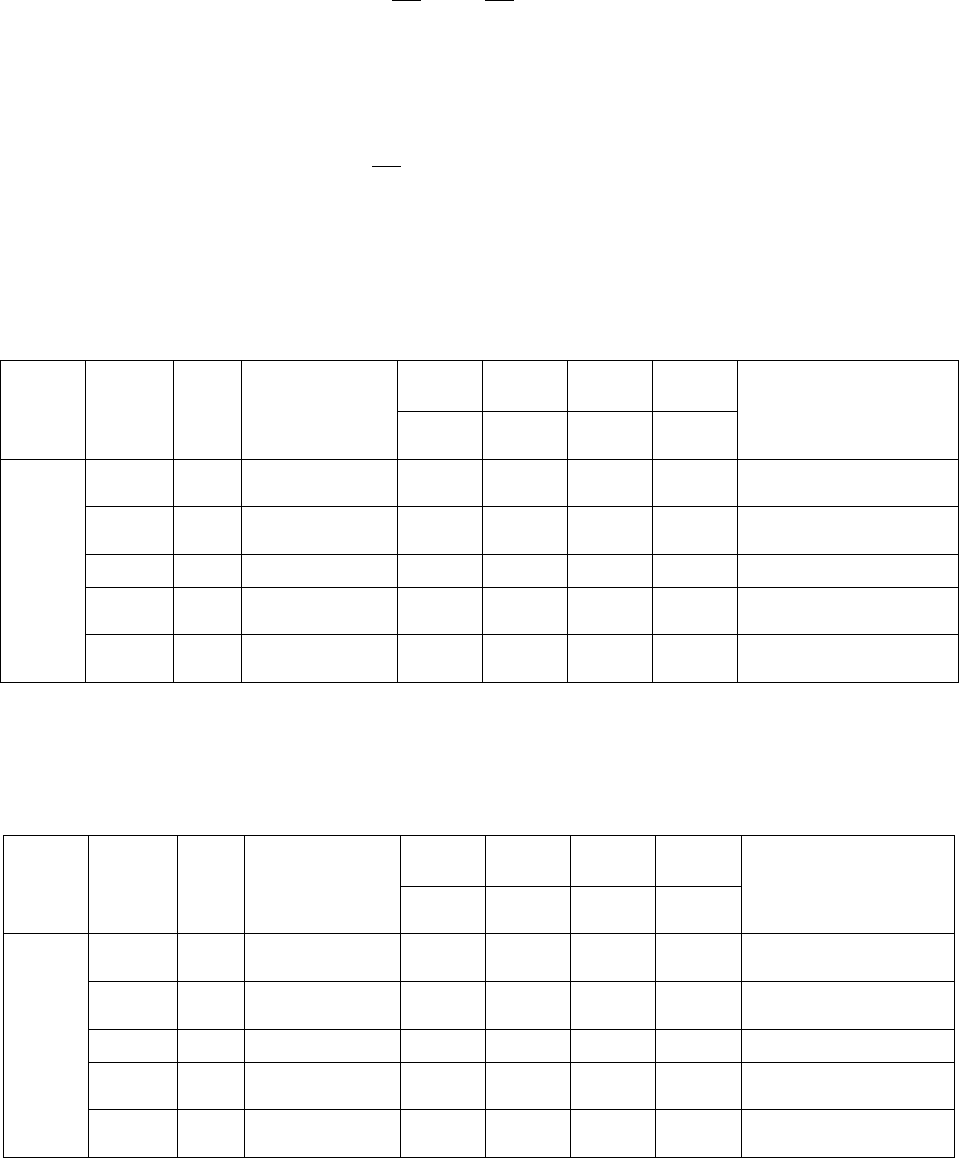
121
Для базисного решения X
2
критерий оптимальности не выпол-
нен, так как в целевой функции есть отрицательные элементы. Чтобы
перейти к построению плана III, нужно перевести переменную x
2
в
базис.
При выборе базисной переменной, которую нужно перевести в
свободные, возможны два случая:
а)
,
6
35
5
25
,13
,5/28
,147/54
t
t
t
tt
тогда в свободные переводим переменную x
3
(план III);
б)
,13
6
35
,13
,5/28
,147/54
t
t
t
tt
тогда в свободные переводим переменную x
1
(план III).
Вычисляем элементы новой симплекс-таблицы 89 в случае а).
Таблица 89
План
Базис
С
б
b
i
3
2
0
0
d
i
x
1
x
2
x
3
x
4
III
x
2
2
4 + 5/7t
0
1
2/7
–-3/7
x
1
3
5 – 6/7t
1
0
–1/7
5/7
F
=
23 – 8/7t
0
0
1/7
9/7
Базисным решением в таком случае будет X
3
=
=(5 – 6/7t; 4 + 5/7t; 0; 0), при котором целевая функция будет F равна
23 – 8/7t, то есть F
3
= 23 – 8/7t.
Таблица 90
План
Базис
С
б
b
i
3
2
0
0
d
i
x
1
x
2
x
3
x
4
III
x
3
0
–35 + 6t
–7
0
1
–5
x
2
2
14 – t
2
1
0
1
F
=
28 – 2t
1
0
0
2

122
Для решения X
3
выполнен критерий оптимальности, так как в це-
левой функции нет отрицательных элементов. Кроме того, все коэф-
фициенты при свободных переменных (x
3
, x
4
) отличны от нуля, сле-
довательно, полученное решение X
3
оптимально и единственно.
Вычисляем элементы новой симплекс-таблицы 90 в случае б).
Базисным решением в таком случае будет X
3
=
= (0; 14 – t; –35 + 6t; 0), при котором целевая функция будет F равна
28 – 2t, то есть F
3
= 28 – 2t.
Для решения X
3
выполнен критерий оптимальности, так как в
целевой функции нет отрицательных элементов. Кроме того, все ко-
эффициенты при свободных переменных (x
1
, x
4
) отличны от нуля,
следовательно, полученное решение X
3
оптимально и единственно.
Ответ:
если
5
28
;34t
, то X* = (35/3 + 1/3t; 0; 0; –28/3 – 5/3t),
F
max
= 35 + t,
если
6
35
;
5
28
t
, то X* = (5 – 6/7t; 4 + 5/7t; 0; 0), F
max
= 23 – 8/7t,
если
13;
6
35
t
, то X* = (0; 14 – t; –35 + 6t; 0), F
max
= 28 – 2t.
Задача 5. Найдите решение задачи параметрического программи-
рования симплексным методом.
5.1.
12
12
12
12
4 max;
2 7 49 ,
5 3 50 ;
0, 0;
48;49 .
F x x
x x t
x x t
xx
t
5.2.
12
12
12
12
3 max;
3 21 ,
5 35 ;
0, 0;
20;34 .
F x x
x x t
x x t
xx
t
5.3.
12
12
12
12
4 3 max;
3 4 36 ,
2 14 ;
0, 0;
35;13 .
F x x
x x t
x x t
xx
t
5.4.
12
12
12
12
4 max;
4 7 63 ,
5 40 ;
0, 0;
62;39 .
F x x
x x t
x x t
xx
t

123
5.5.
12
12
12
12
2 max;
3 5 45 ,
3 21 ;
0, 0;
44;20 .
F x x
x x t
x x t
xx
t
5.6.
12
12
12
12
2 3 max;
2 16 ,
3 18 ;
0, 0;
15;17 .
F x x
x x t
x x t
xx
t
5.7.
12
12
12
12
3 5 max;
3 7 49 ,
2 18 ;
0, 0;
48;19 .
F x x
x x t
x x t
xx
t
5.8.
12
12
12
12
2 5 max;
5 35 ,
3 2 27 ;
0, 0;
34;26 .
F x x
x x t
x x t
xx
t
5.9.
12
12
12
12
2 3 max;
2 7 42 ,
4 3 40 ;
0, 0;
41;39 .
F x x
x x t
x x t
xx
t
5.10.
12
12
12
12
5 max;
2 16 ,
5 2 40 ;
0, 0;
15;39 .
F x x
x x t
x x t
xx
t
5.11.
12
12
12
12
2 3 max;
2 7 56 ,
6 5 72 ;
0, 0;
55;71 .
F x x
x x t
x x t
xx
t
5.12.
12
12
12
12
3 3 max;
2 12 ,
3 2 24 ;
0, 0;
11;23 .
F x x
x x t
x x t
xx
t
5.13.
12
12
12
12
3 max;
7 49 ,
2 20 ;
0, 0;
48;19 .
F x x
x x t
x x t
xx
t
5.14.
12
12
12
12
2 3 max;
2 7 35 ,
3 2 27 ;
0, 0;
34;26 .
F x x
x x t
x x t
xx
t
5.15.
12
12
12
12
2 3 max;
3 24 ,
12 ;
0, 0;
23;11 .
F x x
x x t
x x t
xx
t
5.16.
12
12
12
12
4 max;
6 42 ,
3 2 30 ;
0, 0;
41;29 .
F x x
x x t
x x t
xx
t

124
5.17.
12
12
12
12
4 3 max;
4 16 ,
3 2 18 ;
0, 0;
15;17 .
F x x
x x t
x x t
xx
t
5.18.
12
12
12
12
2 5 max;
3 18 ,
2 16 ;
0, 0;
17;15 .
F x x
x x t
x x t
xx
t
5.19.
12
12
12
12
2 5 max;
5 20 ,
8;
0, 0;
19;7 .
F x x
x x t
x x t
xx
t
5.20.
12
12
12
12
3 2 max;
2 10 ,
3 15 ;
0, 0;
9;14 .
F x x
x x t
x x t
xx
t
5.21.
12
12
12
12
3 2 max;
3 5 30 ,
3 18 ;
0, 0;
29;17 .
F x x
x x t
x x t
xx
t
5.22.
12
12
12
12
4 3 max;
4 24 ,
5 3 35 ;
0, 0;
23;34 .
F x x
x x t
x x t
xx
t
5.23.
12
12
12
12
3 max;
6 24 ,
3 21 ;
0, 0;
23;14 .
F x x
x x t
x x t
xx
t
5.24.
12
12
12
12
3 4 max;
2 5 30 ,
4 3 32 ;
0, 0;
29;31 .
F x x
x x t
x x t
xx
t
5.25.
12
12
12
12
4 3 max;
3 7 42 ,
3 24 ;
0, 0;
41;23 .
F x x
x x t
x x t
xx
t
5.26.
12
12
12
12
2 max;
3 4 32 ,
5 2 30 ;
0, 0;
31;29 .
F x x
x x t
x x t
xx
t
5.27.
12
12
12
12
2 max;
4 20 ,
2 12 ;
0, 0;
19;11 .
F x x
x x t
x x t
xx
t
5.28.
12
12
12
12
4 max;
3 5 40 ,
5 30 ;
0, 0;
39;29 .
F x x
x x t
x x t
xx
t

125
5.29.
12
12
12
12
3 4 max;
2 12 ,
4 3 28 ;
0, 0;
11;27 .
F x x
x x t
x x t
xx
t
5.30.
12
12
12
12
2 5 max;
5 30 ,
5 2 35 ;
0, 0;
29;34 .
F x x
x x t
x x t
xx
t
5.31.
12
12
12
12
3 2 max;
3 5 35 ,
2 14 ;
0, 0;
34;13 .
F x x
x x t
x x t
xx
t
3.3. Нелинейное прогаммирование
Упражнение 6. Используя графический метод, найдите решение
задачи нелинейного программирования.
.0,0
,5
,4
extr,
21
21
21
2
2
2
1
xx
xx
xx
xxF
Решение.
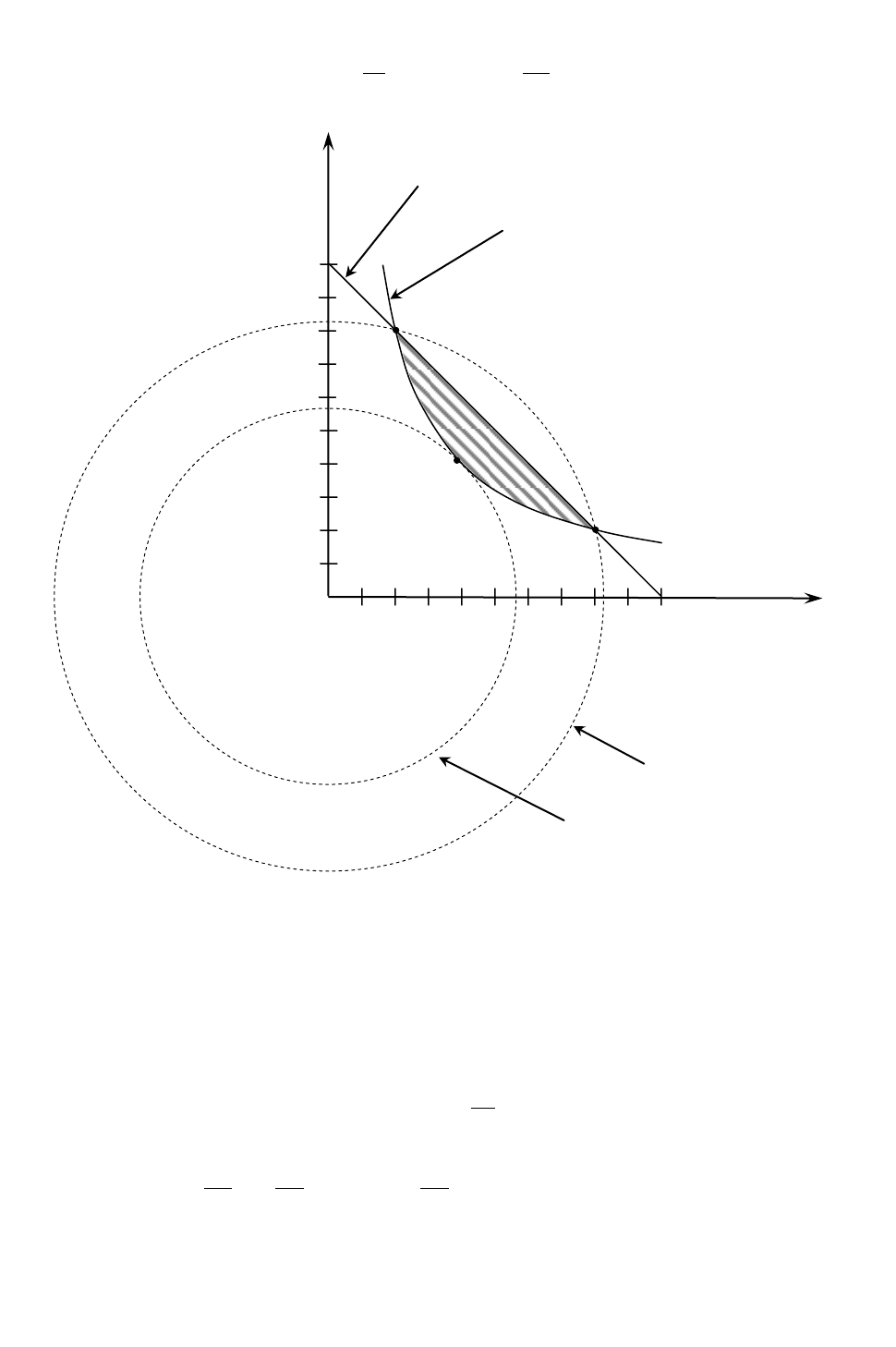
Построим область допустимых решений задачи нелинейного про-
граммирования (рис. 16).
Для нахождения решения нужно определить такие точки области,
в которых функция
2
2
2
1
xxF
принимает максимальное и минималь-
ное значения.
Построим линию уровня
hxx
2
2
2
1
, где h – некоторая постоян-
ная величина, и исследуем еѐ поведение при различных значениях h.
При каждом значении h получаем окружность с центром в начале ко-
ординат и радиусом h. Эта окружность тем больше удалена от начала
координат, чем больше значение h.
Проводя из начала координат окружности разных радиусов, по-
лучаем, что минимальное значение функция F принимает в точке A, в
которой окружность касается области решений. Для определения ко-
ординат точки A воспользуемся равенством угловых коэффициентов
касательной к окружности
hxx
2
2
2
1
и касательной к гиперболе
4
21
xx
.
Рассматривая переменную x
2
как неявную функцию переменной
x
1
, почленно дифференцируем уравнение окружности
hxx
2
2
2
1
и по-
лучим:
1 2 2
2 2 0x x x
1
2
2
x
x
x
.
126
Аналогично, дифференцируя уравнение гиперболы
4
21
xx
, по-
лучим:
2
1
4
x
x
2
2
1
4
x
x
.
Рис. 16
Угловой коэффициент касательной равен значению производной
в данной точке. Поэтому, чтобы найти координаты точки A, лежащей
на гиперболе
4
21
xx
, достаточно приравнять производные и решить
систему уравнений:
.2
,2
,0,0
,4
4
,
4
,0,0
,
4
,4
2
1
21
4
1
1
2
21
2
1
2
1
21
x
x
xx
x
x
x
xx
x
x
x
xx
В результате
*
min
X
= A(2: 2) и
*
min
F
= 8.
0
1
1
2
2
3
x
1
x
2
5
5
4
4
3
5
21
xx
4
21
xx
1
2
2
2
1
hxx
2
2
2
2
1
hxx
A
B
C

127
Из рис. 16 видно, что целевая функция принимает максимальное
значение в точках B и C. Координаты точек B и C можно найти из
системы уравнений:
.1
,4
,4
,1
,0,0
,5
,4
2
1
2
1
21
21
21
x
x
x
x
xx
xx
xx
Решая эту систему, получим
*
1max,
X
= B(1; 4),
*
2max,
X
= C(4; 1) и
*
max
F
= 17.
Ответ:
*
min
X
= (2: 2) и
*
min
F
= 8,
*
1max,
X
= (1; 4),
*
2max,
X
= (4; 1) и
*
max
F
= 17.
Задача 6. Используя графический метод, найдите решение задачи
нелинейного программирования.
6..1
12
22
12
12
2 3 ;
16;
0, 0.
F x x extr
xx
xx
6.2.
22
12
12
12
12
5 4 ;
5 4 20,
3 2 30;
0, 0.
F x x extr
xx
xx
xx
6.3.
22
12
12
1
2
12
1 1 ;
4,
6,
5;
0, 0.
F x x extr
xx
x
x
xx
6.4.
12
12
1
2
12
2 3 ;
3,
4,
5;
0, 0.
F x x extr
xx
x
x
xx
6.5.
22
12
12
12
12
6 2 ;
2 5 20,
2 10;
0, 0.
F x x extr
xx
xx
xx
6.6.
22
12
12
1
2
12
1 2 ;
16,
3,5,
3,5;
0, 0.
F x x extr
xx
x
x
xx

128
6.7.
12
22
12
12
2;
36;
0, 0.
F x x extr
xx
xx
6.8.
22
12
12
12
12
1 1 ;
5 4 20,
3 2 30;
0, 0.
F x x extr
xx
xx
xx
6.9.
22
12
12
1
2
12
2 1 ;
5,
5,
6;
0, 0.
F x x extr
xx
x
x
xx
6.10.
12
12
1
2
12
3 2 ;
2,
6,
7;
0, 0.
F x x extr
xx
x
x
xx
6.11.
22
12
12
12
12
2 1 ;
2 5 20,
2 10;
0, 0.
F x x extr
xx
xx
xx
6.12.
22
12
12
1
2
12
1 1 ;
25,
4,5,
4,5;
0, 0.
F x x extr
xx
x
x
xx
6.13.
12
22
12
12
2;
25;
0, 0.
F x x extr
xx
xx
6.14.
22
12
12
12
12
3 4 ;
3 8 24,
4 7 28;
0, 0.
F x x extr
xx
xx
xx
6.15.
22
12
12
1
2
12
1 2 ;
6,
4,
5;
0, 0.
F x x extr
xx
x
x
xx
6.16.
12
12
1
2
12
2;
5,
5,
4;
0, 0.
F x x extr
xx
x
x
xx
6.17.
22
12
12
12
12
1 1 ;
3 5 15,
5 3 15;
0, 0.
F x x extr
xx
xx
xx
6.18.
22
12
12
1
2
12
1 1 ;
36,
5,5,
5,5;
0, 0.
F x x extr
xx
x
x
xx

129
6.19.
12
22
12
12
2;
4;
0, 0.
F x x extr
xx
xx
6.20.
22
12
12
12
12
3 1 ;
3 8 24,
4 7 28;
0, 0.
F x x extr
xx
xx
xx
6.21.
22
12
12
1
2
12
1 1 ;
3,
5,
4;
0, 0.
F x x extr
xx
x
x
xx
6.22.
12
12
1
2
12
2;
4,
7,
5;
0, 0.
F x x extr
xx
x
x
xx
6.23.
22
12
12
12
12
2 6 ;
3 5 15,
5 3 15;
0, 0.
F x x extr
xx
xx
xx
6.24.
2
2
12
12
1
2
12
2;
4,
6,5,
6,5;
0, 0.
F x x extr
xx
x
x
xx
6.25.
12
22
12
12
3;
9;
0, 0.
F x x extr
xx
xx
6.26.
22
12
12
12
12
2 2 ;
6 7 42,
3 2 6;
0, 0.
F x x extr
xx
xx
xx
6.27.
22
12
12
1
2
12
2 2 ;
2,
3,
6;
0, 0.
F x x extr
xx
x
x
xx
6.28.
12
12
1
2
12
2;
2,
8,
6;
0, 0.
F x x extr
xx
x
x
xx
6.29.
22
12
12
12
12
1 1 ;
6 7 42,
3 2 6;
0, 0.
F x x extr
xx
xx
xx
6.30.
2
2
12
12
1
2
12
2;
9,
2,8,
2,8;
0, 0.
F x x extr
xx
x
x
xx
