Кирсанова О.В., Семёнова Г.А. Математическое программирование (типовой расчёт)
Подождите немного. Документ загружается.


100
1.5.
12
12
12
12
12
3 4 max;
2 16,
5 3 50;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.6.
12
12
12
12
12
3 2 max;
3 7 49,
2 20;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.7.
12
12
12
12
12
3 4 max;
7 49,
2 18;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.8.
12
12
12
12
12
3 2 max;
3 5 45,
2 14;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.9.
12
12
12
12
12
4 3 max;
3 18,
3 2 30;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.10.
12
12
12
12
12
2 3 max;
2 16,
2 16;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.11.
12
12
12
12
12
4 3 max;
3 2 8,
4 10;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.12.
12
12
12
12
12
8 5 max;
5 2 20,
6;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.13.
12
12
12
12
12
2 max;
4 3 24,
3;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.14.
12
12
12
12
12
2 max;
6 4 24,
3 3 9;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.15.
12
12
12
12
12
3 2 max;
13,
6;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.16.
12
12
12
12
12
3 max;
5 35,
3 18;
0, 0;
, Z.
F x x
xx
xx
xx
xx

101
1.17.
12
12
12
12
12
2 max;
5 30,
3 5 35;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.18.
12
12
12
12
12
3 5 max;
2 12,
2 14;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.19.
12
12
12
12
12
3 2 max;
4 16,
8;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.20.
12
12
12
12
12
4 3 max;
2 16,
3 5 50;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.21.
12
12
12
12
12
4 3 max;
7 49,
2 18;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.22.
12
12
12
12
12
2 3 max;
7 3 49,
2 20;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.23.
12
12
12
12
12
2 3 max;
5 3 45,
2 14;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.24.
12
12
12
12
12
3 4 max;
3 18,
2 3 30;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.25.
12
12
12
12
12
3 2 max;
2 16,
2 16;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.26.
12
12
12
12
12
3 4 max;
2 3 8,
4 10;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.27.
12
12
12
12
12
5 8 max;
2 5 20,
6;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.28.
12
12
12
12
12
2 max;
3 4 24,
3;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.29.
12
12
12
12
12
2 max;
4 6 24,
3;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.30.
12
12
12
12
12
2 3 max;
13,
6;
0, 0;
, Z.
F x x
xx
xx
xx
xx
1.31.
12
12
12
12
12
4 3 max;
2 16,
3 2 27;
0, 0;
, Z.
F x x
xx
xx
xx
xx
102
Упражнение 2. Найдите решение задачи
.,
,0,0
,213
,3643
max,34
21
21
21
21
21
Z
xx
xx
xx
xx
xxF
методами: а) графическим; б) ветвей и границ графически.
Решение.
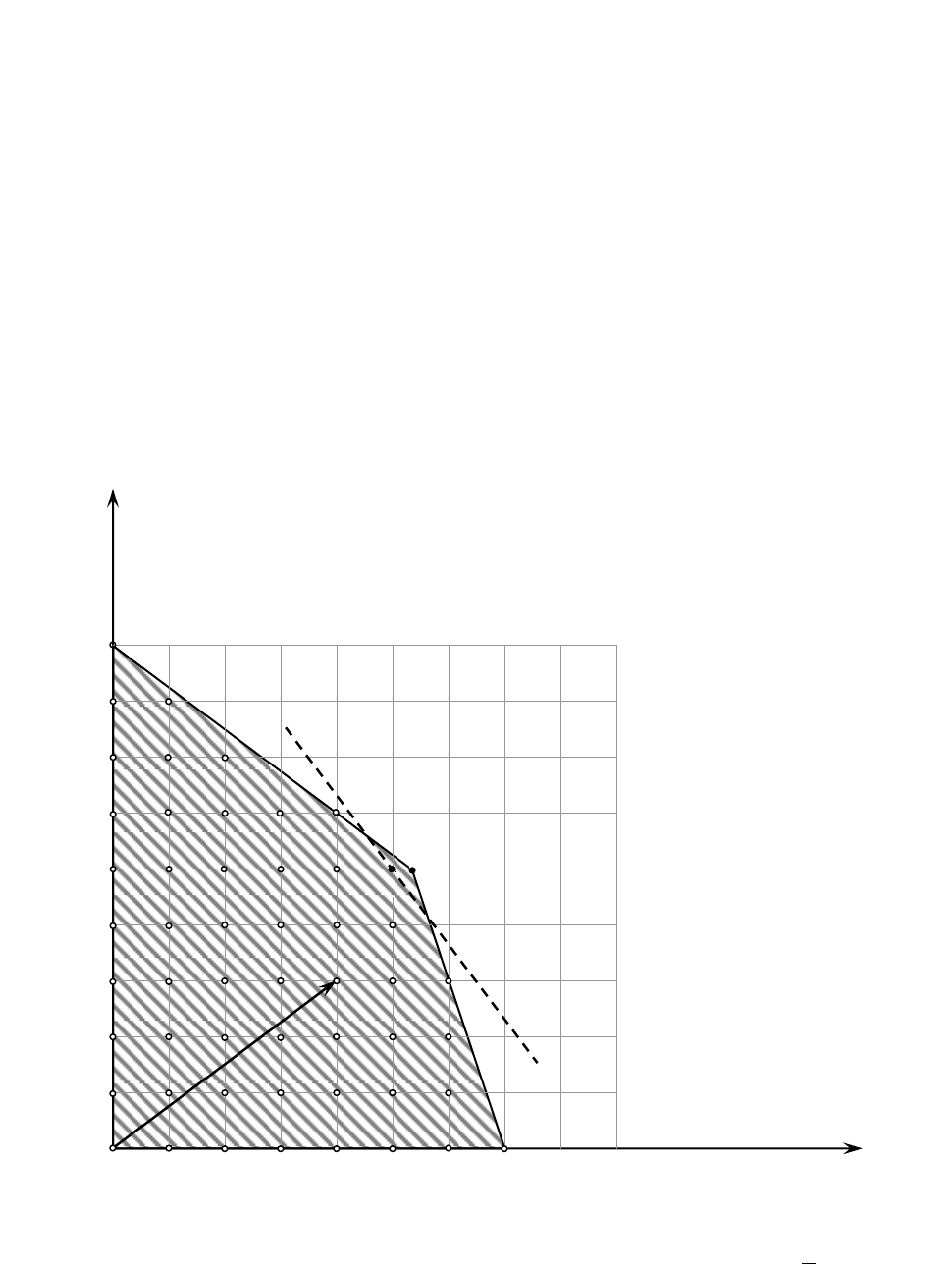
а) графический метод. Область допустимых значений непрерыв-
ной задачи представлена на рис. 11, а множество допустимых реше-
ний задачи целочисленного линейного программирования – точками
на этом рисунке.
Рис. 11
Перемещаем линию уровня по направлению вектора
n
(подроб-
нее смотри упражнение 1, глава 1). Точкой выхода из области допус-
тимых решений непрерывной задачи является точка B(16/3; 5), а для
целочисленной задачи –
*
Z
X
(5; 5).
Таким образом,
35),5;5(
**
ZZ
FX
;
x
2
9
8
7
6
5
4
3
2
1
B
n
0 1 2 3 4 5 6 7 8 9 x
1
X
Z
*
103
б) Метод ветвей и границ.
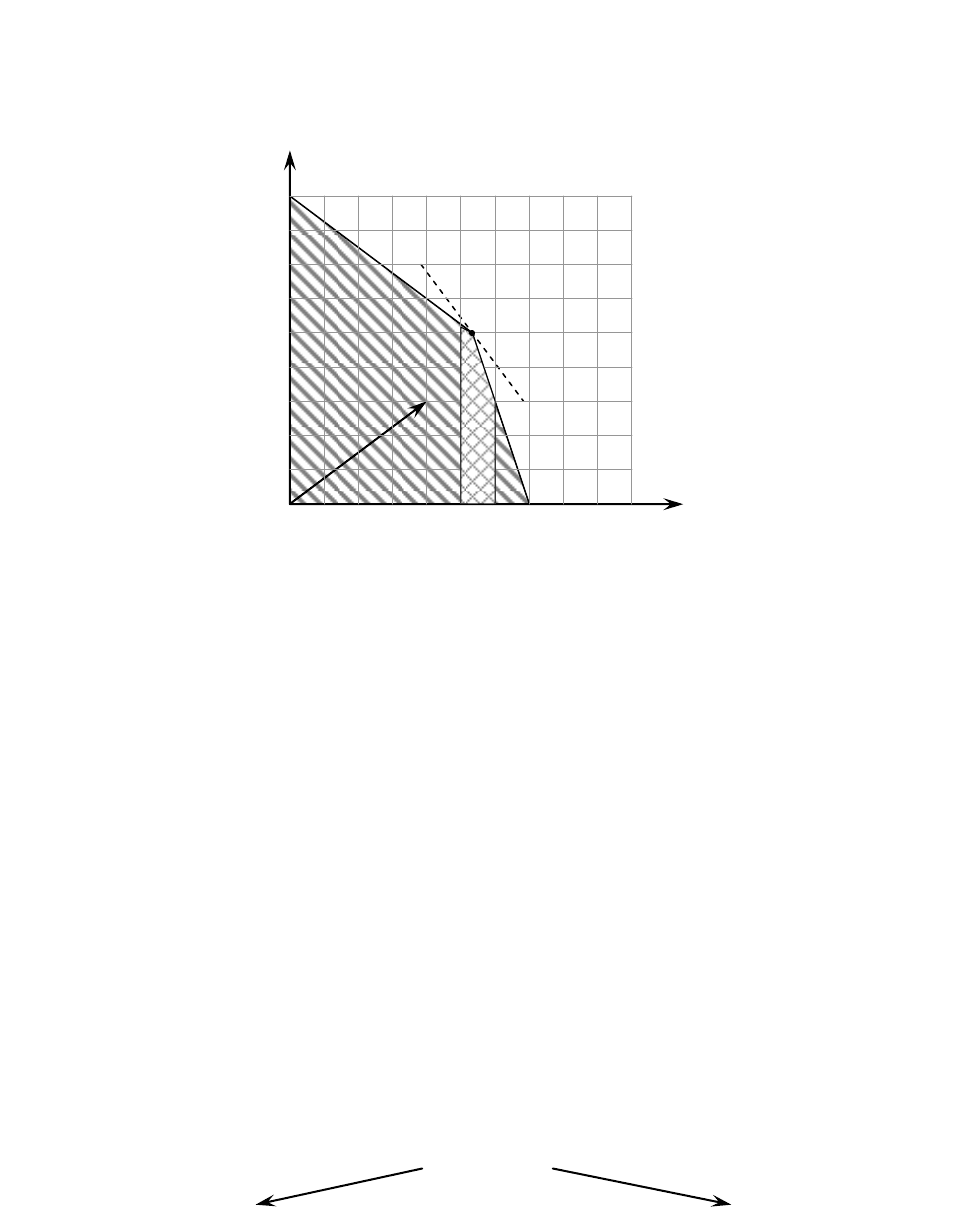
Начальная задача линейного программирования (задача 1) полу-
чается путѐм отбрасывания условия целочисленности. Еѐ оптималь-
ным решением будет точка X
1
(16/3; 5), в которой F
1
= 109/3 (рис. 12).
Рис. 12
Это решение не удовлетворяет условию целочисленности. Метод
ветвей и границ изменяет пространство решений задачи линейного
программирования так, что в конечном счѐте получается оптималь-
ное решение задачи целочисленного линейного программирования.
Для этого сначала выбирается одна из целочисленных перемен-
ных, значение которой в оптимальном решении задачи 1 не является
целочисленным. Выбирая x
1
, замечаем, что область 5 < x
1
< 6 про-
странства допустимых решений задачи 1 не содержит целочисленных
значений переменной x
1
, и, следовательно, может быть исключена из
рассмотрения как бесперспективная. Это эквивалентно замене исход-
ной задачи 1 двумя новыми задачами линейного программирования
(задача 2 и задача 3).
задача 1
задача 2
задача 3
.5
,213
,3643
1
21
21
x
xx
xx
.6
,213
,3643
1
21
21
x
xx
xx
x
2
9
8
7
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8 9 x
1
X
1
n
104
Отметим, что среди вспомогательных задач могут оказаться та-
кие, что область допустимых решений состоит из единственной точ-
ки, которая и является оптимальным решеием, и такие, которые не
имеют решения.
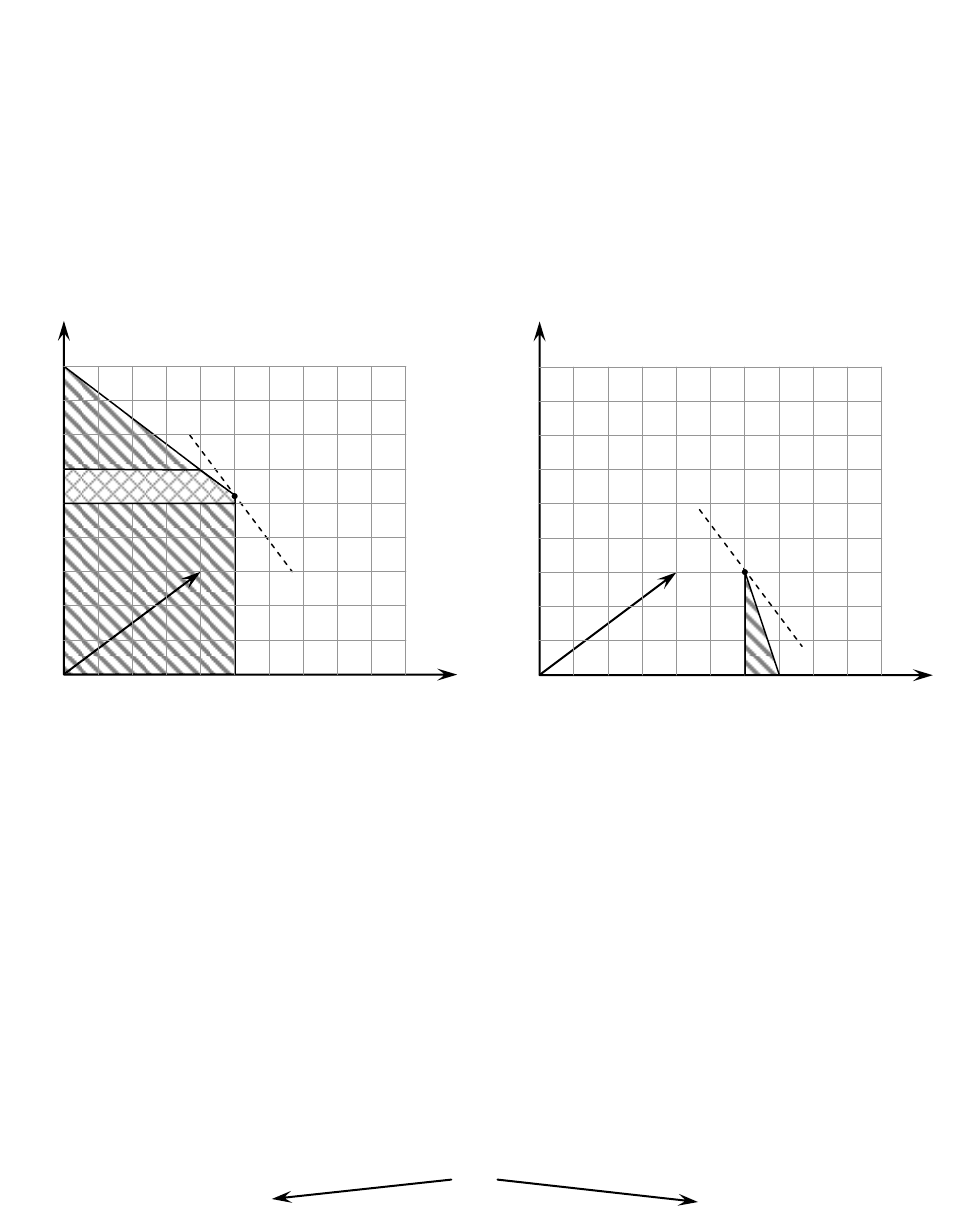
На рис. 13 а и 13 б изображены пространства допустимых реше-
ний задач 2 и 3. Оптимальное решение исходной задачи находится в
пространстве допустимых решений либо задачи 2, либо задачи 3, сле-
довательно, обе задачи должны быть решены.
Рис. 13 а
Рис. 13 б
X
2
(5; 21/4) и F
2
= 143/4;
X
3
(6; 3) и F
3
= 33.
Оптимальное решение задачи 2 не является целочисленным, по-
этому обращаемся к целочисленной переменной x
2
, значение которой
в оптимальном решении задачи 2 не является целочисленным. Так
как в области 5 < x
2
< 6 пространства допустимых решений задачи 1
не содержится целочисленных значений переменной x
2
, заменяем за-
дачу 2 двумя новыми задачами линейного программирования (задача
4 и задача 5), которые обе должны быть решены.
задача 2
задача 4
задача 5
.5
,5
,213
,3643
2
1
21
21
x
x
xx
xx
.6
,5
,213
,3643
2
1
21
21
x
x
xx
xx
x
2
9
8
7
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8 9 x
1
X
2
n
x
2
9
8
7
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8 9 x
1
X
3
n
105
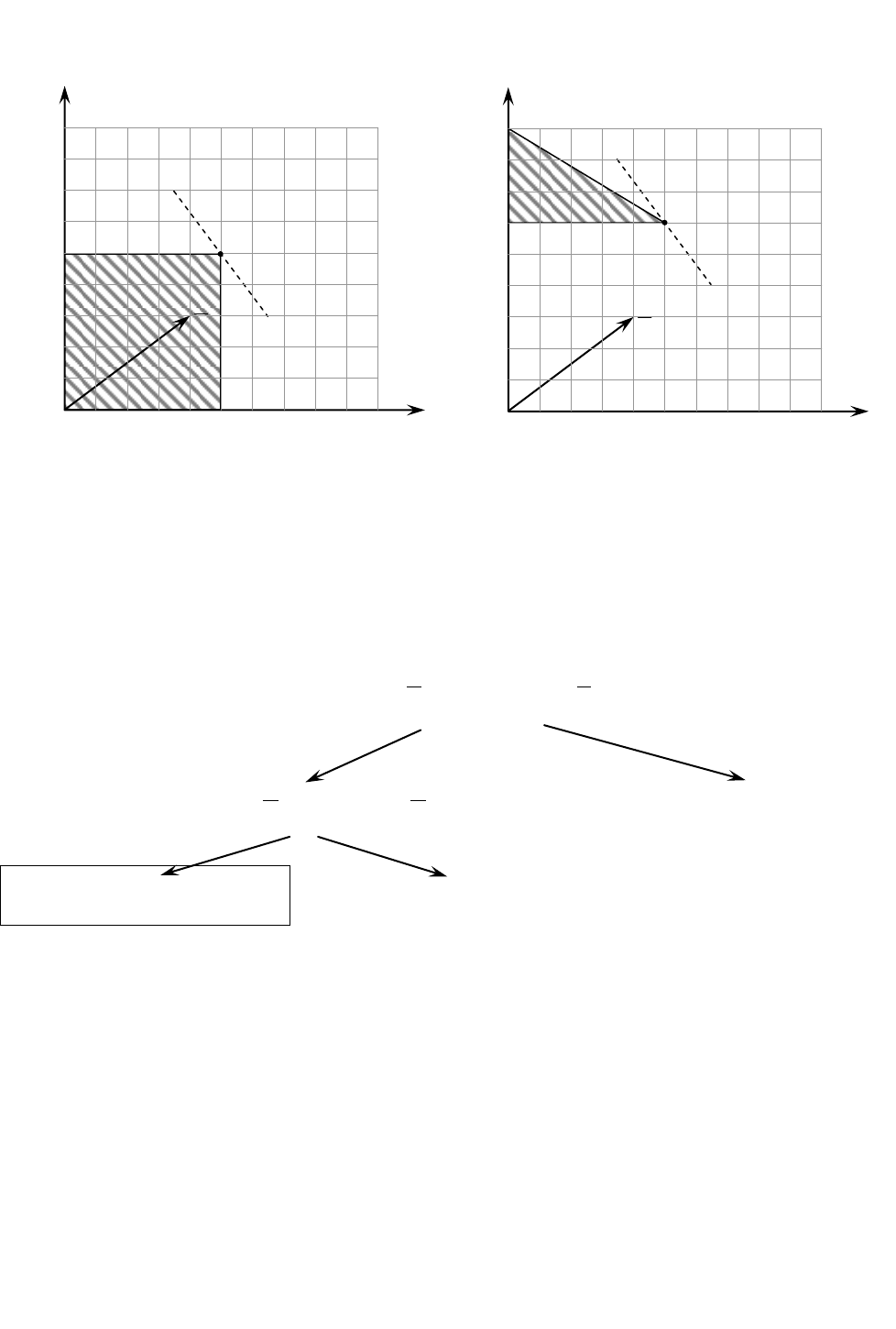
На рис. 14 а и 14 б изображены пространства допустимых реше-
ний задач 4 и 5.
Рис. 14 а
Рис. 14 б
X
4
(5; 5) и F
4
= 5;
X
5
(4; 6) и F
5
= 34.
Оптимальные решения задач 4 и 5 – целочисленные, поэтому
дальнейшего ветвления не требуется.
Таким образом, схематически:
1.
.
3
1
36,5;
3
1
5
11
FX
2.
.
4
3
35,
4
1
5;5
22
FX
3.
.33,3;6
33
FX
4.
.35,5;5
44
FX
3.
.34,6;4
35
FX
Ответ:
.35,5;5*
max
FX
Задача 2. Найдите решение задачи методами:
а) графическим;
б) ветвей и границ графически.
2.1.
12
12
12
12
12
3 4 max;
6 42,
2 16;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.2.
12
12
12
12
12
4 3 max;
3 18,
3 2 30;
0, 0;
, Z.
F x x
xx
xx
xx
xx
x
2
9
8
7
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8 9 x
1
X
4
n
x
2
9
8
7
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8 9 x
1
X
5
n

106
2.3.
12
12
12
12
12
2 5 max;
3 24,
5 2 35;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.4.
12
12
12
12
12
3 2 max;
3 5 45,
2 14;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.5.
12
12
12
12
12
4 5 max;
2 7 42,
6 5 72;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.6.
12
12
12
12
12
3 4 max;
2 7 56,
4 3 40;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.7.
12
12
12
12
12
3 2 max;
3 7 49,
2 20;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.8.
12
12
12
12
12
3 4 max;
7 49,
2 18;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.9.
12
12
12
12
12
3 max;
3 21,
5 40;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.10.
12
12
12
12
12
5 2 max;
4 7 63,
5 35;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.11.
12
12
12
12
12
3 4 max;
2 16,
5 3 50;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.12.
12
12
12
12
12
3 3 max;
2 7 49,
5 2 40;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.13.
12
12
12
12
12
2 3 max;
4 16,
8;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.14.
12
12
12
12
12
2 max;
3 2 18,
5 20;
0, 0;
, Z.
F x x
xx
xx
xx
xx

107
2.15.
.,
,0,0
,183
,102
max,23
21
21
21
21
21
Z
xx
xx
xx
xx
xxF
2.16.
12
12
12
12
12
3 4 max;
3 5 30,
3 15;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.17.
12
12
12
12
12
2 3 max;
2 12,
3 2 27;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.18.
12
12
12
12
12
3 4 max;
2 7 35,
3 2 24;
0, 0;
,.
F x x
xx
xx
xx
xx
Z
2.19.
.,
,0,0
,243
,246
max,2
21
21
21
21
21
Z
xx
xx
xx
xx
xxF
2.20.
12
12
12
12
12
5 2 max;
3 7 42,
3 21;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.21.
12
12
12
12
12
2 3 max;
4 20,
4 3 32;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.22.
12
12
12
12
12
3 2 max;
2 5 30,
2 12;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.23.
12
12
12
12
12
5 3 max;
2 12,
2 14;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.24.
12
12
12
12
12
2 2 max;
3 5 35,
4 3 28;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.25.
12
12
12
12
12
2 max;
3 4 32,
5 30;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.26.
12
12
12
12
12
3 2 max;
3 5 40,
5 2 30;
0, 0;
, Z.
F x x
xx
xx
xx
xx

108
2.27.
12
12
12
12
12
2 3 max;
4 24,
5 2 35;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.28.
12
12
12
12
12
2 max;
5 30,
5 3 35;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.29.
12
12
12
12
12
4 3 max;
2 16,
3 2 27;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.30.
12
12
12
12
12
3 max;
5 35,
3 18;
0, 0;
, Z.
F x x
xx
xx
xx
xx
2.31.
12
12
12
12
12
4 3 max;
3 4 36,
3 21;
0, 0;
, Z.
F x x
xx
xx
xx
xx
3.2. Параметрическое программирование
Упражнение 3. Найдите решение задачи параметрического про-
граммирования графическим методом.
.10;0
,0,0
,122
,204
max,)13()3(
21
21
21
21
t
xx
xx
xx
xtxtF
Решение.
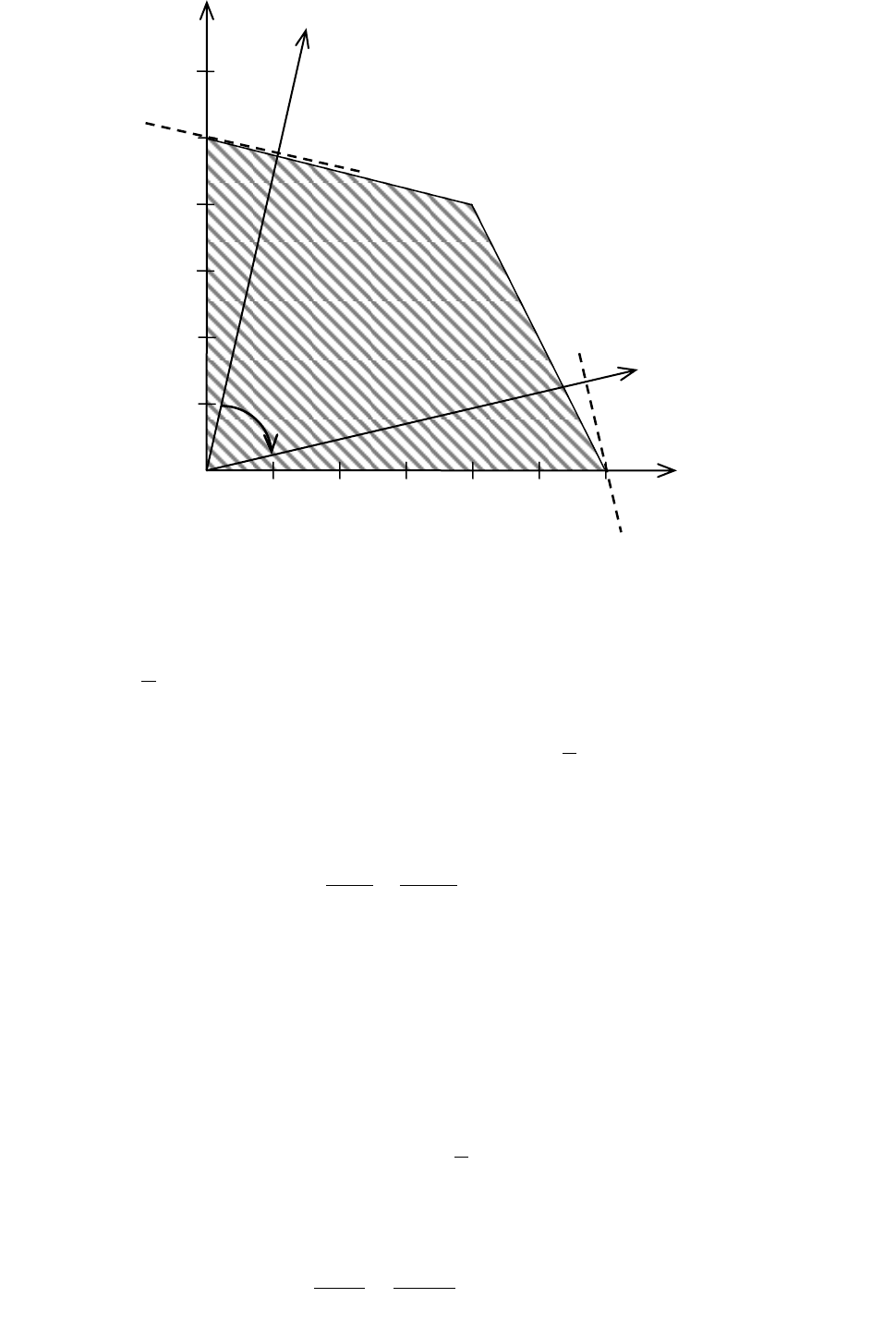
Чтобы найти решение задачи, построим многоугольник решений
(рис. 15), определяемый системой ограничений:
.0,0
,122
,204
21
21
21
xx
xx
xx
109
Рис. 15
Пусть t = 0. Найдѐм решение задачи F = 3x
1
+ 13x
2
max. Пере-
мещая прямую 3x
1
+ 13x
2
= a в направлении еѐ вектора нормали –
градиента
)13;3(n
, получаем X* = A(0; 5), F
max
= 0·3 + 5·13 = 65.
Из рис. 15 видно, что план X* = A(0; 5), F
max
= 65 будет оставаться
оптимальным для всякого t, пока вектор
)13;3( ttn
не станет
перпендикулярен прямой x
1
+ 4x
2
= 20 (1), то есть пока не будет вы-
полнено соотношение:
4
13
1
3 tt
t = 1/5.
Таким образом, для
5/1;0t
задача имеет оптимальный план
X* = A(0; 5), F
max
= 65 – 5t.
При t = 1/5 координаты любой точки отрезка AB дают оптималь-
ный план задачи, то есть X* = (0; 5) + (1–)(4; 4) = (4 – 4; 4+),
[0; 1], и F
max
= 64.
Если t > 1/5, то план X* = B(4; 4), F
max
= 64 будет оставаться опти-
мальным до тех пор, пока вектор
)13;3( ttn
не станет перпен-
дикулярным прямой 2x
1
+ x
2
= 12 (2), то есть пока не будет выпол-
нено соотношение
1
13
2
3 tt
t = 23/3.
0 1 2 3 4 5 6
6
5
4
3
2
1
B
A
x
1
x
2
(1)
(2)
t = 0
t = 10
C
