Кирсанова О.В., Семёнова Г.А. Математическое программирование (типовой расчёт)
Подождите немного. Документ загружается.


110
Таким образом, для
)3/23;5/1(t
задача имеет оптимальный план
X* = B(4; 4), F
max
= 64.
При t = 23/3 координаты любой точки отрезка BC дают оптималь-
ный план задачи, то есть X* = (4; 4) + (1 – )(6; 0) = (6 – 2; 4),
[0; 1], и F
max
= 64.
Если же 23/3 < t 10, то оптимальным является план X* = C(6; 0),
F
max
= 18 + 6t.
Ответ:
если
5/1;0t
, то X* = (0; 5), F
max
= 65,
если t = 1/5, то X* = (4–4; 4+), [0; 1], F
max
= 64,
если
3/23;5/1t
, то X* = (4; 4), F
max
= 64,
если t = 23/3, то X* = (6–2; 4), [0; 1], F
max
= 64,
если
10;3/23t
, то X* = (6; 0), F
max
= 18 + 6t.
Задача 3. Найдите решение задачи параметрического программи-
рования графическим методом.
3.1.
12
12
12
12
1 10 max;
2 12,
4 3 28;
0, 0;
0;9 .
F t x t x
xx
xx
xx
t
3.2.
12
12
12
12
4 15 max;
2 5 30,
4 3 32;
0, 0;
0;14 .
F t x t x
xx
xx
xx
t
3.3.
12
12
12
12
2 13 max;
3 5 35,
2 14;
0, 0;
0;12 .
F t x t x
xx
xx
xx
t
3.4.
12
12
12
12
1 11 max;
3 4 32,
5 2 30;
0, 0;
0;9 .
F t x t x
xx
xx
xx
t
3.5.
12
12
12
12
4 17 max;
4 24,
5 3 35;
0, 0;
0;16 .
F t x t x
xx
xx
xx
t
3.6.
12
12
12
12
3 12 max;
3 5 40,
5 30;
0, 0;
0;11 .
F t x t x
xx
xx
xx
t

111
3.7.
12
12
12
12
2 15 max;
5 30,
5 2 35;
0, 0;
0;14 .
F t x t x
xx
xx
xx
t
3.8.
12
12
12
12
4 19 max;
3 21,
5 35;
0, 0;
0;18 .
F t x t x
xx
xx
xx
t
3.9.
12
12
12
12
3 17 max;
2 16,
5 2 40;
0, 0;
0;16 .
F t x t x
xx
xx
xx
t
3.10.
12
12
12
12
1 14 max;
4 7 63,
5 40;
0, 0;
0;13 .
F t x t x
xx
xx
xx
t
3.11.
12
12
12
12
2 19 max;
2 7 49,
5 3 50;
0, 0;
0;18 .
F t x t x
xx
xx
xx
t
3.12.
12
12
12
12
1 9 max;
2 16,
3 18;
0, 0;
0;8 .
F t x t x
xx
xx
xx
t
3.13.
12
12
12
12
3 13 max;
3 4 36,
2 14;
0, 0;
0;12 .
F t x t x
xx
xx
xx
t
3.14.
12
12
12
12
2 16 max;
5 35,
3 2 27;
0, 0;
0;15 .
F t x t x
xx
xx
xx
t
3.15.
12
12
12
12
4 20 max;
3 5 45,
3 21;
0, 0;
0;19 .
F t x t x
xx
xx
xx
t
3.16.
12
12
12
12
3 17 max;
2 7 42,
4 3 40;
0, 0;
0;16 .
F t x t x
xx
xx
xx
t
3.17.
12
12
12
12
1 14 max;
3 7 49,
2 18;
0, 0;
0;13 .
F t x t x
xx
xx
xx
t
3.18.
12
12
12
12
2 15 max;
2 7 56,
6 5 72;
0, 0;
0;13 .
F t x t x
xx
xx
xx
t

112
3.19.
12
12
12
12
3 22 max;
7 49,
2 20;
0, 0;
0;20 .
F t x t x
xx
xx
xx
t
3.20.
12
12
12
12
4 25 max;
6 42,
3 2 30;
0, 0;
0;24 .
F t x t x
xx
xx
xx
t
3.21.
12
12
12
12
2 19 max;
3 24,
12;
0, 0;
0;18 .
F t x t x
xx
xx
xx
t
3.22.
12
12
12
12
1 15 max;
3 18,
2 16;
0, 0;
0;14 .
F t x t x
xx
xx
xx
t
3.23.
12
12
12
12
2 11 max;
4 16,
3 2 18;
0, 0;
0;10 .
F t x t x
xx
xx
xx
t
3.24.
12
12
12
12
3 9 max;
2 10,
3 15;
0, 0;
0;8 .
F t x t x
xx
xx
xx
t
3.25.
12
12
12
12
1 7 max;
5 20,
8;
0, 0;
0;6 .
F t x t x
xx
xx
xx
t
3.26.
12
12
12
12
4 12 max;
3 5 30,
3 18;
0, 0;
0;11 .
F t x t x
xx
xx
xx
t
3.27.
12
12
12
12
3 10 max;
2 12,
3 2 24;
0, 0;
0;9 .
F t x t x
xx
xx
xx
t
3.28.
12
12
12
12
2 14 max;
6 24,
3 21;
0, 0;
0;13 .
F t x t x
xx
xx
xx
t
3.29.
12
12
12
12
1 8 max;
2 7 35,
3 2 27;
0, 0;
0;7 .
F t x t x
xx
xx
xx
t
3.30.
12
12
12
12
4 13 max;
3 7 42,
3 24;
0, 0;
0;12 .
F t x t x
xx
xx
xx
t
113
3.31.
12
12
12
12
3 13 max;
4 20,
2 12;
0, 0;
0;10 .
F t x t x
xx
xx
xx
t
Упражнение 4. Найдите решение задачи параметрического про-
граммирования симплексным методом.
.0,0
,3025
,3243
max,11)1(
21
21
21
21
xx
xx
xx
xxtF
Решение.
Решим задачу симплекс-методом (подробно этот метод был опи-
сан в упражнении 2, глава 1). Для этого приведем задачу к канониче-
скому виду:
.0,0,0,0
,3025
,3243
max,11)1(
4321
421
321
21
xxxx
xxx
xxx
xxtF
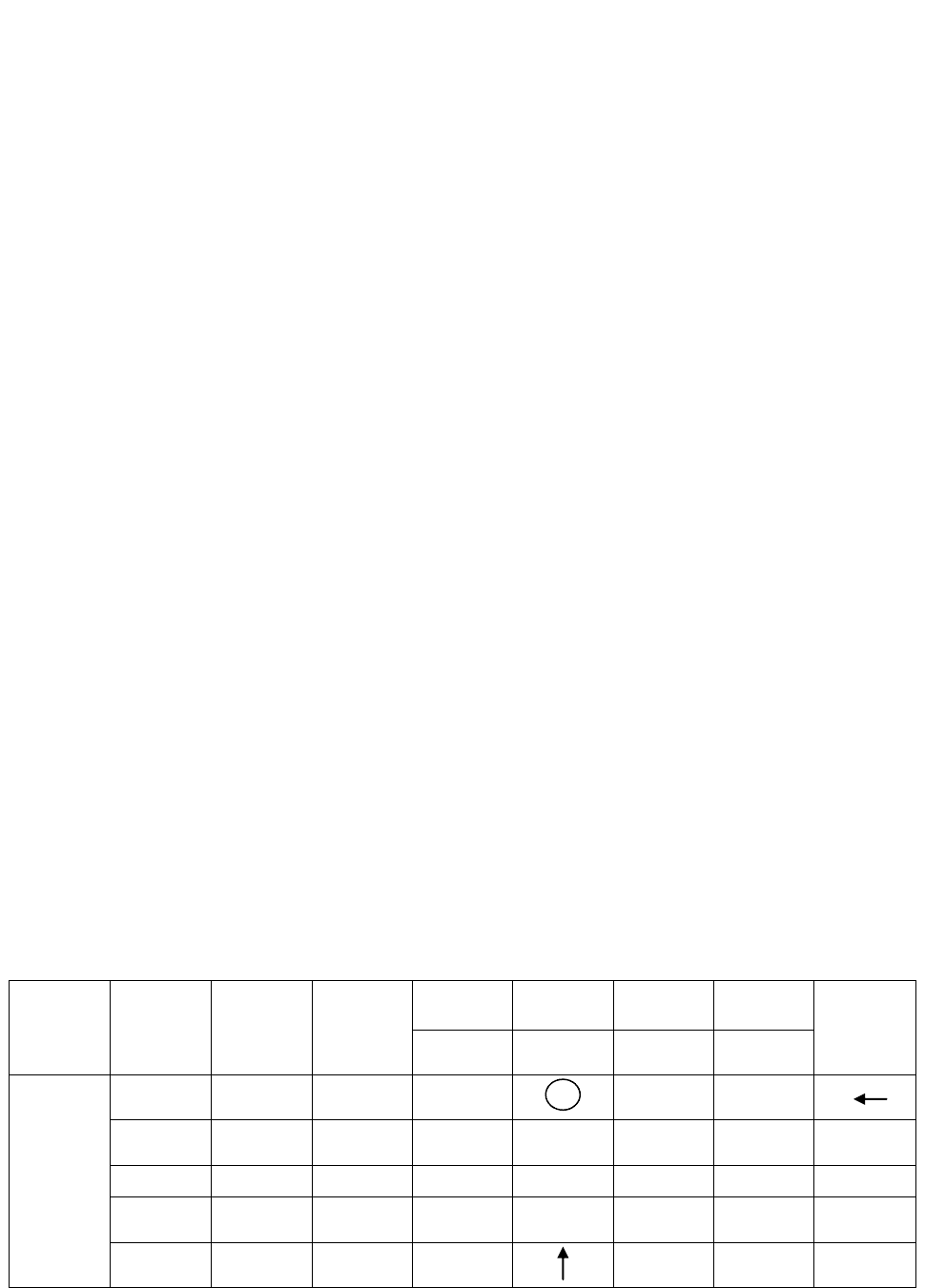
Внесѐм данные задачи в симплекс-таблицу 82.
Таблица 82
План
Базис
С
б
b
i
1+t
11
0
0
d
i
x
1
x
2
x
3
x
4
I
x
3
0
32
3
4
1
0
8
x
4
0
30
5
2
0
1
15
F
=
0
–1–t
–11
0
0
Базисным решением в таком случае будет X
1
= (0; 0; 32; 30), при
котором целевая функция будет F равна 0, то есть F
1
= 0.
114
Для базисного решения X
1
критерий оптимальности не выполнен,
так как в столбце, соответствующем свободной переменной x
2
, в це-
левой функции есть отрицательный элемент (–11). Чтобы перейти к
построению плана II, нужно перевести переменную x
2
в базис, а ба-
зисную переменную x
3
– в свободные.
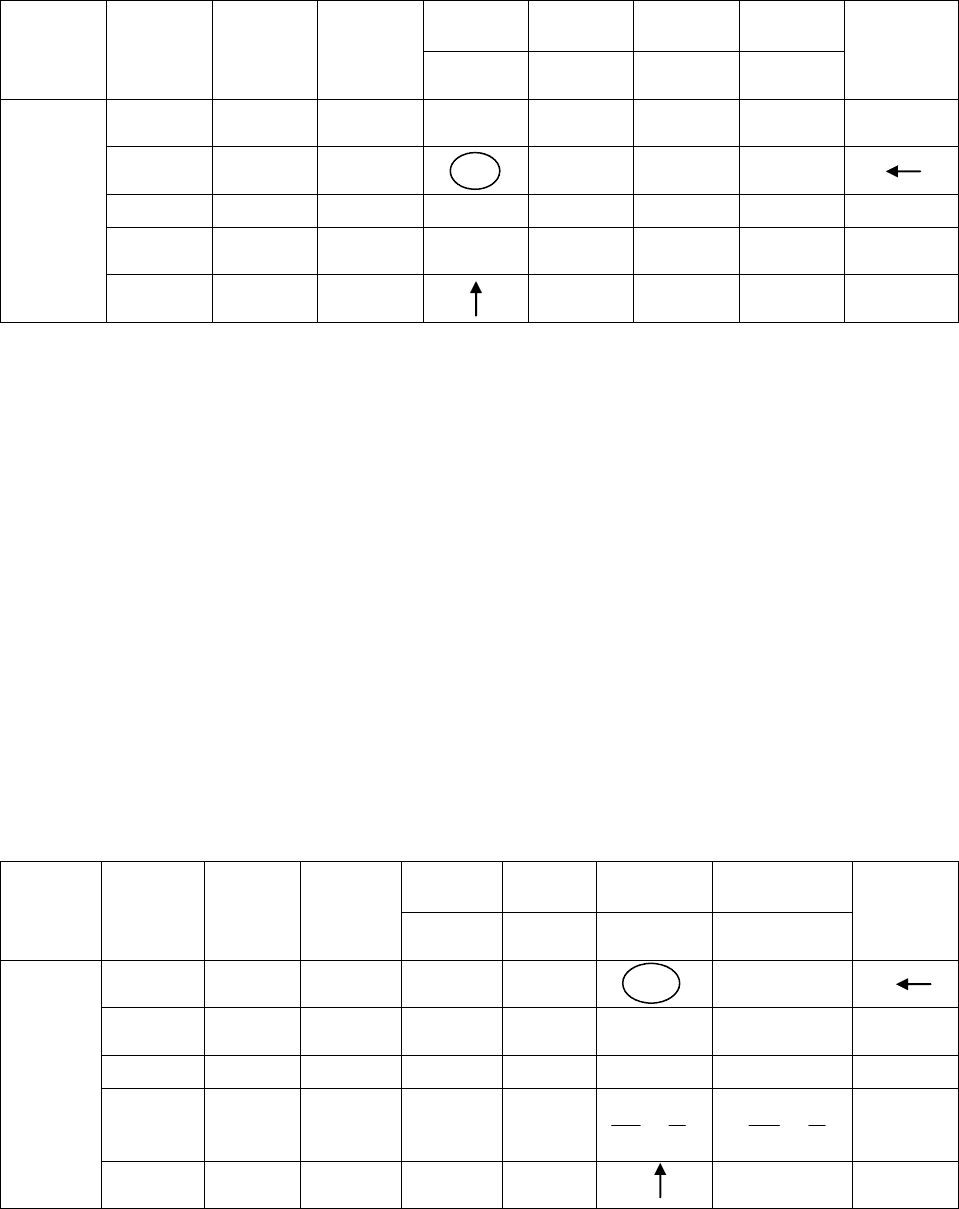
Вычисляем элементы новой симплекс-таблицы 83.
Таблица 83
План
Базис
С
б
b
i
1+t
11
0
0
d
i
x
1
x
2
x
3
x
4
II
x
2
11
8
3/4
1
1/4
0
32/3
x
4
0
14
7/2
0
–1/2
1
4
F
=
88
29/4–t
0
11/4
0
Базисным решением в таком случае будет X
2
= (0; 8; 0; 14), при
котором целевая функция будет F равна 88, то есть F
2
= 88.
Для базисного решения X
2
при проверке критерия оптимальности
возможны три случая:
а) 29/4 – t > 0 t < 29/4, тогда решение X
2
является оптималь-
ным и единственным;
б) 29/4 – t = 0 t = 29/4, тогда решение X
2
является оптималь-
ным, но не единственным, и следует продолжать поиск;
в) 29/4 – t < 0 t > 29/4, тогда решение X
2
не оптимальное, и
поиск решения продолжается.
Чтобы в случаях б) и в) перейти к построению плана III, нужно
перевести переменную x
1
в базис, а базисную переменную x
4
– в сво-
бодные.
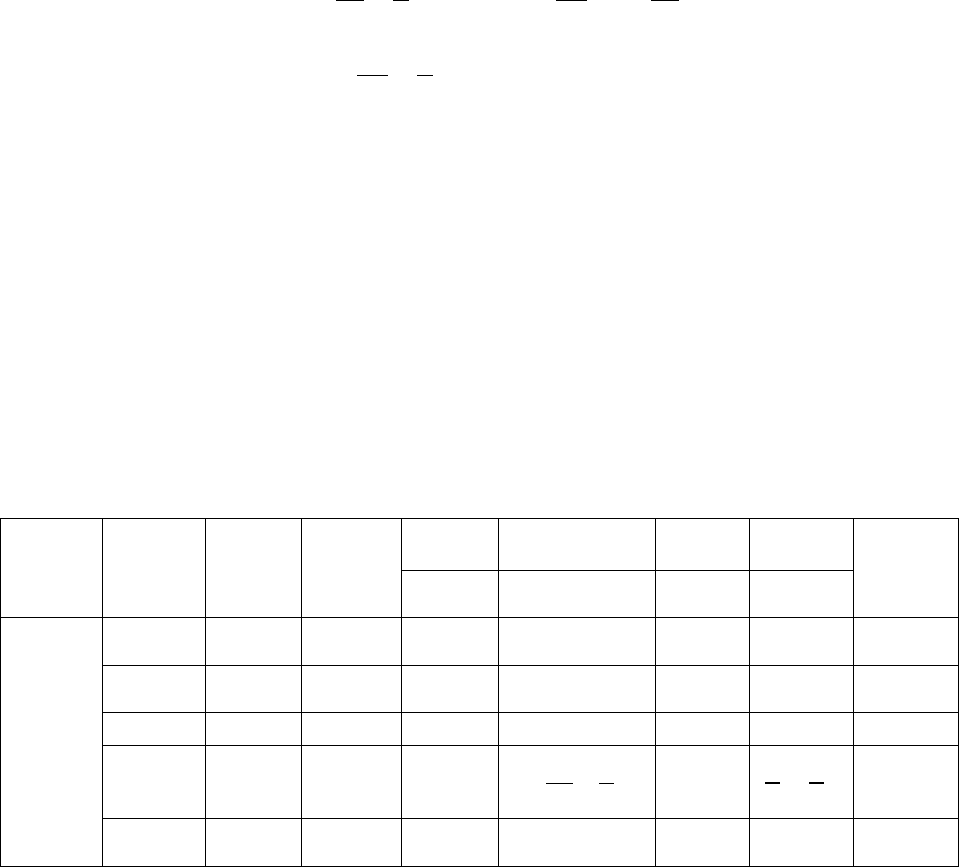
Вычисляем элементы новой симплекс-таблицы 84.
Таблица 84
План
Базис
С
б
b
i
1+t
11
0
0
d
i
x
1
x
2
x
3
x
4
III
x
2
11
5
0
1
5/14
–3/14
14
x
1
1+t
4
1
0
–1/7
2/7
F
=
59+4t
0
0
t
7
1
14
53
t
7
2
14
29
115
Базисным решением в таком случае будет X
3
= (4; 5; 0; 0), при ко-
тором целевая функция будет F равна (59+4t), то есть F
3
= 59+4t.
Для базисного решения X
3
при проверке критерия оптимальности
возможны четыре случая:
а) t = 29/4, тогда решение X
3
является оптимальным, но не единст-
венным. Общий вид оптимального решения можно записать:
X* = (0; 8; 0; 14) + (1–)(4; 5; 0; 0) = (4–4; 5+3; 0; 14),
[0; 1], при этом F
max
= 88;
б)
2
53
4
29
,0
7
2
14
29
,0
7
1
14
53
,4/29
t
t
t
t
,
тогда решение X
3
является оптимальным и единственным;
в) 53/14 – 1/7·t = 0 t = 53/2, тогда решение X
3
является опти-
мальным, но не единственным, и следует продолжать поиск решения;
г) t > 53/2, тогда решение X
3
не оптимальное, и поиск решения
продолжается.
Чтобы в случаях в) и г) перейти к построению плана IV, нужно
перевести переменную x
3
в базис, а базисную переменную x
2
– в сво-
бодные.
Вычисляем элементы новой симплекс-таблицы 85.
Таблица 85
План
Базис
С
б
b
i
1+t
11
0
0
d
i
x
1
x
2
x
3
x
4
IV
x
3
0
14
0
14/5
1
–3/5
x
1
1+t
6
1
2/5
0
1/5
F
=
6+6t
0
t
5
2
5
53
1
t
5
1
5
1
Базисным решением в таком случае будет X
4
= (6; 0; 14; 0), при
котором целевая функция будет F равна (6 + 6t), то есть F
4
= 6 + 6t.

116
Для базисного решения X
4
при проверке критерия оптимальности
возникают два случая:
а) t = 53/2, тогда решение X
4
является оптимальным, но не единст-
венным. Общий вид оптимального решения можно записать:
X* = (4; 5; 0; 0) + (1– )(6; 0; 14; 0) = (6 – 2; 5; 14 – 14; 0),
[0; 1], при этом F
max
= 165;
б)
,
2
53
,0
5
1
5
1
,0
5
2
5
53
,2/53
t
t
t
t
тогда решение X
4
является оптимальным и единственным.
Ответ:
если
)4/29;(t
, то X* = (0; 8; 0; 14), F
max
= 88,
если t = 29/4, то X* = (4–4; 5+3; 0; 14), [0; 1], F
max
= 88,
если
2/53;4/29t
, то X* = (4; 5; 0; 0), F
max
= 59 + 4t,
если t = 53/2, то X* = (6–2; 5; 14–14; 0), [0; 1], F
max
= 165,
если
;2/53t
, то X* = (6; 0; 14; 0), F
max
= 6 + 6t.
Задача 4. Найдите решение задачи параметрического программи-
рования симплексным методом.
4.1.
12
12
12
12
3 13 max;
4 20,
2 12;
0, 0.
F t x x
xx
xx
xx
4.2.
12
12
12
12
14 max;
3 7 49,
2 18;
0, 0.
F x t x
xx
xx
xx
4.3.
12
12
12
12
2 15 max;
5 30,
5 2 35;
0, 0.
F t x x
xx
xx
xx
4.4.
12
12
12
12
4 19 max;
3 21,
5 35;
0, 0.
F x t x
xx
xx
xx

117
4.5.
12
12
12
12
3 17 max;
2 16,
5 2 40;
0, 0.
F t x x
xx
xx
xx
4.6.
12
12
12
12
14 max;
4 7 63,
5 40;
0, 0.
F x t x
xx
xx
xx
4.7.
12
12
12
12
2 max;
2 7 49,
5 3 50;
0, 0.
F t x x
xx
xx
xx
4.8.
12
12
12
12
9 max;
2 16,
3 18;
0, 0.
F x t x
xx
xx
xx
4.9.
12
12
12
12
3 13 max;
3 4 36,
2 14;
0, 0.
F t x x
xx
xx
xx
4.10.
12
12
12
12
2 16 max;
5 35,
3 2 27;
0, 0.
F x t x
xx
xx
xx
4.11.
12
12
12
12
4 20 max;
3 5 45,
3 21;
0, 0.
F t x x
xx
xx
xx
4.12.
12
12
12
12
3 17 max;
2 7 42,
4 3 40;
0, 0.
F x t x
xx
xx
xx
4.13.
12
12
12
12
2 15 max;
2 7 56,
6 5 72;
0, 0.
F t x x
xx
xx
xx
4.14.
12
12
12
12
15 max;
3 18,
2 16;
0, 0.
F x t x
xx
xx
xx
4.15.
12
12
12
12
3 22 max;
7 49,
2 20;
0, 0.
F t x x
xx
xx
xx
4.16.
12
12
12
12
3 9 max;
2 10,
3 15;
0, 0.
F x t x
xx
xx
xx
4.17.
12
12
12
12
2 19 max;
3 24,
12;
0, 0.
F t x x
xx
xx
xx
4.18.
12
12
12
12
4 12 max;
3 5 30,
3 18;
0, 0.
F x t x
xx
xx
xx

118
4.19.
12
12
12
12
2 11 max;
4 16,
3 2 18;
0, 0.
F t x x
xx
xx
xx
4.20.
12
12
12
12
2 14 max;
6 24,
3 21;
0, 0.
F x t x
xx
xx
xx
4.21.
12
12
12
12
1 7 max;
5 20,
8;
0, 0.
F t x x
xx
xx
xx
4.22.
12
12
12
12
4 13 max;
3 7 42,
3 24;
0, 0.
F x t x
xx
xx
xx
4.23.
12
12
12
12
3 10 max;
2 12,
3 2 24;
0, 0.
F t x x
xx
xx
xx
4.24.
12
12
12
12
10 max;
2 12,
4 3 28;
0, 0.
F x t x
xx
xx
xx
4.25.
12
12
12
12
1 8 max;
2 7 35,
3 2 27;
0, 0.
F t x x
xx
xx
xx
4.26.
12
12
12
12
2 13 max;
3 5 35,
2 14;
0, 0.
F x t x
xx
xx
xx
4.27.
12
12
12
12
4 25 max;
6 42,
3 2 30;
0, 0.
F t x x
xx
xx
xx
4.28.
12
12
12
12
4 17 max;
4 24,
5 3 35;
0, 0.
F x t x
xx
xx
xx
4.29.
12
12
12
12
4 15 max;
2 5 30,
4 3 32;
0, 0.
F t x x
xx
xx
xx
4.30.
12
12
12
12
3 12 max;
3 5 40,
5 30;
0, 0.
F x t x
xx
xx
xx
4.31.
12
12
12
12
1 11 max;
3 4 32,
5 2 30;
0, 0.
F t x x
xx
xx
xx
119
Упражнение 5. Найдите решение задачи параметрического про-
граммирования симплексным методом.
.13;34
,0,0
,142
,3553
max,23
21
21
21
21
t
xx
txx
txx
xxF
Решение.
Решим задачу симплекс-методом. Для этого приведем задачу к
каноническому виду:
.13;34
,0,0,0,0
,142
,3553
max,23
4321
421
321
21
t
xxxx
txxx
txxx
xxF
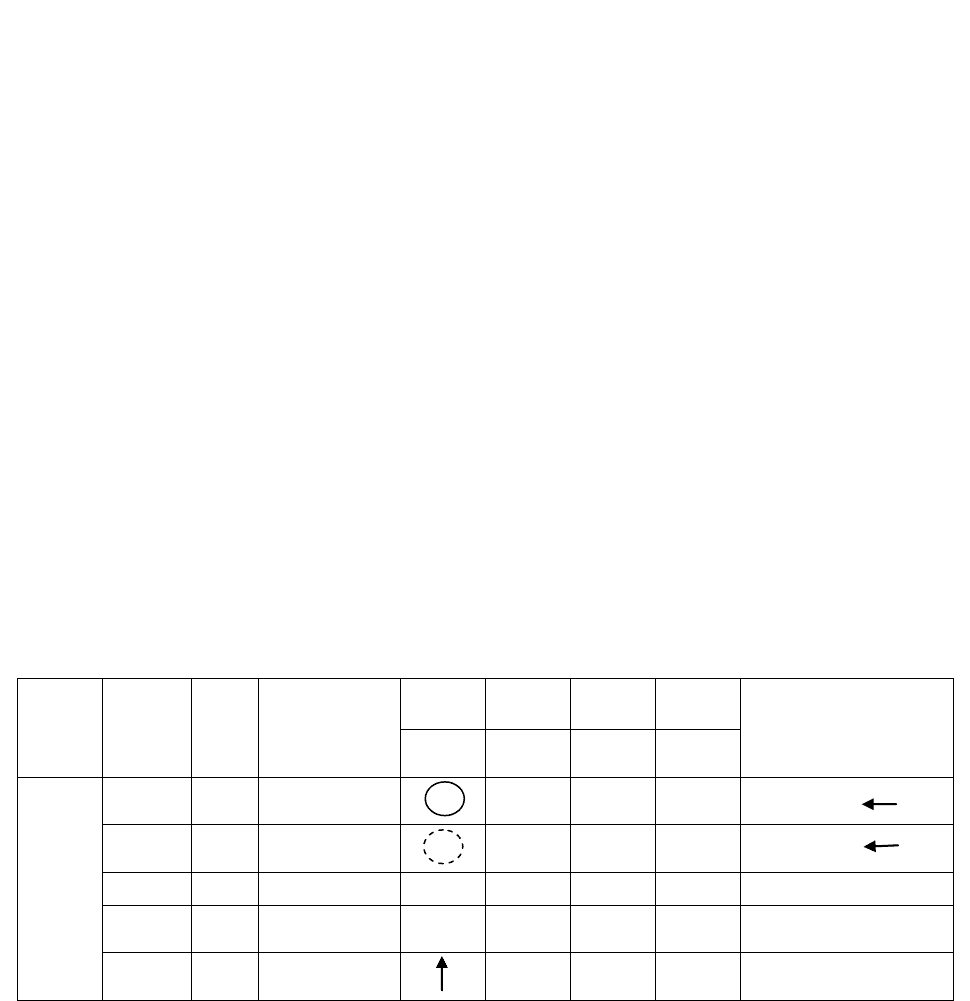
Внесѐм данные задачи в симплекс-таблицу 86.
Таблица 86
План
Базис
С
б
b
i
3
2
0
0
d
i
x
1
x
2
x
3
x
4
I
x
3
0
35 – t
3
5
1
0
35/3+1/3t II
x
4
0
14 – t
2
1
0
1
7–1/2t II
F
=
0
–3
–2
0
0
Базисным решением в таком случае будет X
1
= (0; 0; 35 – t; 14 – t),
при котором целевая функция будет F равна 0, то есть F
1
= 0.
Для базисного решения X
1
критерий оптимальности не выполнен,
так как в целевой функции есть отрицательные элементы. Чтобы пе-
рейти к построению плана II, нужно перевести переменную x
1
в базис.
При выборе базисной переменной, которую нужно перевести в
свободные, возможны два случая:
а)
1334
,2/173/13/35
t
tt
–34 t –28/5, тогда в свободные пе-
реводим переменную x
3
(план II);
