King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

where x

and x ∈ [a, b], f

(x) is a ﬁr st-order derivative of f (x), f ″(x) is a second-order

derivative of f (x) and so on. The Taylor expansion for e

can be derived by setting

f (x)=e

and expanding this function about x

= 0 using the Taylor series. The

Taylor series repres entation of functions is an extremely useful tool for approxima-

ting functions and thereby deriving numerical methods of solution. Because the

series is inﬁnite, only a ﬁnite number of initial terms can be retained for approxima-

ting the solution. The higher-order terms usually contribute negligibly to the ﬁnal

sum and can be justiﬁably discarded. Often, series approximations of functions

require only the ﬁrst few terms to generate the desired accuracy. In other words,

the series is truncated, and the error in the approximation depends on the discarded

terms and is called the truncation error. The Taylor series truncated to the nth order

term can exactly represent an nth-order polynomial. However, an inﬁnite Taylor

series is required to converge exactly to a non-polynomial function.

Since the function value is known at x

and we are trying to obtain the function

value at x, the difference, x – x

, is called the step size, which we denote as the

independent variable h. As you will see, the step size plays a key role in determining

both the truncation error and the round-off error in the ﬁnal solution. Let’s rewrite

the Taylor series expansion in terms of the powers of h:

fxðÞ¼fx

ðÞþf

ðÞh þ

ðÞh

000

ðÞh

þþ

ðÞh

þ: (1:12)

As the step size h is gradually decreased when evaluating f (x), the higher-order terms

are observed to diminish much faster than the lower-order terms due to the dependency

of the higher-order terms on larger powers of h.ThisisdemonstratedinExamples 1.10

and 1.11. We can list two possible methods to reduce the truncation error:

(1) reduce the step size h, and/or

(2) retain as many terms as possible in the series approximation of the function.

While both these possibilities will reduce the truncation error, they can increase the

round-off error. As h is decreased, the higher-order terms greatly diminish in value.

This can lead to the addition operation of small numbers to large numbers or

subtractive cancellation, especially in an alternating series in which some terms are

added while others are subtracted such as in the following sine series:

sin x ¼ x 



þ: (1:13)

One way to curtail loss in accuracy due to addition of large quantities to small

quantities is to sum the small terms ﬁrst, i.e. sum the terms in the series backwards.

Reducing the step size is usually synonymous with an increased number of

computational steps: more steps must be “climbed” before the desired function

value at x is obtained. Increased computations, either due to reduction in step size

or increased number of terms in the series, will generally increase the round-off error.

There is a trade-off between reducing the truncation error and limiting the round-off error, despite the

fact that these two sources of error are independent from each other in origin.

We will explore the nature and implications of these two error types when

evaluating functions numerically in the next few examples.

The Taylor series can be rewritten as a ﬁnite series with a remainder term R

þ hðÞ¼fx

ðÞþf

ðÞh þ

ðÞh

000

ðÞh

þþ

ðÞh

þ R

(1:14)

1.6 Taylor series and truncation error

and

nþ1

ξðÞh

nþ1

ðn þ 1Þ!

; ξE x

; x

þ h½: (1:15)

The remainder term R

is generated when the (n + 1)th and higher-order terms are

discarded from the series. The value of ξ is generally not known. Of course, if R

could be determined exactly, it could be easily incorporated into the numerical

algorithm and then there would unquestionably be no truncation error! When

using truncated series representations of functions for solving numerical problems,

it is beneﬁcial to have, at the least, an order of magnitude estimate of the error

involved, and the (n + 1)th term serves this purpose.

1.6.1 Order of magnitude estimation of truncation error

As mentioned earlier, the order of magnitude of a quantity provides a rough estimate

of its size. A number p that is of order of magni tude 1, is written as p ∼ O(1).

Knowledge of the order of magnitude of various quantities involved in a given

problem highlights quantities that are important and those that are comparatively

small enough to be neglected. The utility of an order of magnitude estimate of the

truncation error inherent in a numerical algorithm is that it allows for comparison of

the size of the error with respect to the solution.

If the function jf

nþ1

xðÞjin Equation (1.15) has a maximum value of K for x

≤ x ≤

+ h, then

nþ1

ξðÞh

nþ1

n þ 1ðÞ!



Kjhj

nþ1

n þ 1ðÞ!

 Oh

nþ1



: (1:16)

The error term R

is said to be of order h

nþ1

or Oh

nþ1



. Although the multipliers

K and 1/( n+1)! inﬂuence the overall magnitude of the error, because they are

constants they do not change as h is varied and hence are not as important as the

“power of h” t erm when assessing the effects of s tep size or w hen comparing

different algorithms. By expressing the error term as a power of h, the rate of

decay of the error term with change in step size is conveyed. Truncation errors of

higher orders of h decay much faster when the step size is halved compared with

those of lower orders. For example, if the Taylor series approximation contains

only the ﬁrst two terms, then t he error term, T

,is∼O(h

). If two different step

sizes are used, h and h/2, then the magnitude of the truncation errors can be

compared as follows:

E;h=2

E;h

ðh=2Þ

ðhÞ

Note that when the step size h is halved the error is reduced to one-quarter of the

original error.

Example 1.9 Estimation of round-off errors in the e

−x

series

Using the Taylor series expansion for f (x)=e

−x

about x

= 0, we obtain

x

¼ 1  x þ



þ: (1:17)

Types and sources of numerical error

For the purpose of a simplified estimation of the round-off error inherent in computing this series, assume

that each term has associated with it an error E of 10

–8

times the magnitude of that term (single-precision

arithmetic). Since round-off errors in addition and subtraction operations are additive, the total error due to

summation of the series is given by

error ¼ E  1 þ E  x þ E 

þ E 

þ¼E  e

The sum of the series inclusive of error is

x

¼ e

x

 E  e

¼ e

x

1  E  e



If the magnitude of x is small, i.e. 0 < x < 1, the error is minimal and therefore constrained. However, if

x ∼ 9, the error E  e

becomes O(1)! Note that, in this algorithm, no term has been truncated from the

series, and, by retaining all terms, it is ensured that the series converges exactly to the desired limit for all x.

However, the presence of round-off errors in the individual terms produces large errors in the final solution

for all x ≥ 9. How can we avoid large round-off errors when summing a large series? Let’s rewrite Equation

(1.17) as follows:

x

1 þ

þ

The solution inclusive of round-off error is now

 E  e

x

1  E

The error is now of O(ε) for all x >0.

Example 1.10 Exploring truncation errors using the Taylor series representation for e

−x

The Taylor series expansion for f (x)=e

−x

is given in Equation (1.17). A MATLAB program is written to

evaluate the sum of this series for a user-specified value of x using n terms. The danger of repeated

multiplications either in the numerator or denominator, as demonstrated in Box 1.3, can lead to fatal

overflow errors. This problematic situation can be avoided if the previous term is used as a starting point

to compute the next term. The MATLAB program codes for a function called taylorenegativex

that requires input of two variables x and n. A MATLAB function that requires input variables must be

run from the Command Window, by typing in the name of the function along with the values of the

input parameters within parentheses after the function name. This MATLAB function is used to

approximate the function e

−x

for two values of x: 0.5 and 5. A section of the code in this program serves

the purpose of detailing the appearance of the graphical output. Plotting functions are covered in

Appendix A.

MATLAB program 1.3

function taylorenegativex(x, n)

% This function calculates the Taylor series approximation for e^-x for 2

% to n terms and determines the improvement in accuracy with the addition

% of each term.

% Input Variables

% x is the function variable

% n is the maximum number of terms in the Taylor series

% Only the positive value of x is desired

1.6 Taylor series and truncation error

if (x < 0)

x = abs(x);

end

% Additional Variables

term = 1; % ﬁ rst term in the series

summation(1) = term; % summation term

enegativex = exp(-x); % true value of e^-x

err(1) = abs(enegativex - summation(1));

fprintf(‘ n Series sum Absolute error Percent relative error\n’)

for i = 2:n

term = term*(-x)/(i-1);

summation = summation + term;

(% Absolute error after addition of each term)

err(i) = abs(summation - enegativex);

fprintf(‘%2d %14.10f %14.10f %18.10f\n’,i, sum,err(i),err(i)/...

enegativex*100)

end

plot([1:n], err, ‘k-x’,‘LineWidth’,2)

xlabel(‘Number of terms in e^-^x series’,‘FontSize’,16)

ylabel(‘Absolute error’ , ‘ FontSize’,16)

title([‘Truncation error changes with number of terms, x =’,num2str

(x)],...‘FontSize’,14)

set(gca,‘FontSize’,16,‘LineWidth’,2)

We type the following into the Command Window:

taylorenegativex(0.5, 12)

MATLAB outputs:

n Series sum Absolute error Percent relative error

2 2.0000000000 0.1065306597 17.5639364650

3 1.6000000000 0.0184693403 3.0450794188

4 1.6551724138 0.0023639930 0.3897565619

5 1.6480686695 0.0002401736 0.0395979357

6 1.6487762988 0.0000202430 0.0033375140

7 1.6487173065 0.0000014583 0.0002404401

8 1.6487215201 0.0000000918 0.0000151281

9 1.6487212568 0.0000000051 0.0000008450

10 1.6487212714 0.0000000003 0.0000000424

11 1.6487212707 0.0000000000 0.0000000019

12 1.6487212707 0.0000000000 0.0000000001

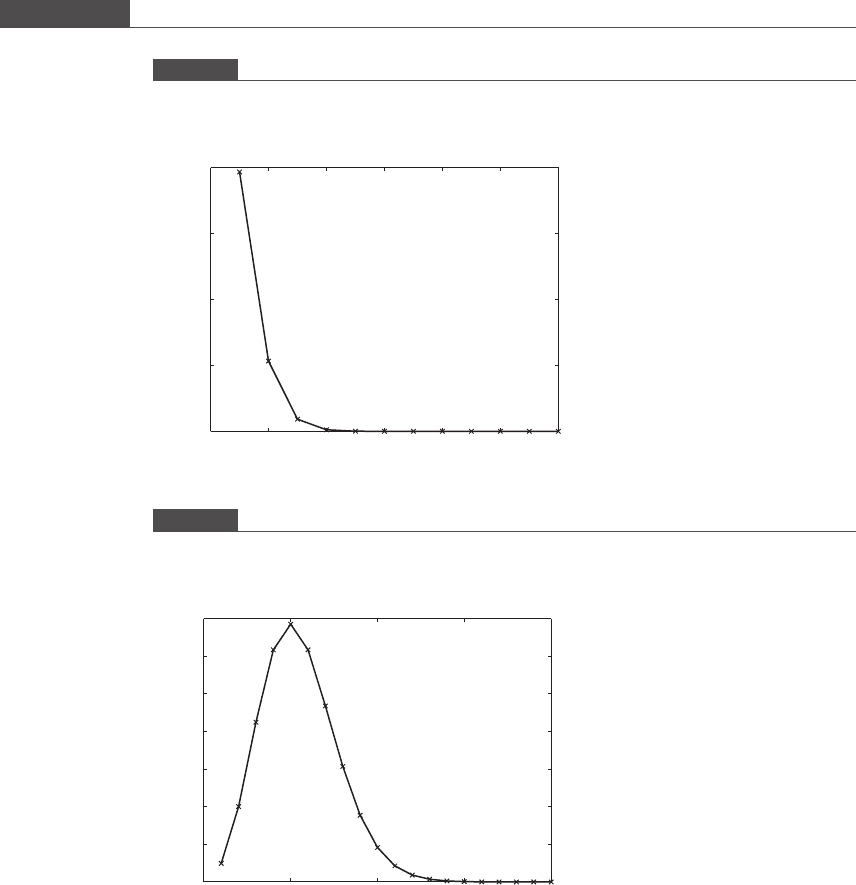
and draws Figure 1.4.

The results show that by keeping only three terms in the series, the error is

reduced to ∼3%. By including 12 terms in the series, the absolute error becomes

less than 10

–10

and the relative error is O(10

–12

). Round-off error does not play

a role until we begin to consider errors on the order of 10

–15

, and this magnitude

is of course too small to be of any importance w hen considering the absolute value

of e

−0.5

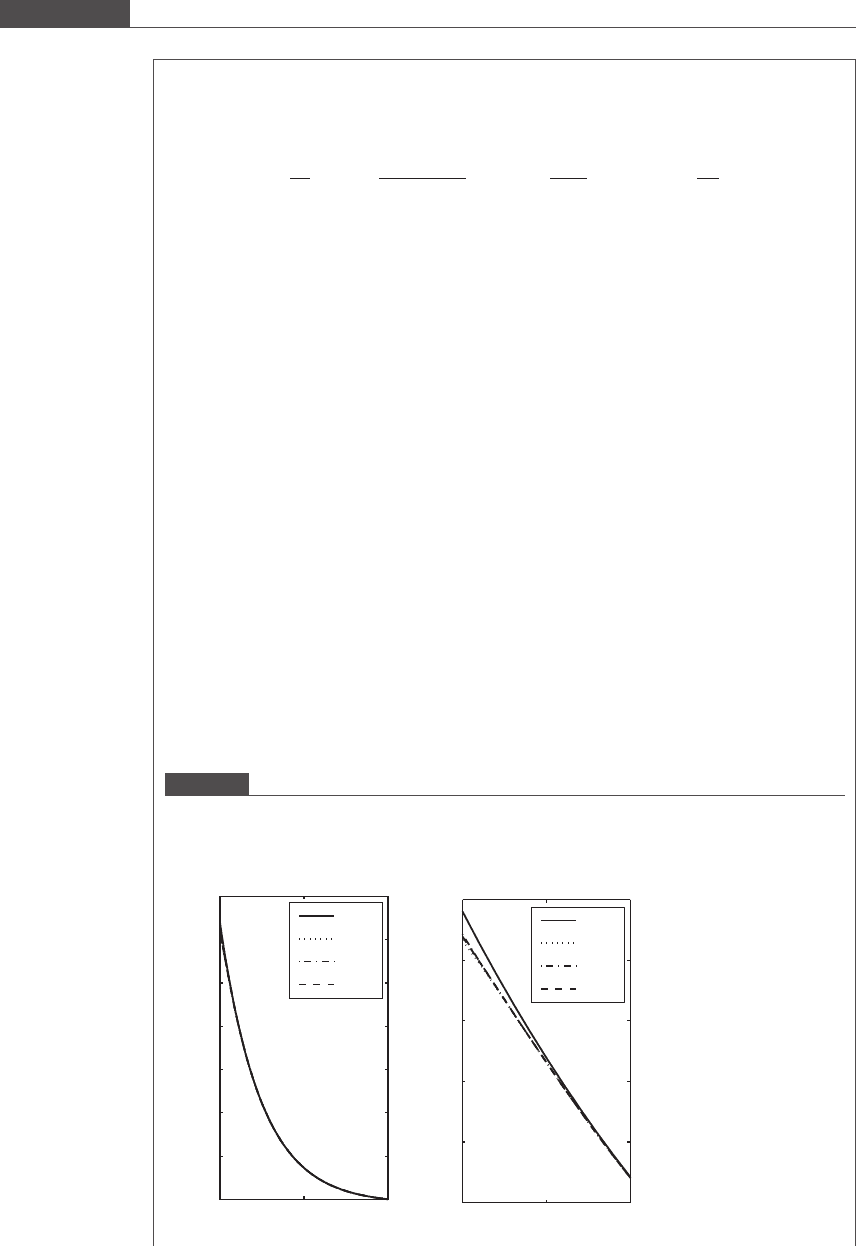
Repeating this exercise for x = 5, we obtain the following tabulated results and

Figure 1.5.

Types and sources of numerical error

 taylorenegativex(5,20)

n Series sum Absolute error Percent relative error

2 −4.0000000000 4.0067379470 59465.2636410306

3 8.5000000000 8.4932620530 126051.1852371901

4 −12.3333333333 12.3400712803 183142.8962265111

5 13.7083333333 13.7015953863 203349.7056031154

6 −12.3333333333 12.3400712803 183142.8962265111

7 9.3680555556 9.3613176086 138934.2719648443

8 −6.1329365079 6.1396744549 91120.8481718382

9 3.5551835317 3.5484455847 52663.6019135884

10 −1.8271053792 1.8338433262 27216.6481338708

11 0.8640390763 0.8573011293 12723.4768898588

12 −0.3592084035 0.3659463505 5431.1253936547

Figure 1.4

Change in error with increase in number of terms in the negative exponential series for x = 0.5.

0 2 4 6 8 10 12

0.1

0.2

0.3

0.4

Number of terms in e

−x

series

Absolute error

Truncation error changes with number

of terms, x

= 0.5

Figure 1.5

Change in error with increase in number of terms in the negative exponential series for x =5.

0 5 10 15 20

Number of terms in e

−x

series

Absolute error

Truncation error changes with number

of terms, x

= 5

1.6 Taylor series and truncation error

13 0.1504780464 0.1437400994 2133.2922244759

14 −0.0455552035 0.0522931505 776.0991671128

15 0.0244566714 0.0177187244 262.9691870261

16 0.0011193798 0.0056185672 83.3869310202

17 0.0084122834 0.0016743364 24.8493558692

18 0.0062673118 0.0004706352 6.9848461571

19 0.0068631372 0.0001251902 1.8579877391

20 0.0067063411 0.0000316059 0.4690738125

For |x| > 1, the Taylor series is less efﬁcient in arriving at an approximate solution.

In fact, the approximation is worse when including the second through the tenth

term in the series than it is when only including the ﬁrst term (zeroth-order approx-

imation, i.e. the slope of the function is zero). The large errors that spawn from the

inclusion of additional terms in the series sum are due to the dramatic increase in the

numerator of these terms as compared to the growth of the denominator; this throws

the series sum off track until there are a sufﬁcient number of large terms in the sum to

cancel each other. The relative error is <5% only after the inclusion of 19 terms!

This example shows that a series such as this one which has alternating positive and

negative terms takes longer to converge than a strictly positive term series. This

brings us to the next topic: what is meant by the convergence of a series?

1.6.2 Convergence of a series

An inﬁnite series S is deﬁned as the sum of the terms in an inﬁnite sequence

; t

; ...; t

...; t

∞

. The sum of the ﬁrst n terms of an inﬁnite sequence is denoted

by S

.IfS tends to a ﬁnite limit as n, the number of terms in the series, tends to ∞,

then S is said to be a convergent series. A necessary (but not sufﬁcient) condition for

any convergent series is that lim

n!∞

¼ 0, or that

lim

n!∞

 S

n1

¼ 0:

There are a number of convergence tests that are formally used to determine whether

a series is co nvergent or divergent. When the series limit is not known, a simple

convergence condition used to determine if a convergent series has converged to

within tolerable error is

 S

n1

¼ t

 δ;

where δ is a positive constant an d speciﬁes some tolerance limit.

Example 1.10 shows that the Taylor series expansion converges rapidly for |x|<1

since the higher-order terms rapidly diminish. However, difﬁculties arise when we

use the e

−x

expansion for |x| > 1. Is there a way to rectify this problem?

Example 1.11 Alternate method to reduce truncation errors

As discussed earlier, it is best to minimize round-off errors by avoiding subtraction operations. This

technique can also be applied to Example 1.10 to resolve the difficulty in the convergence rate of the series

encountered for |x| > 1. Note that e

−x

can be rewritten as

x

1 þ

þ

After making the appropriate changes to MATLAB program 1.3, we rerun the function

taylorenegativex for x = 5 in the Command Window, and obtain

Types and sources of numerical error

 taylorenegativex(5,20)

n Series sum Absolute error Percent relative error

2 0.1666666667 0.1599287197 2373.5526517096

3 0.0540540541 0.0473161071 702.2332924464

4 0.0254237288 0.0186857818 277.3215909388

5 0.0152963671 0.0085584201 127.0182166005

6 0.0109389243 0.0042009773 62.3480318351

7 0.0088403217 0.0021023747 31.2020069419

8 0.0077748982 0.0010369512 15.3897201464

9 0.0072302833 0.0004923363 7.3069180831

10 0.0069594529 0.0002215059 3.2874385120

11 0.0068315063 0.0000935593 1.3885433338

12 0.0067748911 0.0000369441 0.5482991168

13 0.0067515774 0.0000136304 0.2022935634

14 0.0067426533 0.0000047063 0.0698477509

15 0.0067394718 0.0000015248 0.0226304878

16 0.0067384120 0.0000004650 0.0069013004

17 0.0067380809 0.0000001339 0.0019869438

18 0.0067379835 0.0000000365 0.0005416368

19 0.0067379564 0.0000000094 0.0001401700

20 0.0067379493 0.0000000023 0.0000345214

Along with the table of results, we obtain Figure 1.6.

Observe the dramatic decrease in the absolute error as the number of terms is

increased. The series converges much faster and accuracy improves with the addition

of each term. Only ten terms are required in the series to reach an accuracy of <5%.

For most applications, one may need to attain accuracies much less than 5%.

1.6.3 Finite difference formulas for numerical differentiation

In this section, the Taylor series is used to obtain the truncation errors

associated with ﬁnite difference formulas used to approximate ﬁrst-order

Figure 1.6

Rapidly decreasing error with increase in number of terms in the negative exponential series for x = 5 when using

a more efficient algorithm.

0 5 10 15 20

0.2

0.4

0.6

0.8

Number of terms in e

−x

series

Absolute error

Truncation error changes with number

of terms, x = 5

1.6 Taylor series and truncation error

Box 1.1B Oxygen transport in skeletal muscle

Earlier we determined the concentration profile of O

in the muscle tissue as

N ¼ N



LxðÞþ

4 Γ

 Γ

ðÞL

n¼∞

n¼1; n is odd

nπðÞ

 nπðÞ

Dt=L

sin

nπx



: (1:18)

The third term on the right-hand side of Equation 1.18 contains an infinite series called the Fourier

sine series. This particular sine series is a summation of only the terms with odd n. The terms

corresponding to even numbers of n are all identically zero. Therefore the first term in the Fourier series

expansion corresponds to n = 1, the second term corresponds to n = 3, and so on.

The diffusivity of O

in skeletal muscle is 1.5 × 10

–5

/s (Fletcher, 1980). The partial pressure of

in arterial blood is 95 mm Hg and in venous blood is 40 mm Hg. We assume an average O

partial

pressure of 66 mm Hg in the capillaries surrounding the muscle tissue. The solubility of O

in skeletal

muscle is 1.323 μM/mm Hg (Fletcher, 1980), from which we obtain the O

concentration N

at x =0,L

as 87 μM. The resting volumetric O

consumption in tissue Γ

is 50 μM/s, while, after heavy exercise,

volumetric O

consumption in tissue Γ

is 260 μM/s (Liguzinski and Korzeniewski, 2006). The distance

between two capillaries is L =60μm.

The oxygen concentration will be least in the region of the tissue that is farthest from the O

supply

zone, i.e. at x = L/2. We are interested in determining the change in O

concentration at x = L/2 with

time. The time taken for the first exponential term in the series e

 nπðÞ

Dt=L

to decay to e

1

is called the

diffusion time, i.e. t

¼ L

=π

D. It is the time within which appreciable diffusion has taken place. Note

that when the first exponential term in the series has decayed to e

1

, the second exponential term has

decayed to e

9

. After the diffusion time has passed, only the first term is important. In this example, the

diffusion time t

= 0.243 s.

Plotted in Figure 1.7 is the initial time-dependent O

concentration profile at x = L/2, after a sudden

jump in O

demand in the muscle tissue from 50 μM/s to 260 μM/s. In Figure 1.7(a), N at x = L/2

remains greater than zero up to a period t = 1 s. At the new steady state corresponding to conditions of

heavy exerise, N

=9μMatx = L/2. We can say that the entire tissue remains well oxygenated even at

times of strenuous exercise. Note that, for all t, the series converges quickly. Figure 1.7(b) is a close-up

Figure 1.7

Time-dependent oxygen concentration profile at the center of a slab of muscle tissue observed when the muscle

tissue enters from rest into a state of heavy exercise for (a) initial time elapsed of 0 to 1 s and (b) initial time

elapsed of 0 to 0.1 s.

0 0.5 1

t (s)

N at x = L/2 (μM)

n = 1

n = 3

n = 5

n = 7

0 0.05 0.1

t (s)

(a) (b)

n = 1

n = 3

n = 5

n = 7

Types and sources of numerical error

derivatives. The ﬁ rst-orde r derivative of a function f(x) that is differentiable at

x = x

is deﬁned as

ðxÞ¼lim

x!x

fxðÞfðx

x  x

If x is very close to x

, then the derivative of f with respect to x at x

can be

approximated as

ðÞﬃ

þ hðÞfðx

; (1:19)

where h = x – x

is small. Equation (1.19) can also be derived from the Taylor series,

with the advantage that we also get an estimate of the truncation error involved.

Rearranging the Taylor seri es formula given in Equation (1.12) we get

ðÞ¼

þ hðÞfðx



ðÞh



000

ðÞh

þ

look at the O

concentration at x = L/2 for the first 0.1 s after the sudden increase in O

demand, and

highlights the truncation errors involved as more terms are progressively retained in the Fourier series.

At t = 0.01 s, when only the first two terms are retained in the Fourier series, N(n = [1,

3]) = 69.7363. When the first three terms in the Fourier series are included then N(n = [1, 3, 5]) =

69.9224, which exhibits a relative difference of only 0.27%. Mathematically, we write

n¼5

 N

n¼3

 0:0027:

For all practical purposes (see Figure 1.8), only the first two terms must be retained in the series for

t ≥ 0.01 s to obtain a reliable estimate. The efficient convergence is due to the 1= nπðÞ

term in the

series that forces the rapid decay of higher-order terms. When t

, all terms in the Fourier series

summation except for the first term can be neglected. The MATLAB code used to generate Figures 1.7

and 1.8 is available on the Cambridge University Press website.

Figure 1.8

Estimated oxygen concentration N obtained by retaining n terms in the Fourier series. Estimates of N are plotted for

odd n, since the terms corresponding to even n are equal to zero.

0 5 10 15

60.5

61.5

62.5

Number of terms, n

N (μM) (x = L/2, t = 0.05 s)

1.6 Taylor series and truncation error

ðÞ¼

þ hðÞfðx



ξðÞh

; ξ 2 x

; x

þ h½

ðÞ¼

þ hðÞfðx

þ OhðÞ; (1:20)

with the truncation error of order h. The approximation given by Equation (1.20) for

a ﬁrst-order derivative can be rewritten as

ðÞﬃ

iþ1

ðÞfðx

; (1:21)

where h ¼ x

iþ1

 x

is called the ﬁrst forward ﬁnite difference, since each iteration

proceeds forward by using the value of fðxÞ from the current step i.

There are two other ﬁnite difference formulas that approximate the ﬁrst-

order derivative of a function: the backward ﬁnite difference and the central

ﬁnite difference methods. The backward ﬁnite difference formula is derived by

using the Taylor series to determine the function value at a previous step, as

shown below:

 hðÞ¼fx

ðÞf

ðÞh þ

ðÞh



000

ðÞh

þ (1:22)

i1

ðÞ¼fx

ðÞf

ðÞh þ

ðÞh

þ

ðÞ¼

ðÞfx

i1

ðÞ

ðÞh

2!h

þ;

from which we arrive at the formula for backward ﬁnite difference for a ﬁrst-order

derivative with an error of O(h):

ðÞﬃ

ðÞfx

i1

ðÞ

: (1:23)

To obtain the central ﬁnite difference equation for a ﬁrst-order derivative,

Equation (1.22) is subtracted from Equation (1.12), and upon rearranging the

terms it can be easily shown that

ðÞ¼

þ hðÞfx

 hðÞ

þ Oðh

ðÞﬃ

iþ1

ðÞfx

i1

ðÞ

: (1:24)

Note that the central forward difference formula has a smaller truncation error

than the forward and backward ﬁnite differences, and is theref ore a better approx-

imation method for a derivative. Box 1.6 addresses these three ﬁnite difference

approximation methods and compares them.

Types and sources of numerical error