Keyfitz N., Caswell H. Applied Mathematical Demography

Подождите немного. Документ загружается.

5.3. Mean Age in the Stable Population 105

Let us identify the terms of (5.3.3) for Irish males of 1968, using data

given in Keyﬁtz and Flieger (1971, p. 446). The cumulants of the life table

areasfollows:

=36.678

= 495.59

= 2243.9

= −240,862

r =0.01889.

Taking four terms in (5.3.3) approximates ¯x by

¯x ≈ 36.678 − 9.362 + 0.400 + 0.271 = 27.987.

This approximation to ¯x, the mean of the stable age distribution, 27.953,

is excellent. But Irish births have ﬂuctuated considerably, and the mean

of the observed age distribution is 31.806, about 4 years higher than the ¯x

calculated above.

For Colombia females of 1964 (Keyﬁtz and Flieger 1968, p. 191), the ﬁrst

approximation (5.3.2) to the mean ¯x of the stable age distribution is

¯x =

− σ

r =37.360 − (539.04)(0.0283)

=37.36 − 15.25 = 22.11.

In comparison, the stable age distribution shows a mean of 24.13 and the

observed female age distribution a mean of 22.32. More instances would

be needed to obtain a realistic estimate of the error of (5.3.2) as an ap-

proximation to the means of the stable and the observed age distributions,

respectively. Apparently the error increases with mortality and with r.

A growing population tends to be younger than the corresponding sta-

tionary population also within any particular interval of ages. An argument

identical to the one above may be applied to any age interval—we did not

require the limits to be 0 to ω in deriving ¯x ≈ (L

)−σ

r. Thus children

under 15 years of age are slightly younger, and people over 85 are younger,

in the growing than in the corresponding stationary population. With the

obvious redeﬁnition of its constants, (5.3.2) is not restricted to the whole

of life, but is applicable to any age interval.

Demographic Calculations Need Not Start at Age Zero. Various subgroups

can be deﬁned in such fashion that theory developed for whole populations

applies to them. We have already dropped down to one sex and refer to the

“female population,” a useful abstraction but an abstraction nonetheless,

since females cannot go through the process of birth and increase with-

out males. The “population over age 15” could similarly be described as

though it were self-contained. All of stable theory would apply with at most

an alteration in the deﬁnitions of symbols. Now “births” would be the in-

106 5. Fixed Regime of Mortality and Fertility

dividuals passing through their ﬁfteenth birthdays; survivorship would be

not l

, which we have been calling l

, but rather l

, x>15; the

stable fraction between x and x + dx would be



(x) dx = b



−rx

l(x)

dx,

where b



= l



−rx

l(x) dx, and evidently



(x) dx =

−rx

l(x) dx



−ra

l(a) da

By a further extension ages beyond 35, say, could be masked out and

an expression developed for the stable population aged 15 to 34 at last

birthday. It would similarly be feasible to recognize ages before birth, and

even, where data on fetal mortality are available, to go back to conception.

5.3.1 Use of Population Mean Age

Relationship (5.3.2) may be applied in the opposite direction—to tell the

rate of increase of a population when we know its mean age and the mean

and variance of the life table applicable to it. This way of estimating the

rate of increase of a population uses the data somewhat diﬀerently than

does (5.2.4).

Transposing (5.3.2) into the equivalent

r ≈

) − ¯x

(5.3.4)

provides an approximation to the rate of population increase r, given the

life table mean age L

, the variance of the life table age distribution

, and the observed mean age ¯x. Entering the ﬁgures for Colombia, 1964,

already used, we ﬁnd that

r ≈

) − ¯x

37.36 − 22.32

539.04

=0.0279,

as against the observed r =0.0283.

When the additional parameters κ

(skewness) and κ

(kurtosis) are

reliably enough available to be taken into account in estimating r,wecan

transform (5.3.3) into

∗

) − ¯x

− (κ

r/2) + (κ

/6)

. (5.3.5)

In this iterative form we would start with an arbitrary r on the right-

hand side, obtain the improved r

∗

, enter it on the right-hand side, obtain a

further improvement, and so continue. The iteration is a way of solving the

cubic equation in the unknown r represented by truncation of (5.3.3) after

5.4. Rate of Increase from the Fraction Under 25 107

the term in r

. Three or four cycles of iteration suﬃce for convergence to

considerably more decimal places than are demographically meaningful.

Note that the method requires, not complete knowledge of the life ta-

ble number-living column, but only its mean and other cumulants. In the

absence of a life table we would guess the L

and σ

of (5.3.4), per-

haps calculating them from a set of model tables. The less dependent the

outcome on the life table chosen, the more useful is the method. We are

encouraged to ﬁnd that the mean ages of the life table l(x)varyonlyabout

one-ﬁfth as much as their

, the expectation of life at age zero. For in-

stance, the Coale and Demeny (1966, p. 54) model West table for females

with

=55showsameanL

of 34.95, and that with

=60has

=35.96.

Countries and regions lacking birth data are likely to have inaccurate

censuses, and we want to rely on censuses only at their strongest points.

The art of this work is to take account of what ages are well enumerated and

what ones poorly enumerated, as well as to use the model with the weakest

assumptions. Literally thousands of ways of using the age distribution may

be devised, and ideally one should choose the method least sensitive to

(a) the accuracy of enumeration of ages; (b) the appropriateness of the

life table, which often has to be selected arbitrarily; (c) the assumption of

stability; and (d) possible in- and out-migration. To be able to choose from

among a large stock of methods is an advantage in many instances, and

the following sections continue our partial inventory of this stock.

5.4 Rate of Increase Estimated from the Fraction

Under Age 25

Suppose that a population is underenumerated at ages 0 to 4 because in-

fants are omitted, at 10 to 14 because some children of this age are entered

as 5 to 9, and at 15 to 19 because young adults are mobile and the enu-

merator sometimes fails to ﬁnd them. Suppose correspondingly that the

numbers 5 to 9 and 20 to 24 are overstated (Coale and Demeny, 1967,

p. 17), and that these errors oﬀset to some degree those mentioned in the

preceding sentence, so that the proportion under age 25, say α,isgiven

correctly. We would like to use nothing but α from a census, along with a

suitable life table, to estimate the rate of increase r.

Referring to the same stable age distribution (5.1.1), we can construct

an equation in which both the observed α and the unknown r appear.

The proportion of the population under age 25 is



−ra

l(a) da,where



−ra

l(a) da = 1. The ratio of the ﬁrst of these integrals to the second

108 5. Fixed Regime of Mortality and Fertility

canbeequatedtoα and the birth rate b canceled out:

α =



−ra

l(a) da



−ra

l(a) da

. (5.4.1)

The problem now is to solve (5.4.1) for the unknown r, supposing the life

table to be given.

One method is to leaf through a collection of model tables (e.g., Coale

and Demeny 1966) designed for such purposes, and ﬁnd among those for

the given mortality the one with an α that matches the given α.Ther of

that stable population is the solution to (5.4.1).

An alternative is an iterative formula to solve (5.4.1) for r,givenl(a):

multiply the numerator and denominator of the expression on the right-

hand side of (5.4.1) by e

10r

, then multiply both sides of (5.4.1) by e

−10r

/α,

next take logarithms of the reciprocals of both sides, and ﬁnally divide by

10 to obtain

∗

log

⎡

⎢

⎣



−r(a−20)

l(a) da



−r(a−10)

l(a) da

⎤

⎥

⎦

(5.4.2)

(Keyﬁtz and Flieger 1971, p. 28). This equation is algebraically identical to

(5.4.1) except that the r on the left has been starred to suggest its use in

iteration. Starting with an arbitrary r on the right, calculating r

∗

,entering

this on the right in place of r, and repeating, is a process that ultimately

converges to r

∗

= r, and whatever r satisﬁes this is also bound to satisfy

(5.4.1). The multiplication of (5.4.1) by e

−10r

/α (rather than e

−15r

/α,say)

is arbitrary, and experiment shows that e

−10r

provides fast convergence.

[Use the theory of functional iteration (e.g., Scarborough, 1958, p. 209) to

ﬁnd the optimum multiplier in place of e

−10r

/α.] This is an example of

how knowledge of the approximate magnitude of the quantities concerned

enables demographers to devise iterative procedures that are simpler than

more general ones such as the Newton–Raphson method.

To apply (5.4.2) we replace the integrals by ﬁnite expressions. The usual

rough but serviceable approximation is in 5-year intervals. For example, the

interval from a =0toa = 5 contributes to the integral in the numerator

of the logarithm in (5.4.2) the amount



−r(a−20)

l(a) da ≈ e

−r(2.5−20)

= e

17.5r

5.5. Birth Rate and Rate of Increase Estimated for a Stable Population 109

and similarly for the other 5-year age intervals. Then the iterative formula

becomes

∗

log

αΣ

ω−5

i=0

−r(i−17.5)

i=0

−r(i−7.5)

(5.4.3)

in terms of the

tabulated in published life tables (except that most life

tables are on radix l

= 100,000; that is, in terms of the symbols here used

they tabulate 10

). Summations in (5.4.3) are over i’s that are multiples

of 5. With zero as the arbitrary initial value of r, (5.4.3) converges to six

decimal places in from 3 to 10 cycles in most instances.

Method (5.4.3) is easily adapted to a split in the distribution at an age

other than 25, and it can be generalized beyond this to other fractions,

for example, the fraction of the population between ages 10 and 30, as

indicated by examples in Section 5.6.

5.5 Birth Rate as Well as Rate of Increase

Estimated for a Stable Population

We saw in (5.1.1) that in a closed population where birth and death rates

have been constant for a long time the proportion of individuals between

ages x and x+dx is c(x) dx = be

−rx

l(x) dx. Similarly the proportion of the

population between ages y and y +dy is c(y) dy = be

−ry

l(y) dy. To adapt to

5-year age intervals we integrated each equation over 5 years to construct

= be

−r(x+2.5)

= be

−r(y+2.5)

(5.5.1)

Dividing and taking logarithms, we obtained in Section 5.1

r =

y − x

log





. (5.5.2)

Now we go on to ﬁnd the value of b by eliminating r from the pair (5.5.1):

b =





(y+2.5)/(y−x)





(x+2.5)/(y−x)

. (5.5.3)

We derived these formulae by deﬁning

as an integral over a range of

ages in the stable population; we would apply the formulae by entering for

the observed fraction, from a census or estimate, over that range.

110 5. Fixed Regime of Mortality and Fertility

An alternative form with 10-year intervals is

b =exp

⎡

⎢

⎣

log(

)

x +5

−

log(

)

y +5

x +5

−

y +5

⎤

⎥

⎦

Entering the numbers for Colombian females, 1965, in thousands, for ages

5 to 15 and 20 to 30 (Keyﬁtz and Flieger 1971, p. 366, reproduced in Table

5.6 below) gives

b =exp

⎧

⎪

⎨

⎪

⎩

log[(2575/9125)/8.753]

−

log[(1401/9125)/8.550]

−

⎫

⎪

⎬

⎪

⎭

=0.0476,

or 47.6 births per thousand population.

There is no need to conﬁne the calculation to two ages (Bourgeois-Pichat,

1958). Taking logarithms in (5.5.1) provides a linear equation in r and log b

for each age:

log b − (x +2

)r =log





. (5.5.4)

Again in application we replace the stable proportions

by the observed

proportions P . For Colombian females, 1965, the needed quantities in the

six age intervals in the range 0 to 29 are shown in Table 5.4. The least

square line relating x +2

and log(

)is

−3.126 − (x +2

)(0.0352) = log





and this identiﬁes log b with −3.126 and r with 0.0352; hence b is esti-

mated at exp(−3.126) = 0.0439, r at 0.0352, and d, the death rate, at the

diﬀerence, 0.0087.

The ages to be used are at our disposal; which should we choose? With

only two age intervals x and y, as in (5.5.2), if x and y are equal, neither

(5.5.2) nor (5.5.3) tells us anything, and if they are close to each other the

answers will be sensitive to random errors in the population count identiﬁed

with

and

. On the other hand, choosing x and y far apart increases

the risk of straddling a substantial change in the birth rates that determine

the cohort sizes, that is, a departure from stability. If the probability of a

change in birth rates between x and y years ago is proportional to y − x,

the length of the interval between them, then for given random errors in

ages there will be an optimum choice of the interval y − x, perhaps in the

neighborhood of 25 years.

Suppose a single change in birth rates in the past, at a known or sus-

pected date D years ago. Making both x and y less than D, or both x and

y greater than D, is clearly advisable. If both x and y are less than D,

5.6. Several Ways of Using the Age Distribution 111

Table 5.4. Data for estimating b and r for Colombia, females, 1965

Observed Life table

x +2

log





0.1718 4.54231 −3.275

0.1558 4.39360 −3.339

0.1263 4.35979 −3.542

0.1048 4.33516 −3.722

0.0841 4.29919 −3.934

0.0695 4.25043 −4.113

Source: Keyﬁtz and Flieger (1971, p. 366).

the more recent rate of increase will be estimated; if they are greater, the

earlier rate.

If nothing is known about shifts in the past birth rate, and we want an

average of all rates that have prevailed during the lifetimes of persons now

alive, we might calculate all possible values of r and average them. The

average would be best weighted, with a maximum weight for y − x =25

years or thereabouts, and with lower weights as we moved toward y −x =0

or y −x = 50. The population above 70 provides little information on rate

of increase. Beyond 70 ages are inaccurately reported; the life table is less

precisely known; the survivors have passed through a variety of mortality

conditions; and their number is often too small to disregard sampling error

as we have done throughout.

5.6 Comparison of the Several Ways of Using the

Age Distribution

To summarize and extend the methods described above, still supposing sta-

bility, we extract from an observed age distribution the quantity

that is, the ratio of the observed persons x to x + m years of age to those y

to y+n. This ratio may be equated to the corresponding quantity estimated

from a life table and the rate of increase, which is approximately

−(x+m/2)r

−(y+n/2)r

and the equation provides the value for r:

r =

y +(n/2) − x − (m/2)

log





. (5.6.1)

112 5. Fixed Regime of Mortality and Fertility

Table 5.5. Rate of natural increase as estimated from pairs of age ranges,

Colombia, males, 1965

∗

y to (y + n − 1)

x to All

(x + m − 1) ages 5–ω 10–ω 0–69 5–69 10–69

0–14 0.03547 0.03486 0.03567 0.03569 0.03502 0.03589

0–24 0.03286 0.03294 0.03434 0.03290 0.03298 0.03452

0–34 0.03256 0.03278 0.03450 0.03256 0.03281 0.03473

0–44 0.03236 0.03274 0.03482 0.03230 0.03278 0.03512

5–19 0.03513 0.03439 0.03558 0.03548 0.03457 0.03587

5–29 0.03159 0.03231 0.03446 0.03135 0.03229 0.03472

5–39 0.03088 0.03245 0.03518 0.02939 0.03244 0.03563

5–49 0.03289 0.03318 0.03641 0.03270 0.03348 0.03723

∗

Programmed by Geoﬀrey McNicoll.

Where m and n are more than 5 years this approximation will not serve

and an iterative form is needed. Such a form was used to calculate the

entries in Table 5.5 (Keyﬁtz and Flieger 1971).

A special case is pairs of age intervals that approximately represent ratios

of female children to mothers, where now the y group is 30 years wide. In

Table 5.6,

gives r =0.03066. Again the estimates are mostly in

the range 3.0 to 3.5 percent, and all are greater than the 0.02814 provided

by registrations. The method has been named after William R. Thompson,

one of the pioneers of American demography.

Using age intervals x to x+4 and x+15 to x+44, so that the individuals in

the ﬁrst group are mostly the children of those in the second group, protects

in some degree against errors due to variation in the rate of increase of the

successive birth cohorts; that is, it protects against the inappropriateness

of the stability assumption. To see this we note that Thompson’s index,

Th =

x+15

, (5.6.2)

which is in this special case the contents of the square brackets in (5.6.1),

is an approximation to e

27.5r

. In fact r =(1/27.5) log Th is one way of

writing (5.6.1) for m =5,n = 30. In terms of the 5-year age groups of the

mother generation, (5.6.2) breaks down to

Th =

(

x+15

x+20

+ ···)

(

x+15

x+20

+ ···)

x+15

, (5.6.3)

where F

x+15

and so on are the age-speciﬁc rates of childbearing, in 5-

year intervals, counting for this purpose only children that live to the end

of the 5-year period. In eﬀect the N’s of (5.6.3) are weights on the F ’s.

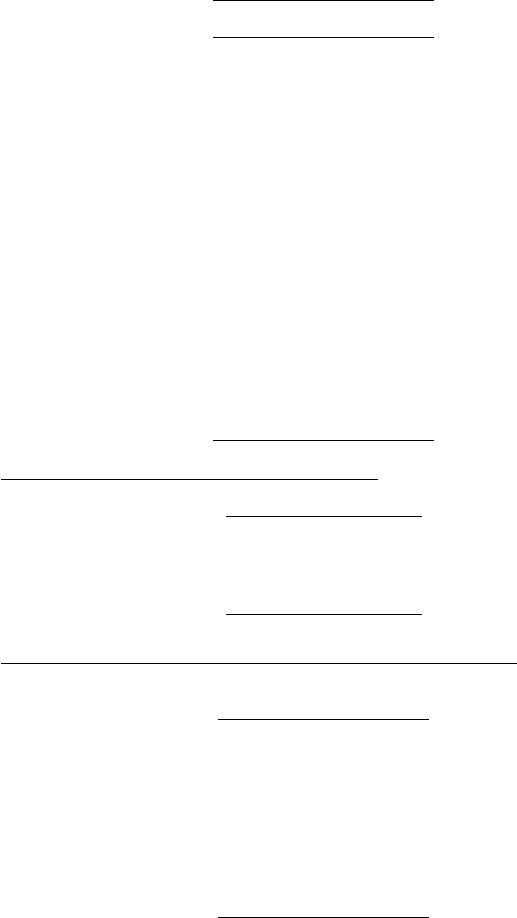
5.6. Several Ways of Using the Age Distribution 113

Table 5.6. Estimates of rates of increase for Colombia, 1965, females

∗

Part (a)

0 1,567,251 454,231

5 1,421,920 439,360

10 1,152,736 435,979

15 956,462 433,516

20 767,534 429,919

25 633,851 425,043

30 545,307 419,014

35 495,077 411,199

40 369,047 401,498

45 309,618 389,415

50 263,402 374,099

55 169,199 351,971

60 181,209 323,465

65 100,134 281,903

70 83,009 230,533

75 45,586 173,813

80 34,442 116,072

85+ 28,852 106,954

Total 9,124,636

1. Local stability (5.5.2) with 5-year age intervals

Age range r

5–9, 15–19 0.03831

10–14, 20–24 0.03927

15–19, 25–29 0.03917

20–24, 30–34 0.03161

2. Bourgeois-Pichat regression (5.5.4) based on 30-year age intervals

Age

range br

0–29 0.04388 0.03520

5–34 0.04616 0.03706

10–39 0.04210 0.03255

15–44 0.04153 0.03255

20–49 0.04024 0.03185

25–54 0.03973 0.03143

30–59 0.05287 0.03848

35–64 0.04377 0.03367

40–69 0.04636 0.03535

Table continues in part (b)

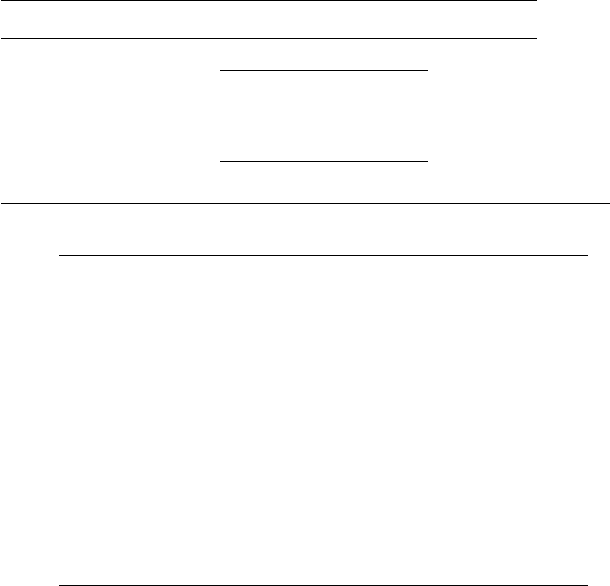
114 5. Fixed Regime of Mortality and Fertility

Table 5.6. (contd.) Estimates of rates of increase for Colombia, 1965, females

∗

Part (b)

3. Rate of increase from Thompson’s Index (5.6.2) by iterative method

Age range r

0–4, 15–44 0.03066

5–9, 20–49 0.03451

10–14, 25–54 0.03271

15–19, 30–59 0.03147

4. Rate of increase from pairs of wide age ranges using iterated version of (5.6.1)

Age All

range ages 5+ 10+ 0–69 5–69 10–69

0–14 0.03415 0.03345 0.03395 0.03430 0.03351 0.03407

0–24 0.03330 0.03269 0.03346 0.03340 0.03269 0.03356

0–34 0.03378 0.03281 0.03370 0.03403 0.03284 0.03385

0–44 0.03356 0.03243 0.03362 0.03392 0.03240 0.03378

5–19 0.03615 0.03441 0.03484 0.03675 0.03462 0.03508

5–29 0.03557 0.03347 0.03431 0.03662 0.03361 0.03455

5–39

†

0.03390 0.03480

†

0.03424 0.03521

5–49

†

0.03423 0.03524

†

0.03508 0.03587

10–24 0.03190 0.03157 0.03312 0.03163 0.03136 0.03323

10–34

†

0.03164 0.03382 0.03084 0.03125 0.03414

10–44 0.03385 0.02770 0.03353 0.03349 0.02204 0.03398

10–54 0.03438 0.04228 0.03237 0.03406 0.03873 0.03243

15–29 0.04068 0.02606 0.03105 0.03883 0.02327 0.03073

15–39 0.03504

†

0.03161 0.03461 0.03994 0.03116

15–49 0.03413 0.03719 0.02928 0.03393 0.03618 0.03561

15–59 0.03411 0.03613 0.03622 0.03395 0.03555 0.03454

∗

Programmed by Geoﬀrey McNicoll.

†

Indeterminate.

Source: Keyﬁtz and Flieger (1971, p. 366).

Under stability

x+20

will be e

−5r

(

x+20

x+15

) times as numerous as

x+15

; if it is not, the numerator and denominator of the top section of

(5.6.3) are aﬀected in the same direction.

In Table 5.6 the various methods described above are shown in appli-

cation to Colombian females. No single number is trustworthy, but the

collection shows a considerable degree of agreement, especially where wide

intervals are involved. The agreement with results for males as given in Ta-

ble 5.5 is also worth noting. [Show that (5.6.1) with the data in Table 5.6

gives 0.03042 for the ﬁrst entry under Thompson, and devise an iterative

form that will give the more accurate 0.03066.]

Fortunately these formulae are most applicable to populations of rapid

and fairly steady increase, which happen to be just the ones least pro-

vided with usable vital statistics, though they usually have recent censuses.