Кашкин В.Б., Сухинин А.И. Дистанционное зондирование Земли из космоса. Цифровая обработка изображений

Подождите немного. Документ загружается.

"(C,/X,„)

w(C

/X,„)

A D

, 4 V Условные плотности вероятности (разделение на два класса)

|КИ, для которых Х,„ > Х\ относятся к классу С

. Однако вероят-

jTb

того, что в первом случае точка может принадлежать к классу С

Цйчна

от нуля (область 1), как и то, что во втором случае точка X

при-

бежит к классу С| (область 2). Для класса С, область

является зо-

ложной тревоги (л.т), а область 2

—

зоной пропуска обнаружения

I).

Вероятности ложной тревоги Р

лт

и пропуска обнаружения Р

ио

рав-

соответственно площадям под областями

и 2 на рис. 4.6. Они оп-

рлиются соответственно выражениями

=lw(X

)

(

/»

Л1

(x„/q)rfx

Суммарная ошибка классификации равна сумме двух вероятностей:

р - р + р

•run ' л.т ' п. с

4.5. ПАРАМЕТРИЧЕСКИЕ МЕТОДЫ КЛАССИФИКАЦИИ

|,1.

Нормальный закон распределения

|дачах классификации

Изображение земной поверхности, полученное дистанционными

типами, представляет собой некоторое случайное поле. Яркость каж-

*h>

пиксела изображения складывается из яркостей природных объ-

171

ектов, попавших в мгновенное поле зрения сканера. Объекты по-р.>

ному, случайным образом, отражают и рассеивают солнечное излуч.

ние,

так что яркость каждого пиксела есть сумма случайных величин

Из теории вероятностей известно, что сумма независимых одинаков

распределенных случайных величин имеет нормальный (гауссовскпм

закон распределения при условии, что слагаемые вносят равномерно

м >

лый вклад в сумму (центральная предельная теорема). Существу!' •

обобщения центральной предельной теоремы на сумму зависимых с i

чайных величин, на сумму случайных величин с различными закон

ми распределения и т.п. Таким образом, есть основания полагать,

ч и

для природных объектов яркость пикселов подчиняется нормальном

закону распределения.

Названная причина не единственная, по которой в задачах парам

трического распознавания изображений широко используется гипоь

за о нормальном законе распределения яркости пикселов. При p.i>

познавании монохроматических изображений для распределспн••>

яркости почти всегда удается подобрать один из известных

одномер!

i ы •

законов (нормальный, биномиальный, экспоненциальный, пуасо.

новский и др.). Иное дело изображения, получаемые с помощью a i

неров, имеющих п>

спектральных каналов.

этом случае для опи» .•

ния статистических характеристик требуется «-мерное совмести'"

распределение яркости в каналах. Как указывают многие авторы, в

и•>

стоящее время уровень знаний таков, что пока точному многомерном

анализу, за редкими исключениями, поддаются лишь те задачи, i i

рассматривается нормальный многомерный закон распределения.

Существуют и чисто технические причины. Для записи в памп»

ЭВМ гистограммы, представляющей функции распределения верой

ностей яркости пикселов изображения, может потребоваться болып'>п

объем памяти. Число ячеек, необходимых для записи я-мерной гиси>

граммы, в которой каждое значение яркости может принимать

/г

урон

ней, равно

р".

Один из способов разрешения этой трудности

—

пред|

и •

ложить, что каждая гистограмма, или функция распределепп '

вероятностей, может быть адекватно аппроксимирована кривой, им'

юшей простую функциональную форму и зависящей от небольиии•

числа параметров.

частности, можно считать, что функция распре i

ления вероятностей для любого интересующего класса может бы и

представлена нормальной функцией.

Однако нормальная плотность вероятности предполагает, что ям

чения яркости могут быть отрицательными, хотя яркость всегда по i'

жительна; значения яркости в цифровом формате всегда ограничат

•

сверху. Нормальная ПЛОТНОСТЬ вероятности описывается одномодм

ной (имеющей один максимум) кривой. В то же время гистограмм

172

Представляющие функции распределения вероятностей яркости пик-

|||Лон изображения, могут быть многомодальными. Поэтому всегда

•дует помнить, что нормальная кривая дает приближенное описание

ймгности вероятности яркости изображения.

Для одномерного случая нормальная функция плотности вероятно-

нркости пикселов/, для некоторого класса к имеет вид

Щ(1и) =

л/2лс^

^хр|-(Л-Ц*)

/2о-2],

(/,./)

—

координаты пиксела; ц

.— математическое ожидание (сред-

!• шачение) яркости для класса к; а

<(f- И)

—

дисперсия ярко-

РИ

пикселов для класса к. Ниже используется также обозначение

На практике \i

и а

неизвестны и должны оцениваться по обуча-

ем выборкам. Несмещенные оценки для

и а

определяются вы-

дениями

Р*

~~^L,fm->

о;

/?,,

—г

'к -«II* -ТГтЁ^/т-Ц*)

(4.9)

(4.10)

—

общее число обучающих образов класса k,f

—

яркость пиксе-

I этого класса из /и-й обучающей выборки.

Предполагая, что функция вероятности любого класса может быть

||Нроксимирована нормальной функцией плотности, вместо всей ra-

il раммы в памяти ЭВМ можно хранить только математические ожи-

|Иия

дисперсии каждого класса

\х

и cs

. При двух спектральных ка-

Чйх двумерная функция распределения для каждого класса может

dlii оценена путем записи частот повторения всех возможных пар

Ичсиий яркостей одного и того же пиксела в двух каналах: каждая па-

достоит из значения/у, первого канала и значения/^

—

второго. Ре-

|M1i.TiiT будет представлять собой двумерную гистограмму. Но, как

одномерном случае, для экономии памяти ЭВМ можно предполо-

жи,

возможность параметрического представления функции распре-

лгння вероятностей нормальной функцией плотности вероятнос-

ти Двумерная нормальная функция плотности вероятностей имеет вид

173

(1у\,1ю) =

АехрВ

(/ffl-Mlt) , (Л^

^*)"

а?»

<£

'2 к

-2р

12*'

(Л'|-М1*)(Л-2-М2*)

~2 ^2

°1*°2*

(4.1

где

ЦЦ.

, \х

2к

22k

— математические ожидания или.

Персии яркости пиксела 1-го и 2-го каналов (для класса />

А =

(2ту

1к

2к

ф-р?,

Г\

B=-l2{\-p

)\->,p

2!k

[2k

/?i2*= Лги = <[(/*•! -Mi*)(/ff2-H2*)l> (4.1 •

—

коэффициент корреляции между яркостями пиксела в каждом кап

ле (для класса

Л).

На практике Л

неизвестен и должен оцениваться

м<

обучающим выборкам:

\2k -

\ Q

(4.

где/„,|

и/„

—значения яркости пикселов класса к из w-й обучают' ч

выборки.

Если параметры ц

, ц

2А

/?|

ц, Л

2*, Rm записаны в памяти ЭВМ л :

каждого класса (всего пять параметров для каждого класса), функции

распределения вероятностей для данных могут быть вычислены и"

формуле (4.11). Для ее упрощения можно использовать векторную

(MI

тричную) форму записи. Для общего случая п каналов обозначим во

тор данных (/, j )-го пиксела через

Ц,

вектор математического

ожида!

для к-го канала

—

через ц

, корреляционную матрицу

—

через R*:

iij\

fin

J ijn

м*

~V\k~

Vik

_n„k_

, R,=

^ II* R{\k R Wk ••• ^

II A

^Ш ^ lit ^11* ••• R\\k

R uk

II*

R\\k

(4.

«-мерную нормальную функцию плотности вероятностей

—

через

w„(f,j)

= (2я)-^| Rj-^expf-^-n^RrH^-u*)!, (4.

174

Шщв |Кд| — определитель ковариационной матрицы, R^

— обратная

Hi матрица, (fy—ц*)'

—

транспонированный вектор

(Ц—

\х

Таким образом, при справедливости параметрической гипотезы

Нормальном законе распределения яркости пикселов можно описы-

ь классы образов с помощью векторов математических ожиданий

корреляционных матриц. Опыт показывает, что методы классифика-

н, основанные на нормальном законе распределения, удовлетвори-

iflhiio работают даже при значительных отклонениях от нормальности.

Однако при использовании предположения о нормальности следу-

релить внимание двум вопросам. Во-первых, нужно подбиратьадек-

ные обучающие выборки, позволяющие оценивать математичес-

I ожидания и корреляционные матрицы каждого класса. Если при

'Нотификации используются данные п спектральных каналов, теоре-

Шски минимальное число обучающих образов (это могут быть оди-

ные пикселы) для каждого класса равно п + 1. При меньшем числе

чающих образов корреляционная матрица будет вырожденной (ее

рминант равен 0, и обратная матрица не существует), что делает не-

(Можным вычисление (4.15). На практике необходимо иметь Юл

iee обучающих образов, чтобы получить надежные оценки параме-

классов. Второй вопрос касается случаев, когда закон распределе-

Н явно многомодальный. Распространенное практическое реше-

—

представление многомодальной функции распределения в виде

мы нормальных законов.

^1.2.

Метод максимального правдоподобия

Пусть спутниковое сканерное изображение земной поверхности,

(ученное в п спектральных каналах, представляет собой совокуп-

|ТЬ пикселов, причем яркость

(/,у')-го

пиксела описывается вектором

[| п компонентами

—

значениями яркости в каждом канале. Требует-

| Отнести этот пиксел к одному из А'классов. Для этого предваритель-

к'очдается обучающая выборка

—

спутниковое изображение, на кото-

|М по наземным данным определены участки, отвечающие различным

16СНМ

(например, водоемы, сельхозпосевы, городские и сельские за-

ройки и т.п.). Пользователь указывает границы этих классов, проис-

|виг процесс обучения, т.е. компьютер оценивает вектор математиче-

|0п> ожидания и корреляционную матрицу для каждого из классов.

Далее производится обработка интересующего нас спутникового

йОражения. Для каждого пиксела компьютером определяется вектор

Юиврений fy

в каждом классе /сформируются условные плотности ве-

знптетей/?(f/,/Q). Для этого в многомерный нормальный закон рас-

ifWMr пения (4.15) вместо

Х,„

подставляется fy, а в качестве ц

и R

— за-

175

даваемые условия, т.е. упомянутые оценки вектора математически:

ожидания и корреляционной матрицы. Таким образом, для каждой-

пиксела формируется А"условных плотностей вероятностей, которые

сравниваются с некоторым порогом Q

согласно (4.7)-(4.8). Сравненп.

позволяет определить, какая из гипотез наиболее правдоподобна.

этом

и состоит метод максимального правдоподобия. Используя (4.15), im

лучаем, что отношение правдоподобия L

jxi\i\ классов к и /

l^l"'

/2ex

pHi/2)(f

-fT^'R^^ -m

P(lj/C

) |R

,/2

exp[-(l/2)(f

)

(f/

-fr/)]

Вместо отношения правдоподобия L

можно использовать любу

к-

монотонную функцию от него, например натуральный логарифм:

InL

=I|nj=4

i[(f

-\х

)

9Г

\Ц -р

)]-^«и "И/)'

/' ('*•-?/)]•

правой части в(4.7), (4.8) в этом случае будет стоять

\x\Q

Пер

вый член (l/^lnUR/l/lRj] и множитель 1/2 в выражении для \nL

MOI

быть включены в q

. Таким образом, задача выяснения, к какому клас

су относится (/,У)-й пиксел, сводится к сравнению квадратичных форм

щ-»

)

к-

\ц-Р*)]

кг„-р,у

{f„-pr,)].

Для простоты нередко полагают, что q

В этом случае считаем

ся,

что

(/,у')-й

пиксел относится к к-му классу, если для него эта квад

ратичная форма меньше, т.е. если компоненты вектора fy более тесно

группируются вокруг ц^..

Квадратичная форма [(fj/~P,t)

(fy-H*)] характеризует рассто

яние между объектом Ц и средним значением ц^ и часто применяется

в задачах распознавания изображений. Для вектора Ц, состоящего и i

двух компонентов, т.е. для двух спектральных каналов, квадратична-,!

форма имеет вид

k=-Z~=T

0-Р.2*)

3?.

\к

{fii\-V\k)

(fi

1-Vlk't

Р\2к

ZT~Ti

°7А°Ъ

(4.16

176

^ Распознавание методом максимального правдоподобия (МП) учи-

giyi«u"

достаточно большой объем статистических данных и позволя-

усмешно решать сложные задачи. При справедливости предполо-

МИН о нормальном законе распределения вектора f,-,- метод МП

спсчивает оптимальное распознавание. Однако, как можно заклю-

1й и

сказанного, этот метод требует достаточно большого числа опе-

;UHil и является сравнительно медленным. При его использовании для

рнПогки изображений желательно учитывать

спектральных каналах

Iни

I.KO

яркости каждого одиночного пиксела (пониксельная класси-

Киция), но и его окружение. К сожалению, такой учет приводит

ще большему замедлению процесса распознавания и на практике по-

ирименяется редко. Поэтому в некоторых случаях рассматривае-

|Й иариант метода МП проигрывает в качестве распознавания более

тым методам, которые принимают во внимание взаимные связи со-

МИХ

пикселов. Причиной неверной классификации могут быть гак-

Ш»ышенные значения

R„

Результат попиксельной классификации выгоревших участков ле-

(исходное изображение на рис. 4.2) методом МП можно видеть на

6.4.6. При обработке изображения использовалась обучающая выбор-

классов, как в методе ISODATA. Результаты классификации не-

1Л|.ко хуже, чем в методах ISODATA и сегментации путем наращива-

областей.

•-!»

•

iji.

"$».

к%б

<•-.

^Sfiis-v

••д*-'-'^.^

•

?. *:;:•

Рис 4.6. Рсчульт

спфикацин но

максимальною

п сноб

Hil-

ar клас-

мстолу

иравдо-

177

4.6.

ПРОСТЫЕ МЕТОДЫ, ОСНОВАННЫЕ НА ГРУППИРОВАНИИ

Квадратичную форму [(fy-jl*)

(f^-jl^)] можно упростить, ес-

ли положить

mpk

О,

т^р,

т.е.

не

учитывать корреляцию яркостен

пиксела в спектральных каналах. При этом в (4.16) все коэффициенты

Pi2/t=0,

к-

2,...,

п.

квадратичной форме (4.16) останутся только дв.:

члена, множитель перед квадратными скобками обратится в 1.

общем

случае получаем выражение

~ Li

Wijm ~fimk

1&~тк >

(4.17)

m=\

где

— номер спектрального канала,

— общее число каналов

При этом считается, что пиксел относится к тому классу, для которо!

< >

меньше значение г

. Однако точность определения

существенно

зависит от точности оценивания

тк

как и при методе МП. Дальней

шее упрощение приводит

методу минимальных расстояний (мини

мальных дистанций), когда решение

том,

какому классу относите:i

пиксел, принимается на основании сравнения расстояний между пик

селами и средними значениями в пространстве яркостей:

1к=Ъ(/цт-Ртк?-

(4. IX)

Этот самый простой и быстрый метод классификации требует ми

нимальных сведений о классах, но уступает методу МП в точности. Он

не учитывает окружения пиксела, поэтому, как правило, уступает и ме

тодам кластерного анализа, и методам сегментации по наращиванию об

ластей и выделению границ. Метод минимальных расстояний основа:

на евклидовой метрике

может рассматриваться безотносительно

к нормальному закону распределения.

Результат классификации методом минимальных расстояний мож

но видеть на рис. 4.7. Использовалась та же обучающая выборка, что

и в методах МП и ISODATA. Метод минимальных расстояний легко вы

деляет свежие, но пропускает старые пожарища, не относя к этим клас-

сам другие объекты.

На практике применяют еще один простой метод классификации,

связанный с нормальным законом,

—

метод параллелепипедов, назыв;:

емый иногда методом

прямоугольников.

Он использует сведения

клас

сах в виде векторов средних значений яркости ц

.и векторов дисперст

178

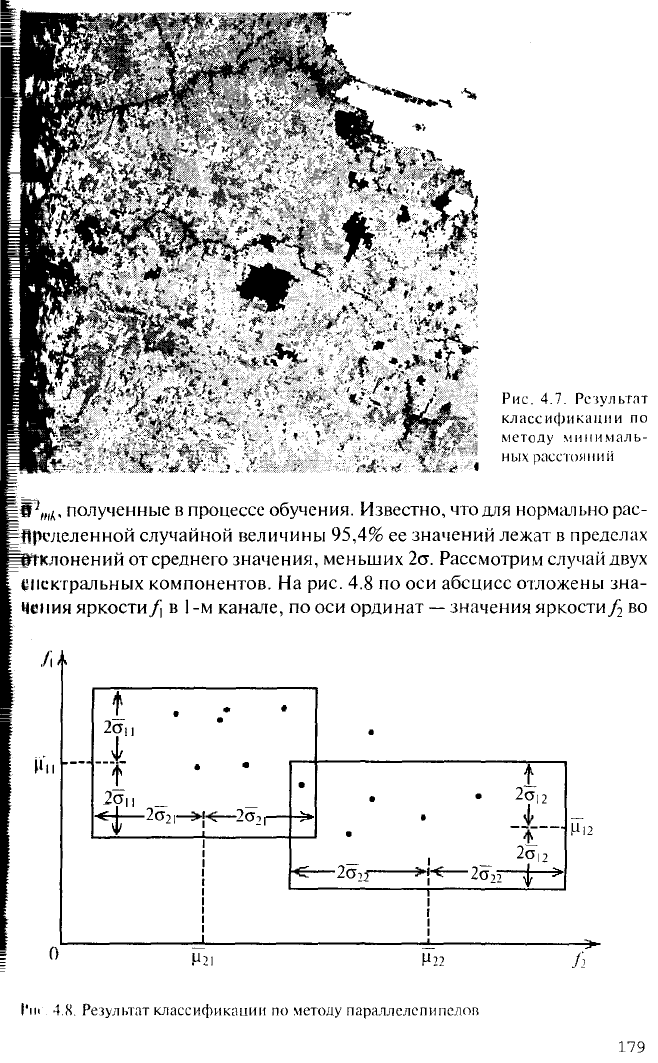
Рис.

4.7. Результат

классификации по

метолу минималь-

ных расстояний

,,^,

полученные в процессе обучения. Известно, что для нормально рас-

пределенной случайной величины 95,4% ее значений лежат в пределах

Втклонений от среднего значения, меньших 2о\ Рассмотрим случай двух

спектральных компонентов. На рис. 4.8 по оси абсцисс отложены зна-

мения яркости f\ в 1-м канале, по оси ординат

—

значения яркости^ во

/i*

Ми

2оц

<—2сь

^—2о

2Г

20]2

20|

->И—

2а

j )

Й12

M2I М22

I'm 4.К. Результат классификации по методу параллелепипедов

179

2-м канале. Здесь

же

указаны средние значения яркости uft

ц^

для

пер

вого и второго классов в

-м канале, цй и ujg для первого и второго

классов во 2-м канале. От значения средней яркости

обе стороны от

ложены значения среднеквадратического отклонения

afc,

ofo,

o"£,

a& для

первого

второго классов

каждом из каналов.

двумерном случае по

лучились прямоугольники, в трехмерном и более

—

параллелепипеды

в соответствующем пространстве. Если компоненты вектора яркости

fij\

/</2

попадают

в левый

прямоугольник, принимается решение о при

надлежности пиксела

первому

классу,

если они попадают

правый пря

моугольник

—

то ко

второму.

Прямоугольники

могут частично

перекры

ваться, что особенно характерно для областей, примыкающих к углам

этом случае возникает неопределенность.

Метод параллелепипедов относится к числу быстрых методов клас

сификации, однако по качеству распознавания уступает большинству

из рассмотренных. Его целесообразнее всего использовать

для

предва

рительной классификации. Он наиболее эффективен при нормальном

законе, так как для него выполняется упомянутое

«правило двух

сигма»

4.7.

НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ КЛАССИФИКАЦИИ

Задача непараметрической классификации возникает, когда вил

функций распределения

w„(fjj)

для совокупности классов неизвестен

Она состоит

том,

чтобы по классифицированным обучающим выбор

кам

{fy}

оценить плотности распределений ve„(fy)

и/или

сделать необхо

димые выводы о принадлежности вектора f^

тому или

иному

классу.

Ап

риорная информация, используемая при синтезе непараметрически\

систем классификации, скорее носит качественный характер, чем ко

личественный.

непараметрических методах главный

упор

делается не

на оптимизацию процесса классификации, а на обеспечение нечувст

вительности к условиям функционирования. Синтез непараметричес

ких классификаторов проводится преимущественно эвристическими

методами.

настоящее время при непараметрической классификации изоб

ражений

основном используют метод многомерных гистограмм, ме

тод Парзена, метод разложений по базисным функциям, метод поли

гонов Смирнова, различные методы локального оценивания, а также

некоторые методы нелинейного оценивания. Остановимся на методе

многомерных гистограмм.

При пороговой сегментации (см. рис. 4.1) было использовано свой

ство одномерной гистограммы (см. рис. 3.7) иметь моду (максимум)

180