Калинин Н.А., Толмачёва Н.И. Космические методы исследований в метеорологии

Тем самым оказалось возможным определять массы далеких не-

бесных тел.

32

Глава 2

ОСНОВЫ ТЕОРИИ ДВИЖЕНИЯ ИСКУССТВЕННОГО

СПУТНИКА ЗЕМЛИ

2.1. НЕВОЗМУЩЕННОЕ ДВИЖЕНИЕ

На движение искусственных спутников кроме гравитационной

силы оказывает влияние нецентральность поля земного тяготения, со-

противление атмосферы, притяжение других небесных тел, воздейст-

вие магнитных и электрических полей в космосе, давление солнечного

света и другие факторы, что затрудняет изучение закономерностей

этого движения.

Достаточно полное представление о законах движения ИСЗ

можно получить, если пренебречь многими из этих факторов и рас-

сматривать невозмущенное движение спутника, которое происходит

под действием притяжения только центрального тела — Земли.

2.1.1. Траектория полета. Уравнение движение спутника

Путь, описываемый спутником в пространстве вокруг централь-

ного притягивающего тела, называется траекторией, или орбитой.

Y

X

c

а

в

В

1

ϕ

r

2

А

0

А

1

F

1

П

В

директриса

ди

р

ект

р

иса

Земля

S

r

1

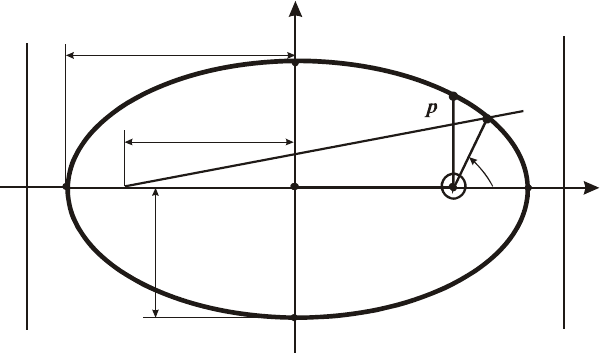
Рис. 2.1. Эллиптическая орбита спутника

33

В соответствии с первым законом Кеплера при невозмущенном

движении орбита движущегося небесного тела есть кривая второго

порядка, в одном из фокусов которой находится центр силы притяже-

ния, т. е. некоторое коническое сечение (гипербола, парабола, эллипс,

окружность или отрезок прямой). В качестве первого приближения

при изучении движения естественных и искусственных небесных тел

обычно используется эллиптическая орбита (рис. 2.1). В этом случае

траектория одного тела относительно другого является эллипсом, а

сами тела рассматриваются как некоторые материальные точки, что

справедливо только для тел сферической структуры, когда расстояние

между телами весьма велико по сравнению с их размерами.

Точки пересечения эллипса с осями координат А

1

(–а, 0), П (а,

0), B

1

(–b, 0), B(b, 0) называются вершинами эллипса (рис. 2.1). Рас-

стояния 2a и 2b между вершинами, а также отрезки, заключенные ме-

жду ними, называются соответственно большой и малой осями эллип-

са. Большая полуось а эллипса характеризует его геометрические раз-

меры. Ближайшая к притягивающему центру (Земля) точка П эллипти-

ческой орбиты спутника называется перигеем, а наиболее удаленная

точка А

1

— апогеем. Прямую, проходящую через апогей, центр Земли

и перигей, в астрономии называют линией апсид эллиптической орби-

ты ИСЗ. Для эллипса осями симметрии являются оси канонической

системы координат XOY, а начало координат — центром симметрии.

Точки F

1

(–c, 0) и А(с, 0) называются фокусами эллипса. Отношение

фокусного расстояния с к большой полуоси а, т. е.

a

c

=

ε

, (2.1)

называют эксцентриситетом. Эксцентриситет определяет форму ор-

биты спутника: она может быть эллипсом (

ε

< 1), окружностью (

ε

= 0),

параболой (

ε

= 1) или гиперболой (

ε

> 1). Прямые

ε

a

x ±=

(2.2)

называются директрисами эллипса, фокальными радиусами любой

точки S (положение спутника на орбите в какой-то момент времени)

называют отрезки прямых, соединяющих эту точку с фокусами F

1

и A.

Их длины r

1

и r

2

определяются соотношениями

r

1

= а +

ε

x и r

2

= а –

ε

x. (2.3)

Длину р отрезка AM, где A — один из фокусов эллипса, М —

точка пересечения перпендикуляра, восстановленного из фокуса к

большой оси, с эллипсом, причем справедлива формула

34

)1(

2

222

ε

−=

−

== a

a

ca

a

b

p

, (2.4)

называют фокальным параметром.

Уравнением движения спутника по эллиптической орбите мо-

жет служить уравнение эллипса в полярных координатах

ϑε

ε

ϑε

cos1

)1(

cos1

2

+

−

=

+

=

ap

r

, (2.5)

когда полюс полярной системы совпадает с одним из фокусов (в кото-

ром расположен центр притяжения), а полярная ось перпендикулярна

директрисе и направлена к ней из соответствующего фокуса (поляр-

ный угол в небесной механике принято обозначать

ϑ

). Однако это

уравнение не отражает динамики движения ИСЗ по орбите, так как

необходимо связать геометрическое положение спутника с текущим

временем.

Рассмотрим теперь общий случай невозмущенного движения

ИСЗ в центральном поле тяготения Земли. Размеры спутника малы по

сравнению с расстоянием его от земной поверхности (и тем более от

центра Земли). Допустим также, что вся масса Земли m

1

сосредоточена

в центре земного шара со сферическим распределением плотности, а

масса спутника т

2

сосредоточена в некоторой материальной точке. В

подобных случаях говорят, что масса тела сосредоточена в его бари-

центре (центре тяжести, центре масс).

Выберем в пространстве некоторую прямоугольную систему от-

счета XYZ, в которой вектор

α

= ОА определяет положение Земли А

(m

1

, x′, y′, z′), а вектор

ρ

= OS — положение спутника S (m

2

, x″, y″, z″);

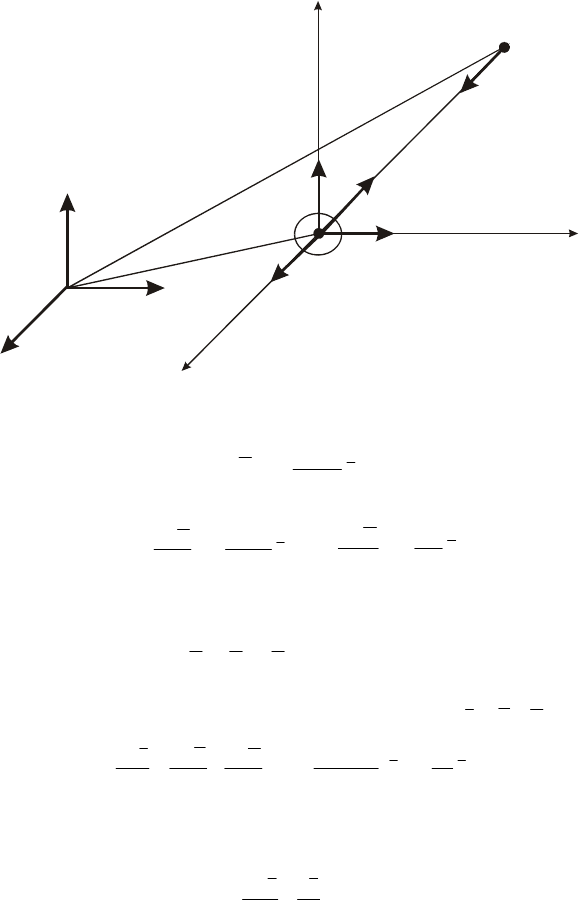
такая система представлена на рис. 2.2.

Вектор, у которого начало находится в притягивающем центре

Земли, а конец определяет положение спутника, называют радиус-

вектором ИСЗ (вектор r = AS).

По закону всемирного тяготения на спутник действует сила

притяжения Земли

r

mm

F

3

21

1

γ

−=

, (2.6)

т. е. можно записать, что

r

mm

d

t

d

m

3

21

2

γ

ρ

−=

, или

r

m

d

t

d

3

1

2

γ

ρ

−=

. (2.7)

Центр же Земли относительно системы XYZ испытывает воздей-

ствие со стороны спутника с силой

35

Z

Y

z

i

x

y

Земля

j

k

r

F

1

F

2

S

(x , y , z )

″

″″

0

ρ

Рис. 2.2. Положение спутника в пространстве

r

mm

F

3

21

2

γ

=

, (2.8)

т. е. можно записать, что

r

mm

dt

d

m

3

21

2

1

γ

α

=

, или

r

m

dt

d

3

2

γ

α

=

. (2.9)

В этих преобразованиях, согласно второму закону Ньютона, ле-

вая часть выражений (2.6) и (2.8) заменяется соотношением: сила =

масса тела × ускорение.

Конечно, силы

321

FFF ==

очень малы и ими можно было бы

пренебречь, но для характеристики движения важны не столько сами

силы, сколько вызываемые ими ускорения. Поскольку

α

ρ

−

=

r

, то

r

k

r

mm

dt

d

dt

d

dt

rd

33

21

2

−=

⎟

⎠

⎞

⎜

⎝

⎛

+

−=−=

γ

α

ρ

, (2.10)

где k =

γ

(m

1

+ m

2

) — гравитационная постоянная системы Земля –

ИСЗ.

Следовательно,

0

32

2

=+

r

rk

dt

rd

, (2.11)

36

есть уравнение движения спутника относительно притягивающего

центра Земли. Векторное уравнение (2.11) равносильно трем скаляр-

ным уравнения для декартовых координат спутника:

⎪

⎩

⎪

⎨

⎧

++===

′

−

′′

===

′

−

′′

=

′

−

′′

===

.;0

;;0

;;;0

22

32

2

32

2

32

2

zyxr

r

z

k

dt

zd

zzz

r

y

k

dt

yd

yyyxxx

r

x

k

dt

xd

(2.12)

Система уравнений (1.12) является исходной, для решения мно-

гих практических задач.

2.1.2. Плоскость орбиты спутника. Уравнение движения ИСЗ

в плоскости орбиты

Движение ИСЗ относительно Земли все время происходит в од-

ной и той же плоскости, проходящей через притягивающий центр.

Другими словами, радиус-вектор

r

спутника и его скорость

v

являют-

ся функциями времени, а их векторное произведение

cv

r

=

⋅

, (2.13)

где

c

— постоянный вектор. Умножая (1.13) почленно скалярно на r,

получим,

с ⋅ r = 0, (2.14)

т. е. радиус-вектор

r

спутника перпендикулярен вектору

c

, а это оз-

начает, что в любой момент времени он лежит в плоскости, пер-

пендикулярной вектору

c

и проходящей через центр Земли.

Плоскость, в которой движется спутник, называется орбиталь-

ной плоскостью.

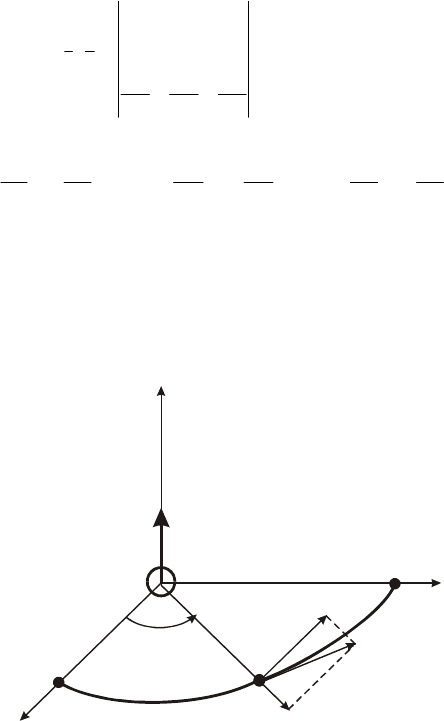
Действительно (рис. 2.3), если х", у", z" рассматривать как коор-

динаты точки S (положение спутника) в некоторой барицентрической

прямоугольной системе координат с началом в точке A (центре притя-

гивающей массы Земли), оси которой постоянно ориентированы в

пространстве, причем i, j, k — единичные векторы осей координат этой

системы, a c

1

, с

2

, c

3

— проекции вектора

c

на эти оси, то

r = x"i + y"j + z"k,

k

dt

zd

j

dt

yd

i

dt

xd

v

′

+

′

+

′

=

, (2.15)

с = с

1

i + c

2

j + c

3

k.

37

Поскольку

kcjcic

dt

zd

dt

yd

dt

xd

zyx

kji

vr

321

++=

′′′′′′

=⋅

, (2.16)

то

d

t

yd

z

d

t

zd

yc

′

′′

−

′′

=

1

;

d

t

zd

x

d

t

xd

zc

′′

−

′

′′

=

2

;

dt

xd

y

dt

yd

xc

′

′′

−

′

′′

=

3

. (2.17)

Теперь уравнение плоскости движения спутника (2.14) можно

записать в следующем виде:

с = с

1

x + c

2

y + c

3

z. (2.18)

К этому же выражению (2.18) орбитальной плоскости можно

прийти путем несложных преобразований и интегрирования системы

уравнений движения спутника (2.12), записанных в декартовых коор-

динатах.

X

Z

Y

А

З

емля

r

р

М

S

с

Vп

V

Vr

П

ϑ

Рис. 2.3. Орбитальная плоскость спутника

Поскольку движение ИСЗ происходит в орбитальной плоскости, про-

ходящей через барицентры Земли и спутника, систему координат в

дальнейшем целесообразно строить так, чтобы ее начало совпадало с

центром Земли, ось

z была перпендикулярна орбитальной плоскости, а

оси

х и у образовали правую систему координат (рис. 2.3). Тогда с

1

= с

2

= 0 и с = с

3

, т. е.

38

c

dt

dx

y

dt

dy

x =−

. (2.19)

Соотношение (2.19) есть уравнение движения ИСЗ в орби-

тальной плоскости (координата

z = 0). Заметим, что оси х и у в орби-

тальной плоскости могут быть ориентированы произвольно.

Для того чтобы при решении различных астрономических задач

суточное и годовое движение Земли вызывали бы наименьшие изме-

нения координат орбитальной плоскости

ИСЗ, координатную систему,

в которой определяется эта плоскость, обычно совмещают с экватори-

альной системой небесных координат с началом отсчета в точке ве-

сеннего равноденствия. Точки пересечения проекции орбиты ИСЗ с

экватором называют узлами:

восходящий узел, если спутник переходит

из южного полушария в северное, и

нисходящий узел, если спутник

переходит из северного полушария

в южное (соответственно точки M

и

L на рис. 2.4).

2.1.3. Элементы орбиты и параметры движения спутника

Элементы орбиты ИСЗ. В общем случае движение ИСЗ опи-

сывается тремя дифференциальными уравнениями (2.12) второго по-

рядка. Следовательно, порядок всей системы равен шести. Другими

словами, пространственные координаты спутника выражаются функ-

циями независимой переменной времени и некоторых произвольных

постоянных.

Параметры, позволяющие однозначно определить положение

спутника в пространстве в любой момент времени, называются

эле-

ментами орбиты спутника.

Элементы орбиты ИСЗ определяются (рис. 2.4):

– положением орбитальной плоскости в пространстве отно-

сительно выбранной системы координат, которое задается прямым

восхождением восходящего узла

Ω (т. е. углом между направлением в

точку весеннего равноденствия и линией узлов

ML) и наклонением

орбиты

i (т. е. углом между плоскостью экватора и плоскостью орби-

ты);

– положением орбиты в плоскости движения, которое характе-

ризуется либо склонением перигея

δ

п

, либо его угловым расстоянием

ω

(по проекции орбиты от восходящего узла до проекции перигея),

поскольку в сферической тригонометрии определена зависимость

sin

ω

= sin

δ

п

coseci; (2.20)

– формой (эксцентриситетом

ε

) и размерами (большой полу-

осью

а) орбиты;

39

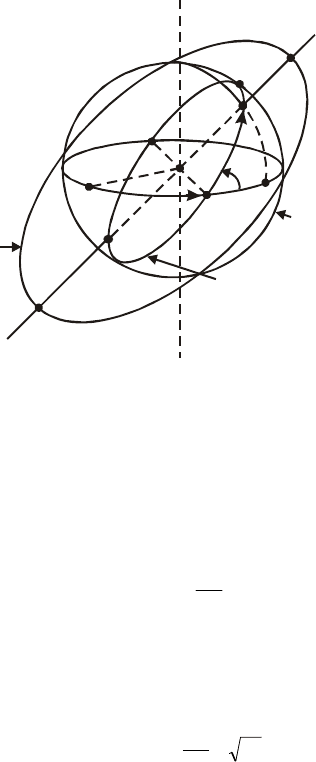
– моментом t

0

нахождения спутника в какой-либо точке орбиты

(например, в перигее).

Таким образом, положение ИСЗ в пространстве в любой момент

времени определяется заданием шести параметров—элементов орби-

ты:

Ω, i,

δ

п

или

ω

,

ε

, a, t

0

.

Р

N

Р

S

А

1

П

1

γ

Ω

ω

δ

ϕ

S

М

L

i

П

еригей

Апогей

Ось мира

Орбита

ИСЗ

Н

ебесная сфера

П

роекция орбиты ИСЗ

на небесную сферу

Рис. 2.4. Элементы орбиты спутника

Скорость движения и период обращения спутника на орби-

те.

Рассматривая выражение (2.19) в полярных координатах (рис. 2.3)

и принимая во внимание, что

x = rсоs

ϑ

и y = rsin

ϑ

, (2.21)

получим

c

dt

d

r =

ϑ

2

. (2.22)

Следовательно, чем дальше спутник от центра притяжения, тем мень-

ше его угловая скорость. Это согласуется со вторым законом Кеплера:

площадь, описываемая радиус-вектором спутника ( ), пропорцио-

нальна времени (

dt), в течение которого она описана:

ϑ

dr

2

kp

d

t

d

r =

ϑ

2

. (2.23)

40

Тогда скорость движения ИСЗ на эллиптической орбите можно пред-

ставить соотношением

⎟

⎠

⎞

⎜

⎝

⎛

−=

ar

kv

12

, (2.24)

из которого видно, что в различных точках орбиты скорость движения

спутника меняется: она максимальна в перигее и минимальна в апогее.

Это обстоятельство усложняет применение эллиптических ор-

бит для исследования Земли из космоса. Для этих целей удобнее ис-

пользовать частный случай движения ИСЗ по круговой орбите со ско-

ростью

const

r

k

v

кр

==

, (2.25)

так как при этом

r = a = const. У поверхности Земли (r ≈ 6370 км) v

кр

должна быть равной 7,91

км/с. Эту скорость чаще называют первой

космической скоростью

и обозначают v

I

. Однако из-за наличия атмо-

сферы и других причин круговая орбита вблизи земной поверхности

практически неосуществима.

Орбита, на которой спутник способен совершить хотя бы один

полный оборот, называется

стандартной. Высота стандартной орбиты

равна 160

км, но в теоретических расчетах ее округляют до 200 км. На

этой высоте круговая скорость (первая космическая скорость) состав-

ляет 7,79

км/с.

Заметим, что на земной поверхности проекция траектории ИСЗ,

движущегося по круговой орбите, проходящей через полюс Земли, не

совпадает с направлением меридиана, поскольку угловая скорость вра-

щения Земли вдоль меридиана изменяется. Максимальный угол откло-

нения этой проекции от меридиана наблюдается на экваторе и состав-

ляет 86°45

′ (угловая скорость вращения Земли здесь равна 450 м/с).

Еще более сложную кривую представляет аналогичная проекция, если

радиус орбиты увеличить до 42180

км. На такой орбите спутник со-

вершает полный оборот за одни звездные сутки.

Если эллиптическая орбита, вытягиваясь (

а

→

∞

), приближается

к прямой линии, то можно определить параболическую скорость уда-

ления спутника от Земли (ее иногда называют

скоростью освобожде-

ния

)

кркросв

vv

r

k

v 41,12

2

≈==

. (2.26)

41

Калинин Н.А., Толмачёва Н.И. Космические методы исследований в метеорологии

Подождите немного. Документ загружается.