Кадеев А.А. Домашняя работа по алгебре за 11 класс
Подождите немного. Документ загружается.

170
№ 1164
1) 3
2х
– 3
х
= 72, 3
2х
– 3
х
= 3
4
– 3
2
, 3
х
(3
х
– 1) = 3
2
(3
2
– 1), х = 2;
2) 4
х
– 2
х+1
= 48, 2
2х
– 2
х+1
= 48, 2
х
(2
х
– 2
1
) = 2
3
(2
3
– 2
1
), х = 3.
№ 1165
1) (log
2
x)
2
– 3log
2
x + 2 = 0.
Пусть log
2
x = a, тогда уравнение примет вид: а
2
– 3а + 2 = 0,
а
1
= 1, а
2
= 2, т.е. log
2
x = 1, x = 2, log
2
x = 2, x = 4.
Ответ: х = 2, х = 4
2) (log
3
x)
2
+ 5 = 2log
3
x
3
, (log
3
x)
2
+ 5 – 6log
3
x = 0, log
3
x = a,
a
2
+ 5 – 6a = 0, a
2
– 6a + 5 = 0, a
1
= 1, a
2
= 5, т.е. log
3
x = 1, x = 3,
log
3
x = 5, log
3
x = log
3
3
5
, x = 3
5
= 243
Ответ: х = 3, х = 243.
№ 1166
1)
()
2ln
1
2
ln +=
+
x
x
, ln2 – ln(x + 1) = ln(x + 2),
()
02ln
1
2
ln =+−
+
x
x
,
()( )
1ln
21
2
ln =
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++
xx
,
()( )
1
21
2
=
++
xx
, 2 = х2 + 3х + 2, х2 + 3х = 0,
х = 0, х = -3, при х = -3 ln(x + 2) не определен.
Ответ: х = 0
2)
13log63log
33
=−−− xx , 3log
3
63
log
33
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
x
x
,
3
3
63
=
−
+
x
x
,
3х – 6 = 3
2
(х – 3), 3х – 6 = 9х – 27, 21 = 6х, х = 3,5.
№ 1167
1)
xx lg
2
1
lg
2
1
lg −=
⎟
⎠
⎞
⎜
⎝
⎛
+
,
x
x
2
1
lg
2
1
lg =
⎟
⎠
⎞
⎜
⎝
⎛
+
,
1lg2
2
1
lg =
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+ xx ,
12
2
1
=
⎟
⎠
⎞
⎜
⎝
⎛
+ xx , х + 2х
2
= 1, 2х
2
– х – 1 = 0, х
1
= -1,
2
1
2
=x
,
при х = -1 lg x не определен.
Ответ:
2
1
=x
2)
2
6
1
lglg2
x
x
−
−=
, 0
6
1
lglg
2
2
=
−
+
x
x ,
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>−
>
=
−
−
06
0
1lg
6
lg
1
2
2
2
x
x
x
x
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>−
>
−=
−
−
06
0
6
6
1
2
2
2
2
x
x
x
x
x
()
⎪
⎩
⎪
⎨
⎧
>−
>
−=
−
06
0
6
1
2
22
x
x
xx
()
⎪
⎩
⎪
⎨
⎧
>−
>
±=
−
06
0
3
1
2
x
x
x
3=x .
171
№ 1168
1) log
2
(2x – 18) + log
2
(x – 9) = 5, log
2
(2x – 18)(x – 9) = log
2
2
5
,
()()
⎩
⎨
⎧
>−
=−−
0182
29182
5
x
xx
, 2х
2
– 18х – 18х + 162 – 32 = 0,
2х
2
– 36х + 130 = 0, х
2
– 18х + 65 = 0,
49
1
65819
2,1
±=
−±
=x ,
⎩
⎨
⎧
>
==
9
5 ,13
21
x
xx
. Ответ: х = 13
2) lg(x
2
+ 19) – lg(x + 1) = 1, lg((x
2
+ 19) : (x + 1)) = lg10,
⎪
⎩
⎪
⎨
⎧
>+
=
+
+
01
10
1
19
2
x
x
x
⎩
⎨
⎧
−>
+=+
1
101019
2
x
xx
⎩
⎨
⎧
−>
=+−
1
0910
2
x
xx
⎩
⎨
⎧
−>
==
1
9 ,1
21
x
xx
Ответ: х = 1, х = 9.
№ 1169
1) 05565
3
2
3
loglog
=+⋅−
xx
.
Пусть log3x = a, тогда уравнение примет вид: 5
2а
– 6 ⋅ 5
a
+ 5 = 0,
(5
a
)
2
– 6 ⋅ 5
a
+ 5 = 0, 5
a
= 1, a = 0 = log
3
x, x = 1, 5
a
= 5, a = 1 = log
3
x, x = 3.
Ответ: х = 1, х = 3.
2) 1255425
1loglog
33
=⋅−
+xx
,
(
)
1255545
33
log
2
log
=⋅⋅−
xx
.
Пусть
a
x
=
3
log
5, тогда уравнение примет вид: а
2
– 20а – 125 = 0,
1510
1
12510010
2
1
±=
+±
=a
, а
1
= 25, а = -5; а
2
не является решением,
т.к. 055
3
log
<−≠
x
,
2
log
55
3
=
x
, log
3
x=2, х=9. Ответ: х = 9.
№ 1170
1) x
lgx
= 10.
Прологарифмируем обе части уравнения по основанию х:
log
x
x
lgx
=log
x
10,
x
x
lg
1
lg = , lg
2
x=1, x=0, но x>0, следовательно, решений нет.
2) xx
x
9
3
log
= .
Прологарифмируем обе части уравнения по х:
xx
x
x
x
9loglog
3
log
= ,
log
3
x = log
x
x + log
x
9, log
3
x = 1 + 2log
x
3,
x
x
3
3
log
2
1log += ,
log
3
2
x–log
3
x–2=0, log
3
x=-1, x=3
-1
, log
3
x = 2, x = 9. Ответ:
,
3
1
=x
х = 9.
3) x
lgx
– 1 = 10(1 – x
-lgx
), x
lgx
– 1 = 10 – 10x-l
gx
, x
lgx
+ 10
-lgx
– 11 = 0.
Пусть lgx = y, тогда х = 10
у
и уравнение примет вид:
(10
у
)
у
+ 10 ⋅ (10
у
)
-у
– 11 = 0, 011
10
10
2
2
=−+
y
y
.
172
Пусть
z
y
=
2
10 , тогда уравнение примет вид:
011
10
=−+
z
z
, при z ≠ 0,
z
2
– 11z + 10 = 0, z
1
= 10, z
2
= 1, тогда
1010
2
=
y
, у = ± 1 и
110
2
=
y
, у = 0,
тогда х = 10
±1
, х = 10
0
(заметим, что x > 0). Ответ: х = 1, х = 10, х = 0,1.
4)
xx
xx = .
Заметим, что х = 1 – решение, далее
xx
xx =
⎟
⎠
⎞
⎜
⎝
⎛
2
;
xx
xx =
2
, пусть
yx = , х = у
2
, и уравнение примет вид:
(
)
(
)
2
22
2
y
y
yy = ; 2у = у
2
,
у
2
– 2у = 0, у(у – 2) = 0, у = 0, у = 2, тогда х = 0, х = 4, но 0
0
не определен.
Ответ: х = 1, х = 4.
№ 1171
1) 049214947
222
=⋅+⋅−⋅
xxx
, 07272927
22
2222
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅+⋅⋅−
⎟
⎠
⎞
⎜
⎝
⎛
⋅
xxxx
,
02
7
2
9
7
2
7
22
2
2
=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
xx
x
x
.
Пусть
a
x
=
⎟
⎠
⎞
⎜
⎝
⎛
2
7
2
, тогда уравнение примет вид: 7а
2
– 9а + 2 = 0
14
59
14
56819
2
1
±
=
−±
=
a
, а
1
= 1,
7
2
2
=a , тогда
а)
1
7
2
2
=
⎟
⎠
⎞
⎜
⎝
⎛
x
, т.е. х = 0; б)
7
2
7
2
2
=
⎟
⎠
⎞
⎜
⎝
⎛
x
, т.е. х = ±1. Ответ: х = 0, х = ±1.
2) 5
х+4
+ 3 ⋅ 4
х+3
= 4
х+4
+ 4 ⋅ 5
х+3
, 5
4
5
х
+ 3 ⋅ 4
3
⋅ 4
x
= 4
4
⋅ 4
x
+ 4 ⋅ 5
3
⋅ 5
x
,
625 ⋅ 5
x
+ 192 ⋅ 4
x
= 256 ⋅ 4
x
+ 5 ⋅ 100 ⋅ 5
x
,
5100
5
4
256
5
4
192625 ⋅+
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅+
xx
,
3
5
4
5
4
;125
5
4
64
−
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
xx
.
№ 1172
1)
(
)
132log
4
=++ x ,
(
)
4log32log
44
=++ x ,
⎩
⎨
⎧
≥+
=++
03
432
x
x
⎩
⎨
⎧
−≥
=+
3
43
x
x
, х = 1.
2)
2
1
2log
2
3
1
−=− xx ,
(
)
2
1
3
1
2
3
1
3
1
log2log
−
=− xx ,
()
⎪
⎩
⎪
⎨
⎧
>−
=−
02
32
2
2
2
xx
xx
()
⎩
⎨
⎧
>−
=−−
02
032
2
xx
xx
()
⎩
⎨
⎧
>−
=−=
02
3 ;1
21
xx
xx
х = -1, х = 3.
173
3)
()
2log24log1log
2
1
333
−+=+ xx
,
()
2log4log1log
33
2
1
3
−+=+ xx
,
()
2
4
log1log
3
2
1
3
+
=+
x
x
,
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>+
>+
+
=+
04
01
2
4
1
x
x
x
x
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−>
−>
+=+
4
1
1
4
1
x
x
x
x
⎩
⎨
⎧
−>
=−−+
1
0444
x
xx
⎩
⎨
⎧
−>
=
1
0
x
x
х = 0
№ 1173
1) х
1+lgx
= 10x,
Прологарифмируем по основанию х: log
x
x
1+lgx
= log
x
10x,
1 + lg x = 1 + log
x
10,
x
x
lg
1
1lg1 +=+ , lg
2
x = 1; lg x = ±1, x = 10, х = 0,1.
2) x
lgx
= 100x.
Прологарифмируем обе части уравнения по основанию х:
log
x
x
lgx
= log
x
100x, lg x = log
x
100 + 1, lg x = 2lg
x
10 + 1,
1
lg
2
lg +=
x
x , lg
2
x = 2 + lg x, lg
2
x – lg x – 2 = 0;
1) lg x = -1,
1,0
10
1
10
1
===
−
x
; 2) lg x = 2, x = 10
2
= 100.
3) log
2
(17 – 2
x
) + log
2
(2
x
+ 15) = 8,
()()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>+
>−
=+−
0152
0217
2log152217log
8
22
x
x
xx
, (17 – 2
x
)(2
x
+ 15) = 2
8
,
17 ⋅ 2
x
+ 17 ⋅ 15 – 2
2x
– 15 ⋅ 2
x
= 256, 2
2x
- 2⋅ 2
x
+ 1 = 0.
Пусть 2
х
= а, тогда уравнение примет вид:
а
2
– 2⋅а + 1 = 0, (а – 1)
2
= 0, а = 1, т.е. 2
х
= 1, х = 0,
⎪
⎩
⎪
⎨
⎧
>+
>−
=
0152
0217
0
x
x
x
х = 0.
4) log
2
(3 + 2
x
) + log
2
(5 – 2
x
) = 4,
()()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>−
>+
=−+
025
023
42523log
2
x
x
xx
, (3 + 2
x
)(5 – 2
x
) = 16, 15 – 3 ⋅ 2
x
+ 5 ⋅ 2
2x
= 16,
-2
2x
+2⋅2
x
–1=0, 2
2x
–2⋅2
x
+1=0; (2
x
–1)
2
, 2
x
= 1; x = 0;
⎪
⎩
⎪
⎨
⎧
>−
>+
=
025
023
0
x
x
x
х = 0.
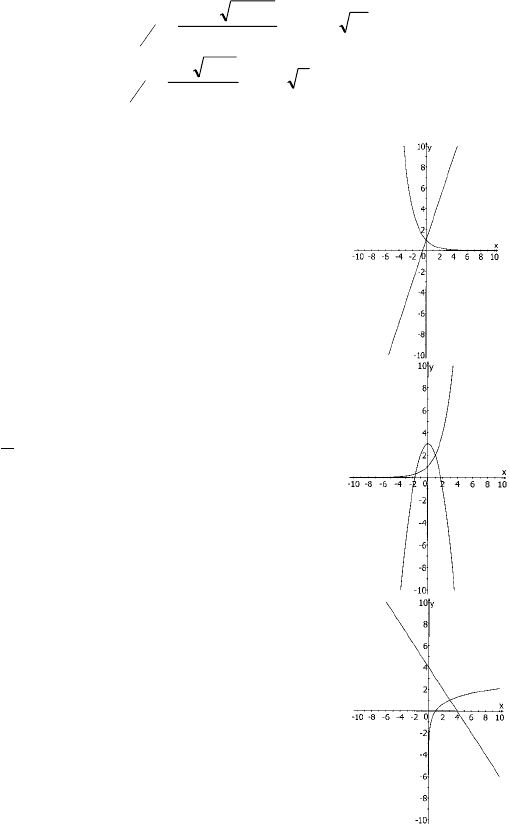
174
№ 1174
Ответ: не могут
m, n, k – действительные числа
x
2
– (m + n)x + mn – k
2
= 0; D=b
2
–4ac=(m+n)
2
–4(mn–k
2
)=m
2
+2mn+n
2
–
– 4mn – 4k
2
= m
2
+ n
2
– 2mn + 4k
2
= (m – n)
2
+ 4k
2
≥ 0.
№ 1175
1) z
2
+ 4z + 19 = 0, 152
1
1942
2
1
iz ±−=
−±−
= ;
2) z
2
– 2z + 3 = 0, 21
1
311
2
1
iz ±=
−±
= .
№ 1176
1) 0,5
х
= 2х + 1.
Построим графики функций
у = 0,5
х
и у = 2х + 1:
Очевидно, графики функций пересекаются
в точке (0,1), т.е. х = 0
2) 2
х
= 3 – х
2
Построим графики функций
у = 2
х
и у = 3 – х
2
:
8,1,
2
3
21
−≈≈ xx
3) log
3
x = 4 – x
Построим графики функций
y = log
3
x и y = 4 – x:
х = 3.
175
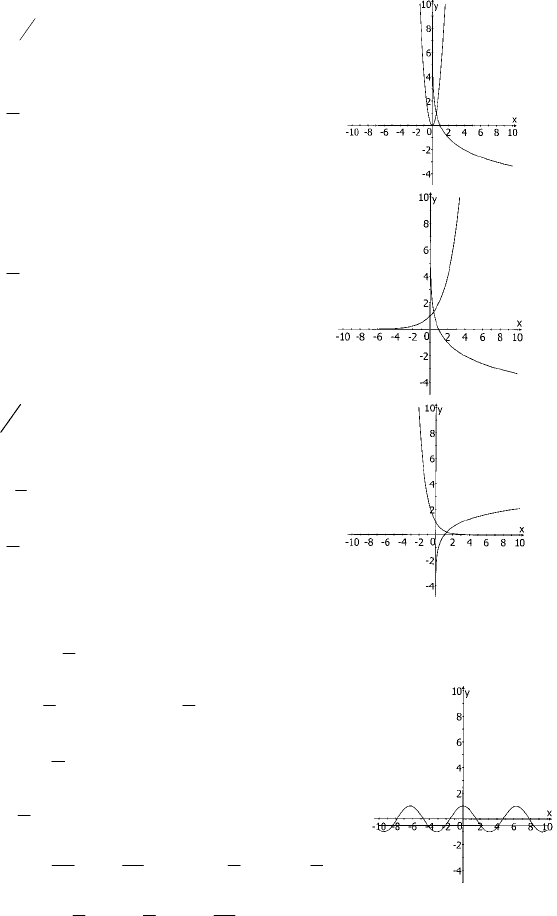
4)
2
2
1
4log xx =
Построим графики функций
у = log
½
x и у = 4х
2
2
1
=x
5) 2
х
= log
0,5
x
Построим графики функций
у = 2
х
, y = log
½
x
2
1
≈x
6)
()
x
x
3
log
3
1
=
Построим графики функций
x
y
⎟
⎠
⎞
⎜
⎝
⎛
=
3
1
и y = log
3
x
2
3
≈x
№ 1177
1)
2
1
cos −=x
[-π; 3π]
2
1
cos −=x
, Znnx ∈π+
⎟
⎠
⎞
⎜
⎝
⎛
−±= ,2
2
1
arccos
Znnx ∈π+
⎟
⎠
⎞
⎜
⎝
⎛
π
−π±= ,2
3
,
Znnx ∈π+π±= ,2
3
2
,
n = 1,
3
8
,
3
4 π
=
π
= xx
, n=0,
π−=π=
3
2
,
3
2
xx
Ответ:
3
8
,
3
4
,
3
2 π
=π=π±= xxx
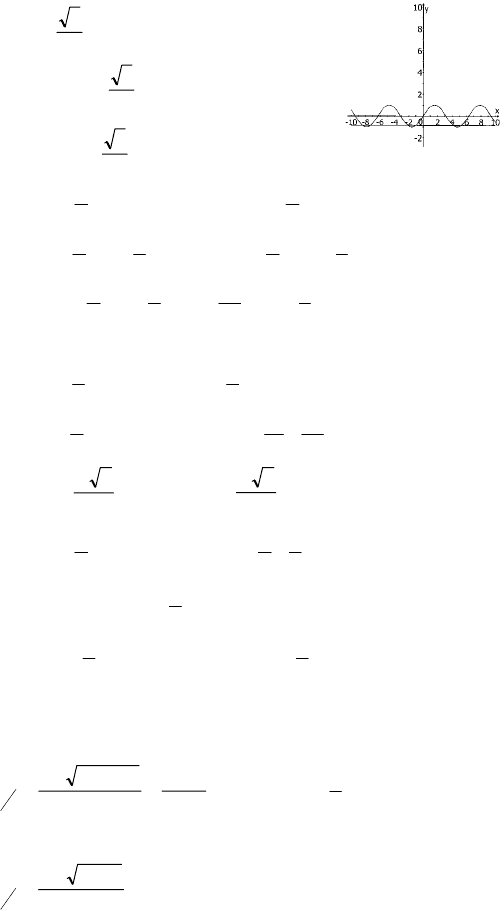
176
2)
2
3
sin −=x
[-π; 3π]
()
Znnx
n
∈π+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−= ,
2
3
arcsin1
()
Znnx
n
∈π+−=
+
,
2
3
arcsin1
1
()
Znnx
n
∈π+
π
−=
+
,
3
1
1
, n = 0,
3
π
−=x
,
n = -1,
π=π+
π
=
3
4
3
x
, n = 2,
π=π+
π
−=
3
5
2
3
x
,
Ответ:
π=π
−
=π=
π
−=
3
5
,
3
2
,
3
4
,
3
xxxx
.
№ 1178
1)
2
1
2sin =x
;
()
Znnx
n
∈π+−= ,
2
1
arcsin12
,
()
Znnx
n
∈π+
π
−= ,
6
12
,
()
Zn
n
x
n
∈
π
+
π
−= ,
212
1
;
2)
2
2
3cos
−
=x ;
Znnx ∈π+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
±= ,2
2
2
arccos3,
Znnx ∈π+
⎟
⎠
⎞
⎜
⎝
⎛
π
−π±= ,2
4
3,
Znnx ∈π+
π
±= ,
3
2
4
;
3) 2tg x + 5 = 0,
2
5
−=tgx
;
Znnarctgx ∈π+
⎟
⎠
⎞
⎜
⎝
⎛
−= ,
2
5
, Znnarctgx ∈π+−= ,
2
5
№ 1179
1) 3cos
2
x – 5cos x – 12 = 0.
Пусть cos x = a, тогда уравнение примет вид: 3а
2
– 5а – 12 = 0,
6
135
6
144255
2
1
±
=
+±
=a , а
1
= 3,
6
8
2
−=a
,
а
1
> 1, а
2
< –1 ⇒ исходное уравнение не имеет решений, т.к. |cos x| ≤ 1;
2) 3tg
2
x – 4tg x + 5 = 0, tg x = a, 3a
2
– 4a + 5 = 0,
3
1542
2
1
−±
=a ,
D < 0 ⇒ действительных корней нет.
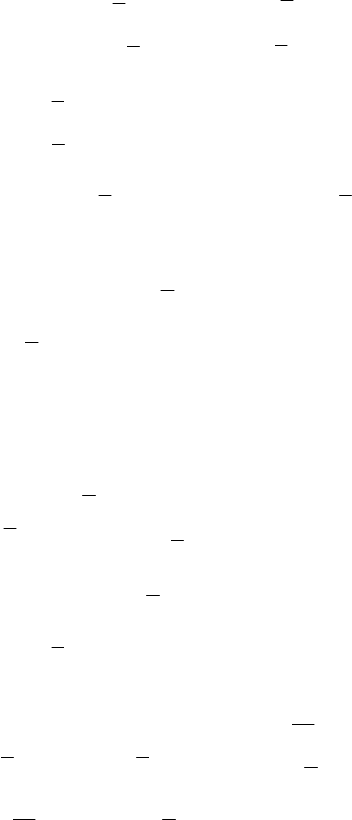
177
№ 1180
1) (3 – 4sinx)(3 + 4cosx) = 0,
⎢
⎣
⎡
=+
=−
0cos43
0sin43
x
x
;
⎢
⎢
⎢
⎢
⎣
⎡
−=
=
4
3
cos
4
3
sin
x
x
;
()
⎢
⎢
⎢
⎢
⎣
⎡
∈π+
⎟
⎠
⎞
⎜
⎝
⎛
−±=
∈π+−=
Zlx
Znnx
n
l ,2
4
3
arccos
,
4
3
arcsin1
;
()
(
⎢
⎢
⎢
⎢
⎣
⎡
∈π+−π±=
∈π+−=
Zlx
Znnx
n
l ,2
4
3
arcsin
,
4
3
arcsin1
.
Ответ:
()
Znnx
n
∈π+−= ,
4
3
arcsin1
,
(
Zlx ∈π+−π±= l ,2
4
3
arcsin
.
2) (tg x + 3)(tg x + 1) = 0,
⎢
⎣
⎡
=+
=+
01
03
tgx
tgx
;
⎢
⎣
⎡
−=
−=
1
3
tgx
tgx
;
⎢
⎢
⎣
⎡
∈π+
π
−=
∈π+−=
Zlx
Znnarctgx
l ,
4
,3
.
Ответ:
Zllx ∈π+
π
−= ,
4
; х = -arctg3 + nπ, n ∈ Z.
№ 1181
1) sin2x=3sin x cos
2
x, 2sin x⋅cos x–3sin x ⋅ cos
2
x, sin x⋅cos x(2-3cos x) = 0,
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−=
=
=
3
2
cos
0cos
0sin
x
x
x
;
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
∈π+
⎟
⎠
⎞
⎜
⎝
⎛
π±=
∈π+
π
=
∈π=
Zm ,2
3
2
arccos-x
Zl ,
2
x
Zn ,
m
l
nx
.
Ответ: x = nπ, n ∈ Z;
Zllx ∈π+
π
= ,
2
;
Zmmx ∈π+
⎟
⎠
⎞
⎜
⎝
⎛
−π±= ,2
3
2
arccos
2) sin4x = sin2x, 2sin2x ⋅ cos2x – sin2x = 0, sin2x(2cos2x – 1) = 0,
⎢
⎢
⎣
⎡
=
=
2
1
2cos
02sin
x
x
;
⎢
⎢
⎣
⎡
∈π+±=
∈π=
Zllx
Znnx
,2
2
1
arccos2
,2
⎢
⎢
⎢
⎢
⎣
⎡
∈π+
π
±=
∈
π
=
Zllx
Zn
n
x
,
6
,
2
Ответ:
Zn
n
x ∈
π
= ,
2
;
Zllx ∈π+
π
±= ,
6
.
3) cos2x + cos
2
x = 0, cos
2
x – sin
2
x + cos
2
x = 0, 2cos
2
x – 1 + cos
2
x = 0,
3cos
2
x = 1,
178
3
1
cos ±=x ,
⎢
⎢
⎢
⎢
⎣
⎡
∈π+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−π±=
∈π+±=
Zllx
Znnx
,2
3
1
arccos
,2
3
1
arccos
.
Ответ:
Znnx ∈π+±= ,2
3
1
arccos
, Zllx ∈π+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−π±= ,2
3
1
arccos
4) sin2x = cos
2
x, 2sin x ⋅ cos x – cos
2
x = 0, cos x(2sin x – cos x) = 0,
⎢
⎣
⎡
=−
=
0cossin2
0cos
xx
x
;
()
⎢
⎢
⎢
⎢
⎣
⎡
∈π+
π
−=
∈π+
π
=
Zllx
Znnx
l
,
6
12
,
2
;
()
⎢
⎢
⎢
⎢
⎣
⎡
∈
π
+
π
−=
∈
π
+
π
=
Zl
l
x
Zn
n
x
l
,
212
1
,
24
.
Ответ:
Znnx ∈π+
π
= ,
2
,
Zllarctgx ∈π+= ,
2
1
.
№ 1182
1) sin2x = 3cos x, 2sin x ⋅ cos x = 3cos x, cos x(2sin x – 3) = 0,
⎢
⎢
⎣
⎡
=
=
2
3
sin
0cos
x
x
;
⎢
⎢
⎣
⎡
φ∈
∈π+
π
=
x
Znnx ,
2
.
Ответ:
Znnx ∈π+
π
= ,
2
.
2) sin4x = cos
4
x – sin
4
x, 2sin2x ⋅ cos2x = (cos
2
x – sin
2
x)(sin
2
x + cos
2
x),
2sin2x ⋅ cos2x = cos2x, cos2x(2sin2x – 1) = 0,
⎢
⎢
⎣
⎡
=
=
2
1
2sin
02cos
x
x
;
()
⎢
⎢
⎢
⎢
⎣
⎡
∈π+
π
−=
∈π+
π
=
Zllx
Znnx
l
,
6
12
,
2
2
;
()
⎢
⎢
⎢
⎢
⎣
⎡
∈
π
+
π
=
∈
π
+
π
=
Zl
l
n
x
l
,
212
1-x
Zn ,
24
Ответ:
Zn
n
x ∈
π
+
π
= ,
24
,
()
Zl
l
x
l
∈
π
+
π
−= ,
212
1
.
3) 2cos
2
x = 1 + 4sin2x, (2cos
2
x – 1) = 4sin2x, cos2x = 4sin2x,
4
2sin
2cos
=
x
x
; ctg x = 4; x = arcctg4 + nπ, n ∈ Z.
Ответ: x = arcctg4 + nπ, n ∈ Z
4) 2cos x + cos2x = 2sin x, 2(cos x – sin x) + (cos
2
x – sin
2
x) = 0,
2(cos x – sin x) + (cos x – sin x)(cos x – sin x) = 0,
(cos x – sin x)(2 + cos x + sin x) = 0,
⎢
⎣
⎡
−=+
=−
2sincos
0sincos
xx
xx
;
Znnx ∈π+
π
= ,
4
x ∈
φ
Ответ:
Znnx ∈π+
π
= ,
4
.
179
№ 1183
1) cos x + cos2x = 0, 0
2
cos
2
3
cos2 =⋅
x
x ,
⎢
⎢
⎢
⎢
⎣
⎡
=
=
0
2
cos
0
2
3
cos
x
x
⎢
⎢
⎢
⎢
⎣
⎡
∈π+
π
=
∈π+
π
=
Zll
x
Znnx
,
22
,
22
3
⎢
⎢
⎣
⎡
∈π+π=
∈π+
π
=
Zllx
Znnx
,2
,
3
2
3
Ответ:
Znnx ∈π+
π
= ,
3
2
3
; x = π + 2lπ, l ∈ Z.
2) cos x – cos5x = 0, -2sin3x ⋅ sin(-2x) = 0,
⎢
⎣
⎡
=
=
02sin
03sin
x
x
;
⎢
⎢
⎢
⎢
⎣
⎡
∈
π
=
∈
π
=
Zl
l
x
Zn
n
x
,
2
,
3
.
Ответ:
Zl
l
x
n
x ∈
π
=
π
= ,
2
,
3
.
3) sin3x + sin x = 2sin2x
2sin2x ⋅ cos x = 2sin2x, 2sin2x(cos x – 1) = 0,
⎢
⎣
⎡
=
=
1cos
02sin
x
x
⎢
⎢
⎣
⎡
∈π=
∈
π
=
Zmmx
Zn
n
x
,2
,
2
.
Ответ:
Zn
n
x ∈
π
= ,
2
.
4) sin x+sin2x+sin3x = 0, 2sin2x ⋅ cos x + sin2x = 0, sin2x(2cos x + 1 ) = 0,
⎢
⎢
⎣
⎡
−=
=
2
1
cos
02sin
x
x
;
⎢
⎢
⎢
⎢
⎣
⎡
∈π+
⎟
⎠
⎞
⎜
⎝
⎛
π
−π±=
∈
π
=
Zllx
Zn
n
x
,2
3
,
2
Ответ:
Znnx
n
x ∈π+π±=
π
= ,2
3
2
;
2
.
№ 1184
1) 2cos x + sin x = 0, 2 + tg x = 0, tg x = -2, x = -arctg2 + nπ, n ∈ Z.
Ответ: x = -arctg2 + nπ, n ∈ Z.
2) 0cos3sin =+ xx , 3−=tgx ,
Znnarctgx ∈π+−= ,3,
Znnx ∈π+
π
−= ,
3
.
Ответ:
Znnx ∈π+
π
−= ,
3
.
