Johnson R.S. A Modern Introduction to the Mathematical Theory of Water Waves

Подождите немного. Документ загружается.

104 2 Some classical problems in water-wave theory

since there is no variation in Y. Near the shoreline we have D -> 0 and

a -> oo, but with oD -> 0, as we see from equation (2.96), which then

gives

= 8

and

dco

^ 8

kco ^kD ^oD

dk a

(o 8co

since k ~ a/8 as a -> oo (from or = <5 JA;

/Q).

Hence, using equation

(2.98),

we see that

A = O(ZT

1/4

) as D -* 0

which is Green's law again (see equation (2.46), et seq., and Q2.34). Also,

since k -> oo as

-> 0, the waves approaching the shoreline get shorter,

as we have already discussed in Section 2.2; this phenomenon is included

in Figure 2.6. (We should recall the warnings given in Section 2.2 con-

cerning the dubious validity of the linear equations as the depth decreases

to zero.)

Finally, we consider a wave which is propagating in a region

where the depth is D = D

, for 0 < X < X

let us say. For X < 0

and X > X

the depth increases (so that D = D

, 0 < X < X

, describes

a submerged ridge); as before, we then have

/JL/8

= /

and

cP-iX) =

+ fi

+ ig), given that k = (fc

, /

) in 0 < X < X

As the depth increases so a decreases, and if it drops sufficiently so

that a

< /x

then equation (2.97) shows that the wavefronts no

longer exist. Of course, exactly the same can be said of the rays. Indeed,

at the points where a

/JL

the slope of the rays becomes infinite and this

will happen for all rays; the lines along which a

/JL

are called caustics

(and are, perhaps, familiar from the theory of geometrical optics). The

caustic is therefore the envelope of the rays. The continuation of a ray,

beyond the point where &Y/&X on it becomes infinite, is possible by

switching to the other sign in the equation of the ray, (2.95), and produ-

cing it back into the region where the depth decreases. If this phenom-

enon occurs in both X < 0 and X > X

, then the surface wave over depth

D = D

remains trapped in a region containing the ridge; it is called a

trapped wave, and this is depicted in Figure 2.7.

The caustic is where a

—

/JL

h?'

-> 0, and so dco/dk -> 0; see equa-

tion (2.84) and remember that co is constant and that both a and D

approach finite (nonzero) values at the caustic. Hence equation (2.98)

Ray theory for a slowly varying environment 105

Surface

Figure 2.7. The rays and wavefronts for waves trapped between caustics (which

are represented by the dashed lines).

shows that the amplitude of the wave diverges at the caustic, so our

simple linear theory is no longer adequate. Some appropriate higher-

order effects must be invoked in the neighbourhood of the caustic in

order to produce a theory in which the wave amplitude remains finite.

This more detailed discussion is not pursued here, but some further

reading in this direction is mentioned at the end of the chapter.

2.3.2 Ray theory in cylindrical geometry

The equations and examples that we have presented so far have been

written in rectangular Cartesian coordinates. However, problems that

involve cylindrical surface waves or circular depth contours are clearly

best discussed in cylindrical polar coordinates. Rather than derive the

relevant equations from first principles, we follow the far simpler route of

merely transforming the equations that we already have, according to

106

Some

classical problems

in water-wave theory

X = RcosO,

= RsinO.

Here, R is the radial coordinate suitably scaled like both

and F, that is,

R =

ccr;

the angular variable, 0, obviously requires no scaling. The phase

function then satisfies

|k| cos(

0),

|k| sin(x

0) (2.99)

since,

the constant state,

takes the form

0 =

\k\Rcos(x-0)-coT

= (|k| cos

x)i*

cos 0

(|k| sin x)R sin 6

coT,

where

is a constant and the phase function is written as 0, and only this

form will

used here

order

avoid

the

obvious confusion with

the angular variable 0. The wave-number vector

cylindrical polars

written using the same notation as earlier,

(k,

0 [=

|k|{cos(x

0),

sin(x

0)}

from above].

Thus we obtain

which is obviously the polar form of equation (2.89). The corresponding

equation for the action is, from equation (2.86),

where the group velocity is written as c

) in cylindrical polars.

Similar to our discussion in Section

2.3.1,

let us consider steady wave

propagation over

depth variation which depends only

on R, so

that

D = D(R). The dispersion relation is unchanged:

tanh(orD) with

8y/k

since the derivation leading to these (given earlier as equations (2.78) and

(2.76)) does

not

involve derivatives with respect

to the

slow scales.

(Remember that we have used

the

same notation here

for

the wave-

number vector,

and so

|k|

is the

relevant expression.)

For

the analogue

of a

submerged ridge (which was discussed above),

now have

shoal with cylindrical symmetry (with the origin of coordi-

nates chosen so that

0 is the centre of the shoal); the minimum depth

Ray

theory

for

slowly varying

environment

107

occurs

at the

centre

of the

shoal.

The

wavefronts

are

described

constant, where

(2.102)

cf. equation (2.94). Correspondingly, the equations

for

the rays

(at

fixed

T) become

constant; (2.103)

cf. equation (2.95),

and

remember that

the

orthogonality

two curves

(r =f(0),

g(0)),

written

polar coordinates, requires that

f\e)g\e)

-?.

Let

suppose that Ra(R)

monotonic

in R

(which will certainly

describe

class

circular shoals).

On the

rays we have

= ±fiRy/R

-n

(2.104)

and

a ray

approaching

the

shoal must have either dR/dO

> 0 or

dR/dO

0; then

decreases

either

decreases

increases, respec-

tively. This obtains until the ray reaches

minimum distance from

R = 0,

which occurs where

£-0

«V-»»

on the ray; thereafter

increases, which

accommodated

switching

the

other sign

equation (2.104). This type

solution,

for two

different rays

(one

with dR/dO >

initially, that

is, to the

left,

the

other with dR/dO

< 0) is

shown

Figure 2.8. Two important observa-

tions

can now be

made: first,

as the

depth decreases,

so the

rays turn

towards the centre of the shoal until they reach

minimum distance from

and

then they turn away. This general description

what

should expect, based

on the

corresponding problems with

D =

D(X)

given

Section

2.3.1.

Second, we see that

consequence

the bending

of the rays is that,

the lee

the shoal (that is, 'behind'), the rays

and

wavefronts,

course

cross. Where these waves intersect there may

either

constructive

or a

destructive interaction;

peak plus

peak

(or

trough plus trough) is constructive, but

peak plus

trough will

at least

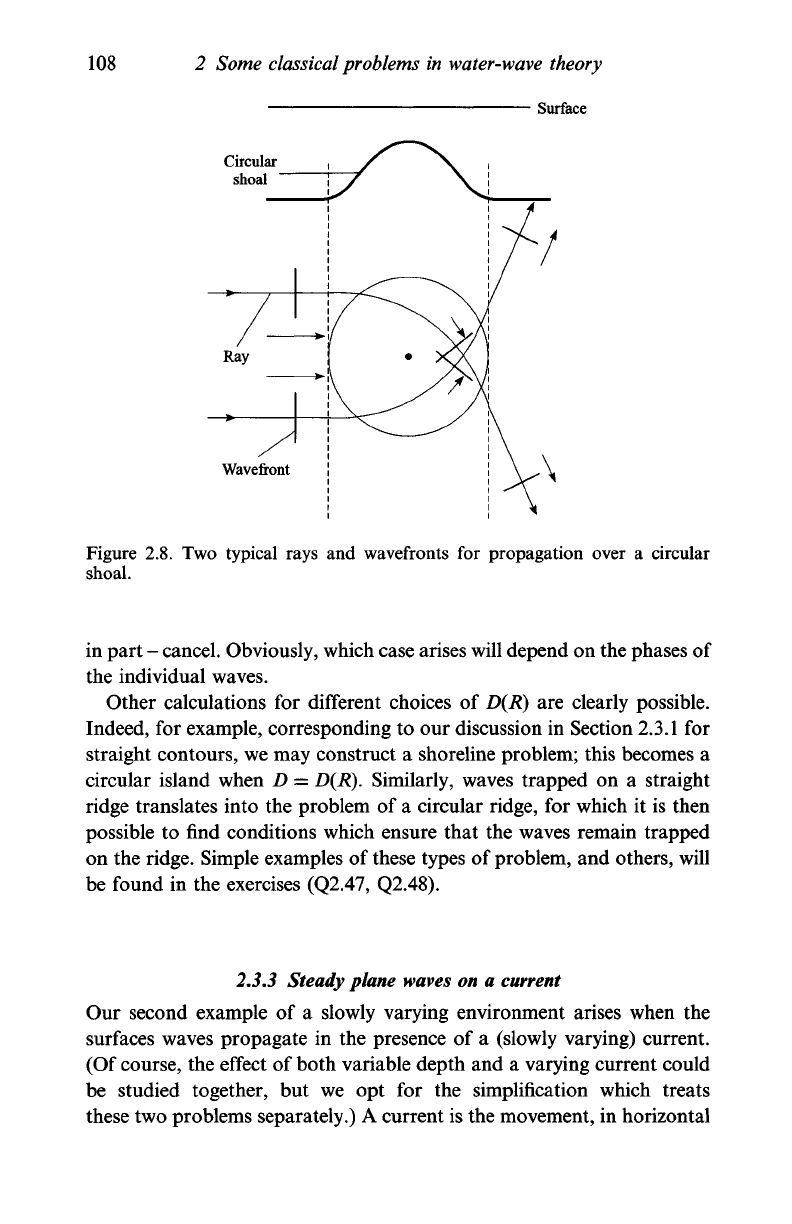
108 2 Some classical problems in water-wave theory

Surface

Circular

shoal

Wavefront

Figure 2.8. Two typical rays and wavefronts for propagation over a circular

shoal.

in part - cancel. Obviously, which case arises will depend on the phases of

the individual waves.

Other calculations for different choices of D(R) are clearly possible.

Indeed, for example, corresponding to our discussion in Section 2.3.1 for

straight contours, we may construct a shoreline problem; this becomes a

circular island when D = D(R). Similarly, waves trapped on a straight

ridge translates into the problem of a circular ridge, for which it is then

possible to find conditions which ensure that the waves remain trapped

on the ridge. Simple examples of these types of problem, and others, will

be found in the exercises (Q2.47, Q2.48).

2.3.3 Steady plane waves on a current

Our second example of a slowly varying environment arises when the

surfaces waves propagate in the presence of a (slowly varying) current.

(Of course, the effect of both variable depth and a varying current could

be studied together, but we opt for the simplification which treats

these two problems separately.) A current is the movement, in horizontal

Ray theory for a

slowly varying environment

109

directions, of a body of water (but, in order to maintain the condition of

mass conservation, some vertical motion may also be present); we shall

treat the current as a prescribed ambient state which is then perturbed by

the surface waves. These motions are, in general, rotational, and so we

must use the Euler equation (rather than Laplace's equation). In

Cartesian geometry, we therefore start with the problem described by

the equations (1.57) and (1.63)-(1.65)

namely

_ dp Dv _ dp

Dw__ dp

du dv dw

—+ —+ — = 0,

dx dy dz

with

= H

and p = H on z =

and

w = 0 on z = 0.

Here we have chosen to consider only gravity waves (so that the Weber

number, W, is set to zero) and the bottom is z = b = 0; we have written

ST]

= H. It is seen that we have not quoted the corresponding scaled

equations ((1.67), (1.69), (1.70)) for these cannot accommodate the

imposed current; cf. Q2.ll and Q2.12.

The relevant form of the governing equations required here - that is,

linearised about the ambient state - is obtained (cf. Section

1.3.3)

transforming

w -> W

where (Uj_, W) represents the current; this state must satisfy the

equations with e = 0, so we also require

Thus,

with uj_ = (£/, F), we have

dP DK_ dP

T>W _ dP

~Tn~~~d'

~Df~~~d

where

D d . „ d . „ d . „ d

(2.105)

with

110 2 Some

classical problems

water-wave

theory

dU dV W

+ + 0

and

W = H

+ VH

, P = H on z =

+ H;

W = 0 onz = 0,

for the current alone. Note that, in general, in the presence of a current,

the undisturbed surface is not a z = constant surface. We now restrict

consideration to a current which is steady but which slowly varies in the

horizontal directions; thus we regard U

, W, P, and H as functions of

(ax, ay), and z as appropriate, with a -> 0 (which corresponds to the

choice made in Section 2.3.1). It is clear from the equation of mass

conservation (in (2.105)) that W = O(a); consequently any upwelling or

down-currents are weak (although necessarily present, in general).

The linearised equations for the surface wave are now obtained by

collecting the leading-order terms as 6 -> 0 (from the governing equa-

tions),

but after we have satisfied equations (2.105) for the current. This

leads to the set of equations

+ (u-

where

with

w + r)W

•=

+ Ur\

Vr]

+ uH

+ vH

onz=l+H

and

—

0 on z = 0.

We seek a solution of this linearised problem in the form of asymptotic

expansions valid as a -> 0, just as we did for the case of variable depth.

To this end (cf. equations (2.71)-(2.73)) we write

X = ax, Y = ay, T = at,

Ray theory for a slowly varying environment 111

and

(Ox,

Oy)

= W*. Y, T), l(X, Y, T)},

-co(X,

Y, T)

which produces the set

—

COUQ

+ U(au

+ ku

) + V(au

+ lu

)

W^M

H-

a(uU

+ vC/

) + wt/

= —(ap

^/?6>);

+ Wv

ot(uV

H-

^^y) + wF

= —(apy +

^P6>)»

{aw

— ce^Wgi

+ t/(aw

fcwg,)

+ V(aw

/H^)

+ PFw

ot(uW

+ vW

) + wW

) = —p

+ fog + w

+ a(w^ + ^r)

with

w + t)W

= arj

corj

+ t/(a^ + kr)

)

+ V(arj

+ /r/g) +

a(uH

+ v^r) on z =

+ H

p = rj-rjP

and

= 0 on z = 0.

Further, in order to make the problem a little more manageable, we shall

assume that the horizontal components of the current depend only on

(X, Y), at least to O(a

), and therefore not z. Thus, from equations

(2.105),

we obtain

so that H{X, Y\ a) satisfies

{(1 + H)U}

{(1

+ H)V}

= O(a

)

and then

P = H + O(a

) for 0 < z <

+ H.

The expression for W describes the upwelling (or down current) asso-

ciated with the current; it is absent at this order only if the current

satisfies U

+ V

= 0.

The solution that we seek comprises a single harmonic component, and

so we write

Q ~ (Go + <*ei)e

+ ex. + O(a

112 2 Some classical problems in water-wave theory

where Q represents each of u, v,

p, and

rj.

The leading-order problem

then becomes

-cou

4- Uku

+ Vlu

= -kp

;

-cov

+ Ukv

4- Kfo

—Ipol

(-cow

+ C/fcw

+ Vlw

) = -p

;

i(ku

+ Iv

) + w

= 0,

with

= -ia)ri

+ \kUri

+ilVri

\ on z = I + H

and

= 0 on z = 0.

Thus

where we have written

Q =

o)-kU-lV

(2.106)

and then

^ + w

, = 0; i<5

£2H>

= p

so that

cf. equation (2.74). The boundary conditions for w

are

= — iQrj

on z = 1 + H\ w

= 0 on z = 0

which require

sinh(orz)

where

Ray theory for a slowly varying environment 113

exactly as before (equations (2.76)). Finally, from

8rj

cosh(az)

Po =

sinh{or(l

and the boundary condition on p

, we obtain the familiar dispersion

relation

(co

- kU - IV)

= ^tanh{<r(l +

77)},

(2.107)

where Q replaces

co;

see equation (2.78) and Q2.12.

We now proceed to the next order, but we shall describe the calculation

in outline only. The technique follows precisely that presented for the

case of slowly varying depth (given in equations (2.79)-(2.81) et

seq.).

Furthermore, the results are essentially identical to those obtained pre-

viously, the difference arising from the appearance of Q (for co), for

example. The equations at O(a) take the form

= Qui + F

; lp

= Qv

{

+ F

; p

= i

with

= — itlrji + F

and p

rji

on z =

+ 77,

and

= 0 on z = 0,

where the forcing terms, F

—

1,..., 5), depend on the leading-order

solution. These produce an equation for w

of the form

lzz

- h\k

+ /Vi = G,

where G depends on the F

. Rather than solve for w

we multiply by w

and integrate with respect to z, 0 < z <

77;

cf. equation (2.82) et seq.,

to see how this will produce the equation for

(X,

Y, T) (which is the

first term in the asymptotic expansion of the (complex) amplitude of the

surface wave).

As before, this equation for rj

is far more usefully written in terms of

the energy, E; cf. equation (2.85). We then find directly (although the

details are rather tiresome and are left as an exercise) that, corresponding

to equation (2.86), E satisfies

(|)0. (2.108,