Johnson R.S. A Modern Introduction to the Mathematical Theory of Water Waves

Подождите немного. Документ загружается.

124

Some

classical

problems in water-wave theory

where

have

set

0(x^, h

, 0)

as we may

always

do.

Now,

for a

finite-amplitude surface wave we must have

jr]dt->0

as T

but

for an

impulse we require

j(P

-P

)dt

to have

finite

and

nonzero limit

as T -> 0

;

this

is the

impulsive

pres-

sure. Hence the required initial condition (for the concentric wave) is that

0(x

, h

, 0) is to be specified. This condition is to be incorporated into the

determination

rj(r,

(where

(r, 0),

and

there

is no

dependence

here

on 0).

clear that 0(r,

1,0

satisfies

the

same wave equation

rj(r,t),

equation (2.14), essentially

virtue

the boundary condition

cj)

0 on z = 1;

see equation (2.67)

(and

note that

have reverted

to our non-

dimensional variables). Thus, immediately,

have

the

appropriate

solution

for 0 (cf.

equation (2.30))

where

t) =

Jpf(p)

1,0)

= J

cos(t^\j

(rp)

pf(p)J

(rp) dp =/(r),

say,

and

rj(r,

—

(r,

1, 0)

The

impulse that

we use (a

point

impulse)

modelled

0 < r

0, r>a~

The

ship-wave

pattern 125

with a -> 0, so that

(pr)dr

= lfrJ

(

—•

I ydy = -la

as a -> 0,

if /a

is fixed. (We have written r

—

ay here and used the familiar result

Jo(x) -> 1 as x -> 0.) Thus, with/(p) = \la

= & say, we obtain

»7(r,

0 -

-0,(r,

0 = ^//

*in(tJf)Jo(rp)dp (2.114)

(from which we can determine the corresponding form taken by

77,(

0);

cf. Q2.19)). It is this solution, (2.114), for concentric waves on deep water

generated by a point impulse, which we now examine.

This first stage of the calculation follows precisely that presented in

Section

2.1.3.

We introduce the integral representation of J

(see equation

(2.31)) and then write

as the real part of the sum of two integrals (as in

equation (2.32). This is transformed according to

and then we use Kelvin's method of stationary phase for a

->•

oo to give

(2.115)

cf. equation (2.36). This calculation, which parallels that described in

Section

2.1.3,

is left as an exercise (Q2.50). Our task now is to incorporate

this result into a description of the waves generated when the point

impulse moves along a prescribed path.

The point impulse - a ship, perhaps - moves on the surface of

the

water

along a path F, described in Cartesian coordinates by

(X(t),

Y(t)l

where t is the time elapsed since the ship (let us call it that) was at the

point P', namely at (X, Y); the ship is now at P, the origin of coordinates.

The path is assumed smooth (so that both X(t) and Y(t) are (at least)

once-differentiable functions) and then the X-axis is chosen to be tangent

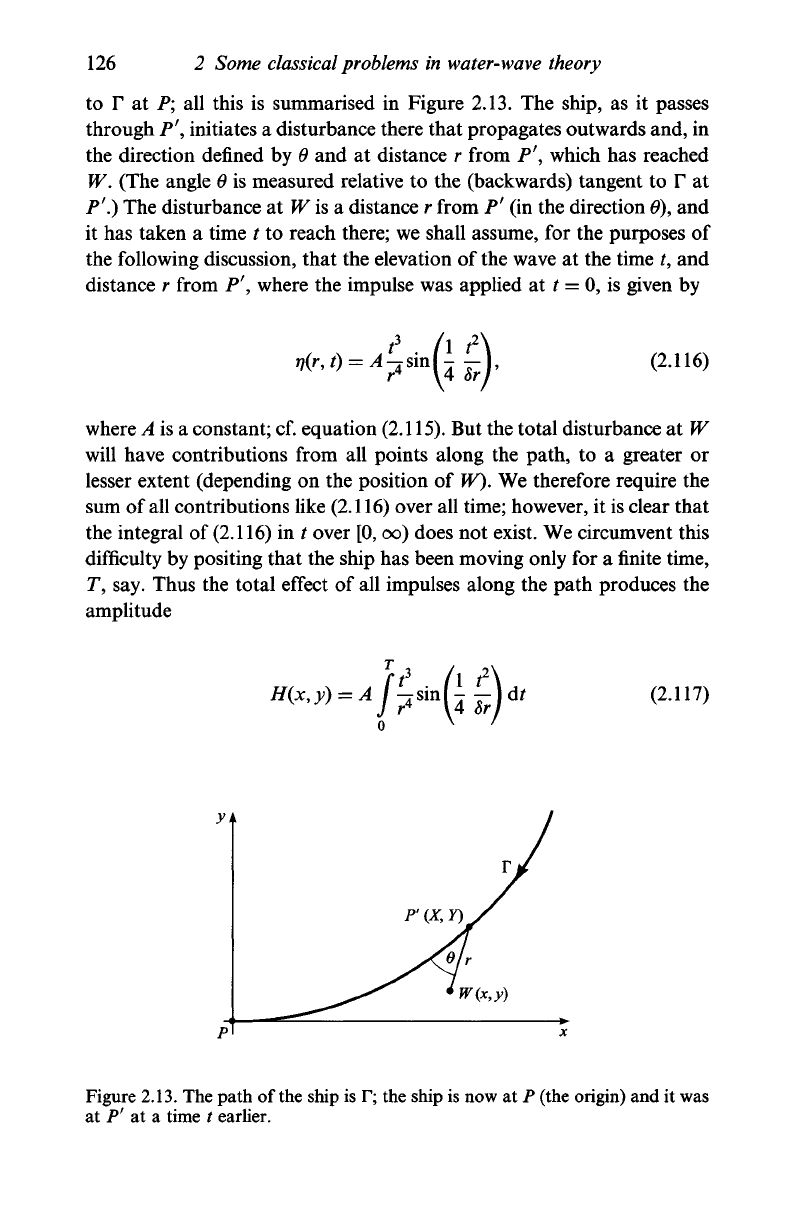
126

2 Some classical problems in water-wave theory

to F at P; all this is summarised in Figure 2.13. The ship, as it passes

through P\ initiates a disturbance there that propagates outwards and, in

the direction defined by 0 and at distance r from P\ which has reached

W. (The angle 0 is measured relative to the (backwards) tangent to r at

The disturbance at W is a distance r from P' (in the direction

0),

and

it has taken a time t to reach there; we shall assume, for the purposes of

the following discussion, that the elevation of the wave at the time t, and

distance r from P\ where the impulse was applied at t = 0, is given by

r,t) = A-g (2.116)

where A is a constant; cf. equation

(2.115).

But the total disturbance at W

will have contributions from all points along the path, to a greater or

lesser extent (depending on the position of W). We therefore require the

sum of

all

contributions like (2.116) over all time; however, it is clear that

the integral of (2.116) in t over

[0,

oo) does not exist. We circumvent this

difficulty by positing that the ship has been moving only for a finite time,

T, say. Thus the total effect of all impulses along the path produces the

amplitude

(2.117)

Figure

2.13.

The path of the ship is F; the ship is now at P (the origin) and it was

at P' at a time t earlier.

The

ship-wave

pattern

127

where

= (x - X{i)f + (y - Y(i)f. (It is

clear that this integral

also does

not

exist

for

points on

the

ship's path, where

r =

0; however,

the

method

stationary phase that

led to

(2.115)

has

already been inter-

preted only

for

points away from

r =

we are

seeking

the

wave pattern

as seen some distance from

the

ship.)

To proceed,

express (2.117)

in the

form

H(x,y)

= AA

/^exp(U

/4Sr)df

(2.118)

and

have previously used

—

P'/Sr

-» oo;

thus

we may

apply

the

method

stationary phase

yet

once more!

The

point(s)

stationary

phase occur where

m--

for

r = r(0,

UM r /

at fixed

y: thus

? =

-•

(2-119)

v J

(The fact that

we are

treating

o =

cr(t),

and a -> oo is

required

for the

method

stationary phase,

irrelevant

in the

application

of the

method.)

But

from

we have

(at

fixed

(JC,

y))

_dt' dt)

= rU(t)cosO,

where

U{i)

(= ^(dX/dtf + (dY/dtf) is the speed of the ship, so (since

^=UcosO. (2.120)

Thus

the

condition

stationary phase, (2.119), becomes

= ^Utcos$,

(2.121)

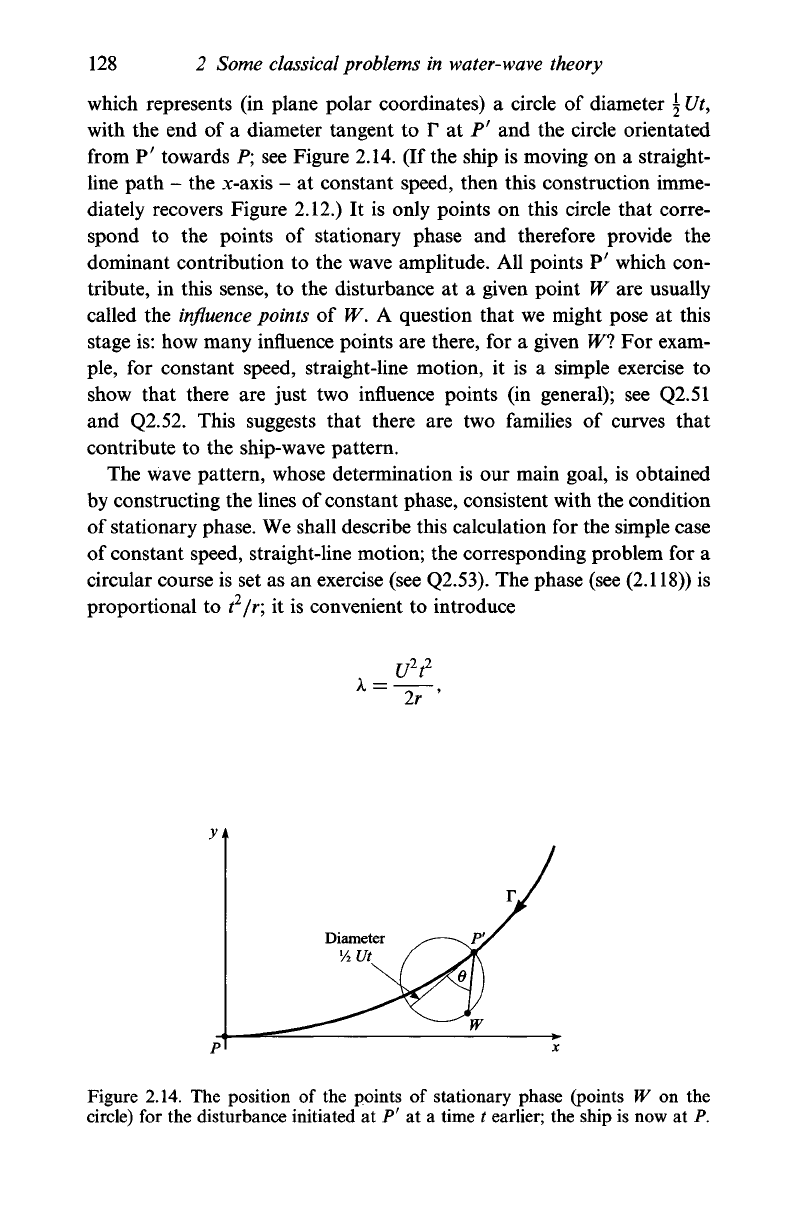
128

2 Some classical problems in water-wave theory

which represents (in plane polar coordinates) a circle of diameter \ Ut,

with the end of a diameter tangent to r at P

and the circle orientated

from P' towards P; see Figure 2.14. (If the ship is moving on a straight-

line path - the x-axis - at constant speed, then this construction imme-

diately recovers Figure 2.12.) It is only points on this circle that corre-

spond to the points of stationary phase and therefore provide the

dominant contribution to the wave amplitude. All points P' which con-

tribute, in this sense, to the disturbance at a given point W are usually

called the

influence

points of W. A question that we might pose at this

stage is: how many influence points are there, for a given Wl For exam-

ple,

for constant speed, straight-line motion, it is a simple exercise to

show that there are just two influence points (in general); see Q2.51

and Q2.52. This suggests that there are two families of curves that

contribute to the ship-wave pattern.

The wave pattern, whose determination is our main goal, is obtained

by constructing the lines of constant phase, consistent with the condition

of stationary phase. We shall describe this calculation for the simple case

of constant speed, straight-line motion; the corresponding problem for a

circular course is set as an exercise (see Q2.53). The phase (see (2.118)) is

proportional to t

/r; it is convenient to introduce

2r '

Figure 2.14. The position of the points of stationary phase (points W on the

circle) for the disturbance initiated at P' at a time t earlier; the ship is now at P.

The

ship-wave pattern

129

where U is the constant speed of the ship, and then

= constant yields

the curves of constant phase. But the condition of stationary phase, from

(2.121),

yields

rUt =

-U

cos 0

= kr

cos 0

Ut = kcosO,

and then

r = -UtcosO = -Acos

(2.122)

(In fact, the equations (2.122) are valid for any path and, indeed, in the

construction of

these

equations we may allow U =

U(t).)

The path here is

simply

X = Ut, Y = 0,

and then any point W is

x = Ut

—

cos 0,

y =

—r

sin 0,

where r and

are shown in Figure

2.13.

Thus, using equations (2.122), we

obtain directly

x = A(cos0--cos

0), y = - - k

cos

0 sin

(2.123)

which are the parametric equations (parameter

for the dominant con-

tribution to the wave pattern, each wave crest/trough being associated

with a fixed value of

The pattern of wave crests (or troughs) is shown in

Figure

2.15,

which closely resembles the wave pattern produced in nature;

compare this figure with Figure 2.10. Note that in this figure we

have included points r = 0 (which do exist on the curve (2.123)) for

completeness only.

Before we leave our discussion of

this

pattern, we comment that Figure

2.15 plainly shows two families of curves (exactly as we observe) which

meet on the boundary of the region. Where these two families meet is

quite significant; consider the derivatives obtained from equations

(2.123):

dx 3 i 1 i

— = X(-

sinO

+ -cos

0sin0) = -A(1 - 3sin

6)sin0

Q.0 2 2

130 2 Some classical problems in water-wave theory

0.3-

0.2-

o.i-

Transverse system

0.2 0.4

0.6 0.8

Figure 2.15. The ship-wave pattern as obtained from equations (2.123), for var-

ious values of k

0.5,1,1.5,2); the fine line denotes the boundary of the wedge

which contains the dominant contributions.

and

^ = -1 A,(cos

0 - 2 cos 0 sin

0) = - \k{\ - 3 sin

cos 0.

2 2

It is clear that dy/dx is singular at 0 = 0 (which is where all curves meet at

P) and also where 3 sin

0—1=0; this defines the angle

that is attained

where the two influence points coincide (and we note that this is the same

for all waves, since it is independent of

A).

This and other relevant points

are included in Figure 2.15; in particular we see that the two families are

defined by 0 < 0 < 0

and 0

< 0 <

TT/2,

respectively.

Finally, we make full use of Kelvin's method of stationary phase in

order to provide an estimate for the wave amplitude along the lines of

constant phase where the dominant contributions occur. To this end, we

use the general result given in equation (2.35) and apply it to the integral

in (2.118). Thus we require

The ship-wave pattern 131

evaluated at the points of stationary phase; first we have

\ r) ~ dt\

dt) r r

\dt) r

which, on lines dr/dt = 2r/t (equation (2.119), for stationary phase),

yields the expression

-A.

(1,24)

But on these lines we also have, (2.120),

which gives

— = UcosO,

d0 . „

since U = constant; now we must find dO/dt.

For the straight-line course (along y = Y = 0), at constant speed U, we

see that (cf. Figure 2.13)

0 + arctanf—-—\ =

\Ut - x)

with X = Ut. Thus, at fixed (x, y), we obtain

dO yU

= Q

(x-utf+y

and we also have sin(7T

—

0) = —y/r where r

= (x

—

Ut)

; hence

and so

dO U .

— = sin 0

dt r

r U

-—.

= —sin 0.

The expression (2.124) therefore becomes

= -(1 - 3 sin

6)/cos

6, (2.125)

132

Some classical problems

water-wave theory

which

observe

zero

±arcsin(l/\/3)) where

the two

families of wave crests/troughs meet. Further, we must include two domi-

nant contributions

to the

wave amplitude

- one

from each family

(although, perhaps,

we may

find that

one of

these dominates

the

other).

Since

the two

families

are

generated

(in y > 0) by 0 < 0

< 6

and 0

n/2,

respectively, we see from (2.125) that

and

—j

l-\ < 0 for

< 0 <

7r/2.

For

given point,

W, we let the

contribution

in the

range

0 < 0

< 0

usually called the

transverse

wave system

be designated by the subscript

t, and for the

other contribution, usually called

the

diverging

system,

shall write

the

subscript d; this terminology

used

Figure 2.15.

The

two

terms that provide

the

dominant asymptotic behaviour

(as

/8r

oo), according

Kelvin's result (2.35), therefore yield (after

little manipulation)

±1

fn cos

Gxp{i(r/8a

TT/4)}

a]yj\ -

3 sin

fn cos 0

exp{i(r/8o% -

TV/4)}

-1

(2.126)

Here, we have substituted

for

time

from (2.121)

and

written

=-UcosO

= t,d).

The solution expressed by (2.126) is the final result that we present in this

section.

We see

that both contributions

are of

the same order, that

the

amplitude decays like r~

1/2

away from the ship's path, but that the ampli-

tude

undefined where

the two

families meet

(at 0

= arcsin(l/>/3)).

(The

amplitude

also undefined where

= n/2, but

this

is at

P, the origin, and is

be expected because

the nature

our

point impulse model.)

analysis

can be

performed,

taking Kelvin's

method

stationary phase

to the

next order,

for the

case

;

The

ship-wave pattern

133

the wave amplitude can then be shown to be

finite

but now it behaves like

1/3

away from the ship's path. This goes some way to explaining why

the waves near the edge of the wedge-shaped region are observed so

readily: they are larger than those nearby and on each of the families

separately. Finally, we note that the two systems of waves, transverse and

diverging, have a phase difference of n/2 even when ct

« a

. Thus we

anticipate that near the edge of the wedge, where a

and a

are nearly

equal, a phase difference will be evident; this is, indeed, seen in well-

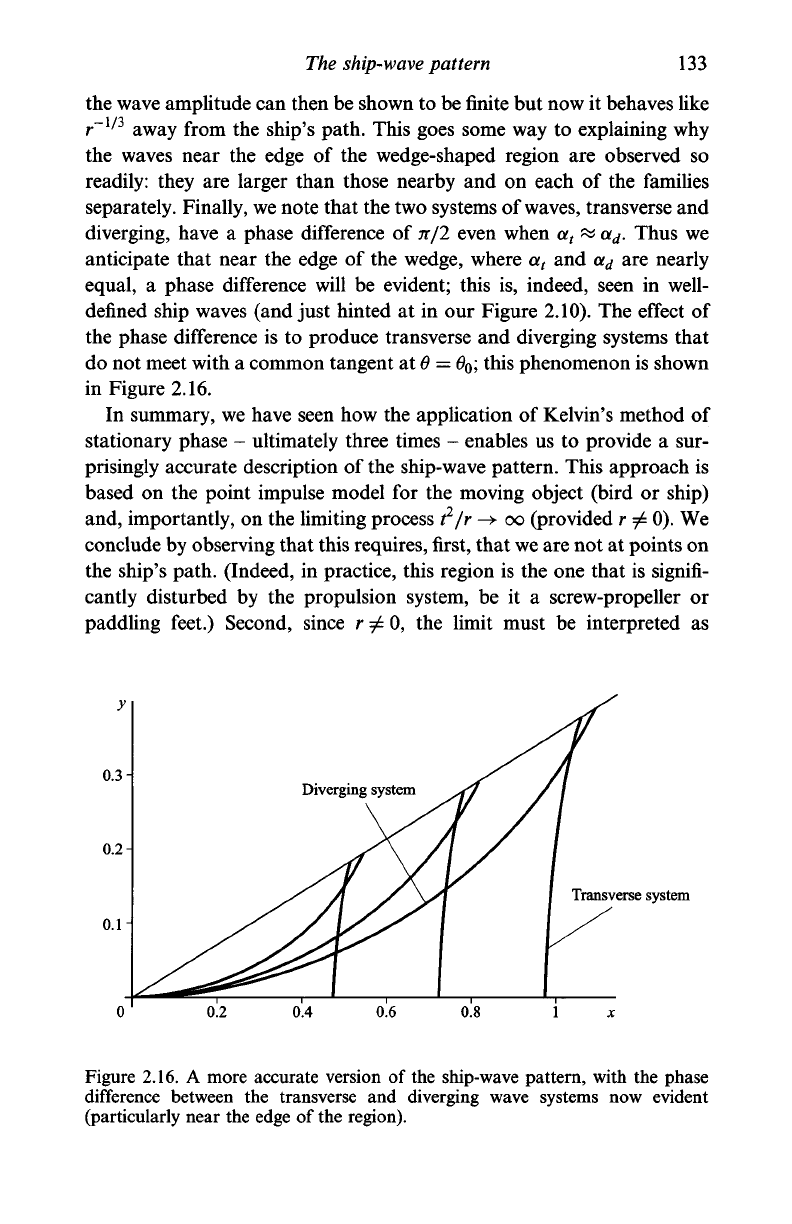
defined ship waves (and just hinted at in our Figure 2.10). The effect of

the phase difference is to produce transverse and diverging systems that

do not meet with a common tangent at

;

this phenomenon is shown

in Figure 2.16.

In summary, we have seen how the application of Kelvin's method of

stationary phase - ultimately three times - enables us to provide a sur-

prisingly accurate description of the ship-wave pattern. This approach is

based on the point impulse model for the moving object (bird or ship)

and, importantly, on the limiting process t

/r -» oo (provided r ^ 0). We

conclude by observing that this requires, first, that

are not at points on

the ship's path. (Indeed, in practice, this region is the one that is signifi-

cantly disturbed by the propulsion system, be it a screw-propeller or

paddling feet.) Second, since r ^ 0, the limit must be interpreted as

Transverse system

0.2 0.4 0.6 0.8

Figure 2.16. A more accurate version of the ship-wave pattern, with the phase

difference between the transverse and diverging wave systems now evident

(particularly near the edge of the region).