Johnson R.S. A Modern Introduction to the Mathematical Theory of Water Waves

Подождите немного. Документ загружается.

74 2 Some classical problems in water-wave theory

2n/k

0 0

where we have retained both the kinetic and potential contributions to

the energy (although these are of different orders of magnitude as s -> 0).

It follows directly that we have

2n/k {

27t

M ,2

where the term (n/k) represents the potential energy of the undisturbed

fluid. (Because of our choice here of computing the energy in one period,

this potential energy depends on the wavelength through k; it is quite

usual, therefore, to define an average energy over one period:

2n/k

The second term is associated with the wave motion alone; because of our

scaling, it is proportional to e

(as e -• 0) - which is to be expected - and

it is also proportional to

the required result.

Finally, we briefly describe the particular form that c

takes for our

water-wave problem, and what this implies for the propagation of waves.

We already have (from equation (2.9)) the dispersion relation

= A

It is left as an exercise (Q2.26) to show that the group speed may be

written as

-^-\

U+S&&W*

28k 1

~ dk~ 2

l+8

sinh2<$A;r

where c

is the phase speed. Then for long waves (8k -> 0) we see that

~ c

: the phase and group speeds are the same. On the other hand, for

short waves (8k -> oo), we see immediately that c

~ 3c

/2: the group

speed is greater than the phase speed. For the case of gravity waves only

(so that W

= 0) we have

Wave propagation

for

arbitrary

depth and

wavelength

= -c

(l + 2<5A;cosech2<$A;),

and hence \ < c

< 1; on the other hand, for infinitely deep water with

surface tension (see Q2.27) we obtain

"A.

that is, \ < c

< \ (where equality occurs when W

= 0). These few

observations are sufficient to explain, for example, the phenomenon

represented earlier in Figure 2.2. Waves produced by a fixed disturbance

in a moving stream can be stationary (provided that the speed of the

stream is greater than the minimum speed of propagation of waves).

The energy in the gravity component (the left-hand branch in Figure

2.1) is always propagated at a speed

less

than c

, so these gravity waves

appear behind the disturbance. The capillary

waves,

however, always have

a group speed which is greater than c

, and consequently the forward

propagation of energy for this mode generates these waves

ahead

of the

disturbance. (It turns out that the attenuation of gravity waves is much

less than that for capillary waves - mainly because of their significantly

different wavelengths; see Chapter

- so gravity waves are seen to extend

much further behind the disturbance than capillary waves are seen ahead.)

2.1.3

Concentric waves on deep

water

In Section 2.1 we mentioned some results that can be obtained for wave

propagation, which is governed by the classical wave equation written in

cylindrical coordinates. It is now our intention to describe the character

of purely concentric gravity waves (initiated by a central disturbance) as

they propagate over deep water. Of course, corresponding calculations

are possible for any depth and with surface tension included, but it is

sufficient, both to give a flavour of the results and also for our future

work, to examine this one example. We start with the representation of

the solution obtained from Q2.19:

i) =

j ^j

(2.30)

which satisfies

rj(r,

0) =f(r) (with transform/(/?)) and

(r,

0) = 0. It is

immediately evident that any useful description of the wave profile, rj,

based on the solution (2.30), requires some approach that will produce a

76 2 Some classical problems in water-wave theory

simplification. To this end we choose to analyse the solution in the

regions where t

/r -> oo, a choice that will look reasonable when we

recast the problem so that we may invoke the method of stationary phase.

First, we express the Bessel function, Jo(pr), in the familiar integral

form

7T/2

2 f

(pr)

= - I cos(prcosO)dO, (2.31)

and then write (2.30) as

7t/2

+pr

cos

0 0

f / fc \

(2.32)

where 0t denotes the real part of the double integral. To proceed, we

introduce a new integration variable (q) and a parameter (<r) defined by

q =—p and a = —, (2.33)

respectively. The expression for the surface wave given in equation (2.32)

may therefore be rewritten as

JT/2

Tto-r

o o

+ exp{ia(# - q

cos

6)}]dOdq,

(2.34)

and we examine this by employing Kelvin's method of stationary phase to

give the asymptotic behaviour of

rj(r,

t) as a -> oo (that is, as

/8r

-> oo).

This very powerful and widely used result states (see Q2.16) that

Wave propagation

for

arbitrary

depth and

wavelength

as o -» +00, where the point of

stationary phase

is defined by

«'(0 = 0;

the primes here denote derivatives with respect to Q, and sgn is the

signum function (taking the values +1 or —1). Essentially the idea is

that, for large cr, the integrand oscillates least rapidly near the point

(or, perhaps, points) where oi\q) = 0, and so this is where the dominant

contribution will arise; elsewhere, rapid oscillations approximately can-

cel,

although we might obtain a contribution from the end-points of the

range since symmetry about these points is lost. The error in the beha-

viour given in (2.35) is

O(cr~

in general, as a -> 00. This result is closely

related to the

method

steepest

descent,

and some standard references to

these types of asymptotic evaluation are given in the section on Further

Reading at the end of this chapter. We now apply (2.35) to the double

integral (2.34), once in q and once in 0, and to both exponential terms.

First, in q, the points of stationary phase occur where

1 -\-2q cos 0 =

—2q cos 0 = 0,

which correspond, respectively, to the two exponental terms. However,

since

0 < q < 00 and 0 < 0 < n/2,

the dominant contribution will come only from the second term in the

integral; that is, at

2 cos

The second derivative of the exponent, with respect to q, is then -2

cos

Thus we have

exp{i(-7r + a I

cos

0)/4}d0

cos 0

which itself possesses a point of stationary phase where

sin0 =

or 0 = 0,

and so q = \. Since 0 = 0 occurs at the end of

the

range of integration, the

method of stationary phase produces half

the

contribution represented in

(2.35) (which there uses equal contributions from either side of q = Q).

78 2 Some

classical problems

in water-wave theory

The second derivative of the exponent, evaluated at 0 = 0, takes the value

\ and so

which is the asymptotic behaviour as

/8r

-+ oo. How can we make use

of this result?

Clearly, since the argument of the function / involves P'/r

, and

/8r

-> oo, we require to know the behaviour of/ in order to describe

rj(r,

t). We consider the simple - and idealised - choice of initial

disturbance given by

» 0 < r < a

where

is a constant; this describes a 'top-hat' profile which is used here

to generate the outward propagating concentric wave. The transform of

this function is

a pa

f{p)

AJ rJ

(pr)dr

=^J

(y)dy

where a standard identity between the /

and J

Bessel functions:

has been employed. Thus equation (2.36) becomes

and we choose to interpret the limiting process

/8r

-> oo as t -> oo at

fixed r (and fixed 8).

Then, upon the use of the asymptotic behaviour

IJ ( 3 \

/—cos[y--7t)

I ivy

Wave propagation

for

arbitrary

depth and

wavelength

we find that

00.

This describes, for example at

fixed

r, a wave whose amplitude decays like

\/t and for which the frequency increases; the general character of the

wave is evident in Figure 2.3. This figure clearly demonstrates what is

usually observed for cylindrical gravity waves: the wavelength decreases

at any fixed radius or, equivalently, the wavelength increases outwards

from the centre of the disturbance.

We have, thus far, presented only a rather brief introduction to the

many elementary calculations that are possible in simple water-wave

theory. As we mentioned earlier, other examples (such as waves on mov-

ing streams, standing waves and crossing waves) are explored in the

exercises at the end of this chapter. We also take the opportunity there

to expand on some of the results already discussed, and to describe

alternative approaches to some of

the

standard problems. We now devote

the rest of this section of the chapter to the study of a few slightly less

routine calculations, but ones that begin to demonstrate the breadth and

depth of what can be done even in the linear approximation.

Furthermore, much of this will provide an excellent preparation for

our work on the various nonlinear problems that we shall describe later.

Figure 2.3. A representation of an outward propagating cylindrical (or

concentric) gravity wave.

80 2 Some

classical problems

in water-wave theory

2.2

Wave propagation over variable depth

It is a matter of everyday experience that most water waves do not

propagate over constant depth, whether they be in a man-made reservoir,

a river, or the ocean. Therefore a useful extension to our studies is to

examine the effects of incorporating variable depth. We start with the

most straightforward problem of this type: a plane wave propagating in

the ^-direction, with a depth which also varies only in x (so that

b = b(x)). From equations (2.1) we therefore obtain

with

— r\

and p —

—

Wrj

on z = 1,

and

w = ub'(x) on z = b(x).

In order to make the problem even more manageable, we simplify further

by considering only long waves, so 8 -> 0, and then we are left with

= —p

, p

= 0, u

+ w

= 0,

with

w = rj

, and p =

onz=l, \ (2.37)

and

w = ub'(x) on z = b(x).

These equations immediately yield

i ^ ^

-I

and so

-f rj

= 0

with

w = (1

—

z)u

+ r\

since u is not a function of z (in this approximation). Finally, evaluating

w on z = ft, we obtain the pair of equations

(>,

(2.38)

where d(x) =

- b(x) is the local depth. These equations, (2.38), are

usually called the linearised shallow water equations and, upon the

elimination of

they give

ritt-(dri

)

(2.39)

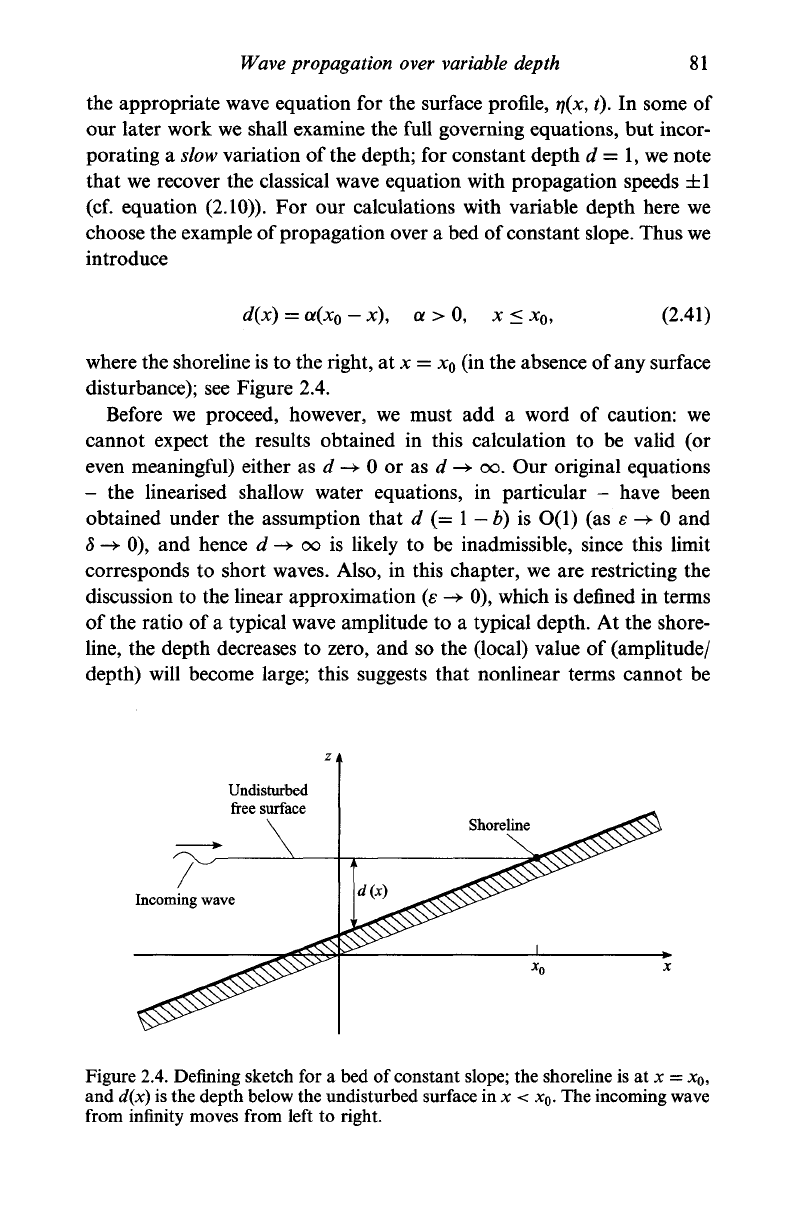
Wave propagation over variable depth

the appropriate wave equation for the surface profile,

rj(x,

t). In some of

our later work we shall examine the full governing equations, but incor-

porating a

slow

variation of the depth; for constant depth d = 1, we note

that we recover the classical wave equation with propagation speeds ±1

(cf. equation (2.10)). For our calculations with variable depth here we

choose the example of propagation over a bed of constant slope. Thus we

introduce

d(x) = a(x

-x), a > 0, x < x

, (2.41)

where the shoreline is to the right, at x = x

(in the absence of any surface

disturbance); see Figure 2.4.

Before we proceed, however, we must add a word of caution: we

cannot expect the results obtained in this calculation to be valid (or

even meaningful) either as d -» 0 or as d

oo. Our original equations

- the linearised shallow water equations, in particular - have been

obtained under the assumption that d (=

1 —

b) is O(l) (as s -> 0 and

8 -> 0), and hence d -* oo is likely to be inadmissible, since this limit

corresponds to short waves. Also, in this chapter, we are restricting the

discussion to the linear approximation (e -> 0), which is defined in terms

of the ratio of a typical wave amplitude to a typical depth. At the shore-

line,

the depth decreases to zero, and so the (local) value of (amplitude/

depth) will become large; this suggests that nonlinear terms cannot be

Undisturbed

free surface

Incoming wave

Shoreline ^-<<^^^

d(x)

^gf^S^^

Figure 2.4. Defining sketch for a bed of constant slope; the shoreline is at x = x

and d(x) is the depth below the undisturbed surface in x < x

. The incoming wave

from infinity moves from left to right.

82 2 Some

classical problems

in water-wave theory

ignored as d -> 0. With these provisos in mind, let us proceed with the

analysis.

The wave equation for

rj(x,

t), (2.40), with d(x) given by (2.41),

becomes

- a(x

x)rj

arj

= 0, (2.42)

and we seek a solution which is harmonic in /:

iOt

+ c.c., (2.43)

where

is a real constant (the frequency) and A(x) is an amplitude

function (which, in general, is complex). (As we have mentioned before,

this type of solution can be used as the basis for more general solutions

by introducing, for example, the Fourier transform.) Equation (2.42)

therefore yields the differential equation for A(x),

a(x

- x)A" - aA' +

= 0,

which shows that we may take A(x) to be real (but see below). It is

convenient to treat A as a function of x

- x = X, say, so that

for A(X), which we recognise is related to the Bessel equation. To confirm

this,

we now regard iasa function of

2coJ—

= x,

and so we obtain

' + x^ = 0, (2.44)

where A = A(x) = A(2co^(x

x)/a).

We observe that the shoreline is at

X = 0 (so x = 0 there) and that the undisturbed water exists in X > 0.

Equation (2.44) is the Bessel equation of zero order, and we now require

the appropriate solution in x > 0.

The general solution for A(x) is

where C and D are arbitrary (complex) constants. This solution contains

a contribution (/

) which is regular at the shoreline (x = x

; that is,

= 0) since Jo(x), as a power series, contains only even powers of x

(so only integer powers of (x

—

x) appear). On the other hand, the

second part of the solution (F

) gives rise to a logarithmic singularity

at x = 0, so we might expect that we should assign D = 0; we shall,

Wave propagation

over

variable

depth 83

however, retain this term for the present. The solution of our original

equation, (2.42), therefore becomes

r)(x,

t) = I CJ

(

2coJ—

2co

/— J

\e~

1(Ot

+ c.c, (2.45)

and a natural next move is to examine the detailed character of this

solution far away from the shore (x

—

oo) and close to the shoreline

at x =

(We observe that, in equation (2.45), it is quite acceptable to

choose both C and D to be real, as we mentioned earlier.)

First, for large values of the argument x? we use the standard results

(/<>,

Yo)

~ J—(cos(x - TT/4), sin(x - TT/4)) as x -> +oo,

and thus equation (2.45) yields

•

rt ~

as x

—

-»•

+oo. This is usefully rewritten in the form

Z>)exp

-i( 2ay^_Jl +

^ -

(

)

which describes two wave components, one moving to the right and one

to the left. The first exponential term (with the coefficient C + D) is a

right-going wave; it is therefore the plane wave which is approaching the

shoreline (see Figure 2.4). The second exponential term represents the

left-going component, and this is therefore a wave which is reflected from

the shoreline. In both components we observe that the speed of propaga-

tion is not constant. The speed can be determined by considering the lines

of constant phase, defined by

— X ,

cot

= constant.

Along these lines we have

±M*ox)

±Vd(xJl

(2-47)