Johnson R.S. A Modern Introduction to the Mathematical Theory of Water Waves

Подождите немного. Документ загружается.

Some

classical problems

water-wave

theory

Also,

equations

(2.6)

show that

and hence

the

boundary condition

on P (in

(2.7)) gives

)^(>0);

(2.9)

this

is the

dispersion relation

for

(plane) surface waves

and so

determines

a>(k)

(and

hence

the

phase speed c

(k)).

Thus

for

waves

of any

wave number,

k, and

with

the

surface tension

contribution included,

we can

find

the

speed,

, of

these waves.

(We

observe that

(2.9) is an

expression

for

so it is

possible

have propa-

gation both

to the

right {c

> 0) and to the

left

< 0), as we

would

expect.)

The

dispersion relation

is a

function

= h

/A,

where

= X/k is the

(physical) wavelength

of the

wave initiated

at t = 0. We

may

now

examine

the

special cases

-> 0 and

-> oo.

The first case,

8k -> 0,

which describes long waves

(or

shallow water),

gives rise

to the

very simple result

<£

(2.10)

which,

original physical variables, produces

the

speeds

propagation

,~±v^, (2.11)

which

independent

of the

wave number,

and so

these waves

are

non-

dispersive.

(This speed of propagation,

y/gh^,

confirms the choice of scales

adopted

Section

1.3.1.)

The speeds given

(2.10)

are

also independent

the

Weber number,

but

directly related

to g, so

waves that travel

these speeds

are

called

gravity waves

(see (2.11)). Indeed,

the

gravity wave

describes

oscillatory balance between kinetic

and

potential energy,

the gravitational field.

the

other hand

the

limit 8k

oo,

which describes short waves

(or

deep water), yields

~8kW

(2.12)

and waves moving

at the

speeds obtained from (2.12)

are

called

capillary waves

(or,

sometimes,

ripples).

comment that

our

preferred

Wave propagation

for

arbitrary

depth and

wavelength

terminology is to emphasize the wavelength of the wave rather than the

depth of the water (provided that this depth remains finite); we therefore

discuss long

waves

or short

waves

as the limiting forms.

Now, if we consider an environment for which it is reasonable to

ignore the effects of surface tension altogether (that is, W

is always

negligibly small), equation (2.9) becomes

4 =

tanh

8k '

(2.13)

for gravity waves of any wavelength. Then for short waves, where

8k -> oo, we obtain

(or ±

in dimensional variables);

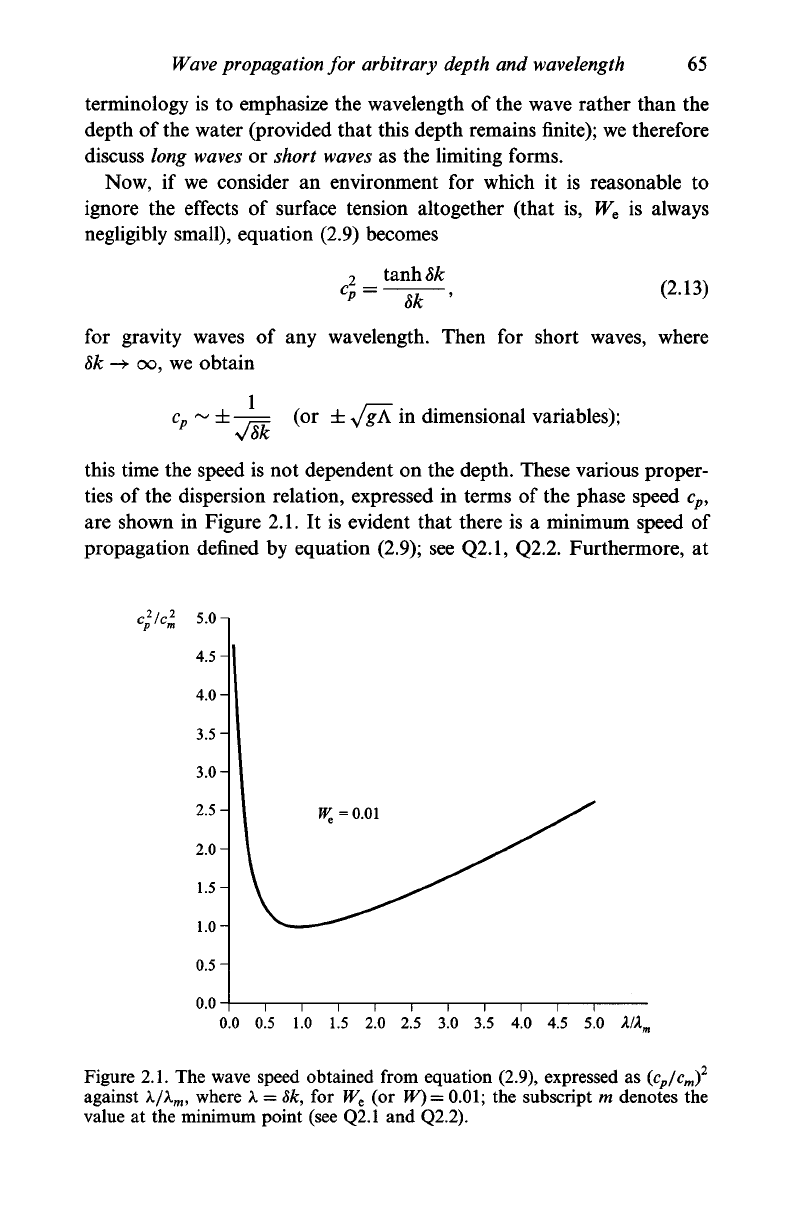
this time the speed is not dependent on the depth. These various proper-

ties of the dispersion relation, expressed in terms of the phase speed c

are shown in Figure 2.1. It is evident that there is a minimum speed of

propagation defined by equation (2.9); see Q2.1, Q2.2. Furthermore, at

0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 M

Figure 2.1. The wave speed obtained from equation (2.9), expressed as (c

)

against k/k

, where k =

8k,

for W

(or W)=

0.01;

the subscript m denotes the

value at the minimum point (see Q2.1 and Q2.2).

66 2 Some classical problems in water-wave theory

any given speed above this minimum, two waves - a gravity wave and a

capillary wave - can coexist at the same speed. This is sometimes

observed when capillary waves are seen 'riding on' gravity waves, both

moving at essentially the same speed. However, a more dramatic phe-

nomenon occurs if a disturbance is generated in a moving stream.

Provided that the stream is moving faster than the minimum propagation

speed, two sets of standing (stationary) waves can often be observed: one

of rather long waves (gravity waves) behind the disturbance, the other of

rather short waves (capillary waves)

ahead

of the disturbance; see Figure

2.2.

(That some waves can propagate forward of the disturbance is, per-

haps,

rather surprising; this will be explained in due course.) The inclu-

sion of a stream moving at a constant speed (for all x and z) is described

inQ2.11.

Corresponding calculations are also possible in cylindrical geometry

(and based, therefore, on equations (2.2)). One of the simplest cases arises

for long waves (<5-^ 0) with b = 0; see Q2.17. The surface wave is

then described by the classical wave equation, written in cylindrical

coordinates

In ~

(rirr

+ \

= 0. (2.14)

This equation can be solved by using the conventional method of separa-

tion of variables, perhaps coupled with the use of an integral transform;

see Q2.18 and Q2.19. Indeed, if

seek a solution for purely concentric

waves,

rj(r,

t), and make use of the Hankel

transform

yip) = / ry(r)J

(pr)dr (p > 0),

Flow direction

•

Object

Capillary waves / Gravity waves

Figure 2.2. Schematic representation of the generation of capillary waves and

gravity waves by a fixed object in the surface of a moving stream.

Wave

propagation

for

arbitrary depth and

wavelength

then

the

Hankel transform

rj(r,

(written

fj(t;

p)) satisfies

f)»+p

see Q2.18. (This result does require

the

introduction

appropriate

boundedness

and

decay conditions.) Then given,

at t =

0, that

=f(r) and

= 0,

we obtain

fj=f(p)cospt,

where f(p)

the transform of/(r); thus, using the inverse transform,

obtain

t)=

pf{p) cos (tp)J

(rp)dp.

This type

solution, suitably adjusted

for

deep water (see Q2.19), will

provide the basis

for a

brief description

the propagation

concentric

waves

Section

2.1.3.

(We comment that some authors prefer

use

the

symmetric version

the Hankel transform:

yip)

f(pr)

l/2

y(r)Jo(pr)dr.)

2.1.1 Particle paths

An important consideration

any wave motion

is to

find what,

any-

thing,

actually moved (presumably

the direction

propagation)

the wave progresses. This might involve,

for

example, mass

momen-

tum or energy. In water waves,

first calculation of this type is to find

the

particle paths that describe the motion of the fluid particles on and below

the surface. Then,

for

example, any motion that occurs near the bottom

of the flow will provide the necessary source

for

the displacement

the

sediment

(if

the

bed of

the flow

is so

comprised).

In our simple linear calculation, we have so

far

determined the vertical

velocity component, from (2.8),

and the

horizontal velocity component

(in Q2.3); these

are

sinh Skz

cosh Skz

w= -icoA

. E

+ c.c;

u =

8coA

is+cc.,

sinh<5A:

sinh^A:

68 2 Some classical problems in water-wave theory

respectively, where E = exp{i(fcc

—

cot)}.

The particle paths are then

defined by

dx dz

- = su, - =

£W

, (2.15)

and note the inclusion of the parameter e, required since the particle

paths are, in general,

— = u and u = s(w, w) here.

Thus equations (2.15) describe paths whose amplitude is O(e); it is

therefore convenient to introduce

x = x

+ eX, Z =

+ eZ,

where x

and z

are treated as fixed (and O(l)). The particle paths as

s -> 0 - the approximation used throughout this work on linear waves -

are now described by

cosh 8kz

^ dZ .

sinh 8kz

8coA .

^Q + c.c; icoA . .

£Q +

dt sinh^A: dt smhSk

where E

= exp{i(foc

—

^0)- These may be integrated directly to give

cosh

8kzo

sinh

Skzn

„

X - iSA . °£

+ c.c, Z ~A .

°Eo + c.c,

sinh5A: sinh<5/:

where the arbitrary constant is set to zero in each case (so that X = 0 and

Z = 0 when ^4 = 0). This representation of the particle paths is usefully

recast as

/ X \

/ Z \

_ A\A\

\S cosh Skz

) \sinh5A:zo/ (sinh^

, 0<z

<l, (2.16)

sinh

8k)'

to leading order as e -> 0.

The fluid particles, in the neighbourhood of the point (x

, z

), move on

ellipses for which

major axis , ,

—r^ = 8coth8kz

minor axis

(and which collapse to a point when A = 0, as one would expect). For

long waves, 5^0, the major and minor axes become, respectively,

4\A\/k and

4\A\z

Wave propagation

for

arbitrary

depth and

wavelength

which describe different ellipses at different depths, and which approach

the (degenerate) horizontal path as z

-> 0. On the other hand, for short

waves

-> oo), the corresponding results are

48\A\Q-

8k{l

Zo)

and 4|^|e-^

Zo)

whose ratio does not vary as z

varies. In this case the ellipses are all of

the same eccentricity, but of decreasing size as z

decreases. (Indeed, in

original physical variables, these trajectories become

circles

of decreasing

radius as z

decreases; see Q2.4.)

We have found, therefore, that (in this first approximation) as the

small-amplitude wave propagates on the surface, the

fluid

particles follow

closed paths. Consequently there is no net transfer of material particles

due to the passage of the wave (at least, at this order of approximation).

In particular, near the bottom of the flow there is, predominantly, a

horizontal

oscillatory

motion of

the

fluid as a long wave propagates over-

head. Clearly, there is (at this order) no net flow of matter, but what of

energy, for example?

2.1.2 Group velocity and the propagation of energy

We return to our first analysis in which we examined the solution

initiated by a pure harmonic wave of fixed amplitude. This time, how-

ever, we construct the solution to equations (2.3) with the initial surface

profile now given by

= A(ax)Q

lkx

+ c.c,

where A is a complex-valued function. For a -> 0, this describes (with k

fixed) another pure harmonic wave, but here with a slowly varying ampli-

tude;

this is obviously an improvement on our simplest case. (Another

generalisation is to allow for many - perhaps all - wave numbers, k; this

choice is discussed in Q2.22.) The purpose is to obtain the appropriate

solution of equations (2.3) which is uniformly valid as a -> 0; see Section

1.4.2.

The parameter, 8, is held fixed and, for simplicity, we consider

only gravity waves (so the Weber number, W

, is set to zero); the

corresponding calculation for

^ 0 is described in Q2.26.

As before, it is convenient to introduce

E = Qxp{i(kx -

cot)},

70 2 Some

classical problems

water-wave

theory

and then we seek a solution which also depends on the slow scales

X = ax, T = at. (2.17)

The inclusion of T is a reasonable manoeuvre, since the solution is to be a

wave that propagates in x and t, and the slow space scale (X = ax, given

in the initial datum) is therefore likely to have an associated slow time

scale; of

course,

we lose nothing by including it (see also Q1.54). We seek

a solution in the form

u = U(z, X, T;

ot)E,

w = W(z, X, T; a)E, p = P(z, X, T; ci)E,

with

tl =

A(X,T;a)E

plus the complex conjugate in each case. The equations (2.3) yield

icoU

- aU

= ikP + aP

;

(icoW

- aW

) = P

; 1

(

with

W(\, X, T\ a) = -icoA

;

Z>(1,

X, T; a) = A; W(0, X, T, a) = 0.

(2.19)

If an appropriate solution of these equations exists (at least, as a -> 0),

then uniform validity as \kx

—

a)t\^oo is guaranteed since the complete

solution has been constructed with only E

(but then E~

as well)

included: no higher harmonics and secular terms can be generated (cf.

equation (1.106) et

seq.).

Directly from equations (2.18) we see that

and the relevant solution here satisfies

thus we obtain

( ^\ W = 0. (2.20)

Wave propagation

for

arbitrary depth

and

wavelength

An asymptotic solution

of the

system (2.18)

and

(2.19)

sought

in the

form

(2.21)

where

Q=U, W, P, or A (and

correspondingly

for Q

Hence, with

(2.21) used

(2.20),-we obtain

the

equations

Ozz

- 8

= 0;

lzz

- 8

-2\k8

(2.22)

and

so on.

From

our

previous calculation (Section

2.1), we

have

immediately that

where

(co/k)

(tanh 8k)/(8k);

see

equations

(2.8) and

(2.13).

Now,

for

W\, we

obtain

(2.24)

Mini

o/c j

which

has the

solution,

for

arbitrary

(X, T),

= B

sinh

8kz -

8coA

———-^, (2.25)

l ox

sinh<5fc

which satisfies

{$, X, T) = 0. The

other

two

boundary conditions

this order

(see

(2.19))

are

-icoA

+ A

and P

= A

on z = 1.

(2.26)

The first

these yields

ia)A

+ A

= B

sinh8k

8coA

coth8k, (2.27)

and

the

second uses (from equations (2.18))

ikP

+ P

icoU

- U

and ikU

+ U

+ W

= 0 on z = 1.

Q2.3 we are led to the

results

8co

/cosh

8kz\

/cosh

8kz\

—

j and UQ =

SCOAQ

—

and

ikP

+-^rA

coth8k

-8co(jA

+ A

coth8k

- j W

72 2 Some classical problems in water-wave theory

on z = 1. Hence from (2.25) and (2.26) we obtain

^ A

+ A

\ coth<5A; = -

8coB

+ -T-

^0*

(** + coth 8k) (2.28)

and upon the elimination of B\ between equations (2.27) and (2.28) we

finally have

+ wz

+ «£(coth

5A:

- tanh Sfc)M

jr = 0. (2.29)

We have derived the equation which describes the variation of the

leading-order approximation to the amplitude, A

; this equation does

not involve A

because this is eliminated with B

when o)(k) is used.

The general solution of (2.29) is

F(X-c

T),

where F is determined by the initial datum (on T = 0) and

= ^-

+ <5£(coth 8k - tanh 8k)}.

It is left as an exercise to confirm that this speed of propagation is indeed

the group speed:

= -— where <y =-tanh<$fc.

In another context, we provide curves of c

and c

(for gravity waves) as

functions of 8k; see Figure 4.1.

Thus,

although the individual waves move forward at the phase speed

co/k),

the envelope or group moves at the group speed, c

. Indeed,

this general property of a wave is easily explained by a simple (but heur-

istic) argument involving two waves of the same amplitude but differing

slightly in wave number; see Q2.28. (The reason for our rather lengthier

approach, apart from presenting a more careful treatment, is to introduce

the techniques that we shall require later. A neater approach, which

avoids finding A\, is described in Q2.30.) The inclusion of the surface

tension leads to the corresponding result, but with c

now the appropriate

group speed deduced from the dispersion relation (2.9); see Q2.26.

The connection between the propagation of the group and the propa-

gation of energy is now easily stated. It is a familiar result that the energy

in a wave motion is proportional to the square of the amplitude of the

wave; here, this implies that the energy is proportional to

But we

Wave propagation

for

arbitrary

depth and

wavelength

have just demonstrated that A

is a function of (X - c

T), and so the

energy propagates at the group speed. There are many ways of presenting

this argument in a more precise form, some of which are rehearsed in the

exercises; here we describe one such method that uses the general notion

of energy, as developed in Section

1.2.5.

From equation (1.48), we have

that the total energy (per unit horizontal area) in the flow is

written in physical variables. This is re-expressed using our

nondimensional and scaled variables (described in Section 1.3) as

where $ -> pgh\S describes the nondimensionalisation of S. For our

simple problem of one-dimensional wave propagation (with b = 0), this

becomes

l+er}

where u and w are given by U

and W

, respectively, to leading order as

a-> 0.

Our primary concern here is with the energy carried by, let us say, one

period of the wave. Thus we first introduce

u - U

E + UQET

, W - W

E + W

E~\

where E = exp(iA;§), $ = x

—

t and the overbar denotes the complex

conjugate, and then we define the energy carried by just one period of

the wave: this is

2n/k

Consistent with the linearisation (s -> 0) that we have so far adopted, we

therefore obtain