Jeevanjee N. An Introduction to Tensors and Group Theory for Physicists

Подождите немного. Документ загружается.

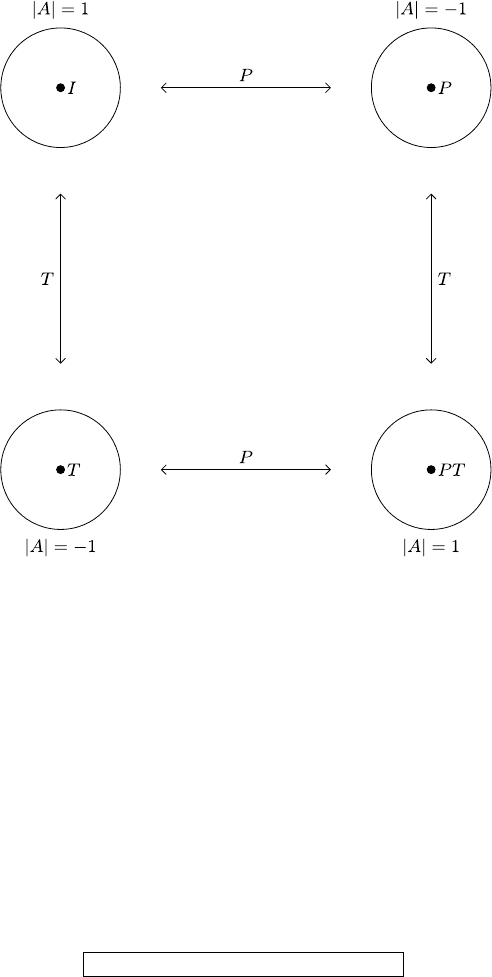
4.3 Homomorphism and Isomorphism 103

Fig. 4.2 The four components of O(3, 1). The proper Lorentz transformations in the upper-left

corner are just SO(3, 1)

. Note that the transformations in the lower-right hand corner change both

the orientation of the space axes as well as time, and so must be disconnected from SO(3, 1)

even

though they have |A|=1. Also note that multiplying by the parity and time-reversal operators P

and T take one back and forth between the various components

4.3 Homomorphism and Isomorphism

In the last section we claimed that there is a close relationship between SU(2) and

SO(3), as well as between SL(2, C) and SO(3, 1)

. We now make this relationship

precise, and show that a similar relationship exists between S

and Z

. We will also

deﬁne what it means for two groups to be ‘the same’, which will then tie into our

somewhat abstract discussion of Z

in the last section.

Given two groups G and H ,ahomomorphism from G to H is a map  :G →H

such that

(g

) =(g

)(g

) ∀g

∈G. (4.36)

Note that the product in the left hand side of (4.36) takes place in G, whereas the

product on the right hand side takes place in H . A homomorphism should be thought

of as a map from one group to another which preserves the multiplicative structure.

Note that  need not be one-to-one or onto; if it is onto then  is said to be a

104 4 Groups, Lie Groups, and Lie Algebras

homomorphism onto H , and if in addition it is one-to-one then we say  is an

isomorphism.If is an isomorphism then it is invertible and thus sets up a one-to-

one correspondence which preserves the group structure, so we regard G and H as

‘the same’ group, just with different labels for the elements. When two groups G

and H are isomorphic we write G H .

Exercise 4.12 Let  : G → H be a homomorphism, and let e be the identity in G and e



the identity in H . Show that

(e) =e







−1



=(g)

−1

∀g ∈G.

Example 4.17 Isometries and the orthogonal, unitary, and Lorentz groups

A nice example of a group isomorphism is when we have an n-dimensional vector

space V (over some scalars C) and a basis B, hence a map

GL(V ) →GL(n, C)

T →[T ]

It is easily checked that this map is one-to-one and onto. Furthermore, it is a homo-

morphism since [TU]=[T ][U], a fact you proved in Exercise 2.8. Thus this map is

an isomorphism and GL(V ) GL(n, C).IfV has a non-degenerate Hermitian form

(·|·) then we can restrict this map to Isom(V ) ⊂GL(V ), which yields

Isom(V ) O(n)

when V is real and (·|·) is positive-deﬁnite,

Isom(V ) U(n)

when V is complex and (·|·) is positive-deﬁnite, and

Isom(V ) O(n −1, 1)

when V is real and (·|·) is a Minkoswki metric. These isomorphisms were implicit

in the discussion of Examples 4.3–4.6, where we identiﬁed the operators in Isom(V )

with their matrix representations in the corresponding matrix group. 

Example 4.18 Linear maps as homomorphisms

A linear map from a vector space V to a vector space W is a map  :V →W that

satisﬁes the usual linearity condition

(cv

) =c(v

) +(v

). (4.37)

(A linear operator is then just the special case in which V = W .) In particular we

have (v

+ v

) = (v

) + (v

), which just says that  is a homomorphism

between the additive groups V and W ! (cf. Example 4.2). If  is one-to-one and

4.3 Homomorphism and Isomorphism 105

onto then it is an isomorphism, and in particular we refer to it as a vector space

isomorphism.

The notions of linear map and vector space isomorphism are basic ones, and

could have been introduced much earlier (as they are in standard linear algebra

texts). Because of our speciﬁc goals in this book, however, we have not needed them

yet. These objects will start to play a role soon, though, and will recur throughout

the rest of the book.

Exercise 4.13 Use an argument similar to that of Exercise 2.6 to prove that a linear map

φ :V → W is an isomorphism if and only if dim V =dim W and φ satisﬁes

φ(v) =0 ⇒ v =0.

Exercise 4.14 Before moving on to more complicated examples, let us get some practice

by acquainting ourselves with a few more basic homomorphisms. First, show that the map

exp :R →R

∗

x →e

from the additive group of real numbers to the multiplicative group of nonzero real num-

bers, is a homomorphism. Is it an isomorphism? Why or why not? Repeat the analysis for

exp :C →C

∗

. Also, show that the map

det :GL(n, C) → C

∗

A →det A

is a homomorphism for both C =R and C =C. Is it an isomorphism in either case? Would

you expect it to be?

Exercise 4.15 Recall that U(1) is the group of 1×1 unitary matrices. Show that this is just

the set of complex numbers z with |z|=1, and that U(1) is isomorphic to SO(2).

Suppose  is a homomorphism but not one-to-one. Is there a way to quantify

how far it is from being one-to-one? Deﬁne the kernel of  to be the set K ≡

{g ∈G |(g) =e



}, where e



is the identity in H. In other words, K is the set of all

elements of G that get sent to e



under .If is one-to-one, then K ={e}, since

there can be only one element in G that maps to e



and by Exercise 4.12 that is e.If

 is not one-to-one, then the size of K tells us how far it is from being so. Also, if

we have (g

) =(g

) =h ∈H , then





−1



=(g

)(g

)

−1

=hh

−1

so g

−1

is in the kernel of ,i.e.g

−1

= k ∈ K. Multiplying this on the right

by g

then gives g

= kg

, so we see that any two elements of G that give the

same element of H under  are related by left multiplication by an element of K.

Conversely, if we are given g ∈G and (g) =h, then for all k ∈K,

(kg) =(k)(g) =e



(g) =(g) =h.

Thus if we deﬁne Kg ≡{kg | k ∈ K}, then Kg are precisely those elements (no

more, and no less) of G which get sent to h. Thus the size of K tells us how far 

106 4 Groups, Lie Groups, and Lie Algebras

is from being one-to-one, and the elements of K tell us exactly which elements of

G will map to a speciﬁc element h ∈H .

Homomorphisms and isomorphisms are ubiquitous in mathematics and occur

frequently in physics, as we will see in the examples below.

Exercise 4.16 Show that the kernel K of any homomorphism  : G → H is a subgroup

of G. Then determine the kernels of the maps exp and det of Exercise 4.14.

Exercise 4.17 Suppose  :V →W is a linear map between vector spaces, hence a homo-

morphism between abelian groups. Conclude from the previous exercise that the kernel K

of  is a subspace of V , also known as the null space of . The dimension of K is known

as the nullity of K . Also show that the range of  is a subspace of W , whose dimension is

known as the rank of . Finally, prove the rank-nullity theorem of linear algebra, which

states that

rank() +nullity() =dimV. (4.38)

(Hint: Take a basis {e

,...,e

} for K and complete it to a basis {e

,...,e

} for V ,where

n =dim V . Then show that {(e

k+1

), . . . , (e

)} is a basis for the range of .)

Example 4.19 SU(2) and SO(3)

In most physics textbooks the relationship between SO(3) and SU(2) is described

in terms of the ‘inﬁnitesimal generators’ of these groups. We will discuss inﬁnitesi-

mal transformations in the next section and make contact with the standard physics

presentation then; here we present the relationship in terms of a group homomor-

phism ρ : SU(2) → SO(3), deﬁned as follows: consider the vector space (check!)

of all 2 ×2 traceless anti-Hermitian matrices, denoted as su(2) (for reasons we will

explain later). You can check that an arbitrary element X ∈su(2) can be written as

X =



−iz −y −ix

y −ix iz



, x,y,z∈R. (4.39)

If we take as basis vectors

≡−



0 −i

−i 0



≡−



0 −1



≡−



−i 0

0 i



then we have

X =xS

+yS

+zS

so the column vector corresponding to X in the basis B ={S

} is

4.3 Homomorphism and Isomorphism 107

[X]=

⎛

⎝

⎞

⎠

Note that

detX =







[X]



so the determinant of X ∈ su(2) is proportional to the norm squared of [X]∈R

with the usual Euclidean metric. Now, you will check below that A ∈SU(2) acts on

X ∈su(2) by the map X →AXA

†

, and that this map is linear. Thus, this map is a

linear operator on su(2), and can be represented in the basis B by a 3 ×3matrix

which we will call ρ(A), so that [AXA

†

]=ρ(A)[X] where ρ(A) acts on [X] by

the usual matrix multiplication. Furthermore,



ρ(A)[X]





AXA

†





=4det



AXA

†



=4det X =



[X]



(4.40)

so ρ(A) preserves the norm of X. This implies (see Exercise 4.19 below) that

ρ(A) ∈ O(3), and one can in fact show

that detρ(A) =1, so that ρ(A) ∈ SO(3).

Thus we may construct a map

ρ :SU(2) →SO(3)

A →ρ(A).

Furthermore, ρ is a homomorphism, since

ρ(AB)[X]=



(AB)X(AB)

†





ABXB

†



=ρ(A)



BXB

†



=ρ(A)ρ(B)[X] (4.41)

and hence ρ(AB) = ρ(A)ρ(B).Isρ an isomorphism? One can show

that ρ is

onto but not one-to-one, and in fact has kernel K ={I,−I }. From the discussion

preceding this example, we then know that ρ(A) = ρ(−A) ∀A ∈ SU(2) (this fact

is also clear from the deﬁnition of ρ), so for every rotation R ∈SO(3) there corre-

spond exactly two matrices in SU(2) which map to R under ρ. Thus, when trying

to implement a rotation R on a spin 1/2 particle we have two choices for the SU(2)

matrix we use, and it is sometimes said that the map ρ

−1

from SO(3) to SU(2) is

double-valued. In mathematical terms one does not usually speak of functions with

multiple-values, though, so instead we say that SU(2) is the double cover of SO(3),

since the map ρ is onto (‘cover’) and two-to-one (‘double’).

See Problem 4.7 of this chapter, or consider the following rough (but correct) argument:

ρ :SU(2) →O(3) as deﬁned above is a continuous map, and so the composition

det ◦ρ :SU(2) →R

A →det



ρ(A)



is also continuous. Since SU(2) is connected any continuous function must itself vary continuously,

so det ◦ρ cannot jump between 1 and −1, which are its only possible values. Since det(ρ(I )) =1,

we can then conclude that det(ρ(A)) =1 ∀A ∈SU(2).

See Problem 4.7 again.

108 4 Groups, Lie Groups, and Lie Algebras

Exercise 4.18 Let A ∈ SU(2), X ∈ su(2). Show that AXA

†

∈ su(2) and note that

A(X + Y)A

†

= AXA

†

+ AY A

†

, so that the map X → AXA

†

really is a linear operator

on su(2).

Exercise 4.19 Let V be a real vector space with a metric g and let R ∈

L(V ) preserve

norms on V ,i.e.g(Rv,Rv) =g(v,v) ∀v ∈ V . Show that this implies that

g(Rv,Rw) =g(v, w) ∀v,w ∈ V,

i.e. that R is an isometry. Hint: consider g(v +w,v +w) and use the bilinearity of g.

Example 4.20 SL(2, C) and SO(3, 1)

Just as there is a two-to-one homomorphism from SU(2) to SO(3), there is a two-to-

one homomorphism from SL(2, C) to SO(3, 1)

which is deﬁned similarly. Consider

the vector space H

is a four-dimensional vector space with basis B ={σ

,σ

,I}, and an arbitrary

element X ∈H

X =



t +zx−iy

x +iy t −z



=xσ

+yσ

+zσ

+tI (4.42)

so that

[X]=

⎛

⎜

⎝

⎞

⎟

⎠

Now, SL(2, C) acts on H

X →AXA

†

where A ∈SL(2, C). You can again check that this is actually a linear

map from H

which we will again call ρ(A). You can also check that

detX =t

−x

−y

−z

=−η



[X], [X]



so the determinant of X ∈ H

Minkowski metric on R

. As before, the action of ρ(A) on [X] preserves this

norm (by a calculation identical to (4.40)), and you will show in Problem 4.8 that

detρ(A) =1 and ρ(A)

> 1, so ρ(A) ∈SO(3, 1)

. Thus we can again construct a

map

ρ :SL(2, C) →SO(3, 1)

A →ρ(A)

and it can be shown

that ρ is onto. Furthermore, ρ is a homomorphism, by a

calculation identical to (4.41). The kernel of ρ is again K ={I,−I } so SL(2, C) is

a double-cover of SO(3, 1)

See Problem 4.8 again.

4.3 Homomorphism and Isomorphism 109

Exercise 4.20 The elements of SL(2, C) that correspond to rotations should ﬁx timelike

vectors, i.e. leave them unchanged. Identify the elements of H

like vectors, and show that it is precisely the subgroup SU(2) ⊂SL(2, C) which leaves them

unchanged, as expected.

Example 4.21 Z

, parity and time-reversal

Consider the set {I,P}⊂O(3, 1). This is an abelian two-element group with

= I , and so looks just like Z

. In fact, if we deﬁne a map  :{I,P}→Z

(I) =1

(P ) =−1

then  is a homomorphism since

(P ·P)=(I) =1 =(−1)

=(P )(P).

 is also clearly one-to-one and onto, so  is in fact an isomorphism! We could also

consider the two-element group {I,T}∈O(3, 1); since T

= I , we could deﬁne a

similar isomorphism from {I,T } to Z

. Thus,

{I,P}{I,T }.

In fact, you will show below that all two-element groups are isomorphic. That is

why we chose to present Z

somewhat abstractly; there are many groups in physics

that are isomorphic to Z

, so it makes sense to use an abstract formulation so that

we can talk about all of them at the same time without having to think in terms of

a particular representation like {I,P} or {I,T }. We will see the advantage of this in

the next example.

Exercise 4.21 Show that any group G with only two elements e and g must be isomorphic

to Z

. To do this you must deﬁne a map  :G →Z

which is one-to-one, onto, and which

satisﬁes (4.36). Note that S

, the symmetric group on two letters, has only two elements.

What is the element that corresponds to −1 ∈Z

Example 4.22 S

, Z

, and the sgn homomorphism

In Sect. 3.8 we discussed rearrangements, transpositions, and the evenness or odd-

ness of a rearrangement in terms of the number of transpositions needed to obtain

it. We are now in a position to make this much more precise, which will facilitate

neater descriptions of the  tensor, the determinant of a matrix, and the symmetriza-

tion postulate.

We formally deﬁne a transposition in S

to be any permutation σ which switches

two numbers i and j and leaves all the others alone. You can check that σ

and σ

·σ

from Example 4.9 are both transpositions. It is a fact that any permutation can be

written (non-uniquely) as a product of transpositions, though we will not prove this

here.

As a simple example, though, you can check that

See Herstein [9] for a proof and nice discussion.

110 4 Groups, Lie Groups, and Lie Algebras



123

231





123

321



123

213



is a decomposition of σ

into transpositions.

Though the decomposition of a given permutation is far from unique (for in-

stance, the identity can be decomposed as a product of any transposition σ and its

inverse), the evenness or oddness of the number of transpositions in a decomposition

is invariant. For instance, even though we could write the identity as

e =e

e =σ

−1

e =σ

−1

and so on for any transpositions σ

,σ

,..., every decomposition will consist of an

even number of transpositions. Likewise, any decomposition of the transposition



123

213



will consist of an odd number of transpositions. A general proof of this fact

is relegated to Problem 4.9. What this allows us to do, though, is deﬁne a homomor-

phism sgn: S

→Z

sgn(σ ) =



+1ifσ consists of an even number of transpositions

−1ifσ consists of an odd number of transpositions.

You should be able to verify with a moment’s thought that

sgn(σ

) =sgn(σ

) sgn(σ

so that sgn is actually a homomorphism. If sgn(σ ) =+1wesayσ is even, and if

sgn(σ ) =−1wesayσ is odd.

With the sgn homomorphism in hand we can now tidy up several deﬁnitions

from Sect. 3.8. First of all, we can now deﬁne the wedge product of r dual vectors

, i =1,...,r to be

∧···∧f

≡



σ ∈S

sgn(σ )f

σ(1)

⊗f

σ(2)

⊗···⊗f

σ(r)

. (4.43)

You should compare this with the earlier deﬁnition and convince yourself that the

two deﬁnitions are equivalent. Also, from our earlier deﬁnition of the  tensor it

should be clear that the nonzero components of  are



...i

=sgn(σ ) where σ =



1 ··· n

··· i



(4.44)

and so the deﬁnition of the determinant, (3.85), becomes

|A|=



σ ∈S

sgn(σ )A

1σ(1)

...A

nσ (n)

. (4.45)

Finally, at the end of Example 4.9 we described how S

acts on an n-fold tensor

product T

(V ) by

σ(v

⊗v

⊗···⊗v

) =v

σ(1)

⊗v

σ(2)

⊗···⊗v

σ(n)

, (4.46)

4.4 From Lie Groups to Lie Algebras 111

where the action of σ on a generic element on T

(V ) (which would be a sum

of product states like the above) is determined by linearity. If we have a totally

symmetric tensor T =T

...i

⊗···⊗e

∈S

(V ), we then have

σ(T)=T

...i

σ(i

)

⊗···⊗e

σ(i

)

−1

)...σ

−1

)

⊗···⊗e

where we have relabeled indices using j

≡σ(i

)

...j

⊗···⊗e

by total symmetry of T

...j

so all elements of S

(V ) are ﬁxed by the action of S

. If we now consider a totally

antisymmetric tensor T = T

...i

⊗···⊗e

∈

(V ), then the action of σ ∈S

on it is given by

σ(T)=T

...i

σ(i

)

⊗···⊗e

σ(i

)

−1

)...σ

−1

)

⊗···⊗e

=sgn(σ )T

...j

⊗···⊗e

by antisymmetry of T

...j

=sgn(σ )T

so if σ is odd then T changes sign under it, and if σ is even then T is invariant.

Thus, we can restate the symmetrization postulate as follows: any state of an n-

particle system is either invariant under a permutation of the particles (in which

case the particles are known as bosons), or changes sign depending on whether the

permutation is even or odd (in which case the particles are known as fermions).

4.4 From Lie Groups to Lie Algebras

You may have noticed that the examples of groups we met in the last two sec-

tions had a couple of different ﬂavors: there were the matrix groups like SU(2) and

SO(3) which were parametrizable by a certain number of real parameters, and then

there were the ‘discrete’ groups like Z

and the symmetric groups S

that had a

ﬁnite number of elements and were described by discrete labels rather than contin-

uous parameters. The ﬁrst type of group forms an extremely important subclass of

groups known as Lie Groups, named after the Norwegian mathematician Sophus

Lie who was among the ﬁrst to study them systematically in the late 1800s. Besides

their ubiquity in math and physics, Lie groups are important because their contin-

uous nature means that we can study group elements that are ‘inﬁnitely close’ to

the identity; these are known to physicists as the ‘inﬁnitesimal transformations’ or

‘generators’ of the group, and to mathematicians as the Lie algebra of the group.

As we make this notion precise, we will see that Lie algebras are vector spaces and

as such are sometimes simpler to understand than the ‘ﬁnite’ group elements. Also,

the ‘generators’ in some Lie algebras are taken in quantum mechanics to represent

112 4 Groups, Lie Groups, and Lie Algebras

certain physical observables, and in fact almost all observables can be built out of el-

ements of certain Lie algebras. We will see that many familiar objects and structures

in physics can be understood in terms of Lie algebras.

Before we can study Lie algebras, however, we should make precise what we

mean by a Lie group. Here we run into a snag, because the proper and most general

deﬁnition requires machinery well outside the scope of this text.

We do wish to be

precise, though, so we follow Hall [8] and use a restricted deﬁnition. This deﬁnition

does not really capture the essence of what a Lie Group is, but will get the job done

and allow us to discuss Lie algebras without having to wave our hands.

That said, we deﬁne a matrix Lie group to be a subgroup G ⊂ GL(n, C) which

is closed, in the following sense: for any sequence of matrices A

∈G which con-

verges to a limit matrix A, either A ∈ G or A/∈GL(n, C). This says that a limit of

matrices in G must either itself be in G, or otherwise be noninvertible. As remarked

above, this deﬁnition is technical and does not provide much insight into what a Lie

group really is, but it will provide the necessary hypotheses in proving the essential

properties of Lie algebras.

Let us now prove that some of the groups we have encountered above are indeed

matrix Lie groups. We will verify this explicitly for one class of groups, the orthog-

onal groups, and leave the rest as problems for you. The orthogonal group O(n) is

deﬁned by the equation R

−1

,orR

R =I . Let us consider the function from

GL(n, R) to itself deﬁned by f(A)= A

A. Each entry of the matrix f(A)is easily

seen to be a continuous function of the entries of A,sof is continuous. Consider

now a sequence R

in O(n) that converges to some limit matrix R. We then have

f(R)=f



lim

i→∞



= lim

i→∞

f(R

) since f is continuous

= lim

i→∞

so R ∈ O(n). Thus O(n) is a matrix Lie group. The unitary and Lorentz groups,

as well as their cousins with unit determinant, are similarly deﬁned by continuous

functions, and can analogously be shown to be matrix Lie groups. For an example

of a subgroup of GL(n, C) which is not closed, hence not a matrix Lie group, see

Problem 4.10.

We remarked earlier, though, that the above deﬁnition does not really capture

the essence of what a Lie group is. What is that essence? As mentioned before, one

should think of Lie groups as groups which can be parametrized in terms of a certain

number of real variables. This number is known as the dimension of the Lie group,

and we will see that this number is also the usual (vector space) dimension of its

corresponding Lie algebra. Since a Lie group is parametrizable, we can think of it as

The necessary machinery being the theory of differentiable manifolds; in this context, a Lie

group is essentially a group that is also a differentiable manifold. See Schutz [15]orFrankel[4]

for very readable introductions for physicists, and Warner [18] for a systematic but terse account.