Иванищева О.И., Иванищев П.И. Стохастические модели микронеоднородных материалов
Подождите немного. Документ загружается.


21
где –
ϕ
произвольная функция. Поэтому , чтобы получить одноточечное
приближение, достаточно принять , что двухточечный момент
(
)
)2(c)2(n)1(
ελλλ ⋅−⋅
⋅
является функцией только
)2()1(
xx − . Эта
гипотеза принята в виде понятия «сильной изотропии».
К тем же результатам можно прийти , пренебрегая в двухточечном
моменте
(
)
)2(c)2(n)1(
ελλλ ⋅−⋅
⋅
составляющими , зависящими от
направления вектора
)2()1(
x
x
−
.
Таким образом, для изотропного в микро- и макрообъемах материала
погрешность одноточечного приближения определяется зависимостью
двухточечного момента , содержащего тензор деформаций от направления
вектора
)2()1(
x
x
−
. Сравнение результатов одноточечного приближения для
материалов зернистой и однонаправленной волокнистой структуры с
экспериментальными данными и другими расчетами показывает, что эта
зависимость несущественна .
Однако существуют такие виды структур, специфику свойств которых
одноточечное приближение не учитывает . Например, в рамках этого
приближения, свойства материала, армированного хаотически направленными
непрерывными волокнами , не отличаются от свойств материала,
армированного сферическими включениями . Однако исходя из опыта , следует,
что они различны , особенно, в случае высокомодульных наполнителей .
Одноточечное приближение не позволяет описать анизотропию свойств
композиционных материалов , связанную с ориентацией структурных
элементов , например, матрицы с ориентированными эллипсоидальными
включениями . В то же время, корреляционное приближение улавливает этот
эффект, поскольку формула (2.3.3) содержит двухточечный момент упругих
характеристик композиционного материала.
2.5 Теория условных моментных функций
Уточнение одноточечного приближения путем учета двухточечных
моментов приводит к существенному усложнению уравнений. Задачу можно
существенно упростить , если вместо метода моментов воспользоваться
методом условных моментов . Сущность его состоит в следующем .
Пусть композиционный материал состоит из
n
компонентов с
объемными концентрациями и тензорами модулей упругости соответственно
kk
,c
λ
,
n
,...
2
,
1
k
=
. Тогда, пользуясь представлением (2.4.4), где плотность
распределения модулей упругости
(
)
λ
1
f для
n
-компонентного материала
имеет вид
()
∑
=
−=
n
1
k
kk1
c)(f λλδλ
, (2.5.1)
получим на основе (2.2.18) выражение для тензора средних напряжений
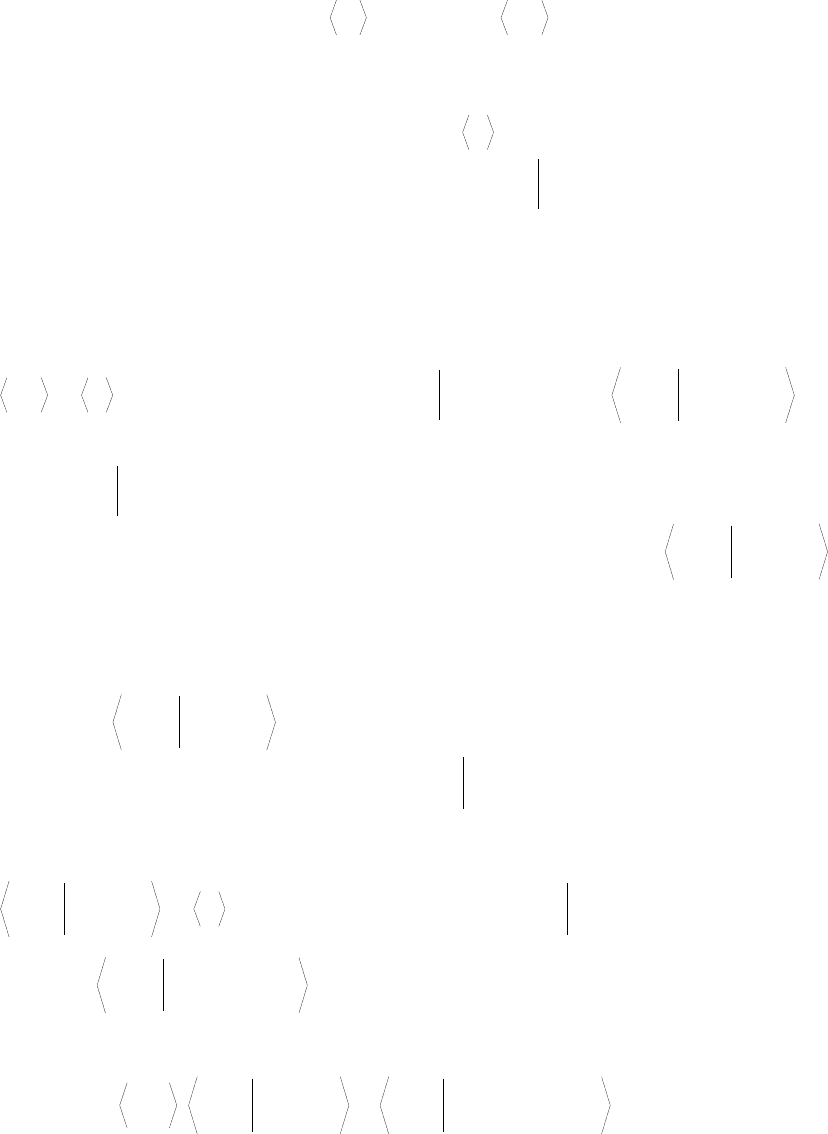
22
∑
=
=
n
1
k
kkk
c ελσ . (2.5.2)
Отсюда следует, что для определения макроскопических упругих
постоянных необходимо найти средние деформации компонентов как функции
средних средних деформаций всего тела
ε
.
Умножим (2.2.20) на
(
)
)1()2()2()1(
,,f νλεε -условную плотность
распределения деформаций в точках
)2()1(
x,x и модулей упругости в точке
)2(
x
при условии , что в точке
)1(
x
находится компонент
ν
,
и проведем
осреднение. В результате получим систему
уравнений
(
)
(
)
(
)
)1(
)2(
k
)2(c
k
n
1
k
)1(
)2(
k
)2()1(
,fxxG νελλεε
νν
⋅−⋅−+=
∑
=
, (2.5.3)
n
,...
2
,
1
=
ν
,
где
(
)
)1(
)2(
k
f
ν
- вероятность нахождения в точке
)2(
x
компонента
k
при
условии, что в точке
)1(
x
находится компонент
ν
;
)1(
)2(
k
)2(
,
ν
ε⋅
-
математическое ожидание тензора деформаций в точке
)2(
x
при условии, что в
ней находится компонент
k
, а в точке
)1(
x
находится компонент
ν
.
В уравнения (2.5.3) вошли неизвестные условные двухточечные
моменты
)1(
)2(
k
)2(
,
ν
ε⋅
. Для их определения умножим уравнение (2.2.20) на
условную плотность ),,,(f
3
)1(
k
)2()2()1(
ν
λεε и проведем осреднение. Тогда
получим
.n...2,1,k,,,)
(),(f)xx(G,
)3(
)1(
k
)2(
r
)2(
c
n
1r
r
)3(
)1(
k
)2(
r
)2()1()3(
)1(
k
)1(
=⋅−
−⋅⋅−+=
∑
=
νελ
λεε
ν
νν
(2.5.4)
Продолжая этот процесс, получим бесконечную систему уравнений
относительно неизвестных условных моментов
,...,...,,,...,,
)i()2()1(
)1(
)2()1(
)1(
i2121
1
ννννν
ν
εεε (2.5.5)
n,...,2,1,
,...21
=
ν
ν
Замыкание полученной системы может быть осуществлено путем обрыва
процесса на некотором шаге. Здесь , в частности , возможны варианты

23
0,...,,
)i()2()1(
)1(
i21
=
ννν
ε
εε
ννν
=
)i()2()1(
)1(
i21
,...,, (2.5.6)
1
i21
)i()2()1(
)1(
,...,,
ν
ννν
εε =
.
Для решения полученных уравнений необходимо задать условные
плотности распределения компонентов
),...,...,(f),...,,(f),,(f
)i()3(
)2(
)1()3(
)2(
)1()2()1(
i3
2
13
2
121
νν
ν
νν
ν
ννν
При этом «компонент» можно трактовать не только как структурный
элемент с определенными физическими свойствами , но включать сюда также
его ориентацию , форму , размеры и другие геометрические параметры .
Если ограничиться двухточечными условными плотностями
распределения компонентов , то достаточно рассмотреть уравнение (2.5.3). Для
его замыкания целесообразно принять третье условие (2.5.6) т.е.
k
)1(
)2(
k
)2(
, εε
ν
=
(2.5.7)
Это соответсвует пренебрежению флуктуациями деформаций в пределах
каждого компонета .
В результате получим систему алгебраических уравнений относительно
средних по компонентам деформаций
(
)
∑
=
−⋅⋅+=
n
1
k
k
c
kk
)x(p)x(G ελλεε
νν
(2.5.8)
n
,...
2
,
1
=
ν
,
где принято обозначение
)(f)xx(p
)1(
)2(
k
)2()1(
k νν
=− . (2.5.9)
Если принять
0)x(p)x(G
k
=
ν
, где
)x(G
определено соотношениями
(2.4.2), то уравнения (2.5.8) будут равносильны уравнениям одноточечного
приближения (2.4.3). В самом деле, в этом случае уравнения (2.5.8) примут вид
(
)
∑
=
−∞+⋅+=
n
1
k
k
c
kkk
)c)(G)x()0(G( ελλδεε
νν
(2.5.10)
n
,...
2
,
1
=
ν
.
Умножая (2.5.10) на
m
c
νν
λ
и проводя суммирование, получаем
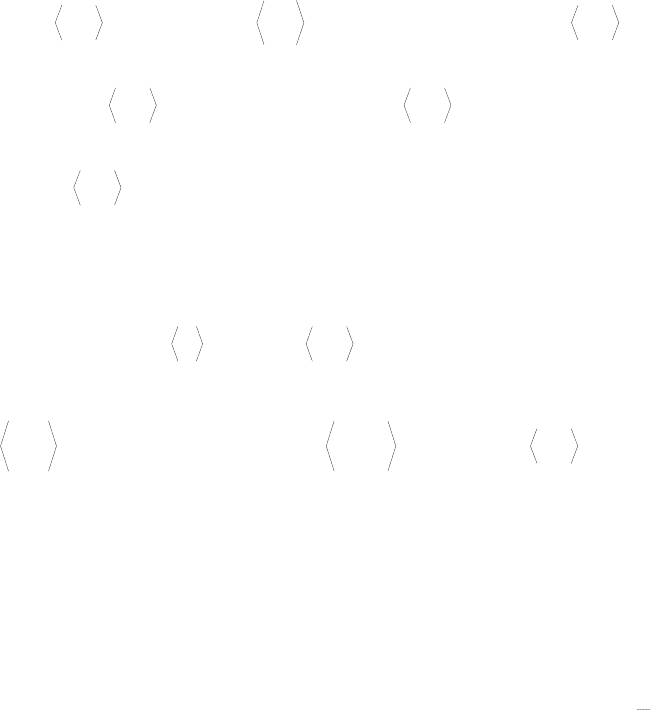
24
)c)c
cc)((G)c
c()0(Gcc
n
1
m
n
1
k
k
k
c
n
1
m
n
1k
k
k
k
n
1k
k
m
k
k
c
n
1k
k
1m
k
k
n
1
m
n
1
m
∑∑
∑∑∑
∑∑∑
=
=
===
=
+
==
⋅−
−⋅∞+−
−⋅+=
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
νν
ν
λελ
λελελλ
ελελελ
(2.5.11)
Учитывая соотношения
∑
=
=
n
1
k
k
k
c εε ;
∑
=
=
n
1
k
m
kk
m
c λλ ;
∑
=
=
n
1
k
kkk
m
c ελελ , (2.5.12)
приходим к выводу, что уравнения (2.4.2) и (2.5.11) равносильны .
Таким образом, уравнения (2.5.8) более точно описывают
композиционный материал по сравнению с одноточечным приближением и
дают возможность учитывать более сложные структуры . Наличие
двухточечной условной плотности
()
k
px
ν
позволяет описать анизотропию
свойств композиционного материала, связанную с геометрией структуры , что
проявляется в зависимости
)x(p
k ν
от направления радиуса - вектора
x
.
3.Прогнозирование макроскопических коэффициентов
теплопроводности, стохастически неоднородных материалов.
3.1. Основные уравнения. Решения для слоистых, зернистых и
волокнистых материалов.
Рассмотрим неограниченное твердое тело , тензор теплопроводности
которого
ij
a образует статистически однородное случайное поле. Масштабы
корреляции функции
a
будем считать конечными , тем самым предполагая
выполнение условий эргодичности случайных полей . Таким условиям обычно
удовлетворяют реальные композиционные материалы , структура которых
имеет случайный характер, а средние размеры компонентов пренебрежимо
малы по сравнению с размерами тела.
Вследствие случайного характера свойств материала при неравномерном
нагреве температура
Θ
и тепловые потоки
j
q также будут случайными
функциями координат. При этом зависимости между тепловыми потоками и
градиентами температуры выражаются законом Фурье

25
k,jkj
aq
Θ
−
=
3
,
2
,
1
k
,
j
=
(3.1.1)
Уравнение баланса тепла в условиях стационарной теплопроводности и
отсутствия внутренних источников тепла имеет вид
0q
j,j
=
. (3.1.2)
Задача состоит в том, чтобы при известных статистических
характеристиках случайного поля тензора теплопроводности
ij
a
определить
макроскопический тензор теплопроводности
∗
ij
a .
Предположим, что композиционный материал находится в таких условиях
неравномерного стационарного нагрева, при которых случайные поля тепловых
потоков
j
q и градиентов температуры
j,
Θ
являются статистически
однородными . В этом случае их можно считать эргодическими , т.е. средние по
статистическому ансамблю тепловые потоки
j
q и градиенты температуры
j,
Θ
равны соответствующим средним по объему :
∫
∞→
= dvq
v
1
limq
j
v
j
;
∫
∞→
= dv,
v
1
lim,
j
v
j
ΘΘ
. (3.1.3)
Зависимости между средними тепловыми потоками и градиентами
температуры выражаются законом Фурье
k,
jk
j
aq Θ
∗
−=
3
,
2
,
1
k
,
j
=
, (3.1.4)
где
∗
ij
a - макроскопический тензор теплопроводности .
Представим случайные функции
ij
a ,
j
q ,
Θ
в виде суммы математических
ожиданий и флуктуаций
0
ijijij
aaa +=
0
jjj
qqq +=
0
ΘΘΘ += . (3.1.5)
Тогда из (3.1.1) получаем выражение среднего теплового потока в виде
0
k,
0
jkk,jkj
aaq ΘΘ ⋅−−= (3.1.6)
Подставляя (3.1.1), (3.1.5) в уравнение баланса тепла (3.1.2), получаем
уравнение теплопроводности относительно флуктуаций температуры
j
,
0
k,k
0
jk
0
jkjk
)),(a(,a ΘΘΘ +−= .
(3.1.7)
При этом средняя температура определяется формулой
jj,
x⋅= ΘΘ . (3.1.8)
т.е. не ограничена на бесконечности , поэтому флуктуации температуры
0
Θ
можно считать пренебрежимо малыми при
∞
→
x
и дополнить уравнение
(3.1.7) условием на бесконечности
(
)
.0x
x
0
→
∞→
Θ (3.1.9)

26
Таким образом, для определения макроскопического тензора
теплопроводности
∗
ij
a необходимо найти решение уравнения (3.1.7).
Подставляя затем градиенты
0
j,
Θ
в выражение (3.1.6), найдем зависимости
между средним тепловым потоком и средними градиентами температуры
(3.1.4).
Уравнение (3.1.7) является статистически нелинейным. Оно приводится к
бесконечной последовательности связанных уравнений относительно моментов
различных порядков и типов , решить которую в общем случае не
представляется возможным. Исключение представляет случай слоистой
структуры среды, когда тензор теплопроводности
ij
a является функцией одной
координаты .
Пусть , например, тензор
ij
a
зависит только от координаты
3
x . Вследствие
однородности макроскопических тепловых потоков и градиентов температуры
случайные функции
Θ
,q
j
также будут зависеть только от координаты
3
x . В
этом случае уравнение (3.1.7) легко интегрируется , в результате чего имеем
3k
3,
1
3333
0
k,
1
a
1
a
1
δΘΘ ⋅⋅
−=
−
. (3.1.10)
Подставляя (3.1.10) в (3.1.6), получим зависимости между средними
тепловыми потоками и градиентами температуры
k,3k3j
1
3333
3j
jkj
a
a
1
a
a
aq Θδ ⋅
⋅
−⋅+−=
−
. (3.1.11)
Отсюда следует , что макроскопический тензор теплопроводности
определяется выражением
3k3j
1
3333
3j
jk
jk
a
a
1
a
a
aa δ ⋅
−⋅+=
−
∗
(3.1.12)
Если слоистый материал составлен из изотропных слоев , т.е. в каждой его
точке тензор
ij
a имеет вид
ijij
aa
δ
⋅
=
, (3.1.13)
то макроскопические коэффициенты теплопроводности вдоль слоев и в
поперечном направлении будут, соответственно ,
aa
1
=
∗
1
3
a
1
a
−
∗
= . (3.1.14)
Для материалов , имеющих объемные концентрации и коэффициенты
теплопроводности слоев
)i(
i
a,c , одноточечная плотность распределения
коэффициентов теплопроводности определяется формулой

27
)aa(c)a(f
)i(
i
n
1
i
1
−=
∑
=
δ , (3.1.15)
где
n
– число слоев с различными свойствами .
При этом статистические средние (3.1.14) будут иметь вид
∑
∫
=
⋅=⇒⋅⋅=
n
1
i
)i(
i1
acada)a(faa , (3.1.16)
)
a
c
(
a
1
da)a(f
a
1
a
1
n
1i
)i(
i
1
∑
∫
=
=⇒⋅⋅=
.
Таким образом, соотношения (3.1.14), (3.1.16) представляют точное
решение задачи о нахождении макроскопических постоянных
теплопроводности многокомпонентного слоистого материала с изотропными
слоями. В случае двухкомпонетного материала из (3.1.14), (3.1.16) следует
aa
1
=
∗
;
()
)3(
12
2)3(
21
j
acca
)a(cc
aa
⋅−+
⋅⋅
−=
∗
(3.1.17)
)2()1()3(
a
a
a
−
=
.
Для материалов зернистой, волокнистой структуры , а также для
материалов пространственного армирования построение точного решения из-
за значительных математических трудностей не представляется возможным.
Поэтому далее рассмотрим приближенные методы решения указанного типа
задач.
Для композиционных материалов , состоящих из изотропных
компонентов , соотношения (3.1.6), (3.1.7) примут вид
j,
0
j,j
aaq ΘΘ ⋅−⋅−=
.))(a(a
k,
0
k,k,
00
kk,
ΘΘΘ +−=⋅ (3.1.18)
Введем корреляционные функции
)y(S)x(a)yx(
00
=⋅+Θ
)y(K)x(a)yx(a
00
=⋅+ , (3.1.19)
которые в силу однородности рассматриваемых случайных полей зависят
только от разности координат двух точек
y
. Первое из уравнений (3.1.18) при
этом можно записать в виде
).0(Saq
ijj,j
−⋅−= Θ (3.1.20)

28
Умножим второе из уравнений (3.1.2), взятое в точке
x
на
)yx(x
0
+
и
проведем статистическое осреднение. Пренебрегая моментами третьего
порядка , т.е. ограничиваясь корреляционным приближением , получаем
дифференциальное уравнение относительно функции
(
)
yS
k,kk,kk,
KSa Θ ⋅−=⋅
(3.1.21)
Поскольку корреляционные связи между рассматриваемыми случайными
функциями , взятыми в различных точках, убывают с увеличением расстояния
между ними , то функции
0
)
x
(
K
),
x
(
S
→
при
∞
→
x
.
Таким образом, для определения макроскопических коэффициентов
теплопроводности необходимо найти решение уравнения (3.1.21) при нулевых
условиях на бесконечности и подставить его в (3.1.20).
В случае слоистой структуры материала, когда коэффициент
теплопроводности является случайной функцией одной переменной ,
корреляционные функции
)
x
(
K
),
x
(
S
будут зависеть только от
координаты
3
y . Выражение (3.1.20) примет вид
3j3,
j,
j
)0(Saq δΘ ⋅−−= , (3.1.22)
а дифференциальное уравнение (3.1.21) становится обыкновенным
3,3,33,
KSa Θ−= . (3.1.23)
Интегрируя его, находим
3,3,
a
)0(K
)0(S Θ⋅−= . (3.1.24)
Теперь из (3.1.22), (3.1.24) получаются зависимости между средними
тепловыми потоками и градиентами температуры
j,1j
aq Θ ⋅−=
∗
;
3,13
aq Θ ⋅−=
∗
(
2
,
1
j
=
) , (3.1.25)
где макроскопические коэффициенты теплопроводности имеют вид
aa
1
=
∗
,
a
)0(K
aa
3
−=
∗
. (3.1.26)
Если материал составлен из двух компонентов с объемными
концентрациями и коэффициентами теплопроводности
)2(
2
)1(
1
a,c,a,c
соответственно, то , пользуясь плотностью распределения (3.1.15) и
соотношениями (3.1.26), получаем
)2(
2
)1(
1
1
acaca +=
∗
;
=
)
0
(
K
2)2()1(
2
1
)aa(cc −
. (3.1.27)
Точные решения (3.1.17) для двухкомпонентной слоистой среды можно
представить следующим образом:
aa
1
=
∗
,
)3(
12
3
a)cc(a
)0(K
aa
⋅−−
−=
∗
. (3.1.28)

29
Как видим, коэффициент
∗
3
a из (3.1.26), полученный на основе
корреляционного приближения теории случайных функций, представляет
собой первый член разложения точного решения для
∗
3
a в ряд по
степеням
)3(
1
2
a)cc( ⋅− . При равных концентрациях компонентов
2
1
cc
=
решения (3.1.26 ) совпадают с точными .
Рассмотрим общий случай пространственной неоднородности
коэффициента теплопроводности , что соответствует материалам зернистой
структуры , а также композиционным материалам, армированным
искривленными или разнонаправленными волокнами. Решение уравнения
(3.1.18) в этом случае можно представить следующим образом:
(
)
(
)
(
)
∫
⋅⋅−⋅= xdx,KxyGyS
kk,
Θ . (3.1.29)
Здесь функция Грина имеет вид
(
)
x
1
a4
1
xG ⋅
⋅⋅
=
π
(3.1.30)
Если ориентация зерен или волокон имеет хаотический характер, т.е.
равновероятна во всех направлениях, то случайное поле коэффициента
теплопроводности
a
будет статистически изотропным то корреляционная
функция
(
)
yK будет зависеть только от длины пространственного вектора
y . Тогда из выражения (3.1.29) находим
()
∫∫
⋅⋅
⋅
⋅⋅=
∞
Ω
Ω
π
Θ
ddp
p
yy
dp
dK
a4
,
0S
2
kj
0
k
j,
, (3.1.31)
где
Ω
- телесный угол.
Пользуясь соотношением
jk
2
kj
a
3
4
d
p
yy
δΩ
Ω
⋅=⋅
∫
, (3.1.32)
получаем окончательно
j,j,
a3
)0(K
)0(S Θ⋅
⋅
−= . (3.1.33)
Из (3.1.20) и (3.1.33) следует зависимость между средними тепловыми
потоками и градиентами температуры
jj,
,aq Θ ⋅−=
∗
, (3.1.34)
где макроскопический коэффициент теплопроводности
∗
a
определятся
соотношением

30
a3
)0(K
aa
⋅
−=
∗
. (3.1.35)
Рассмотрим однонаправленный волокнистый материал, волокна
которого ориентированы вдоль оси
3
x
. В этом случае коэффициент
теплопроводности будет случайной функцией координат
2
1
x,x , а второе из
уравнений будет двумерным. Представим его решение в интегральной форме
(
)
(
)
(
)
∫
⋅⋅−⋅= xdx,KxyGyS
kk,
Θ
,
2
,
1
k
=
(3.1.36)
где функция Грина
(
)
xG имеет вид
()
()
2
1
jj
xxln
a4
1
xG
−
⋅=
π
,
2
,
1
j
=
(3.1.37)
Для реальных однонаправленных волокнистых материалов характерно
хаотическое расположение волокон, поэтому случайное поле
a
будут
статистически изотропным в плоскости
2
1
x,x , а его корреляционная функция
зависит только от длины
ρ
вектора y в плоскости
2
1
x,x . Тогда из выражений
(3.1.36), (3.1.37) , находим
()
∫∫
⋅⋅⋅
⋅
=
∞ π
ϕρ
ρ
ρπ
Θ
2
0
2
kj
0
k,
j,
dd
yy
d
dK
a2
0S , (3.1.38)
где
ϕ
– угол в полярной системе координат.
Пользуясь соотношением
jk
2
0
2
kj
ad
yy
δϕ
ρ
π
⋅=⋅
⋅
∫
(3.1.39)
, получим
jj,
,
a2
)0(K
)0(S Θ⋅−=
. (3.1.40)
Подставляя (3.1.40) в уравнение (3.1.20), найдем соотношения между
средними тепловыми потоками и градиентами температуры
j1j
,aq Θ ⋅−=
∗
,
333
,aq Θ ⋅−=
∗
,
2
,
1
j
=
, (3.1.41)
где макроскопические коэффициенты теплопроводности в поперечном и
продольном направлениях относительно волокон имеют вид
a2
)0(K
aa
⋅
−=
∗
, aa
3
=
∗
. (3.1.42)
Результаты , полученные на основе корреляционной теории, применимы
только для расчета свойств материалов с малыми флуктуациями коэффициента
теплопроводности . Более точные решения, справедливые при больших
