Ismail M., Koelink E. (editors) Theory and Applications of Special Functions
Подождите немного. Документ загружается.


48
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Proof.
If N
=
0, the sum on the right is
-
-
a' (q/a; q)j
(q-
j
;
q)
(by (Andrews, 1976, p. 35, eq. (3.3.6))
(4; 4)j
for all
j
>=
0.
.
-
If, on the other hand,
j
=
0,
the sum on the right is equal to
1
which
L
We can conclude the proof of the proposition by showing that the
right-hand side of the asserted identity satisfies the recurrence given
in Proposition
2.4
thus permitting a double induction on N and
j
to
conclude matters.
We denote by R(N,
j)
the right-hand side of the equation asserted in
the proposition.

a-Gaussian Polynomials 49
and Proposition 2.8 is proved.
0
Proposition
2.9.
For
N
and
j
nonnegative integers
Proof.
(by (Andrews, 1976, p. 36, eq. (3.3.6)))
by the finite geometric series summation.
0
3.
Limiting Cases and Identities
The previous section described fundamental formulas and recurrences
for the a-Gaussian polynomials. In this section, we examine the limiting
values of these polynomials (Propositions 3.1 and 3.2), and we show how
they
fit
into a generalized Chu-Vandermonde summation (Proposition
3.3). Proposition 3.4 provides a useful reduction formula.
Proposition
3.1.
For la1
<
1,
141
<
1,
Proof.
-
1
--
(by (Andrew~, 1976, p. 36, eq. (3.3.7))).
(a; q)
M

50
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Proposition
3.2.
If la1
<
1,
141
<
1,
and
A,
B,
C
and
D
are integers
with
A
>
C
>
0,
then
Proof.
CN+D
~im
[AN+B
;
q,
a
=
lim
~+m
CN+D
]
N-m
C
h=O
by (Andrews, 1976, p. 19, eq. (2.2.5)).
Proposition
3.3.
If
R, N,
and
j
are non-negative integers then
Proof.
We shall prove this result by showing that the right-hand side
does not depend on
R
and is equal to the left-hand side when
R
=
0
(the latter is immediately obvious).

a- Gaussian Polynomials
51
R+
1
i
(i-l)(n+i-1-j-R-1)
+Can
R
j-i
;
4, a
i=o
I
Thus the sum on the right-hand side of the asserted identity is unaltered
when
R
is replaced by
R
+
1.
Consequently it is equal to its value at
.-
-
R
=
0
which is
0
Proposition
3.4.
For nonnegative integers r,
n,
m,
Proof.
We proceed by induction on
r.
When
r
=
0,
the assertion is a
tautology.
At
r
+
1,
n+m
=
2
aj(-l)jq~) (qrn; qlj
[
;
q]
[
n-j
;
q, a]
j=O

52
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
r+l
n+m
~~3(-l)j~(j;')+~
(qm;q)j
[
j-1
;q]
[
n-j ;q,a
j=O
r+l
n+m
=
c
aj(-l)jq(:)
(qm; q)j
[
n-j
;
q7 a]
([
s
;
q]
+
qr-j+'
[
;
q])
j=O
~+l
n+m
=
c
aj(-l)jq(:) (qm; qlj
[
+
l
;
q]
[
;
q, a]
3
n-j
j=O
(by (Andrews,
1976,
p.
35,
eq.
(3.3.3))).
Hence Proposition
3.4
follows by induction on
r.
0
4.
a-Generalizations of Finite
Rogers-Ramanujan Type Identities
In Section
1,
equation
(1.11)
is the special case
k
=
2,
m
=
N
of the
following result:
Theorem
4.1.
For
m,
N, k nonnegative integers with k
>
0
C(
1)s
ks
s((2k+l)s-1112 N+m+l-ks
-
aq
[:
;4]
[
m-ks
szo
Remark
4.2.
If
we let
m,
N
-+
oo
take k
=
1 and invoke Propositions
3.1
and
3.2,
we retrieve (1.5) term
by
term.
Proof.
Call the left side of this identity
L(m)
and the right side
R(m).
We proceed by induction on
m.
Clearly
L(0)
=
R(0)
=
1.

a-Gaussian Polynomials
Furthermore, it is immediate that
00
where
[am] zqai
=
Cm.
j=O
On the other hand,
N+m+l-ks
N+m-ks
x([
m-ks
m-ks-1
1)s
ks
s((2k+l)s-1)/2
=C(-
a
9
m-lcs-1
N
+
m
-
ks
[
m-ks
szo
(by
Proposition
2.6)
C(-l)sq(;)+ms
N+m-ks
[r
''1
[
m-ks
szo
Hence the object of proving
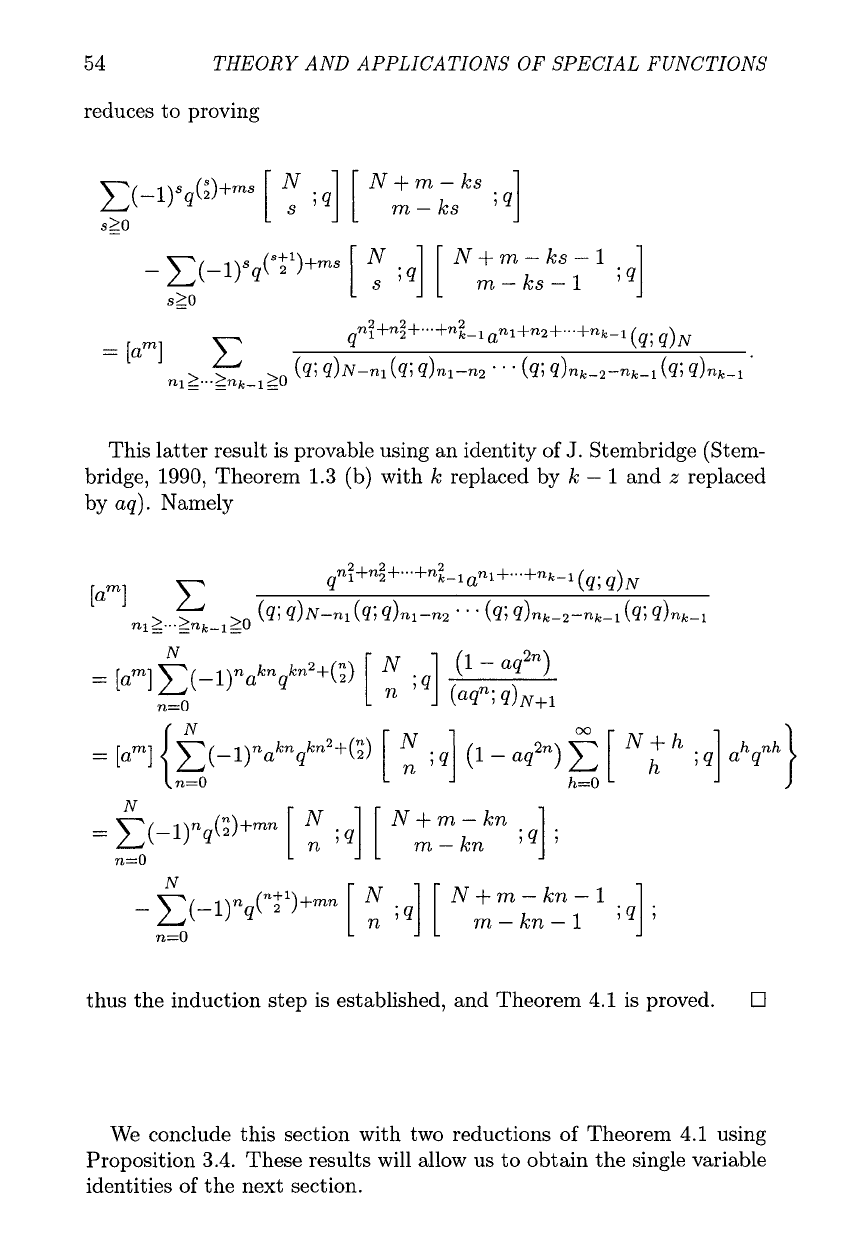
54
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
reduces to proving
x(-l)sq(;)+ms
N+m-ks
[
y
;q]
[
m-ks
320
This latter result is provable using an identity of
J.
Stembridge (Stem-
bridge, 1990, Theorem 1.3 (b) with
k
replaced by
k
-
1
and
z
replaced
by
aq).
Namely
thus the induction step is established, and Theorem 4.1 is proved.
We conclude this section with two reductions of Theorem 4.1 using
Proposition
3.4.
These results will allow us to obtain the single variable
identities of the next section.

a-
Gaussian Polynomials
Corollary
4.3.
For
m,
N, k
nonnegative integers with
k
>
0
N+m+l-ks N+m-ks
([
m-ks-j
m-ks-j-1
;
9, aq])
Proof.
Apply Proposition
3.4
(with
r
=
s
-
1
and a replaced aq) to each
of the a-Gaussian polynomials in Theorem
4.1.
The terms with
s
=
0
are instead combined using Proposition
2.5.
0
Corollary
4.4.
For
m,
N, k
non-negative with
k
>
0
N+m+l-ks N+m-ks
([
m-ks-j m-ks-j-1
;
9, a])
.
Proof.
Apply Proposition
3.4
(with
r
=
s)
to each of the a-Gaussian
polynomials in Theorem
4.1.
0
5.
Single Variable Polynomial
Rogers-Ramanujan Generalizations
Schur (Schmiidgen,
1990)
was the first to prove the Rogers-Ramanujan
identities as a limiting case of polynomial identities. Namely, he proved

THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
56
and
The relationship of (5.1) and (5.2) to more general results is discussed
extensively in (Andrews, 1989, esp. 59).
To everyone's surprise, David Bressoud (Bressoud, 1981b) found a
completely different polynomial refinement:
and
n
j=O
OC)
(5.4)
Identities
(5.3)
and (5.4) have been placed in the context of more general
q-hypergeometric identities (Andrews and Berkovich, 2002).
The list does not stop here. At least two further polynomial refine-
ments of the Rogers-Ramanujan identities have been found (Andrews,
1974), (Andrews, 1990, p.
3,
eqs. (1.11) and (1.12)). Most recently,
S.
0.
Warnaar (Warnaar, 2002) has found extensive partial sum Rogers-
Ramanujan identities.
It should be noted that in each of the examples given above (and in
those alluded to in (Andrews, 1974) and (Andrews, 1989)) all the sums
terminate naturally. In other words, the index of summation is extended
over all values that produce non-zero summands.
As we shall see, we may set
a
=
1
in Corollary 4.3 and
a
=
q in
Corollary 4.4 in order to obtain
partial sums
of the Rogers-Ramanujan
polynomial. Our results are quite different from those of Warnaar in
(Warnaar, 2002).
To this end we require a definition and a lemma.
n
Definition
5.1.
En(x, q)
=
lim
N+m
We remark in passing that Euler proved (~ndrews, 1976, p. 19,
eq.
1
1
(2.2.5))
Em
(x, q)
=
-
.
(x;
dOC)
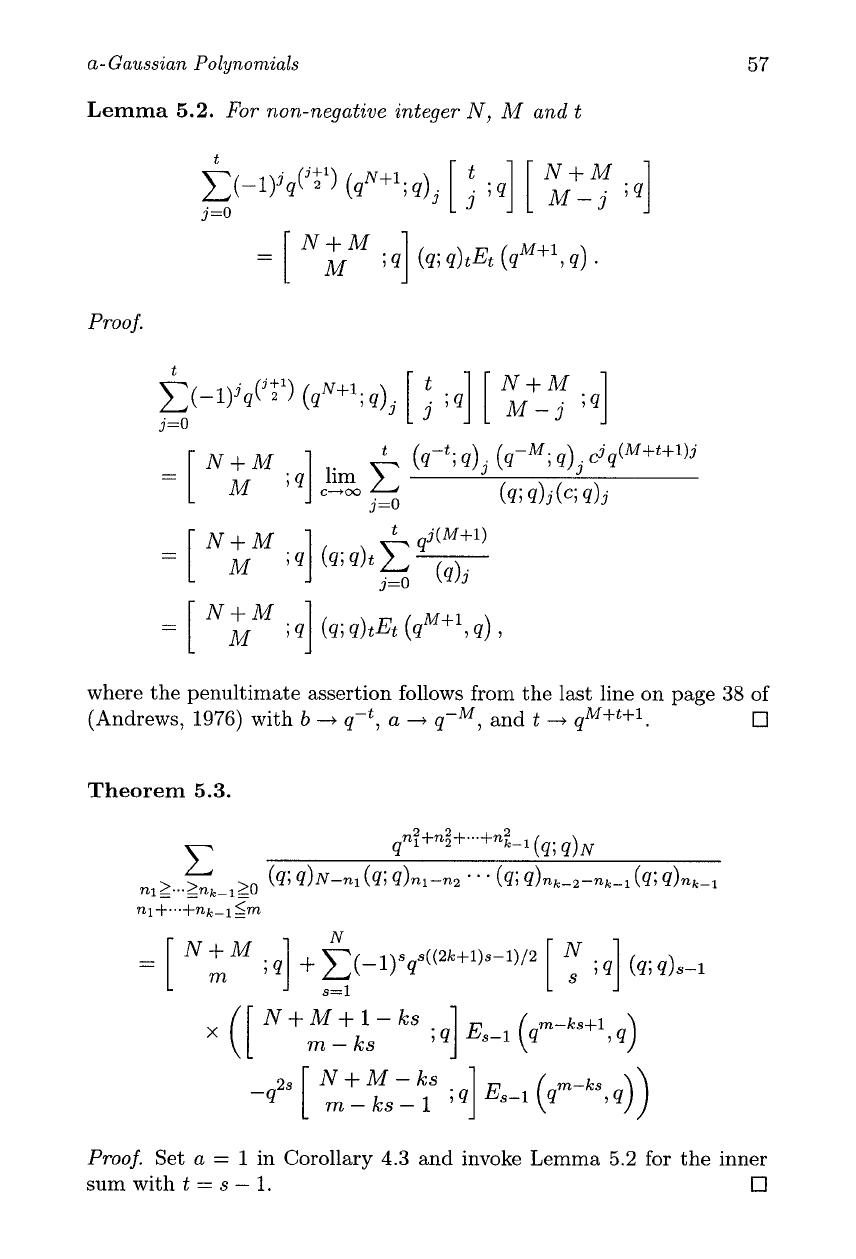
a-Gaussian Polynomials
Lemma
5.2.
For non-negative integer
N, M
and
t
Proof.
where the penultimate assertion follows from the last line on page
38
of
(Andrews, 1976) with
b
--t
qdt,
a
--t
q-",
and
t
-t
q"+t+l.
0
Theorem
5.3.
N+M+l-ks
x([
m-ks
Proof.
Set
a
=
1
in Corollary
4.3
and invoke Lemma
5.2
for the inner
sum with
t
=
s
-
1.
0
