Hull J.C. Risk management and Financial institutions

Подождите немного. Документ загружается.

Model Risk and

Liquidity Risk

In this chapter we discuss two additional types of risk faced by financial

institutions: model risk and liquidity risk. Model risk is the risk related to

the models a financial institution uses to value derivatives. Liquidity risk

is the risk that there may not be enough buyers (or sellers) in the market

for a financial institution to execute the trades it desires. The two risks are

related. Sophisticated models are only necessary to price products that are

relatively illiquid. When there is an active market for a product, prices can

be observed in the market and models play a less important role.

There are two main types of model risk. One is the risk that the model

will give the wrong price at the time a product is bought or sold. This can

result in a company buying a product for a price that is too high or selling

it for a price that is too low. The other risk concerns hedging. If a

company uses the wrong model, the Greek letters it calculates—and the

hedges it sets up based on those Greek letters—are liable to be wrong.

Liquidity risk is the risk that, even if a financial institution's theoretical

Price is in line with the market price and the price of its competitors, it

cannot trade in the volume required at the price. Suppose that the offer

Price for a particular option is $40. The financial institution could

Probably buy 10,000 options at this price. But it is likely to be quite

difficult to buy 10 million options at or close to the price. If the financial

institution went into the market and started buying large numbers of

options from different market makers, then the price of the option would

Probably go up, making the rest of its trades more expensive.

344 Chapter 15

15.1 THE NATURE OF MODELS IN FINANCE

Many physicists work in the front and middle office of banks and many of

the models they use are similar to those encountered in physics. For

example, the differential equation that leads to the famous Black-Scholes

model is the heat-exchange equation that has been used by physicists for

many years. However, as Derman has pointed out, there is an important

difference between the models of physics and those of finance.

The models

of physics describe physical processes and are highly accurate. By contrast,

the models of finance describe the behavior of market variables. This

behavior depends on the actions of human beings. As a result the models

are at best approximate descriptions of the market variables. This is why

the use of models in finance entails what is referred to as "model risk".

One important difference between the models of physics and the

models of finance concerns model parameters. The parameters of models

in the physical sciences are usually constants that do not change. The

parameters in finance models are often assumed to be constant for the

whole life of the model when the model is used to calculate an option

price on any particular day. But the parameters are changed from day to

day so that market prices are matched. The process of choosing model

parameters is known as calibration.

An example of calibration is the choice of the volatility parameter in the

Black-Scholes model. This model assumes that volatility remains constant

for the life of the model. However, the volatility parameter that is used in

the model changes daily. For a particular option maturing in three months,

the volatility parameter might be 20% when the option is valued today,

22% when valued tomorrow, and 19% when valued on the next day. For

some models in finance, the calibration process is quite involved. For

example, calibrating an interest rate model on a particular day involves

(a) fitting the zero-coupon yield curve observed on that day and (b) fitting

the market prices of actively traded interest rate options such as caps and

swap options.

Sometimes parameters in finance models have to be calibrated to

historical data rather than to market prices. Consider a model involving

both an exchange rate and an equity index. It is likely that the correlation

between the exchange rate movements and the equity price movements

would be estimated from historical data because there are no actively

traded instruments from which the correlation can be implied.

See E. Derman, My Life as a Quant: Reflections on Physics and Finance, Wiley, 2004

Model Risk and Liquidity Risk 345

15.2 MODELS FOR LINEAR PRODUCTS

Pricing linear products such as forward contracts and swaps is straight-

forward and relies on little more than present value arithmetic. There is

usually very little disagreement in the market on the correct pricing models

for these products and very little model risk. However, this does not mean

that there is no model risk. As indicated in Business Snapshot 15.1, Kidder

Peabody's computer system did not account correctly for funding costs

when a linear product was traded. As a result the system indicated that one

of the company's traders was making a large profit when in fact he was

making a huge loss.

Another type of model risk arises when a financial institution assumes

a product is simpler than it actually is. Consider the interest rate swap

market. A plain vanilla interest rate swap such as that described in

Section 2.3 can be valued by assuming that forward interest rates will

be realized as described in Appendix B. For example, if the forward

interest rate for the period between 2 and 2.5 years is 4.3%, we value the

swap on the assumption that the floating rate that is exchanged for fixed

at the 2.5-year point is 4.3%.

Business Snapshot 15.1 Kidder Peabody's Embarrassing Mistake

Investment banks have developed a way of creating a zero-coupon bond, called

a strip, from a coupon-bearing Treasury bond by selling each of the cash flows

underlying the coupon-bearing bond as a separate security. Joseph Jett, a

trader working for Kidder Peabody, had a relatively simple trading strategy.

He would buy strips and sell them in the forward market. The forward price of

the strip was always greater than the spot price and so it appeared that he had

found a money machine! In fact the difference between the forward price and

the spot price represents nothing more than the cost of funding the purchase

of the strip. Suppose, for example, that the three-month interest rate is 4% per

annum and the spot price of a strip is $70. The three-month forward price of

the strip is 70e

0.04x3/12

= $70.70.

Kidder Peabody's computer system reported a profit on each of Jett's trades

equal to the excess of the forward price over the spot price ($0.70 in our

example). By rolling his contracts forward, Jett was able to prevent the

funding cost from accruing to him. The result was that the system reported

a profit of $100 million on Jett's trading (and Jett received a big bonus) when

in fact there was a loss in the region of $350 million. This shows that even large

financial institutions can get relatively simple things wrong!

346

Chapter 15

It is tempting to generalize from this and argue that any agreement to

exchange cash flows can be valued on the assumption that forward rates

are realized. This is not so. Consider, for example, what is known as a

LIBOR-in-arrears swap. In this instrument the floating rate that is observed

on a particular date is paid on that date (not one accrual period later as is

the case for a plain vanilla swap). A LIBOR-in-arrears swap should be

valued on the assumption that the realized interest rate equals the forward

interest rate plus a "convexity adjustment". As indicated in Business

Snapshot 15.2, financial institutions that did not understand this lost

money in the mid-1990s.

15.3 MODELS FOR ACTIVELY TRADED PRODUCTS

When a product trades actively in the market, we do not need a model to

know what its price is. The market tells us this. Suppose, for example,

that a certain option on a stock index trades actively and is quoted by

market makers as bid $30 and offer $31. Our best estimate of its current

value is the mid-market price of $30.50.

A model is often used as a communication tool in these circumstances.

Traders like to use models where only one of the variables necessary to

determine the price of a product is not directly observable in the market.

The model then provides a one-to-one mapping of the product's price to

Business Snapshot 15.2 Exploiting the Weaknesses of a

Competitor's Model

A LIBOR-in-arrears swap is an interest rate swap where the floating interest

rate is paid on the day it is observed, not one accrual period later. Whereas a

plain vanilla swap is correctly valued by assuming that future rates will be

today's forward rates, a LIBOR-in-arrears swap should be valued on the

assumption that the future rate is today's forward interest rate plus a "convexity

adjustment".

In the mid-1990s sophisticated financial institutions understood the correct

approach for valuing a LIBOR-in-arrears swap. Less sophisticated financial

institutions used the naive "assume forward rates will be realized" approach

The result was that by choosing trades judiciously sophisticated financial

institutions were able to make substantial profits at the expense of their less

sophisticated counterparts.

The derivatives business is one where traders do not hesitate to exploit the

weaknesses of their competitor's models!

Model Risk and Liquidity Risk

347

the variable and vice versa. The Black-Scholes model (see Appendix C) is a

case in point. The only unobservable variable in the model is the volatility

of the underlying asset. The model therefore provides a one-to-one map-

ping of option prices to volatilities and vice versa. As explained in Chapter

5, the volatility calculated from the market price is known as the implied

volatility. Traders frequently quote implied volatilities rather than the

dollar prices. The reason is that the implied volatility is more stable than

the price. For example, when the underlying asset price or the interest rate

changes, there is likely to be a much bigger percentage jump in the dollar

price of an option than in its implied volatility.

Consider again the index option that has a mid-market price of

$30.50. Suppose it is a one-year European call option where the strike

price is 1,000, the one-year forward price of the index is 1,100, and the

one-year risk-free interest rate is 3%. The mid-market implied volatility

would be quoted as 15.37%.

The bid-offer spread might be "bid

15.24%, offer 15.50%".

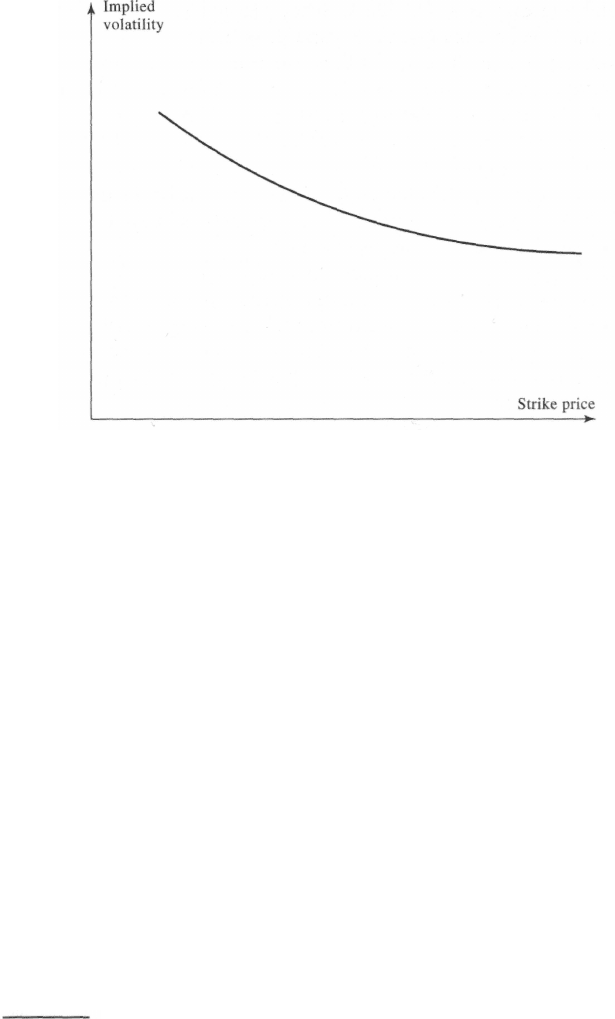
Volatility Smiles

The volatility implied by Black-Scholes (or by a binomial tree calcula-

tion such as that in Appendix D) as a function of the strike price for a

particular option maturity is known as a volatility smile.

If traders really

believed the assumptions underlying the Black-Scholes model, the

Figure 15.1 Volatility smile for foreign currency options.

Implied volatility calculations can be done with the DerivaGem software available on

the author's website.

It can be shown that the relationship between strike price and implied volatility should

be exactly the same for calls and puts in the case of European options and approximately

the same in the case of American options.

348 Chapter 15

Figure 15.2 Volatility smile for equity options.

implied volatility would be the same for all options and the volatility

smile would be flat. In fact, this is rarely the case.

The volatility smile used by traders to price foreign currency options

has the general form shown in Figure 15.1. The volatility is relatively low

for at-the-money options. It becomes progressively higher as an option

moves either in the money or out of the money. The reason for the

volatility smile is that Black-Scholes assumes

1. The volatility of the asset is constant.

2. The price of the asset changes smoothly with no jumps.

In practice, neither of these conditions is satisfied for an exchange rate. The

volatility of an exchange rate is far from constant, and exchange rates

frequently exhibit jumps.

It turns out that the effect of both a nonconstant

volatility and jumps is that extreme outcomes become more likely. This

leads to the volatility smile in Figure 15.1.

The volatility smile used by traders to price equity options (both those

on individual stocks and those on stock indices) has the general form

shown in Figure 15.2. This is sometimes referred to as a volatility skew. The

Often the jumps are in response to the actions of central banks.

Model Risk and Liquidity Risk 349

volatility decreases as the strike price increases. The volatility used to price

a low-strike-price option (i.e., a deep-out-of-the-money put or a deep-in-

the-money call) is significantly higher than that used to price a high-strike-

price option (i.e., a deep-in-the-money put or a deep-out-of-the-money

call). One possible explanation for the smile in equity options concerns

leverage. As a company's equity declines in value, the company's leverage

increases. This means that the equity becomes more risky and its volatility

increases. As a company's equity increases in value, leverage decreases.

The equity then becomes less risky and its volatility decreases. This

argument shows that we can expect the volatility of equity to be a

decreasing function of price and is consistent with Figure 15.2. Another

explanation is Crashophobia (see Business Snapshot 15.3).

Volatility smiles and skews such as those shown in Figures 15.1 and 15.2

are liable to change on a daily basis. This means that the volatilities

traders use change from day to day as well as from option to option. Why

does the market continue to use Black-Scholes (and its extensions) when

it provides such a poor fit to market prices? The answer is that traders like

the model. They find it easy to use and easy to understand.

Volatility Surfaces

Figures 15.1 and 15.2 are for options with a particular maturity. Traders

like to combine the volatility smiles for different maturities into a volatility

surface. This shows implied volatility as a function of both strike price

and time to maturity. Table 15.1 gives a typical volatility surface for

currency options. The table indicates that the volatility smile becomes less

Business Snapshot 15.3 Crashophobia

It is interesting that the pattern in Figure 15.2 for equities has existed only

since the stock market crash of October 1987. Prior to October 1987 implied

volatilities were much less dependent on strike price. This has led Mark

Rubinstein to suggest that one reason for the equity volatility smile may be

"Crashophobia". Traders are concerned about the possibility of another crash

similar to October 1987 and assign relatively high prices (and therefore

relatively high implied volatilities) for deep-out-of-the-money puts.

There is some empirical support for this explanation. Declines in the

S&P 500 tend to be accompanied by a steepening of the volatility skew,

perhaps because traders become more nervous about the possibility of a crash.

When the S&P increases, the skew tends to become less steep.

350 Chapter 15

Table 15.1 Volatility surface.

Time to

maturity

1 month

3 month

6 month

1 year

2 year

5 year

Strike price

0.90

14.2

14.0

14.1

14.7

15.0

14.8

0.95

13.0

13.3

14.0

14.4

14.6

1.00

12.0

12.5

13.5

14.0

14.4

1.05

13.1

13.4

14.0

14.5

14.7

1.10

14.5

14.2

14.3

14.8

15.1

15.0

pronounced as the time to maturity increases. This is what is usually

observed in practice.

The volatility surface is produced primarily from information provided

by brokers. Brokers are in the business of bringing buyers and sellers

together in the over-the-counter market and have more information on

the implied volatilities at which transactions are being done on any given

day than individual derivatives dealers. Over time an options trader

develops an understanding of what the volatility surface for a particular

underlying asset should look like.

To value a new option, traders look up the appropriate volatility in the

table using interpolation. For example, to value a 9-month option with a

strike price of 1.05, a trader would interpolate between 13.4 and 14.0 in

Table 15.1 to obtain a volatility of 13.7%. This is the volatility that would

be used in a Black-Scholes formula or a binomial tree calculation. When

valuing a 1.5-year option with a strike price of 0.925, a two-dimensional

interpolation would be used to give an implied volatility of 14.525%.

Hedging

It should be clear from the above discussion that models play a relatively

minor role in the pricing of actively traded products. Dealers interpolate

between prices observed in the market. A model such as Black-Scholes is

nothing more than a tool to facilitate the interpolation. It is easier to

interpolate between implied volatilities than between dollar prices.

If T is the time to maturity and F

is the forward price of the asset, some traders choose

to define the volatility smile as the relationship between implied volatility and

rather than as the relationship between the implied volatility and K. The smile is

usually much less dependent on the time to maturity.

Model Risk and Liquidity Risk 351

Models are used in a more significant way when it comes to hedging.

Traders must manage their exposure to delta, gamma, vega, etc. (see

Chapter 3). We can distinguish between within-model hedging and

outside-model hedging. Within-model hedging is designed to deal with

the risk of changes in variables that are assumed to be uncertain by the

model. Outside-model hedging deals with the risk of changes in variables

that are assumed to be constant (or deterministic) by the model. When

Black-Scholes is used, hedging against movements in the underlying stock

price (delta and gamma hedging) is within-model hedging because the

model assumes that stock price changes are uncertain. However, hedging

against volatility (vega hedging) is outside-model hedging because the

model assumes that volatility is constant.

In practice, traders almost invariably do outside-model hedging as well

as within-model hedging. This is because, as we have explained, the

calibration process causes parameters such as volatilities to change daily.

A natural assumption is that if hedging is implemented for all the

variables that could change in a day (both those that are assumed to

be constant by the model and those that are assumed to be stochastic) the

value of hedger's position will not change. In fact, this is not necessarily

the case. If the model used to calculate the hedge is wrong, then there may

be an unexpected gain or loss. The good news here is that on average the

gain or loss from hedging using the wrong model is approximately zero.

The risk of imperfect hedging is likely to be largely diversified away across

the portfolio of a large financial institution.

Many financial institutions carefully evaluate the effectiveness of their

hedging. They find it revealing to decompose the day-to-day change in a

portfolio's value into the following:

1. A change resulting from risks that were unhedged

2. A change resulting from the hedging model being imperfect

3. A change resulting from new trades done during the day

This is sometimes referred to as a P&L decomposition.

15.4 MODELS FOR STRUCTURED PRODUCTS

Exotic options and other nonstandard products that are tailored to the

needs of clients are referred to as structured products. Usually they do not

trade actively and a financial institution must rely on a model to deter-

mine the price it charges the client. Note the important difference between

352

Chapter 15

structured products and actively traded products. When a product trades

actively, there is very little uncertainty about its price and the model

affects only hedge performance. In the case of structured products, model

risk is much greater because there is the potential for both pricing and

hedging being incorrect.

A financial institution should not rely on a single model for pricing

structured products. Instead it should, whenever possible, use several

different models. This leads to a price range for the instrument and a

better understanding of the model risks being taken.

Suppose that three different models give prices of $6 million, $7.5 million

and $8.5 million for a particular product that a financial institution is

planning to sell to a client. Even if the financial institution believes that the

first model is the best one and plans to use that model as its standard model

for daily repricing and hedging, it should ensure that the price it charges

the client is at least $8.5 million. Moreover, it should be conservative about

recognizing profits. If the product is sold for $9 million, it is tempting to

recognize an immediate profit of $3 million ($9 million less the believed-to-

be-accurate price of $6 million). However, this is overly aggressive. A

better, more conservative, practice is to put the $3 million into a reserve

account and transfer it to profits slowly during the life of the product.

Most large financial institutions have model audit groups as part of

their risk management teams. These groups are responsible for vetting

new models proposed by traders for particular products. A model cannot

usually be used until the model audit group has approved it. Vetting

typically includes (a) checking that a model has been correctly imple-

mented, (b) examining whether there is a sound rationale for the model,

task, (d) specifying the limitations of the model, and (e) assessing

uncertainties in the prices and hedge parameters given by the model.

15.5 DANGERS IN MODEL BUILDING

The art of model building is to capture what is important for valuing

and hedging an instrument without making the model more complex

than it needs to be. Sometimes models have to be quite complex to

capture the important features of a product, but this is not always

the case.

This is also likely to have sensible implications for the way bonuses are paid.