Hooke R.L. Principles of glacier mechanics
Подождите немного. Документ загружается.


Collapse of a cylindrical hole 321
through (12.16). The resulting equations are:
σ
rr
= P
a
r
2/n
− P = P
a
r
2/n
− 1
(12.17a)
σ
θθ
= P
n − 2
n
a
r
2/n
− P = P
n − 2
n
a
r
2/n
− 1
(12.17b)
σ
zz
= P
n − 1
n
a
r
2/n
− P = P
n − 1
n
a
r
2/n
− 1
(12.17c)
σ =
1
2
(
σ
rr
− σ
θθ
)
=
P
n
a
r
2/n
(12.17d)
and the mean stress is
1
3
σ
kk
=
P
3
a
r
2/n
− 1 +
n−2
n
a
r
2/n
− 1 +
n−1
n
a
r
2/n
− 1
= P
n−1
n
a
r
2/n
− 1
(12.18)
Now, the stress causing closure is no longer a hypothetical traction on
the inside of the hole, σ
a
. Rather it is the real hydrostatic stress in the
medium. Note that all of the stresses decrease to −P (i.e. compressive)
at large distances from the hole.
It is easy to show that the corresponding deviatoric stresses are:
σ
rr
=−σ
θθ
=
P
n
a
r
2/n
(12.19a)
σ
zz
= 0 (12.19b)
That σ
rr
=−σ
θθ
and σ
zz
= 0 are a consequence of our assumption of
plane strain.
Setting r =a in Equations (12.17) we obtain the stresses on the hole
wall:
σ
rr
=0
σ
θθ
=−
2P
n
σ
zz
=−
P
n
σ =
P
n
(12.20)
Tunnel and borehole closure
These relations have been used to determine values of the constants
n and B in the flow law with the use of measurements of the rate of
closure of a tunnel or borehole. To do this, it is necessary to incorporate

322 Applications of stress and deformation principles
the relations into the flow law. Deviatoric stresses are thus required.
Because we are interested in closure, only σ
rr(r=a)
is needed. Thus, using
Equation (12.19a) with r =a, noting that σ
r=a
= P /n, and remembering
Equations (9.29) and (10.39):
˙ε
rr(r=a)
=
σ
n−1
B
n
σ
rr(r=a)
=
P
!
n
n−1
B
n
P
n
(12.21)
Because ˙ε
rr(r = a)
=−u
a
/a, where u
a
is the closure rate, we obtain
−
u
a
a
=
P
nB
n
(12.22)
To use Equation (12.22)toestimate the constants in the flow law,
one needs values of u
a
, a, and P at two or more places. Inserting values
for two such places in Equation (12.22)would yield two equations with
two unknowns (n and B). With three or more sets of data, it is useful to
plot log ˙ε against log P as is done for some tunnel-closure experiments
in Figure 12.4.
Some caution is required, however. In tunnel-closure studies, for
example, pegs are normally inserted in the tunnel walls and closure is
measured by determining the change in distance between the heads of
pegs on opposite sides of the tunnel. In this case, particularly in temperate
glaciers, the point where the pegs are actually gripped by the ice may
be some distance back in the wall. Furthermore, such tunnels are rarely
if ever circular in cross section. Thus the correct value of a must be
guessed.
In borehole-closure studies, closure rates are measured with calipers,
so determining the appropriate value of a is not a problem. However, the
time interval between measurements is often fairly large, and a substan-
tial amount of closure may occur between measurements. In this case,
approximating u
a
by a/t is likely to yield a poor estimate (Paterson,
1977). The correct procedure is to use the temporal mean value of u
a
/a,
which is, by the definition of a mean:
˙ε
a
=−
1
t
t
2
t
1
u
a
a
dt
Noting that u
a
= da/dt, this becomes:
˙ε
a
=−
1
t
t
2
t
1
1
a
da
dt
dt =−
1
t
ln
a
2
a
1
Some results from four borehole closure studies are presented in Figure
12.5 (open circles) along with data on the variation of B with temperature
from a large number of other laboratory and field experiments.
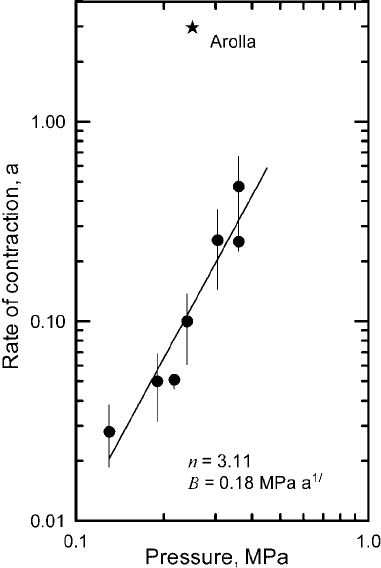
Collapse of a cylindrical hole 323
−1
n
Figure 12.4. Rate of
contraction, u
a
,oftunnel
sections plotted against
overburden pressure, P
(Replotted from Nye, 1953,
Figure 1. Reproduced with
permission of the author and
The Royal Society of London.)
It is instructive to look at the results in Figures 12.4 and 12.5 in
somewhat greater detail. In Figure 12.4,itwill be noted that several
of the sets of tunnel closure data fall along a line with n = 3.11 and
B = 0.18 MPa a
1/n
. This value of B is plotted as the open square in
Figure 12.5;itisquite consistent with other data from temperate ice.
However, the point representing data from the Arolla ice tunnel falls
well above the line in Figure 12.4. The Arolla tunnel is at the base of
an ice fall. Owing to the contribution of longitudinal stresses, σ may
be significantly higher than P/n here, and, as observed, one would thus
expect the actual closure rate to be higher than that calculated using
(P/n)
n−1
to approximate σ
n−1
in Equation (12.21).
The problem with the borehole-closure rates, which seem to be
too low and therefore yield values of B that appear to be too high in
Figure 12.5,isdifferent. Here, we speculate that the crystallographic
fabric in the ice is adjusted to a stress regime in which the dominant
deviatoric stress is simple shear normal to the axis of the hole. Such a
fabric may have inhibited closure.
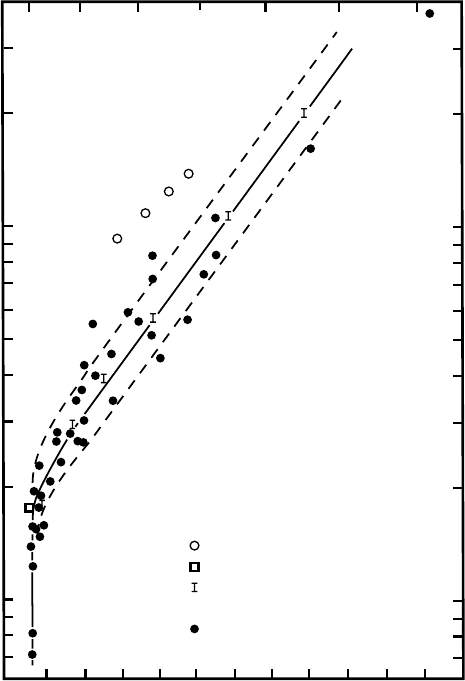
324 Applications of stress and deformation principles
B
, MPa a
1/3
0.5
1.0
4.0
0.1
0.06
3.6 4.0 4.4 4.8 x 10
−3
1/T, K
0 −30 −60
Temperature,
o
C
Borehole closure experiments
Tunnel closure (Nye, 1953)
Barnes
et al.
(1971) laboratory
experiments
Other data (see Hooke, 1981,
for sources)
Figure 12.5. Values of B from
various experiments in which
the minimum strain rate was
measured or estimated.
Octahedral stresses and strain
rates were used in calculating
B. Straight part of solid line is
based on data from Barnes
et al.(1971). Dashed lines are
values of B that would give
strain rates half or double
those on solid line. (After
Hooke, 1981, Figure 2).
Subglacial water conduits
In Chapter 8 we applied Equation (12.22)toclosure of subglacial water
conduits. As noted there, problems arise when one attempts to estimate
closure rates of semicircular conduits, owing to drag on the bed. Even
more profound difficulties arise in attempting to estimate closure rates
of broad low conduits, as stresses in the ice are no longer symmetrically
distributed about the conduit.
Here, we look into another problem of interest: the normal stresses
on the bed at the boundaries of a semicircular conduit, and in particular,
the gradient in these stresses outward from the conduit (Figure 12.6).
This problem was first studied by Weertman (1972). If pressures are

Collapse of a cylindrical hole 325
s
rr
s
qq
s
qq
s
qq
=
−
r = a
Bed
r
Ice
r
= R
n
> 2
n
=
2
n
<
2
P
Figure 12.6. Stresses around
a semicircular conduit: σ
rr
is
extending and σ
θθ
is
compressive (hence the minus
sign on P). The variation in
σ
θθ
away from the tunnel is
shown schematically. For
n > 2, σ
θθ
is less compressive
than P, and conversely.
higher adjacent to the conduit, water in a film at the ice–bed interface
will be forced away from the conduit, and conversely.
The significance of this problem lies in its application to water flow
beneath polar ice sheets. Several authors have suggested that for conduits
to exist beneath such ice masses in the absence of water inputs from the
glacier surface, there must be an influx of water from adjacent parts of the
bed (Alley, 1989a;Walder, 1982;Weertman and Birchfield, 1983; Ng,
2000a). The problem of the existence of such conduits is fundamental;
where they are present, subglacial water pressures are probably appre-
ciably lower than otherwise. Thus, any attempt to explain, for example,
the fast flow of ice streams hinges upon an understanding of the nature
of the water flow system.
The relevant stress in this problem is σ
θθ
. Thus, let us start with
the expression for σ
θθ
in Equation (12.14a). Note that in so doing, we
tacitly assume that the bed is flat and slippery so that shear stresses do
not impede movement of ice inward toward the tunnel. The appropriate
value for σ
a
is now the difference between the pressure in the ice and
that in the water in the conduit, P.Asbefore, we add a pressure, −P,
everywhere to account for the weight of the ice. With a little rearranging,
Equation (12.14a) thus becomes:
σ
θθ
=
n − 2
n
Pa
2
n
r
−
2
n
− P (12.14b)
Note that σ
θθ
is negative, or compressive, as P always exceeds the first
term on the right.
It may appear from Equation (12.14b) that σ
θθ
will not support the
weight of the glacier when n > 2, as then σ
θθ
→−P as r →∞but

326 Applications of stress and deformation principles
σ
θθ
> −P near the conduit. In other words, σ
θθ
is sufficiently compres-
sive to support the glacier far from the conduit but not near or beneath it.
However, σ
(rr = R)
is more compressive than σ
(rr = a)
(Equation (12.17a)),
and this provides the additional support. In other words, referring to Fig-
ure 12.6, the vertical force acting on the surface at radius R balances that
on the bed, which is: 2
∫
a
0
(P − P)dr + 2
∫
R
a
(
σ
θθ
−P) dr.
Let us now consider a semicircular conduit at a depth h
o
on a horizon-
tal bed beneath an ice sheet of uniform thickness and infinite horizontal
extent. Taking the derivative of σ
θθ
with respect to r along the bed yields
dσ
θθ
dr
=−
2
n
n − 2
n
Pa
2
n
r
−
(
2
n
+1
)
(12.23)
If n > 2, as might be expected, dσ
θθ
/dris negative. Thus σ
θθ
decreases,
or becomes more negative, or more compressive, away from the tunnel
(Figure 12.6). In this case, water in a film will be forced toward the con-
duit, enhancing discharge in it. However, when one considers coupling
of stresses, particularly where there is a shear stress on the bed parallel
to the conduit, the situation is not so simple. It appears that in this case
water flow may be away from the tunnel (Weertman, 1972, pp. 299–300).
The physical reason for the change in behavior of dσ
θθ
/dr with n is
not obvious. We might expect that if a cavity is introduced at the base
of a glacier, compressive stresses adjacent to the cavity would increase
in order to support that part of the weight of the glacier that is no longer
supported by the bed under the cavity. However, toward the tunnel u,
and hence ˙ε
rr
, increase and this requires an increase in σ
rr
. The way in
which the stress field is modified to satisfy this requirement, and hence
the way in which the pressure on the bed is redistributed, depends upon
n.Amore intuitive explanation of this effect is elusive.
Calculating basal shear stresses using
a force balance
Toafirst approximation, the basal drag can be estimated from τ
b
=ρghα
(or τ
b
= S
f
ρghα in a valley glacier). However, if longitudinal forces are
unbalanced, τ
b
may be either greater or less than ρghα.For example, in
Figure 12.7, the body force, ρgh, has a downslope component, ρghα.In
addition, there are longitudinal forces F
u
and F
d
.IfF
u
> F
d
,assuggested
by the lengths of the arrows in the figure, τ
b
will clearly have to be
greater than ρghα in order to balance forces parallel to the bed, and
conversely. We now explore this effect in greater detail. The first part of
the development is a three-dimensional generalization of an approach
suggested by B. Hanson (Hooke and Hanson, 1986,p.268).

Calculating basal shear stresses 327
F
u
F
d
a
t
b
rgha
rgh
Figure 12.7. Longitudinal
forces on a segment of a
glacier on a sloping bed. If
F
u
> F
d
the basal drag will be
greater than ρghα, and
conversely.
bed
surface
h
y
z
x
Figure 12.8. Coordinate
system used in force balance
analysis.
Because our goal is to calculate the drag exerted on the glacier by
the bed, the momentum balance equations (Equations (9.32b)) are the
obvious starting point for the analysis. The coordinate system to be used
is shown in Figure 12.8. The x-axis is horizontal and in the direction
of flow, and the z-axis is vertical. Writing out the momentum balance
equations in the x- and z-directions, remembering that σ
ij
= σ
ij
– δ
ij
P,
leads to:
∂σ
xx
∂x
+
∂σ
yx
∂y
+
∂σ
zx
∂z
+
∂ P
∂x
= 0 (12.24a)
and
∂σ
xz
∂x
+
∂σ
yz
∂y
+
∂σ
zz
∂z
+
∂ P
∂z
=−ρg (12.24b)
The procedure now will be to solve Equation (12.24b) for P, substitute
the result into Equation (12.24a), and integrate over the depth to obtain
σ
zx(z=h)
(= τ
b
).
To solve Equation (12.24b) for P, separate variables and integrate
over depth z:
z
0
dP =−
z
0
∂σ
xz
∂x
dz −
z
0
∂σ
yz
∂y
dz −
z
0
dσ
zz
−
z
0
ρgdz
or, noting that P = 0atthe surface:
P =−
z
0
∂σ
xz
∂x
dz −
z
0
∂σ
yz
∂y
dz − σ
zz
+ σ
zz
|
z=0
− ρgz

328 Applications of stress and deformation principles
Now take the horizontal derivative, assuming that ∂σ
zz
/∂x|
z=0
is negli-
gible and noting that dz/dx = α, and substitute the result into Equation
(12.24a), thus:
∂σ
xx
∂x
+
∂σ
yx
∂y
+
∂σ
zx
∂z
−
z
0
∂
2
σ
xz
∂x
2
dz −
z
0
∂
2
σ
yz
∂x∂ y
dz −
∂σ
zz
∂x
− ρgα = 0
(12.25)
Equation (12.25)isinterms of stresses at any given level, z,inthe glacier,
whereas we are interested in summing the stresses over depth to obtain
τ
b
. Thus, as just noted, we integrate over depth:
h
0
∂σ
xx
∂x
−
∂σ
zz
∂x
dz +
h
0
∂σ
yx
∂y
dz +
h
0
dσ
zx
−
h
0
z
0
∂
2
σ
xz
∂x
2
+
∂
2
σ
yz
∂x∂ y
dz dz − ρghα = 0 (12.26)
Clearly, σ
zx (z=h)
(= τ
b
) will be obtained from integrating the third term,
and the last term is the familiar ρghα. Some simplification is obviously
desirable, however.
The double integral term in Equation (12.26), also sometimes
referred to as the T-term, is difficult to interpret physically. In two dimen-
sions, Budd (1969,p.116) has shown that it can be approximated by:
h
0
z
0
∂
2
σ
xz
∂x
2
dz dz
∼
=
1
6
ρg
∂
2
∂x
2
(αh
3
)
(12.27)
Van der Veen and Whillans (1989)argue that this term is related to
“bridging” effects, in which the pressure on the bed varies spatially owing
to the influence of bed irregularities and, particularly, cavity formation.
Because ice is “soft”, they suggest that these bridging effects should be
small compared with the average normal pressure. Thus, they neglect the
T-term in force-balance calculations, and we shall follow their lead in this
respect. They acknowledge, however, that the “physical implications” of
doing so are “not conceptually straightforward”.
Tur ning to the first term in Equation (12.26), σ
zz
can be eliminated
by noting that, owing to the proportionality between deviatoric stress
and strain rate, the incompressibility condition, ˙ε
xx
+ ˙ε
yy
+ ˙ε
zz
= 0, leads
to σ
xx
+ σ
yy
+ σ
zz
= 0. In addition, because σ
zx
would be zero on a free
horizontal surface, and is only slightly different from zero on the gently
sloping glacier surface, the third term in Equation (12.26)isthe desired
basal drag, τ
b
,asjust noted. With these modifications, Equation (12.26)

Calculating basal shear stresses 329
becomes:
h
0
∂
∂x
2σ
xx
+ σ
yy
dz +
h
0
∂σ
yx
∂y
dz + τ
b
−ρghα = 0 (12.28)
To get an intuitive sense for this relation, consider a situation in which
σ
xx
and σ
yx
are independent of depth and σ
yy
is negligible. Then Equation
(12.28) reduces to:
ρghα − τ
b
= 2
∂σ
xx
∂x
h +
∂σ
yx
∂y
h (12.28a)
In two dimensions (σ
yx
= 0), this equation says that if the driving stress,
ρghα,exceeds the drag provided by the bed, τ
b
, the stretching rate
(˙ε
xx
∝ σ
xx
) will increase downglacier (∂σ
xx
/∂x > 0), and conversely.
The second term on the right takes shear stresses on the valley sides into
consideration. (Adjusting for the fact the we have neglected bridging
effects and have taken the z-direction to be positive downward, Equation
(12.28)isidentical to Van der Veen and Whillans’ (1989) Equation
(12.25). The rest of our development follows theirs.)
Our objective now is to express Equation (12.28)inaform that
will allow evaluation of τ
b
from strain rate measurements at the glacier
surface. To this end, we note that because
σ
n−1
= (˙ε
1
n
B)
n−1
the flow law can be written:
˙ε
ij
=
σ
n−1
B
n
σ
ij
=
˙ε
n−1
n
B
σ
ij
Inserting this in Equation (12.28), reversing the order of differentiation
and integration, and rearranging terms yields:
τ
b
= ρghα −
∂
∂x
h
0
B
˙ε
n−1
n
(2˙ε
xx
+ ˙ε
yy
)dz −
∂
∂y
h
0
B
˙ε
n−1
n
˙ε
yx
dz (12.29)
Van der Veen and Whillans (1989)developed a numerical procedure
to carry out the integration over depth, z.However, for simple applica-
tions we assume that strain rates are independent of depth, and express
Equation (12.29)infinite-difference form, thus:
τ
b
= ρghα − B ˙ε
1−n
n
(2˙ε
xx
+ ˙ε
yy
)h
"
"
dwn
− (2˙ε
xx
+ ˙ε
yy
)h
"
"
up
x
− B ˙ε
1−n
n
˙ε
yx
h
"
"
rgt
− ˙ε
yx
h
|
lft
y
(12.30)
Here, the symbols |
dwn
, |
up
, |
rgt
, and |
lft
refer, respectively, to the
downglacier and upglacier ends, and to the left and right sides (look-
ing downglacier), of a “block” of the glacier of length x and width y.

330 Applications of stress and deformation principles
Table 12.1. Force balance calculations
Time ˙ε
xx
(up), a
−1
˙ε
xx
(dwn), a
−1
Term 2
*
,kPa Term3
*
,kPa τ
b
,kPa τ
b
,%
Block A
Winter −0.016 −0.004 1 −34 −82 —
July 1983 0.001 −0.005 −25 −38 −52 −37
July 1983 −0.006 −0.011 −17 −36 −62 −24
May 1984 −0.008 −0.018 −19 −38 −58 −29
June 1984 0.001 −0.002 −26 −40 −49 −40
June 1985 −0.010 −0.007 −7 −38 −69 −16
Block B
Winter 0.006 −0.008 −28 −25 −92 —
July 1983 Data incomplete
July 1983 Data incomplete
May 1984 0.000 −0.053 −23 −31 −91 −1
June 1984 −0.002 0.037 40 −15 −170 +84
June 1985 −0.002 −0.002 9 −25 −129 +40
The values of ρghα were 115 kPa beneath block A and 145 kPa beneath block B.
*
Terms2and 3 are the second and third terms on the right-hand side of Equation (12.30), the longitudinal and
transverse terms, respectively.
The second term on the right represents the contribution to τ
b
of an
imbalance in forces on the ends of the block, while the third represents
the contribution of forces on the sides.
An example of an application of this procedure is provided by an
experiment conducted on Storglaci¨aren, Sweden (Hooke et al., 1989).
Some stakes on the glacier surface (Figure 12.9)were surveyed fre-
quently between 1982 and 1985 to determine velocities (Figure 12.10).
The pattern of stakes was such that longitudinal and transverse strain
rates could be calculated at the upglacier and downglacier ends of the
“blocks” labeled A and B in Figure 12.9, and shear strain rates could be
calculated along the sides. Results of the calculations for six time periods
are shown in Table 12.1. One time period represents mean winter condi-
tions; τ
b
was then −82 kPa beneath block A and −92 kPa beneath block
B. The other five time periods were those during which high velocity
events occurred (Figure 12.10). During these events, τ
b
was reduced an
average of nearly 30% beneath block A. Beneath block B the change
in τ
b
was more variable, but significant increases occurred during two
events.
Study of the patterns of changes suggests that acceleration of block
A was, in every case, accompanied by an increase in magnitude of
