Hooke R.L. Principles of glacier mechanics

Подождите немного. Документ загружается.

Types of subglacial drainage system 221

previous year’s tunnel system, maintained by the small winter discharge

provided by subglacial melt, are likely to survive. These conduits will

increase in size rapidly as water inputs increase in the spring. This is

because the water backs up in the undersized conduit system, resulting

in high potential gradients and hence high melt rates on conduit walls,

and also high pressures that inhibit closure. If such remnant tunnels do

not exist, or if they do not enlarge rapidly enough, the water pressure may

rise to the level where Kamb’s stability limit for the linked cavity system

is exceeded. New tunnels may then form by growth and coalescence of

links. In either case, water pressures drop abruptly as the tunnel system

is reestablished. Measurements of seasonal variations in water pressure

(Hooke et al., 1989), of dye dispersion (Seaberg et al., 1988; Hock and

Hooke, 1993), and of surface velocity (Hodge, 1974; Hooke et al., 1989)

lend strong support to this model.

A reasonable supposition is that the linked-cavity and tunnel models

represent end members of a continuum of drainage types. The drainage

system beneath fast-moving glaciers, including those that are surging

(discussed below), may be near the linked-cavity end member in this

continuum. Conversely, ice sheets that are nearing stagnation, and thus

beneath which there is little separation and cavity formation, may have

drainage systems approximating the tunnel end member.

Multi-branched arborescent system

A conduit system that has some of the characteristics of both the tun-

nel and the linked-cavity systems is one that consists of an arborescent

network of broad, low conduits, each of which is individually braided

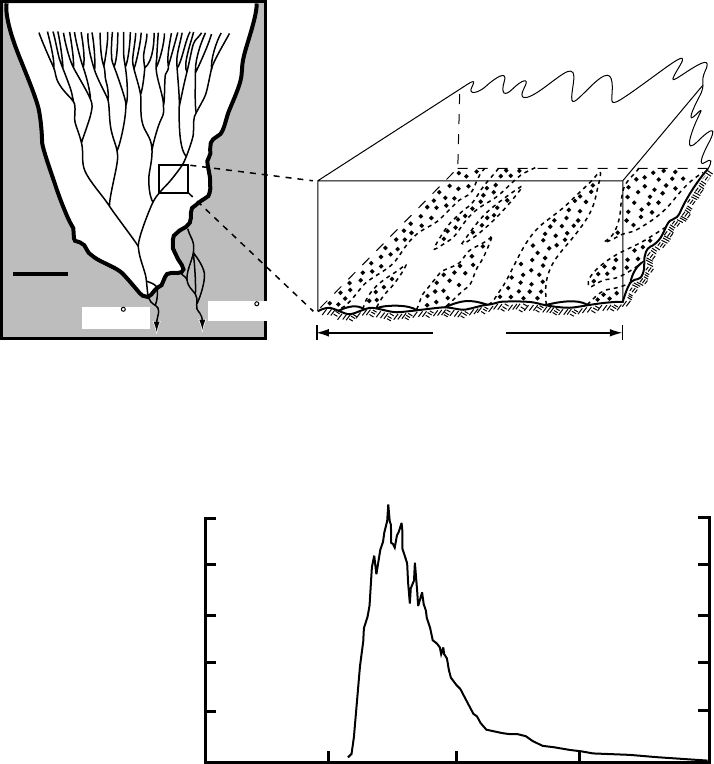
(Figure 8.18). Hock and Hooke (1993) called this a multi-branched

arborescent system. They envisaged subglacial streams ﬂowing in tun-

nels that are, in comparison with the linked-cavity system, relatively

straight and uniform in size. As in the linked-cavity system, it is specif-

ically recognized that no part of the glacier bed should be far from a

conduit.

Hock and Hooke developed the idea of the multi-branched arbores-

cent system from tracer studies on Storglaci¨aren. Dye was injected into a

moulin about a kilometer from the terminus, and its arrival in one of the

two streams draining the glacier, Sydj˚akk (Figure 8.18a), was recorded.

As is commonly observed in tracer studies, the water velocities obtained

from these tests were too low to be consistent with the existence of

a single large tunnel from the moulin to the terminus. However, the

velocities could be modeled rather well by assuming that the drainage

system bifurcated several times between the terminus and the moulin,

so that each of the highest tributaries of the system carries an average of

222 Water ﬂow in and under glaciers

Sydjakk

Nordjakk

0 200m

Ice

. 5 m

(b)(a)

Figure 8.18. Schematic sketches (a) of the multi-branched arborescent conduit

system postulated to exist beneath Storglaci

aren, and (b) of an individual

braided channel in the system. (After Hock and Hooke, 1993, Figures 4 and 6.)

Dye concentration,

mg m

−3

−1

500

420

Hours since injection

Figure 8.19. Typical dye-return curve from a test on Storglaci

aren. Ordinate is

milligrams of dye per cubic meter of water and kilogram of dye injected. (From

Hock and Hooke, 1993, Figure 3.)

only ∼3% of the discharge at the terminus (Figure 8.18a). This model

is also consistent with the observation that there are many small streams

and moulins at this location on the glacier, implying many sources.

That the individual channels are braided (Figure 8.18b)issuggested

by multiple peaks in some of the dye-return curves (Figure 8.19). Such

peaks occur when dye following one anabranch of a braided system

moves more slowly than that in another anabranch. The two packages of

dye then reach the terminus at different times.

Types of subglacial drainage system 223

The multi-branched arborescent model is consistent with two basic

observations: (1) that measured water velocities are much lower than they

would be in a single conduit; and (2) that water pressures are relatively

uniform over the bed, as observed by Iken and Bindschadler (1986)on

Findelengletscher. The uniform drainage for all parts of the glacier bed

provided by the multi-branched arborescent system should result in such

relatively uniform water pressures. It is likely, however, that many of the

smaller tributaries providing this uniform drainage are actually linked

cavities.

As noted (Figure 8.13), winter water pressures beneath Storglaci¨aren

have been modeled rather well with the use of R¨othlisberger’s theory

modiﬁed to reﬂect, approximately, the wide shallow geometry of the

channels. Thus, in contrast to the situation in a linked-cavity system, it

seems likely that steady-state water pressures in the wide shallow chan-

nels that characterize the multi-branched arborescent system decrease

with increasing discharge.

Even within the framework of the multi-branched arborescent model,

however, there can be appreciable differences among nearby glaciers.

Iken and Bindschadler (1986,p.110), for example, used electrical con-

ductivity measurements in proglacial streams and other observations

to study the differences between the subglacial drainage of Findelen-

gletscher and Gornergletscher. These two glaciers are both near Zermatt

in the Swiss Alps and are of comparable size. They concluded that the

drainage of Gornergletscher was in a few large tunnels, whereas that of

Findelengletscher was in a larger number of smaller conduits. They did

not propose an explanation for this difference.

Conduits on deforming till

Heretofore, our discussion of subglacial conduits has focused on situ-

ations in which the bed was comparatively rigid. Many glaciers, how-

ever, move over beds of deformable till. In Chapter 7 we found that

the deformability of till and the nature of the coupling between it and

the glacier sole are both strongly dependent upon the effective pressure,

− P

.Inturn, the effective pressure depends, through P

,onthe

nature of the drainage system at the ice–till interface. As P

at such

an interface is clearly of prime importance in the development of ice

streams and also in surging by a mechanism proposed by Truffer et al.

(2000), a quantitative understanding of conduits on deformable sub-

strates is clearly needed.

As with a conduit at an ice–rock interface, the roof of a conduit at an

ice–till interface also tends to close when P

< P

, and in the steady state

this tendency is balanced by melting. In addition, however, creep of till

into the conduit may tend to constrict it, and in the steady state any such

224 Water ﬂow in and under glaciers

Figure 8.20. Possible geometry of a subglacial conduit incised into till. Vectors

are based on Ng (2000b, Figure 9) and show approximate transverse velocity

distribution in the ice and in the till for a situation in which the effective viscosity

of the till is substantially less than that of the ice (see text). Some vectors on the

right are omitted for clarity.

ﬂow must be balanced by erosion of the till by the ﬂowing water (Alley,

1989a;Walder and Fowler, 1994; Ng, 2000a, b). The physics of the latter

processes are still poorly understood, as neither the rheology of till nor

the mechanics of sediment transport are known well enough.

Nevertheless, we can make some predictions about the nature of

the drainage system. Consider the channel shown in Figure 8.20.Ifany

sediment on the sloping “bank” of the channel, as at A in Figure 8.20, can

be moved downstream by the current, gravitational forces will tend to

move it, also, toward the middle of the channel. Consequently, channels

should become wider and shallower until the velocity and shear stress

on the banks are too low to move sediment. Parker (1979) has proposed

that in the transition zone between the bed and the bank, lateral diffusion

of downstream momentum results in a gradual outward decrease in the

shear stress, τ

,exerted by the water on the bed, so that movement of

bed material actually decreases gradually toward the banks rather than

ceasing abruptly at some particular threshold depth. Although Parker’s

model was developed for subaerial gravel-bedded rivers, there is no

obvious reason why it should not also apply to subglacial conduits in

noncohesive till, even if the till is ﬁne grained, so long as there is an

inward-sloping bank region. Channels in till are thus likely to be wide and

shallow, as illustrated in Figure 8.20,aconclusion shared by Engelhardt

and Kamb (1997), Walder and Fowler (1994), and Ng (2000a, b).

Ng (1999) has suggested that in such a conduit, the vertical closure

rate, w, due to ﬂow of ice should be given approximately by:

w(y) =









− y

(8.26)

Types of subglacial drainage system 225

where  is the half width of the conduit, y is the distance from its center,

and the appropriate value for B is ∼ 0.16 MPa a

1/3

. Thus, w is highest in

the middle of the channel, at y =0, and decreases toward the bank, y = .

(w = 0aty=  for reasons described below.) This would be consistent

with the suggestion (Shreve, 1985a) that melt rates should be higher

where the water is deeper and the energy dissipation thus greater. Ng also

proposes a similar relation for creep of till into the conduit, with (P

/2B)

in Equation (8.26) replaced with an appropriate relation for till.

In Figure 8.20, w = 0aty=  because the till layer is of ﬁnite thick-

ness and removal of sediment creeping into the conduit results in thinning

of the till layer adjacent to the conduit. Thus, the ice–till boundary adja-

cent to the channel sinks, and vectors in the till are nearly horizontal.

In addition, the vectors in Figure 8.20 reﬂect a situation in which the

effective viscosity of the till is substantially less than that of the ice. If

the effective viscosities are roughly equal, ﬂow of the till is much slower,

owing in part to the limited thickness of the till (Ng, 2000b).

Let us now consider the water pressure in such a conduit. Walder

and Fowler (1994) note that a low water pressure will promote ﬂow of

ice toward a conduit but strengthen till. Under these conditions, they

argue that the channel bed may be relatively ﬂat, and the conduit will

be melted upward into the ice. Conversely, a high water pressure will

promote ﬂow of till into a conduit but inhibit inward ﬂow of ice. In this

case, the channel may tend to be cut downward into the till. Their analysis

suggests that the transition between these two regimes should occur at

an effective pressure of ∼ 0.8 MPa, but the uncertainty in this ﬁgure is

quite large.

Ice sheets tend to have relatively low surface slopes. Potential gra-

dients are thus low, so

m is low (Equation (8.12)). The conduit system

must then adjust to provide a high P

, thus inhibiting closure by ice ﬂow.

This may enhance deformation of till into conduits. Conversely, valley

glaciers normally have higher surface slopes, so

m will be higher and P

lower, perhaps leading to conduit geometries controlled by the inward

ﬂux of ice.

We have seen that in circular or semicircular conduits, P

decreases

as Q increases so water is diverted from smaller conduits to larger ones,

leading to an arborescent drainage network. Of interest, then, is the ques-

tion of whether this relation between P

and Q also holds for conduits

on deforming till.

Let us leave this question for the moment to describe an elegant

analysis by Ng (2000a)inwhich he derived three coupled ordinary dif-

ferential equations that could be solved numerically for the discharge,

Q, and sediment discharge, Q

,inaconduit, and the effective pressure,

, all as functions of distance along a conduit from its source. The

226 Water ﬂow in and under glaciers

principal independent variables in the analysis are the ﬂuxes of water

and sediment into the conduit. The water ﬂux is from basal melting over

some distance on either side of the conduit, and the sediment ﬂux is from

small tributaries along the conduit. The coupling among these variables

occurs because P

is a measure of: (1) the ﬂux of ice toward the conduit,

and thus of the contributions of melting of the conduit roof to Q, and

(2) the strength of the till and hence of the ﬂux of till into the bottom

of the conduit. Knowing these three parameters, Ng calculates , τ

m, d/ds, conduit height, h (Figure 8.20), mean water velocity,

u, and

mean sediment concentration,

c, subject to the constraints, expressed as

equations, that:

c = Q

/Q;

c is related to τ

and h because they determine the intensity of turbu-

lence;

is related to u and the hydraulic roughness of the conduit;

u times the cross-sectional area of the conduit must equal Q;

w, integrated across the conduit, must equal

m;

d/ds is related to the slope of the ice surface and to dP

/ds (Equation

(8.5)); and

m is related to d/ds and Q (Equation (8.12)).

Thus, there are seven equations and seven unknowns. Closure of the

conduit by ice ﬂow is assumed to be given by Equation (8.26) and closure

by ﬂow of till by a similar equation. Taken as constant in the solution are

sediment grain size, conduit roughness, and the slope of the ice surface.

In addition, energy used to keep the water at the pressure melting point

(Equation (8.10)) is neglected, so rigorously the solution applies only to

an ice sheet of uniform thickness. Particularly noteworthy in this solution

is the fact that conduit size and shape and the rate of erosion of the bed

are all determined solely by the independent variables – the water and

the sediment ﬂuxes from basal melting and small tributaries – together

with some parameters like grain size that are speciﬁed and held constant.

In an illustrative calculation based on this model, Ng assumed that a

small amount of water was seeping through the till and along the ice–till

interface upstream from the head of the conduit. This water entered the

conduit without transporting any sediment, so Q > 0butQ

= 0 here.

was taken to be 0.1 MPa at the head, well below the hypothesized

transition at ∼0.8 MPa. Along the conduit, basal melting was presumed

to supply water at a constant rate of 0.01 m

−1

, and the sediment

ﬂux from tributaries was taken to be 265 g s

−1

Downstream changes in several key variables are shown in Figure

8.21.Atthe upstream end of the conduit there is a boundary zone

about 30 km long in which dP

/ds = 0(Figure 8.21b), and  and h

vary somewhat erratically (Figure 8.21d); downstream from this zone,

Types of subglacial drainage system 227

Conduit height,

Sediment

concentration, g I

−1

Effective

pressure, MPa

Discharge,

−1

Erosion rate,

m a

−1

(a)

( )

−1

(b)

(c)

(d)

(e)

Figure 8.21. (a) Discharge and sediment load in a stream 100 km long

beneath an ice sheet of uniform thickness. (b) Effective pressure and

and (e) melt rate on the conduit roof and sediment ﬂux into conduit by till

creep. (Plotted from data kindly supplied by Felix Ng, some of which were used

in his 2000a paper.)

∝ Q

1/2

−5/6

which turns out to be essentially constant. The con-

tribution of roof melting (Figure 8.21e)toQ is negligible in compari-

son with the total Q so the discharge increases nearly linearly (Figure

8.21a). On the other hand, Q

increases nonlinearly (Figure 8.21a). This

is because

c also increases (Figure 8.21c), and Q

= cQ. The increase

c is a consequence of increases in both u and τ

in response to the

228 Water ﬂow in and under glaciers

increase in h (Figure 8.21d). As deduced earlier, h   (Figure 8.21e)

so the conduit is wide and low. Generally, dQ

/ds is substantially more

than the 265 g s

−1

supplied by tributaries. For example, 70 km

from the head of the conduit dQ

/ds ≈ 1800 g s

−1

. Thus the bulk

of the sediment load is supplied by erosion of till creeping into the con-

duit. Indeed, the rate of erosion of the conduit ﬂoor ranges from ∼2to

nearly 7 m a

−1

(Figure 8.21e). This is substantially higher than the melt

rate of ∼0.17 m a

−1

on the conduit roof.

In the foregoing analysis, the fact that P

∝ Q

−5/6

is particularly

important because this means that P

increases as Q increases and a

distributed drainage system with many wide low conduits like the one

in Figure 8.20 is to be expected. Field evidence also suggests that the

drainage is distributed when water pressures are high (or P

is low). On

Storglaci¨aren, Hooke and Pohjola (1994) found that in an area where

water pressures were uniformly high, neither dye-trace experiments nor

water pressure records gave any indication of channelized drainage along

the bed. Indeed, both the dye-trace studies and video observations of

the bed suggested a drainage system in which low conduits with high

aspect ratios were frequently opened and closed, resulting in episodic

movement of water from one pocket to another. Flow velocities were of

order 10

−2

−1

. These observations were made in an overdeepened

basin in which much of the viscous energy may have been needed to keep

the water at the pressure melting point. However, they are consistent with

observations in boreholes in West Antarctic ice streams (Engelhardt and

Kamb, 1997; Kamb, 2001). The holes were drilled with the use of a hot

water drill. During drilling, the water level in a hole is at the ice–ﬁrn

transition, but upon breakthrough to the bed, it falls rapidly until the

pressure exerted by the column of water in the hole equals the pressure

in the local subglacial hydraulic system. By measuring the rates at which

water levels fell, Engelhardt and Kamb calculated that a gap between the

ice and the bed that was only ∼2mmhigh would be sufﬁcient to account

for the observed rate of fall. Analysis of oscillations in water pressure in

nearby holes, interpreted as indicating seiche-like ﬂow back and forth

between the holes when the second hole reached the bed, also suggested

agap of this size (Kamb, 2001,p.187).

Engelhardt and Kamb made other observations that provide insight

into the nature of the drainage system beneath ice streams. In some holes,

water levels dropped more slowly or, rarely, not at all. This suggests

that the hole reached the ice–till interface at a place where gaps were

smaller or where there was no gap at or near the hole bottom. They also

observed that, upon breakthrough, the falling water level resulted in a

pressure pulse in other nearby holes on some occasions but not on others.

Over time spans of several months they noted that water levels ﬂuctuated

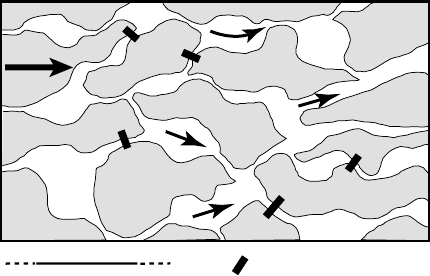
Types of subglacial drainage system 229

5 m

Temporary blockages

Ice

flow

Figure 8.22. Possible

geometry of a linked-

water-pocket drainage system

on till at the base of an ice

sheet.

and that the ﬂuctuations in some holes were well correlated, while those

in others showed no correlation whatsoever. Indeed, holes that showed

good correlation over some time periods showed no correlation over

other time periods. Finally, while water levels in holes within ∼10

of one another were often, but not always comparable, levels in more

distant holes commonly differed by several meters. Pressures in some

holes even rose above the estimated overburden pressure on occasion.

A distributed drainage system consisting of wide shallow linked

water pockets (Figure 8.22) with links periodically blocked by deforma-

tion of till or ice, would be compatible with all of these observations.

Individual pockets might be meters across and millimeters to tens of

millimeters deep and links might be centimeters wide. In such a system,

one can readily imagine that some holes might bottom in areas between

pockets and have difﬁculty forcing a connection to one, that a pressure

wave initiated at one borehole might have to travel a long distance down

one tortuous waterway and then up another in order to reach a nearby

hole, that when a conduit became blocked the water pressure in it might

rise temporarily and be out of phase with pressure variations in other

holes, and even that pressures might rise above the overburden pressure

in waterways that were blocked downstream but remained connected

upstream. Also conducive to development of a distributed drainage sys-

tem is the fact that the water source, basal melting, is distributed.

In summary, there is good theoretical and observational evidence

supporting the conclusion that conduits on till beneath ice sheets are

probably wide and shallow and that they form a distributed drainage

network. Beneath steeper valley glaciers, conduits may be narrower and

deeper, and may form an arborescent drainage system. Consistent with a

distributed drainage system on till beneath ice sheets is the observation

that landforms characteristic of dendritic drainage networks, such as

eskers (see below), are much less common in areas where the ice sheet

230 Water ﬂow in and under glaciers

moved over a thick till unit (Clark and Walder, 1994). Instead, gravel

lenses, some of which are known to be ribbon-like, elongated in the

direction of ice ﬂow, are common in till deposited by continental ice

sheets. These are interpreted to be the beds of wide shallow subglacial

conduits (Eyles et al., 1982; Brown et al., 1987).

Temporal and spatial distribution of drainage system types

Although we have been treating drainage systems on hard beds and

soft beds separately, most glaciers rest on bedrock in some areas and

on loose material in others. The character of the loose material is also

quite variable. Till beneath valley glaciers commonly contains substantial

amounts of sand and gravel, while that beneath Antarctic ice streams and

that overridden by the Laurentide Ice Sheet in the midwestern United

States is much ﬁner. This is probably largely a consequence of the nature

of the bedrock supplying the debris: resistant mountain ranges on the

one hand and large areas of weak sedimentary rock on the other. The

granulometry of the till affects the angle of internal friction and thus its

strength (Chapter 7). Also affecting till strength is the effective pressure,

which is typically higher beneath valley glaciers and lower beneath ice

sheets. These two factors combined make till deformation more likely

beneath ice sheets. From the point of view of a valley glacier, coarse

till that is not deforming may look very much like rough bedrock and

the drainage system developed on it may thus have characteristics of a

system on a hard bed.

Thus, the nature of the drainage system must vary from place to

place beneath a glacier and from one glacier to another. Where basal

melting occurs, the melting is distributed, so some parts of any subglacial

drainage system must be distributed. Some systems may be entirely

distributed, while others may have an arborescent component. On short

time scales, both types of system are likely to be altered or disrupted by

ﬂow of the ice, though the linked cavity system, stabilized by the location

of cavities on the lee sides of bedrock obstacles, is less subject to such

change. On longer time scales, the drainage system at a particular place

must vary as the glacier proﬁle changes, the bed is eroded, and subglacial

materials are rearranged. The challenge, therefore, is to determine not

what type of conduit system is present beneath a particular glacier, but

rather the spatial distribution of the different types of system.

Surges

A surge is a rapid advance of a glacier, lasting from a few months to a

couple of years, that is unrelated to changes in mass balance. During a