Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel
Подождите немного. Документ загружается.


31
Дуги
Контуры
9-10 10-9 1-2 2-3 3-9 9-8 8-1 8-2 1-3
К
1
( 9-10-9 ) 1 1 0 0 0 0 0 0 0
К
2
(1-2-3-9-8-1) 0 0 1 1 1 1 1 0 0
К
3
(2-3-9-8-2) 0 0 0 1 1 1 0 1 0
К
4
(1-3-9-8-1) 0 0 0 0 1 1 1 0 1
F 1 1 1 2 3 3 2 1 1
P 1 2 8 2 6 5 1 5 2
При отыскании оптимального множества разрываемых дуг нужно учитывать
следующие правила:
1. Количество мест разрывов должно быть выбрано так, чтобы были разорваны
все контуры комплекса.
2. Если параметричность всех дуг одинакова, задача сводится к определению
минимального числа дуг, разрыв которых превращает комплекс в разомкнутую
подсистему. В этом случае следует найти дугу, имеющую максимальную
контурную степень. В данном примере максимальное значение f имеет дуга 3-9
или 9-8. Разрыв любой из этих дуг приведет к уменьшению числа контуров в
комплексе (у нас контуры К
2
, К
З
и К
4
окажутся разомкнутыми).
Из матрицы контуров вычеркивают эти контуры и вновь пересчитывают контурные
степени оставшихся дуг. Вновь разыскивают среди этих дуг дугу, имеющую
максимальную контурную степень, и исключают соответствующие контуры. Этот
процесс продолжают до тех пор, пока не останется контуров.
В настоящем примере все контуры могут быть разомкнуты после разрыва двух дуг
3-9 и 9-10 или 9-8 и 10-9, что свидетельствует о том, что решение задачи может
быть не единственным.
3. В общем случае, когда параметричность дуг комплекса различна, разрываемые
дуги выбираются так, чтобы их суммарная параметричность была минимальной.
Для определения наиболее выгодных мест разрыва в этом случае необходимо
найти всевозможные варианты разрываемых дуг (с учетом правила 1),
определить суммарные параметричности различных вариантов и найти среди
этих параметричностей минимальную. Множество разрываемых дуг с
минимальной суммарной параметричностью и будет оптимальным.
Для рассматриваемого примера в таблице 2.6 представлены различные варианты
множеств разрываемых дуг. Как видно из таблицы, минимальную суммарную
параметричность имеет множество дуг (2-3, 8-1, 9-10). Именно эти дуги следует
разрывать для превращения комплекса в разомкнутую ХТС в данном примере.
Таблица 2.6 – Варианты множеств разрываемых дуг комплекса (1, 2, 3, 8, 9, 10)
№ варианта
Множество разрываемых дуг
Суммарная
параметричность
1 1-2, 2-3, 9-10, 1-3 8 + 2 + 1 + 2 = 13
2 2-3, 9-10, 3-9 2 + 1 + 6 = 9
3 3-9, 9-10 6 + 1 =7
4 2-3, 8-1, 9-10 2 + 1 + 1 = 4

32
5 2-3, 8-1, 10-9 2 + 1 + 2 = 5
6
…………. ………….
2.4.6 Определение окончательной последовательности расчета
После разрыва дуг, входящих в оптимальное множество разрываемых дуг,
каждый комплекс превращается в разомкнутую подсистему, а вся ХТС в целом - в
разомкнутую систему. Для каждого разомкнутого комплекса с помощью
алгоритмов определения вычислительной последовательности разомкнутых
систем легко определить порядок расчета входящих в него элементов. Так, для
комплекса (1, 2, 3, 8, 9, 10) вычислительная последовательность расчета имеет
вид (1, 3, 10, 9, 8, 2).
Для решения дополнительных уравнений на местах разрыва в программах
расчета ХТС используются так называемые фиктивные итерационные блоки.
Предполагается, что в этих блоках задаются начальные приближения значений
параметров разорванных потоков и сводятся к минимуму рассогласования
значений параметров разорванных потоков. Способ включения итерационного
блока (ИБ) в информационную схему расчета ХТС показан на рисунке 2.9.
Последовательность расчета комплекса (1, 2, 3, 8, 9, 10) такова: в ИБ1 (на
выходе) задаются начальные приближения для параметров разорванных потоков
2-3, 8-1, 9-10. После этого, по известным математическим описаниям элементов в
определенной последовательности вычисляются выходные параметры аппаратов
1, 3, 10, 9, 8, 2.
В результате расчета на входе ИБ получаются последующие приближения для
параметров соответствующих разорванных потоков. Если разность значений
параметров потоков на входе и выходе ИБ больше заданной точности, то
задается новое приближение и поиск решения продолжается. Таким образом,
последовательность расчета рассматриваемого комплекса имеет вид:
(ИБ1, 1, 3, 10, 9, 8, 2).
Последовательность расчета комплекса (5, 11) не нуждается в пояснении.
Полученные последовательности расчета отдельных комплексов подставляют в
предварительную последовательность и получают окончательную
последовательность расчета ХТС. В рассматриваемом примере окончательная
последовательность расчета ХТС (Рисунок 2.10) имеет вид:
[ 7, (ИБ1, 1, 3, 10, 9, 8, 2), 4, (ИБ2, 5, 11), 6]

33
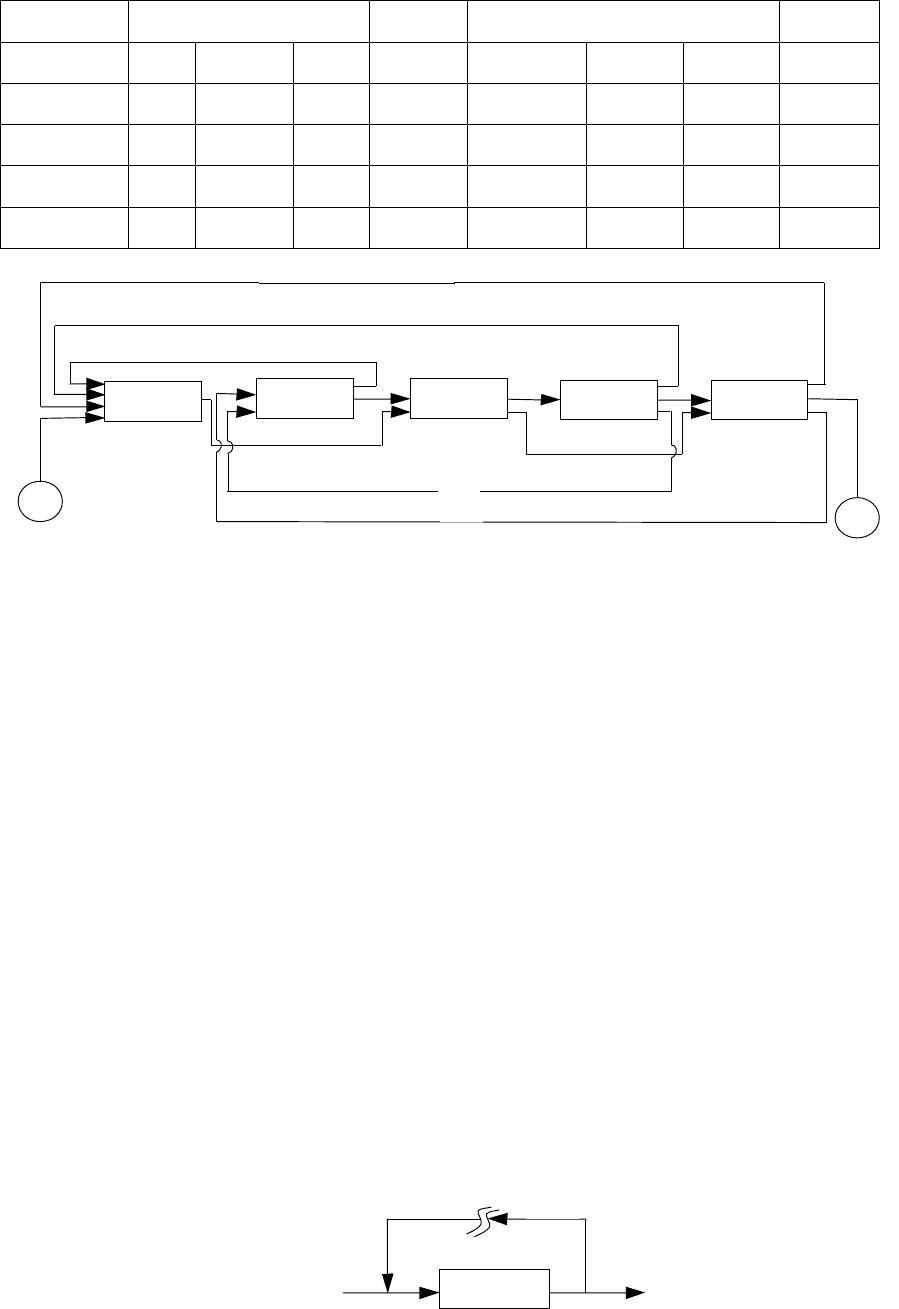
Рисунок 2.9 – Комплекс с дугами разной параметричности и соответствующая ему
разомкнутая ХТС
Рисунок 2.10 – Информационная блок-схема расчета комплекса 1:
на 1-ом (а) и 2-ом (б) этапах
Существует ещё один алгоритм определения оптимального множества
разрываемых дуг. Для этого структуру ХТС, изображенную на рисунке 2.11
представляют в следующем виде (Таблица 2.7).
1
2
3
8
9
10
1
2
3
8
9
10
а)
б)
1
2
3
8
9
10
1
2
3
8
9
10
34
S
3
S
1
S
8
S
5
S
2
S
9
S
10
PA
SA
P
1
P
2
P
5
P
4
P
3
PB
SB
S
6
S
7
S
4
X
Комплекс
Y(X)
Таблица 2.7 – Структура ХТС
Вершины
Входные потоки П Выходные потоки П
P
1
S
1
(3)
S
3
(1) S
4
(4)
8 S
2
(2) 2
P
2
S
6
(3)
S
7
(5) 8 S
1
(3) S
5
(1) 4
P
3
S
2
(2)
S
5
(1) 3 S
8
(7) S
9
(2) 9
P
4
S
8
(7)
7 S
3
(1) S
6
(3) S
10
(2) 6
P
5
S
9
(2)
S
10
(2) 4 S
4
(4) S
7
(5) 9
Рисунок 2.11 – Блок-схема ХТС
В таблице 2.7 в скобках указана параметричность каждого потока. П – суммарная
параметричность входных или выходных потоков.
Алгоритм состоит из следующих шагов:
1. Отыскивается вершина с минимальной суммарной параметричностью входных
потоков. Из этих вершин определяется вершина с максимальной суммарной
параметричностью выходных потоков.
2. Разрываются входные потоки, соответствующие данной вершине.
3. Проверяется, все ли контуры разорваны.
4. Если да, то алгоритм закончен, если нет, то алгоритм продолжается с первого
шага.
Для рассматриваемого примера разрыв потоков S2, S5 превращает замкнутую
ХТС в разомкнутую.
2.5 Итерационные методы для решения уравнений на местах разрывов
Для решения уравнений на местах разрыва могут быть использованы
традиционные методы решения систем нелинейных алгебраических уравнений.
Однако при этом должна быть учтена специфика декомпозиционного расчёта.
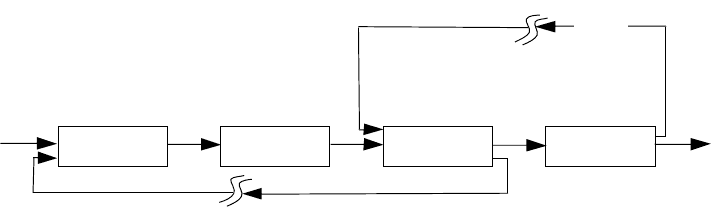
Как известно, в результате структурного анализа комплекс превращается в
разомкнутую систему (Рисунок 2.12). На месте разрыва необходимо решать
систему уравнений в неявном виде: X=Y(X)
Рисунок 2.12 – Представление комплекса после разрыва потоков
35
X
Y
u
P
4
v
P
3
P
2
P
1
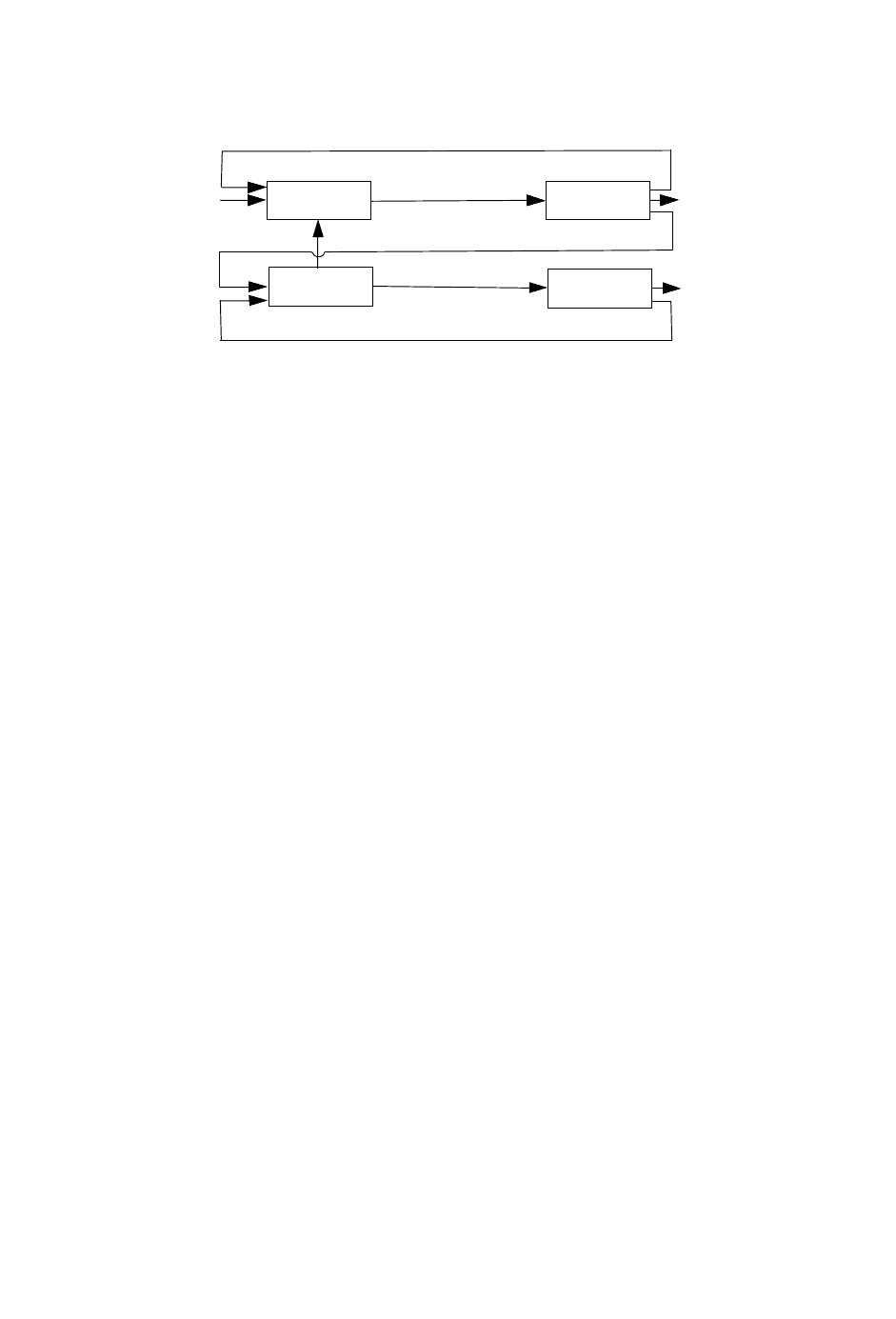
Рисунок 2.13 – Представление комплекса после множественного разрыва потоков
В случае множественного разрыва потоков (Рисунок 2.13) на местах разрыва
необходимо решать уравнения: U = V(U, X), Y = X(U, X).
Для решения этих уравнений в современных программных продуктах
используются следующие методы:
– метод простой итерации,
– метод Вегстейна,
– метод Ньютона-Рафсона и другие.
В общем случае на местах разрыва необходимо решать следующую систему из n
нелинейных алгебраических уравнений с n неизвестными:
f
i
(x
1
, x
2
,…, x
n
)=0, i=1,2,…,n.
2.5.1 Метод простой итерации
Для применения метода простой итерации система рассматриваемых уравнений
преобразуется к следующему виду:
x
i
=f
i
(x
1
, x
2
,…, x
n
), i=1,2,…,n.
Задаются начальные приближения и осуществляется поиск решения по этому
преобразованному уравнению.
Необходимо отметить, что на сходимость процедуры поиска решения сильно
влияет способ представления преобразованных уравнений и выбор начального
приближения.
Пример 1
Рассмотрим решение уравнения
x
3
-x-1=0 (2.1)
Начальное приближение x
(0)
=0, точность решения
=10
-2
Представим уравнение в виде: x=x
3
-1 (2.2)
Результаты, приведенные в таблице 2.8 показывают, что процесс решения
расходится.

36
Таблица 2.8 – Результаты решения уравнения (2.2) методом простой итерации
k x
k
x
(k+1)
0 0 -1
1 -1 -2
2 -2 -9
3 -9 -730
4 -730
5.3
10
-8
Представим уравнение (2.1) в виде:
3
1xx (2.3)
Результаты, приведенные в таблице 2.9, показывают, что процесс решения
сходится.
Таблица 2.9 – Результаты решения уравнения методом простой итерации
k
x
( )k
x
)( 1k
0 0 1
1 1 1.26
2 1.26 1.32
3 1.32 1.325
4 1.325 1.326
При
)(
)()( 54
xx
выполняется условие сходимости 010xx
54
,
)()(
и
итерационный процесс заканчивается.
Пример 2
Рассмотрим решение системы уравнений:
198xxxbx
111xxxxa
2
2
3
121
3
2
2
121
(2.4)
Начальное приближение
),(
)(
11x
0
, при a = 100, b = 100.
Представим систему в виде:
),(,,,,
),(,,,,
212
2
2
3
112
211
3
2
2
121
xx981x010x010x010x
xx111x010x010x010x
(2.5)
В таблице 2.10 показан ход итерационного процесса поиска решения системы
(2.5).

37
Таблица 2.10 – Ход итерационного процесса
k
)(k
1
x
)( 1k
2
x
0 1 1
1 1.08 1.97
2 1.00218 1.99541
3 1.00055 1.99973
4 1.00002 1.99997
5 1.00000 2.00000
2.5.2 Метод Вегстейна
В соответствии с этим методом каждое последующее приближение x
k+1
определяется через предыдущее x
k
по формуле:
)(
)()()()( 1k
i
k
ii
k
i
1k
i
xxtxx
, (2.6)
где t – скалярная величина,
)()()(
)()(
2k
i
k
i
1k
i
1k
i
k
i
i
xxx2
xx
t
Ход итерационного процесса при решении примера 2 методом Вегстейна
представлен в таблице 2.11.
Таблица 2.11 – Ход итерационного процесса при решении методом Вегстейна
k x
1
x
2
t
1
t
2
0 1 1 -0.493 0.027
1 1.08 1.97 -0.33 0.028
2 1.002 1.995 -0.248 0.028
3 1.041 1.996 -0.199 0.029
4 1.028 1.996
5 1.031 1.996
6 1.03 1.996
7 1.03 1.996
38
3 Пример декомпозиционного расчета ХТС с использованием
метода простой итерации
3.1 Постановка задачи
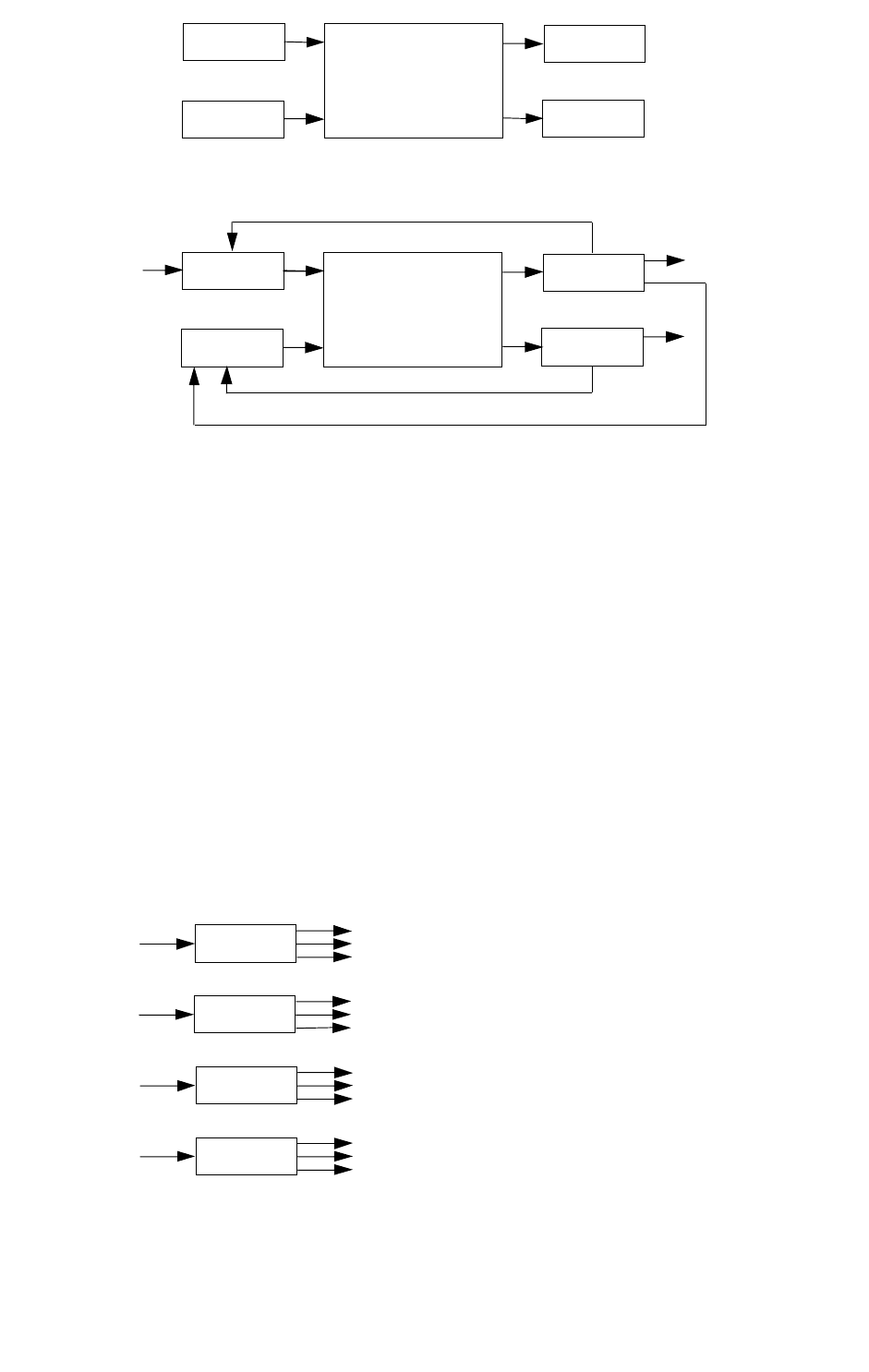
Определить расходы промежуточных и выходных потоков ХТС (Рисунок 3.1).
Пусть ;чкг 1000G
-1
01
;G1,0G
1221
;GG2,0G
432331
;G3,0G
1223
.G4,0G
3443
Рисунок 3.1 – Химико-технологическая система
Здесь и в дальнейшем приняты следующие обозначения:
ij
G – расход потока,
выходящего из i-го элемента и поступающего в j-й элемент. Если первый индекс – 0,
то поток соответствует входному потоку ХТС, если второй индекс – 0, поток
соответствует выходному потоку ХТС.
3.2 Структурный анализ ХТС
Все элементы ХТС образуют комплекс, т. е. могут быть рассчитаны только
совместно. С помощью прадерева можно выделить следующие контуры:
343K ,1321K ,121K
321
Так как параметричность всех потоков одинакова (каждый поток характеризуется
только расходом), то для преобразования замкнутой ХТС в разомкнутую можно
воспользоваться, например, разрывом дуг 1-2 и 3-4.
Окончательная последовательность расчета ХТС: (ИБ, 2, 4, 3, 1).
Информационная блок-схема расчета ХТС представлена на рисунке 3.2.
1
3
4
2
0,1
0,3
0,4
0,2
1000
39
Рисунок 3.2 – Этапы составления информационной блок-схемы
и определение последовательности расчета элементов ХТС
3.3 Составление математических описаний элементов ХТС
Для расчета ХТС необходимо наличие математических описаний отдельных
элементов ХТС. В рассматриваемом примере их можно составить с помощью
соотношений между расходами потоков, заданных в условии.
Запишем математические описания элементов ХТС согласно определенной
ранее вычислительной последовательности (рисунок 3.3).
На рисунке 3.3
(p)
34
)p(
12
G ,G – расходы соответствующих потоков.
Таким образом, математическое описание данной ХТС представляет собой
систему из 8-и уравнений с 8-ю неизвестными.
Для решения данной задачи можно воспользоваться различными методами, в
данном случае
–
методом простой
итерации. Этот метод носит общий характер и
с успехом применяется для расчета сложных реальных ХТС.
Рисунок 3.3 – Последовательность расчета элементов ХТС
1
ИБ
3
2
4
1
ИБ
3
2
4
2
4
3
1
G
21
=0,1
.
G
12
G
23
=0,3
.
G
12
G
20
=0,6
.
G
12
G
43
=0,4
.
G
34
G
40
=0,6
.
G
34
G
31
=0,2
.
(G
23
+G
43
)
)GG(8,0G
4323
)p(
34
312101
)p(
12
GGGG

40
Алгоритм решения задачи
Шаг 1.
Ввод исходных данных. В данном случае таковыми будут:
01
G
–
расход
входного потока, кг·ч
-1
;
–
точность вычисления, %;
3412
G ,G
–
начальные
приближения для расходов на выходе ИБ.
Шаг 2.
Задание номера итерации,
k
=1.
Шаг 3.
Расчет ХТС в соответствии с найденной в результате структурного
анализа последовательностью, т. е. сначала необходимо для элемента 2
определить значения расходов для выходных потоков
202321
Gи G ,G
, затем — для
элемента 4:
,
4043
GG
, далее для элемента 3:
31
G и
)p(
34
G
и, наконец, для элемента
1 значение
G
)p(
12
.
Шаг 4.
Проверка условий
100
G
G-G
12
12
)p(
12
и
100
G
G-G
34
34
)p(
34
Шаг 5. Если эти условия выполнены, т. е. значения соответствующих расходов на
местах разрывов определены с большей погрешностью, чем
, то в соответствии
с методом простой итерации 1kk ,GG ,GG
)p(
3434
)p(
1212
и вычисления ХТС
повторяются, начиная с шага 3.
Шаг 6.
Если же условия не выполнены, т. е. значения соответствующих расходов
на местах разрыва найдены с заданной точностью, то выполняется шаг 7.
Шаг 7.
Печать числа итераций k, необходимых для расчета ХТС, и значений
расходов промежуточных и выходных потоков.
По приведенному выше алгоритму была составлена программа для реализации
задачи с помощью электронной таблицы Excel и системы компьютерной
математики Mathcad.
3.4 Решение задачи с помощью электронной таблицы Excel и системы
компьютерной математики Mathcad
3.4.1 Решение задачи с помощью электронной таблицы Excel
Подготовка задачи для решения в рамках Excel проводится в следующей
последовательности:
1. Выбор ячеек для поисковых переменных,
2. Задание в них координат исходной точки поиска,
3. Выбор ячейки для значения целевой функции,
4. Запись в ней формулы для её вычисления,
5. Выбор ячеек для ограничений в виде функциональных неравенств,
6. Запись в ячейках формул для их вычисления,
7. выбор ячеек для ограничений в виде функциональных равенств,
8. записи в ячейках формул для их вычисления.
