Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel
Подождите немного. Документ загружается.

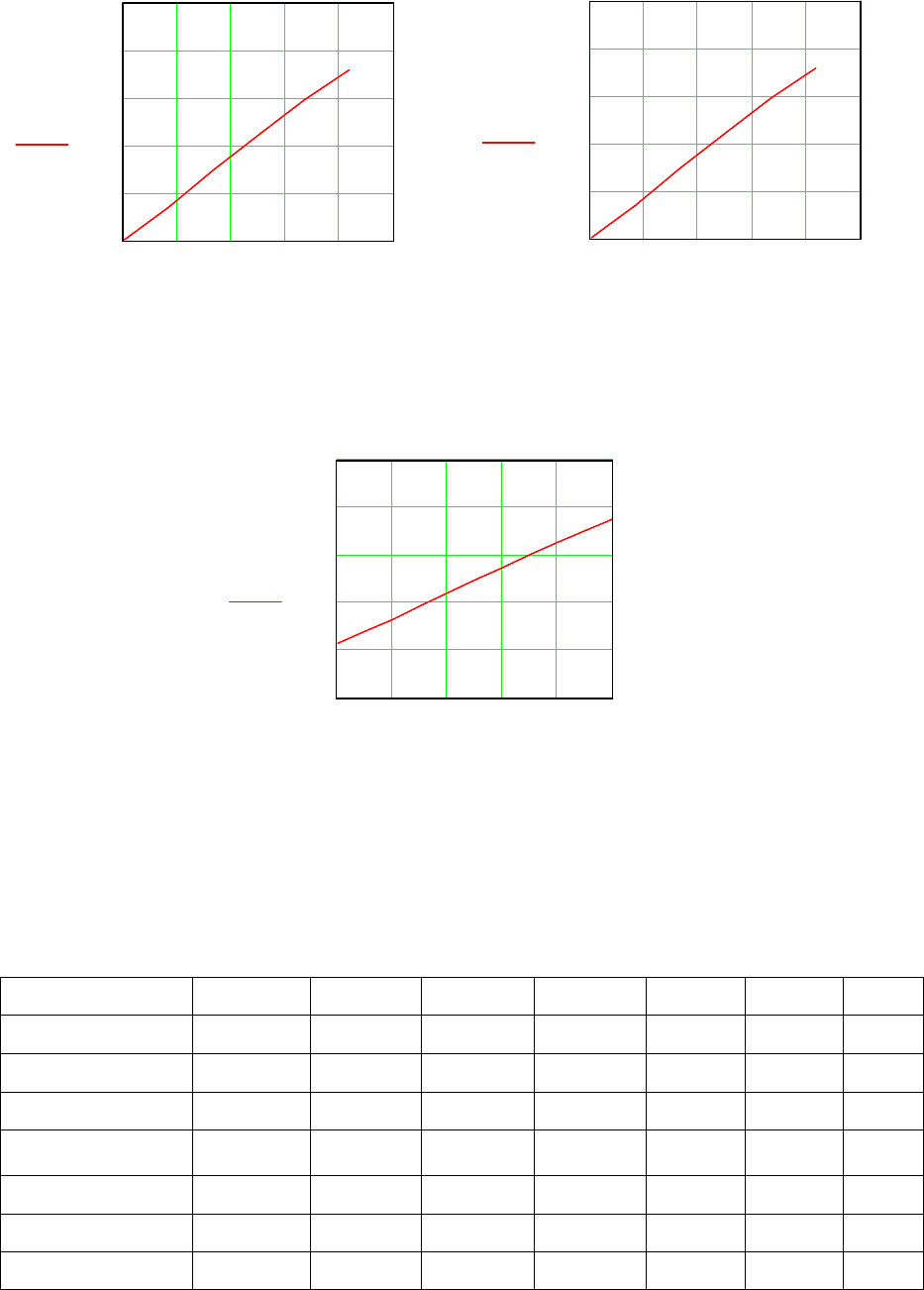
311
Рисунок 13.5 – Графики функции желательности
На основе этих частных функций желательности для всех композиций (Таблица
13.17) были получены следующие данные.
Таблица 13.17 – Результаты вычислений
Номер опыта
y
1
y
2
y
3
d
1
d
2
d
3
D
1 3572 1139 344.7 0.349 0.659 0.914 0.594
2 3840 1189 312.9 0.46 0.692 0.877 0.653
3 3618 993.1 603.7 0.368 0.548 0.996 0.586
4 4914 1398 373 0.79 0.8 0.94 0.84
5 3467 1208 316 0.305 0.704 0.881 0.574
6 3233 1119 569.6 0.213 0.645 0.994 0.515
7 4092 961 468 0.558 0.522 0.98 0.658
600 720 840 960 1080 1200
0.2
0.32
0.44
0.56
0.68
0.8
y x( )
x
600 720 840 960 1080 1200
0.2
0.32
0.44
0.56
0.68
0.8
y x( )
x
x 3200 3300 4300
x 600 700 1100
a 4.106
b 0.001135
a
1.973
b 0.002496
y x( ) exp exp a b x( )( )
y x( ) exp exp a b x( )( )
x 100 110 200
b
0.012
a
1.724
y x( ) exp exp a b x( )( )
100 120 140 160 180 200
0
0.16
0.32
0.48
0.64
0.8
y x( )
x

312
Номер опыта
y
1
y
2
y
3
d
1
d
2
d
3
D
8 3621 1251 405.5 0.369 0.73 0.958 0.637
9 3527 1266 474.1 0.33 0.738 0.981 0.621
10 4708 1082 159.5 0.748 0.618 0.437 0.587
11 4755 1028 134.2 0.76 0.577 0.326 0.523
12 4461 654.5 95.39 0.681 0.247 0.168 0.304
13 4901 1077 237 0.79 0.61 0.72 0.71
14 5187 964.7 71.13 0.845 0.525 0.092 0.344
15 3292 916.5 98.98 0.235 0.483 0.181 0.274
16 4955 1150 144.3 0.803 0.667 0.37 0.583
17 4944 1088 112 0.801 0.623 0.232 0.487
18 4585 1475 217 0.72 0.84 0.66 0.73
19 6095 1018 74.77 0.942 0.569 0.102 0.379
20 5944 1229 27.97 0.931 0.717 0.018 0.23
21 5694 958.4 162.7 0.91 0.519 0.451 0.597
22 5720 1081 24.84 0.912 0.618 0.016 0.206
23 5448 849.1 36.27 0.882 0.423 0.027 0.215
24 4568 1081 106.1 0.712 0.618 0.208 0.451
25 6216 1019 36.15 0.949 0.57 0.026 0.243
26 6015 1042 66.12 0.936 0.588 0.079 0.352
27 5777 1177 225 0.92 0.68 0.69 0.76
Как видно из таблицы, наибольшее значение обобщенной функции
желательности получено в четвертом опыте (D = 0,84). Хорошие
композиции получены также в опытах 13, 18 и 27.
13.4.3 Решение многокритериальной задачи по обобщенному критерию с
помощью Excel
Задачу оптимизации сформулируем следующим образом:
Найти минимум
)xxx,x(D
4,3,21
по поисковым переменным
43,21
x,xx,x при наличии ограничений
– на поисковые переменные:
iii
xsupxxinf , I = 1(1)4;
– на частные функции желательности
3,21
yy,y :
jjj
ysupyyinf , j=1(1)3.
В таблице 13.18 приведены результаты решения задачи, полученные с помощью
электронной таблицы Excel.
313
Таблица 13.18 – Результаты решения задачи
Значения факторов
x
1
x
2
x
3
x
4
y
1
y
2
y
3
1536.803 1320.922 807 777 6 150 1 430 493
мин
932 992 807 247 3 240 660 25
макс
5279 5382 5877 1425 6 150 1430 493
d
1
d
2
d
3
0.945 0.818 1
D 0.918
Коэффициенты аппроксимации
-0.029 -1.00203 6273.4
-33.0429 49.25318 -2.192856
8.464873 -60.6792 -1.578662
0.996311 0.105961 -0.01593
60.73457 25.84323 -4.41996
-0.0038 -0.0436 1.72E-04
7.27E-04 -7.54E-03
3.34E-05
-0.01819 0.006029 2.02E-03
-2.20E-04 -0.00668 -2.52E-05
0.004017 -0.03033 -2.69E-04
-0.00159 -0.00133 -9.61E-05
0.008727 4.85E-06 2.17E-05
0.000472 0.062013 3.22E-04
2.72E-05 0.00778 3.46E-05
0.003204 0.003618 7.83E-05
Ниже представлены протоколы решения этой задачи в системе компьютерной
математики Mathcad.
x1 1540
x2 1330
x3 810
x4 780
b0
0.029
b1
33.043
b2 8.465
b3 0.996
b4
60.73
b5 0.0038
b6 7.27 10
4
b7
0.0182
b8 2.2 10
4
b9
0.004
b10 0.0016
b11
0.0087
b12
0.000472
b13 2.72 10
5
b14
0.0032
Вычисление d1
e1 x1 x2 x3 x4( ) b0 b1 x1 b2 x2 b3 x3 b4 x4

314
e3 x2 x3 x4( ) b8 x2 x3 b9 x2
x4
e4 x3 x4( ) b10 x3
x4
e5 x1 x2 x3 x4( ) b11 x1
2
b12 x2
2
b13 x3
2
b14 x4
2
g11 x1 x2 x3 x4( ) e1 x1 x2 x3 x4( ) e2 x1 x2 x3 x4( )
g12 x1 x2 x3 x4( ) g11 x1 x2 x3 x4( ) e3 x2 x3 x4( )
y1 x1 x2 x3 x4( ) g12 x1 x2 x3 x4( ) e4 x3 x4( ) e5 x1 x2 x3 x4( )
y1 x1 x2 x3 x4( ) 6.145 10
3
d1r x1 x2 x3 x4( ) 0.945
Вычисление d2
c0
1.00203
c1
49.253
c2
60.67916
c3
0.10596
c4
25.843
c5
0.0436
c6
0.00754
c7
0.006
e2 x1 x2 x3 x4( ) b5 x1 x2 b6 x1 x3 b7 x1 x4
d1r x1 x2 x3 x4( ) exp exp 4.106 0.001135 y1 x1 x2 x3 x4( )( )[ ][
]
c8 0.00668
c9
0.0303
c10
0.00133
c11 4.85 10
6
c12
0.06201
c13
0.00778
c14
0.00362
k1 x1 x2 x3 x4( ) c0 c1 x1 c2 x2 c3 x3 c4 x4
k2 x1 x2 x3 x4( ) c5 x1 x2 c6 x1 x3 c7 x1 x4
k3 x1 x2 x3 x4( ) c8 x2 x3 c9 x2 x4
k4 x3 x4( ) c10 x3 x4
k5 x1 x2 x3 x4( ) c11 x1
2
c12 x2
2
c13 x3
2
c14 x4
2
k11 x1 x2 x3 x4( ) k1 x1 x2 x3 x4( ) k2 x1 x2 x3 x4( )
k12 x1 x2 x3 x4( ) k11 x1 x2 x3 x4( ) k3 x1 x2 x3 x4( )
y2 x1 x2 x3 x4( ) k12 x1 x2 x3 x4( ) k4 x3 x4( ) k5 x1 x2 x3 x4( )
d2r x1 x2 x3 x4( ) exp exp 1.973 0.0025 y2 x1 x2 x3 x4( )( )[ ][
]
y2 x1 x2 x3 x4( ) 1.427 10
3
d2r x1 x2 x3 x4( ) 0.816
Вычисление d3
d0
6273.4
d1
2.193
d2
1.58
d3 0.016
d4
4.42
d5 1.72 10
4
d6 3.34 10
5
d7 2.02 10
3
d8 2.52 10
5
d9 2.69 10
4
d10 9.61 10
5
d11 2.17 10
5
d12 3.22 10
4
d13 3.46 10
5
d14 7.83 10
5
f1 x1 x2 x3 x4( ) d0 d1 x1 d2 x2 d3 x3 d4 x4
f2 x1 x2 x3 x4( ) d5 x1 x2 d6 x1 x3 d7 x1 x4
f3 x2 x3 x4( ) d8 x2 x3 d9 x2 x4
f4 x3 x4( ) d10 x3 x4
f5 x1 x2 x3 x4( ) d11 x1
2
d12 x2
2
d13 x3
2
d14 x4
2
h11 x1 x2 x3 x4( ) f1 x1 x2 x3 x4( ) f2 x1 x2 x3 x4( )
315
13.4.4 Использование функции желательности в нормированном виде
Рассмотрим использование другого вида функции желательности для решения этой
задачи:
)yy(
)yy(
d
мин,iмакс,i
мин,ii
i
.
В таблице 13.19 представлены расчетные значения рассматриваемой функции
желательности.
Таблица 13.19 – Расчетные значения функции желательности
Номер опыта
y
1
y
2
y
3
d
1
d
2
d
3
D
1 3572 1139 344.7 0.114 0.59 0.553 0.333
2 3840 1189 312.9 0.203 0.651 0.498 0.404
3 3618 993.1 603.7 0.129 0.413 1 0.376
4 4914 1398 373.1 0.564 0.905 0.602 0.675
5 3467 1208 316 0.078 0.674 0.503 0.298
h12 x1 x2 x3 x4( ) h11 x1 x2 x3 x4( ) f3 x2 x3 x4( )
y3 x1 x2 x3 x4( ) h12 x1 x2 x3 x4( ) f4 x3 x4( ) f5 x1 x2 x3 x4( )
d3r x1 x2 x3 x4( ) exp exp 1.724 0.012 y3 x1 x2 x3 x4( )( )[ ][
]
y3 x1 x2 x3 x4( ) 479.061
d3r x1 x2 x3 x4( ) 0.982
Решение задачи оптимизации
D x1 x2 x3 x4( )
3
d1r x1 x2 x3 x4( ) d2r x1 x2 x3 x4( ) d3r x1 x2 x3 x4( )
Given
x1
5279
x2
5382
x3
5877
x4 1425
x1
932
x2
992
x3
807
x4
247
y1 x1 x2 x3 x4( ) 3240
y1 x1 x2 x3 x4( ) 6150
y2 x1 x2 x3 x4( ) 660
y2 x1 x2 x3 x4( ) 1430
y3 x1 x2 x3 x4( ) 25
y3 x1 x2 x3 x4( )
493
x1
x2
x3
x4
Maximize D x1 x2 x3 x4( )
x1
x2
x3
x4
1.53 10
3
1.32 10
3
812.578
775.673
D x1 x2 x3 x4( ) 0.913

316
Номер опыта
y
1
y
2
y
3
d
1
d
2
d
3
D
6 3233 1119 569.6 0 0.566 0.941 0
7 4092 961 468 0.288 0.373 0.766 0.435
8 3621 1251 405.5 0.13 0.727 0.658 0.396
9 3527 1266 474.1 0.099 0.745 0.776 0.385
10 4708 1082 159.5 0.494 0.521 0.233 0.391
11 4755 1028 134.2 0.51 0.455 0.189 0.353
12 4461 654.5 95.39 0.412 0 0.122 0
13 4901 1077 236.5 0.559 0.514 0.366 0.472
14 5187 964.7 71.13 0.655 0.378 0.08 0.271
15 3292 916.5 98.98 0.02 0.319 0.128 0.093
16 4955 1150 144.3 0.577 0.604 0.206 0.416
17 4944 1088 112 0.574 0.529 0.15 0.357
18 4585 1475 216.8 0.453 1 0.332 0.532
19 6095 1018 74.77 0.959 0.443 0.086 0.332
20 5944 1229 27.97 0.909 0.7 0.005 0.151
21 5694 958.4 162.7 0.825 0.37 0.238 0.418
22 5720 1081 24.84 0.834 0.52 0 0
23 5448 849.1 36.27 0.743 0.237 0.02 0.151
24 4568 1081 106.1 0.448 0.52 0.14 0.32
25 6216 1019 36.15 1 0.445 0.02 0.206
26 6015 1042 66.12 0.933 0.472 0.071 0.315
27 5777 1177 225.4 0.853 0.636 0.346 0.573
Минимальные
значения y
i
3233 655 25
Максимальные
значения y
i
6216 1 475 604
В этом случае наибольшее значение обобщенной функции желательности
получено в четвертом опыте (D = 0.84). Хорошие композиции получены
также в опытах 18 и 27.
13.4.5 Решение задачи на основе маргинальных значений
Ниже представлен протокол решения рассматриваемой задачи на основе
маргинальных значений.
x1 1540
x2 1330
x3 810
x4 780
b3 0.996
b0
0.029
b4
60.73
b1
33.043
b2 8.465
b5 0.0038
b6 7.27 10
4
b7
0.0182

317
b8 2.2 10
4
b9
0.004
b10
0.0016
b11
0.0087
b12
0.000472
Вычисление d1
e1 x1 x2 x3 x4( ) b0 b1 x1 b2 x2 b3 x3 b4
x4
e2 x1 x2 x3 x4( ) b5 x1 x2 b6 x1 x3 b7 x1
x4
e3 x2 x3 x4( ) b8 x2 x3 b9 x2
x4
e4 x3 x4( ) b10 x3
x4
e5 x1 x2 x3 x4( ) b11 x1
2
b12 x2
2
b13 x3
2
b14 x4
2
g11 x1 x2 x3 x4( ) e1 x1 x2 x3 x4( ) e2 x1 x2 x3 x4( )
b13 2.72 10
5
b14
0.0032
g12 x1 x2 x3 x4( ) g11 x1 x2 x3 x4( ) e3 x2 x3 x4( )
y1 x1 x2 x3 x4( ) g12 x1 x2 x3 x4( ) e4 x3 x4( ) e5 x1 x2 x3 x4( )
y1 x1 x2 x3 x4( ) 6.145 10
3
Вычисление d2
c0
1.00203
c1
49.253
c2 60.67916
c3
0.10596
c4
25.843
c5 0.0436
c6
0.00754
c7 0.006
c8 0.00668
c9
0.0303
c10
0.00133
c11 4.85 10
6
c12
0.06201
c13
0.00778
c14
0.00362
k1 x1 x2 x3 x4( ) c0 c1 x1 c2 x2 c3 x3 c4 x4
k2 x1 x2 x3 x4( ) c5 x1 x2 c6 x1 x3 c7 x1 x4
k3 x1 x2 x3 x4( ) c8 x2 x3 c9 x2 x4
k4 x3 x4( ) c10 x3 x4
k5 x1 x2 x3 x4( ) c11 x1
2
c12 x2
2
c13 x3
2
c14 x4
2
k11 x1 x2 x3 x4( ) k1 x1 x2 x3 x4( ) k2 x1 x2 x3 x4( )
k12 x1 x2 x3 x4( ) k11 x1 x2 x3 x4( ) k3 x1 x2 x3 x4( )
y2 x1 x2 x3 x4( ) k12 x1 x2 x3 x4( ) k4 x3 x4( ) k5 x1 x2 x3 x4( )
y2 x1 x2 x3 x4( ) 1.427 10
3
Вычисление d3
d0
6273.4
d1
2.193
d2
1.58
d3 0.016
d4
4.42
d5 1.72 10
4
d6 3.34 10
5
d7 2.02 10
3
d8 2.52 10
5
d12 3.22 10
4
d13 3.46 10
5
d14 7.83 10
5
f1 x1 x2 x3 x4( ) d0 d1 x1 d2 x2 d3 x3 d4 x4
f2 x1 x2 x3 x4( ) d5 x1 x2 d6 x1 x3 d7 x1 x4
d9 2.69 10
4
d10 9.61 10
5

318
13.4.6 Решение задачи на основе нечетких множеств
Воспользуемся в качестве функций принадлежности частных критериев множеству
наилучших решений частными функциями желательности.
В таблице 13.20 приведены рассчитанные значения функций принадлежности.
Таблица 13.20 – Значения функций принадлежности
Функции
принадлежности
Номер
опыта
d
1
d
2
d
3
Минимальное
значение
функции
принадлежности
Максимальное
значение
функции
принадлежности
1 0.349 0.659 0.914 0.349 0.914
d11 2.17 10
5
f3 x2 x3 x4( ) d8 x2 x3 d9 x2 x4
f4 x3 x4( ) d10 x3 x4
f5 x1 x2 x3 x4( ) d11 x1
2
d12 x2
2
d13 x3
2
d14 x4
2
h11 x1 x2 x3 x4( ) f1 x1 x2 x3 x4( ) f2 x1 x2 x3 x4( )
h12 x1 x2 x3 x4( ) h11 x1 x2 x3 x4( ) f3 x2 x3 x4( )
y3 x1 x2 x3 x4( ) h12 x1 x2 x3 x4( ) f4 x3 x4( ) f5 x1 x2 x3 x4( )
y3 x1 x2 x3 x4( ) 479.061
Решение задачи оптимизации на основе маргинальных значений
D1 x1 x2 x3 x4( ) 6150 y1 x1 x2 x3 x4( )( )
2
D2 x1 x2 x3 x4( ) 1430 y2 x1 x2 x3 x4( )( )
2
D3 x1 x2 x3 x4( ) 493 y3 x1 x2 x3 x4( )( )
2
D x1 x2 x3 x4( ) D1 x1 x2 x3 x4( ) D2 x1 x2 x3 x4( ) D3 x1 x2 x3 x4( )
Given
x1
5279
x2
5382
x3
5877
x4 1425
x1
932
x2
992
x3
807
x4
247
x1
x2
x3
x4
Minimize D x1 x2 x3 x4( )
x1
x2
x3
x4
1.53 10
3
1.319 10
3
810.888
776.226
D x1 x2 x3 x4( ) 4.017 10
8
319
Функции
принадлежности
2 0.46 0.692 0.877 0.46 0.877
3 0.368 0.548 0.996 0.368 0.996
4 0.79 0.8 0.94 0.79 0.94
5 0.305 0.704 0.881 0.305 0.881
6 0.213 0.645 0.994 0.213 0.994
7 0.558 0.522 0.98 0.522 0.98
8 0.369 0.73 0.958 0.369 0.958
9 0.33 0.738 0.981 0.33 0.981
10 0.748 0.618 0.437 0.437 0.748
11 0.76 0.577 0.326 0.326 0.76
12 0.681 0.247 0.168 0.168 0.681
13 0.79 0.61 0.72 0.61 0.79
14 0.845 0.525 0.092 0.092 0.845
15 0.235 0.483 0.181 0.181 0.483
16 0.803 0.667 0.37 0.37 0.803
17 0.801 0.623 0.232 0.232 0.801
18 0.72 0.84 0.66 0.66 0.84
19 0.942 0.569 0.102 0.102 0.942
20 0.931 0.717 0.018 0.018 0.931
21 0.91 0.519 0.451 0.451 0.91
22 0.912 0.618 0.016 0.016 0.912
23 0.882 0.423 0.027 0.027 0.882
24 0.712 0.618 0.208 0.208 0.712
25 0.949 0.57 0.026 0.026 0.949
26 0.936 0.588 0.079 0.079 0.936
27 0.92 0.68 0.69 0.68 0.92
Минимаксная стратегия – максимальное значение из минимальных функций
принадлежности приводит к наилучшему решению в опыте 4.
Максиминная стратегия – минимальное значение из максимальных функций
принадлежности приводит к наилучшему решению в опыте 24.
13.5 Использование множителей Лагранжа и схемы компромиссов для
решения задач многоцелевой оптимизации
Если функциональная зависимость обобщенного критерия от частных
критериев установлена, то для решения задачи оптимизации можно
использовать метод неопределенных множителей Лагранжа.
320
Рассмотрим следующую задачу векторной оптимизации:
)x(fminf
i
Xx
opti
, k,1i .
Метод
– ограничений предполагает видоизменение постановки этой задачи:
)x(fminf
1
Xx
opt1
,
с учетом ограничений на остальные критерии оптимальности:
)x(f
i
,k,2i;
i
где
i
– максимальные допустимые (пороговые) значения критериев оптимальности,
кроме первого.
Для решения задачи составляется функция Лагранжа
k
2i
iii1
)x(f)x(fL
,
где
i
– неопределенные множители Лагранжа.
Рассмотрим два примера использования этого метода.
Пример 1
В этой задаче используются два критерия оптимальности и две управляемые
независимые переменные
6)10x()6x()x,x(f
5)4x()2x()x,x(f
min
2
2
2
1212
2
2
2
1211
x,x
21
Решение
Первая фаза решения состоит в преобразовании исходной постановки задачи:
)x,x(fmin
211
x,x
21
с учетом ограничения
2212
)x,x(f
.
Построим функцию Лагранжа
].)x,x(f[)x,x(f),x,x(L
2212122111221
Подставляя в нее выражения для
1
f и
2
f получим
],6)10x()6x[(54x)2x(),x,x(L
2
2
2
2
112
2
2
2
11221
здесь
12
– неопределенный множитель Лагранжа.
Найдем частные производные от функции Лагранжа по всем
:
аргументам и
приравняем их к нулю:
.0]6)10x()6x[(
L
;0)10x(2)4x(2
x
L
;0)6x(2)2x(2
x
L
2
2
2
2
1
12
2122
2
1121
1
Решив систему, получим соотношение:
.
x10
4x
x6
2x
2
2
1
1
12
Условие 0
12
гарантирует неулучшаемое решение. Тогда верхние и нижние
пределы для
1
x и
2
x имеют вид .10x4;6x2
21
