Хлопков Ю.И., Жаров В.А., Горелов С.Л. Лекции по теоретическим методам исследования турбулентности

Подождите немного. Документ загружается.

Рис. 8. Диаграммы, соответствующие членам ряда

теории возмущений (188) для поля скорости

Хотя мы не отмечаем на диаграммах волновые числа, но следует заметить, что три

элемента всегда встречаются в вершине, в которой всегда выполняются законы сохранения.

Поэтому мы считаем, что волновое число слева от вершины равно сумме волновых чисел двух

элементов справа.

Наш следующий шаг нацелен на то, чтобы из этих элементов получить диаграммное

разложение для точной корреляции. Другими словами, нам хотелось бы иметь диаграммное

разложение для точной корреляции

Q, выраженное через элементы Q

(0)

, G

(0)

и вершину M. Все, что

нам нужно – это графический эквивалент факторизации моментов четного порядка в виде

произведений парных корреляций.

На самом деле способ, которым мы это сделаем, очень прост. Расположим любые пары

диаграмм ветвями друг к другу, а затем соединим все полностью независимые сплошные линии

так, чтобы соединить две диаграммы всеми возможными способами и отметим, что две скорости

связаны с помощью крестика, который помещается в точке соединения. Численный множитель

получается умножением каждой диаграммы на число способов, с помощью которых соединение

линий дает одну и ту же диаграмму. Этот процесс проиллюстрирован на рис. 9, где мы показали

диаграммы нулевого порядка и два примера диаграмм второго порядка.

Таким способом можно написать полное разложение для точной парной корреляции до

любого порядка по параметру итераций. Следующий шаг состоит в поиске путей суммирования

этих членов во всех порядках. Следуя Уайлду, введем перенормированные диаграммные элементы

следующим образом:

жирная сплошная линия

↔u точная скорость

жирная пунктирная линия

↔G перенормированный

пропагатор

кружок ↔о перенормированная

вершина.

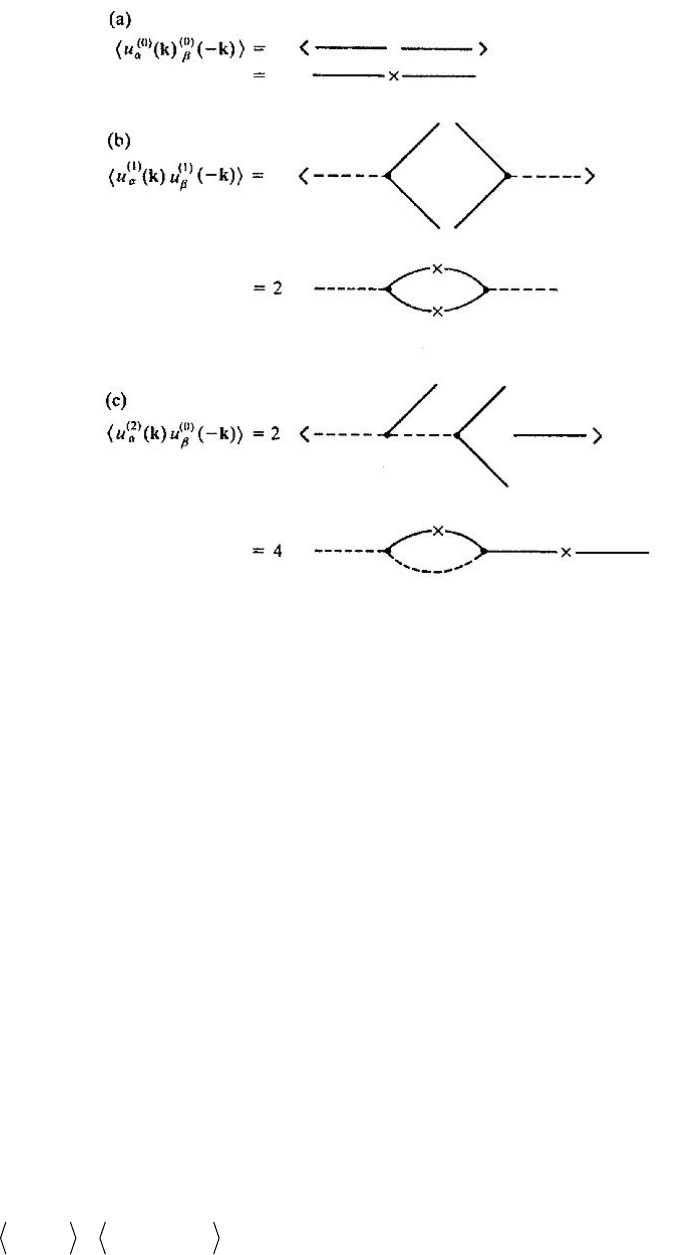
Рис. 9. Примеры процедуры осреднения с полем нулевого порядка,

приводящей к диаграммам разложении Q

αβ

(k; ω, ω′)

Отсюда следует, что в диаграммном обозначении точная парная корреляция – это две

жирных сплошных линии, соединенных крестиком.

Тем не менее подчеркнем, что мы не пользуемся этими элементами в данном изложении.

Мы вводим их только для того, чтобы объяснить основную идею. Будем снова следовать Уайлду,

и разделим проблему на две части. Снова привлекаемые идеи являются топологическими, и

основаны на классификации диаграмм на два типа: класс А и класс B. Поэтому с целью

напоминания временно сохраним полные обозначения и запишем точную парную корреляцию в

виде суммы отдельных вкладов от двух типов диаграмм, а именно:

бв бв бв

(;щ, щ)(;щ, щ)(;щ, щ)

QQ Q

′′

′

+kk k

, (195)

где

ω, ω′ – угловые частоты, связанные с помощью преобразования Фурье с временами t, t′. Теперь

мы рассмотрим по очереди два типа диаграмм.

Класс А диаграмм: перенормированный пропагатор

Класс А диаграмм определен как такие диаграммы, которые можно расщепить на две

части, разрезая одну независимую

(0)

линию. Если мы взглянем на первую (нулевого порядка)

диаграмму на рис. 9, то она как раз удовлетворяет определению диаграмм класса А. Ясно, что ее

можно интерпретировать с помощью уравнения (184) следующим образом:

(0) (0) (0) (0) (0) (0)

uu GfGf GGw==

, (196)

где последний шаг следует из (137), а

w – спектральная функция взбалтывающей силы.

Переходя ко второму порядку мы видим, что вторая диаграмма на рис. 9 не удовлетворяет

критерию для диаграмм класса А, а третья – удовлетворяет. И хотя мы не показываем это, каждый

легко может убедиться в том, что должно быть зеркальное отображение такой диаграммы, давая

две диаграммы класса А во втором порядке. Первая из них (которая показана) может иметь свою

(0)

линию слева, представленную в виде произведения G

(0)

w, в то время как вторая такая

диаграмма может иметь независимую Q

(0)

линию справа, факторизованную аналогичным образом.

Таким образом, во втором порядке имеется две группы диаграмм класса А, в которых спектр

взбалтывающей силы появляется вместе с

(0)

то с одной стороны, то с другой. Если мы будем

поступать таким образом с диаграммами класса А, то можем написать

бв

(;щ, щ)(,щ)(,щ)(;щ, щ)

QGGw

′′

′

kkkk

, (197)

где G(k, ω) – перенормированный пропагатор, равный сумме всех порядков соответствующим

образом модифицированных диаграмм класса А.

В этом месте следует заметить для дальнейшего, что подход Уайлда не является самым

общим. Фактически шаг, рассмотренный выше, эквивалентен утверждению, что точный

пропагатор определен системой откликов на взбалтывающую силу.

Класс В диаграмм: перенормированый ряд теории возмущений

В класс В диаграмм входят все те диаграммы, которые не попадают в класс А. Вернемся

опять к рис. 9. Первая из диаграмм второго порядка не может быть разделена на две части

разрывом одной

(0)

линии и поэтому является примером диаграмм класса В, которых во втором

порядке имеется только одна.

Теперь рассмотрим идеи, используемые при работе с диаграммами класса А. Мы уже

отмечали, что некоторые диаграммы соединены подобно

(0)

и, следовательно, являются

пропагатороподобными, поэтому просуммируем их все для получения перенормированного

пропагатора

G. Из чисто топологических соображений следует, что можно перенормировать

голую вершину, добавляя все диаграммы, соединенные подобно вершине.

Можно сформулировать общий алгоритм для этих процессов следующим образом:

1. 1. Выделим все диаграммы, которые не могут быть сведены к диаграммам низшего порядка

заменой частей этих диаграмм.

2. 2. Назовем иx неприводимыми диаграммами.

3. 3. Заменим все голые элементы в неприводимых диаграммах на их перенормированную

форму.

4. 4. Выпишем все эти модифицированные диаграммы по порядку, получив таким образом

перенормированный ряд теории возмущений.

Для полноты картины покажем результаты подобной процедуры, проведенной до

четвертого порядка на рис. 10, куда мы включили также диаграммы, полученные из диаграмм

класса А ранее.

Рис.10. Диаграммы, соответствующие интегральному уравнению для Q(k; ω, ω′)

В этом пункте рассмотрим те теории турбулентности, которые принадлежат к классу

перенормируемых теорий второго порядка и которые

не дают колмогоровский спектр в качестве

решения при больших числах Рейнольдса. Большую часть места отведем исторически важным

теориям, которые были призваны сыграть большую роль в рассматриваемой области

исследования. Мы обратимся к приближению прямых взаимодействий DIA Кречнана (1958), к

теории Эдвардса фоккер-планковского типа EFP (1964) и к теории самосогласованного поля

Геринга (1965).

Методика DIA была развита в ряде статей, закончившихся общей формулировкой в 1958

году. Ключевым моментом этой теории было введение функции бесконечно малого отклика .

Предположим, что взбалтывающая сила подвергнута флуктуации вида

f → f + δf, вводящей таким

образом соответствующую флуктуацию в поле скорости

u → u + δu, тогда для малых δf, δu

линеаризованный отклик системы можно записать как

ббв12

€

д (,) (,; , )д (, )

ut ddtG ttf t

−∞

′′

∫∫

kp kpp

′

, (198)

где – тензор бесконечно малого отклика.

бв

€

(,,,)Gtt

′

Уравнение для можно получить линеаризацией уравнений Навье–Стокса для малой

добавки. Очевидно, что будет флуктуировать от реализации к реализации, поэтому мы вводим

средний по ансамблю отклик в виде

€

GG=

, при этом, используя пространственную

однородность, результат можно записать в диагонализированной форме:

ббвв

€

д (,) (;, )д (, )

ut dtG ttft

−∞

′′

∫

′

. (199)

Здесь и далее мы следуем процедуре, описанной выше. Сначала делаем

λ-разложение,

затем заменяем каждое выражение нулевого порядка для

(0)

и G

(0)

на ренормализованные Q и G

соответственно, обрывая на втором порядке по

λ и полагая λ = 1. Для изотропного случая

результирующие уравнения для

Q и G имеют вид:

н (;, )

(,) (;,)

(;, ) (| |;,) д(

kGktt

ddsL Gjts

Gk st Q t s t t

∂

′

⎛⎞

′

⎜⎟

⎝⎠

+×

′′

×−=

∫∫

jkj

)−

(200)

2н (;, )

(;,) (;,)(| |;,)

(,)

(;,) (| |;,) (;,)

(;,)(;,)

kQktt

dsG k t s Q j t s Q t s

dsG j t s Q t s Q k t s

dsG k t s w k t s

∂

′

−∞

′

−∞

⎛⎞

′

+−

⎜⎟

⎝⎠

⎧⎫

′

−−

⎪⎪

−=

⎨⎬

⎪⎪

′

−−

⎪⎪

⎩⎭

′

∫

jkj

(201)

Ранее мы встречали коэффициент L(k, j) в связи с теорией квазинормальности,

определенный соотношением (169). Фактически это тот самый коэффициент, который появляется

почти во всех перенормированных теориях второго порядка в изотропном случае.

Теория Кречнана DIA рассматривалась как большое продвижение вперед, как

существование физически осмысленного модельного представления, так как при интегрировании

по времени вперед она давала гарантированно положительный спектр, устраняющий катастрофу,

связанную с гипотезой квазинормальности.

Кречнан показал, что уравнения DIA обладают свойством сохранения энергии в

нелинейных взаимодействиях; при применении к ансамблям в состоянии абсолютного равновесия

эти уравнения дают равнораспределенные решения (т. е. дисперсия скорости не зависит от

волнового числа) наряду с флуктуационно-диссипативным соотношением (т. е. функция отклика

равна дисперсии как функции от времени). Как отмечал Кречнан, это дает статистическую основу

для переноса энергии от сильно возбужденных мод к слабо возбужденным модам. В реальных

случаях, когда жидкость обладает конечной вязкостью, это означает перенос энергии от малых

волновых чисел к большим.

Однако в случае больших чисел Рейнольдса модель DIA в инерционной области давала

спектр, пропорциональныый k

–3/2

, а не экспериментально подтвержденный k

–5/3

спектр

Колмогорова. Этот результат стимулировал поиски теории, способной предсказывать

колмогоровский спектр, который бы сохранял лучшие черты модели DIA. Кроме того, этот

результат стимулировал также интерес к исследованию воздействия больших вихрей на

декоррелирующий процесс (sweeping), обусловленный мелкими вихрями (см. обсуждение далее).

Как было отмечено ранее, формулировка проблемы с помощью характеристических

функционалов (или через распределение вероятности) математически эквивалентна формулировке

проблемы с помощью моментов. Однако в первом случае линейность исходных уравнений дает

некоторые преимущества, которые были использованы Эдвардсом в смелой попытке применить

теорию броуновского движения.

Следуя работе Эдвардса (1964), определим турбулентный ансамбль заданием

взбалтывающей силы. Примем, что взбалтывающая сила является случайной с

мультидисперсионным нормальным распределением, автокорреляция которой дается выражением

(138), чтобы быть уверенным в полной некоррелированности силы по времени. Усредненная

функция распределения вероятностей флуктуирующей скорости (P) получается с помощью

усреднения по ансамблю, определяющему распределение вероятностей взбалтывающей силы, что

позволяет получить уравнение для P. Это уравнение является обобщением уравнения Лиувилля,

при использовании которого возникают нетривиальные проблемы из-за того, что взбалтывающая

сила явно входит в это уравнение. Эта проблема аналогична вычислению перекрестной

корреляции скорости и силы, которую мы рассматривали ранее. Более общая трактовка этой точки

зрения [Эдвардс, 1964; Новиков 1965] приводит к следующему уравнению для P:

бвг в г

щ() н ()

()

() () ( ) 0.

()

kkuP

Muu

∂

⎡⎤

+−

⎢⎥

−

⎣⎦

−−

∑

kjkj

(202)

Это уравнение должно быть решено приближенно, для чего мы сначала запишем его в

упрощенной форме:

VPP−=L

, (203)

где определение вида операторов и V производится сравнением с предыдущим выражением.

При этом мы проведем лямбда-разложение, представив функцию распределения P в виде

01 2

лл ...PP P P=+ + +

(204)

0P =L

, (205)

где вид должен быть определен.

Определим теперь , причем сделаем это так, чтобы P

≅ P. Мы проведем это в два этапа.

Сначала добавим и вычтем из правой части уравнения (203). Затем припишем порядок λ

выражению VP, так как этот член имеет существенно тот же смысл, что и нелинейность в

уравнениях Навье–Стокса. Для корректного определения мы предположим также, что

имеет порядок λ

(−LL)P

. Затем, помня о том, что параметр λ в окончательном результате

полагается равным единице, получим уравнение

лV л ()PP P−− −=LLL

, (206)

которое является основой для пертурбативного разложения.

На этой стадии Эдвардс предположил, что спектр силы W(k) и скорость затухания мод из-

за вязкости могут быть заменены на

() () (),

щ() н (),

dk Wk sk

kkrk

(207)

где s(k), r(k) выражают влияние нелинейности. С физической точки зрения это правдоподобный

шаг, так как можно утверждать, что для любой моды

нелинейное взаимодействие возникает за

счет того, что привносится модами с меньшими и передается модам с большим . Фактически

уравнение (207) представляет одновременную ренормализацию взбалтывающей силы и вязкости.

Перенормировка оператора достигается при этом за счет добавления членов, содержащих

k k

sk rk(),()

()

щ() () ()

()

ku dk

∂

=×

⎡⎤

×+

⎢⎥

−

⎣

∑

⎦

(208)

с вычитанием соответствующих членов, позволяющих получить корректирующий оператор

−LL

С оператором нулевого порядка, заданного соотношением (208), уравнение (205) для

распределения основного порядка, как легко показать, имеет решение

бб

() ( )

exp

()

⎧⎫

−

⎪⎪

=−

⎨⎬

⎪⎪

⎩

⎭

∑

, (209)

где N – это приближенная нормализация, s(k), r(k) удовлетворяют соотношению

2щ()() ()kqk dk=

, (210)

а второй момент скорости дается выражением

бб

0 бб

2р

() ( )

() () ( )д ().

Pku u

⎛⎞

−=

⎜⎟

⎝⎠

=−

∫

kkuk

(211)

Коэффициенты в разложении P должны быть найдены из сравнения членов одинакового

порядка по λ. Обращение оператора нулевого порядка осуществляется с помощью разложения по

его собственным функциям. Если P

, P

, … найдены, то следствием уравнения (211) является

результат

бб 24

() ( )д ()[ ...] 0uu PP−++

∫

kkuk =

, (212)

в котором члены нечетного порядка не вносят вклада из-за симметрии.

Вычисление этого условия до второго порядка приводит к уравнению энергии

() 2н ()

(,)(| |){() ()}

щ() щ() щ(| |)

Wk kqk

dL q q j qk

−=

−−

=−

++−

∫

jkj k j

(213)

и отклика

(,)(| |)

щ() н

щ() щ() щ(| |)

dL q

−

++−

∫

jkj k j

. (214)

Эти уравнения являются уравнениями второго порядка по взаимодействию, аналогично

соответствующему результату для модели DIA, соотношения (200) и (201). Но в

противоположность DIA они не зависят от времени. Кречнаном показано, что две теории можно

связать, предполагая, что в модели DIA временная зависимость может быть аппроксимирована

экспонентой со скоростью затухания мод ω(k), с последующим интегрированием по

промежуточным временам. Этим способом он нашел, что уравнение энергетического баланса

сводится к уравнению Эдвардса, а уравнения для отклика принимает вид

(,)(| |)

щ() н

щ() (| |)

dL q

−

+−

∫

kj k j

. (215)

Следует отметить, что уравнение отклика в модели DIA имеет только два характерных времени,

появляющиеся в знаменателе, в то время как EFP уравнение имеет три.

Эдвардс (1965) показал также, что из рассмотрения консервативных свойств уравнения

EFP в пределе бесконечного числа Рейнольдса следует ряд интересных результатов.

При стремлении к этому пределу мы предположим, что вязкость стремится к нулю таким

образом, чтобы скорость диссипации оставалась постоянной. Из определения колмогоровского

диссипативного волнового числа в соответствии с (147) следует, что диссипация сдвигается в

область бесконечных волновых чисел и в этом пределе стремится к дельта-функции на

бесконечности.

В общем случае спектр накачки W(k), который является произвольным, должен быть

выбран в виде функции, сконцентрированной вблизи начала координат в k-пространстве так,

чтобы универсальное поведение могло развиться при больших волновых числах. Однако если мы

уменьшаем вязкость, то становится легче возбуждать моды при малых волновых числах, и в

пределе оказывается, что мы можем возбуждать систему при k = 0, т. е. накачка энергии может

быть задана тоже в виде дельта-функции, но на этот раз в начале координат.

При осуществлении этих условий, когда энергия подводится в точке k = 0 с помощью

внешней взбалтывающей силы и откачивается в точке k = ∞ за счет диссипации, колмогоровский

спектр можно ожидать во всей области волновых чисел, так что степенной закон для спекральной

плотности, определеннный в безразмерных переменных, дается выражением (152). Аналогичным

образом анализ размерностей дает нам скорость затухания мод в виде

1/3 2 /3

щ() веkk=

, (216)

где β – некоторая постоянная, подлежащая определению. На основе этого Эдвардс показал, что

уравнения (213) и (214) сводятся к

11/3 11/3 11/3

2/3 2/3 2/3

б (,)| | { }

8рв

4р

д() д(),

dL k j

−− −

−

−−

⎛⎞

⎜⎟

++−

⎝⎠

=−−∞

∫

jkjkj

(217)

1/3 11/3

1/3 2/3

2/3 2/3 2/3

бе (, )

ве .

4рв

dL j

−

++−

∫

jkkj

(218)

В принципе эти два уравнения должны были бы определять и константы α и β, но появляется

затруднение в уравнении для отклика, которое оказывается неинтегрируемым из-за расходимости

при j = 0. Это знаменитая инфракрасная расходимость теории турбулентности.

Хорошо известный метод самосогласованного поля был применен к проблеме

турбулентности Герингом (1965, 1966). Метод был похож во многом на метод Эдвардса и

приводил (в своей не зависящей от времени форме) к EFP уравнению энергии (213) и, что

любопытно, к независящему от времени DIA уравнению (215) для отклика, а не EFP форме (214).

В своей последней, зависящей от времени, формулировке метод самосогласованного поля Геринга

дает DIA уравнения.

Недостаток места не позволяет рассмотреть эту элегантную теорию достаточно подробно,

она рассмотрена в работе [МакКомб, 1990]. Более поздние попытки теорий самосогласованного

поля в турбулентности в зависимости от основных предположений приводили либо к уравнениям

Геринга [Балеску и Сенаторски, 1970], либо к DIA уравнениям [Питиан, 1969]. Одно из очевидных

приложений всего этого состоит в том, что перенормировочные теории первого рода являются

некоторой формой теорий самосогласованного (или среднего) поля. Так как они не совместимы с

колмогоровским спектром, то отсюда следует, что колмогоровское распределение вряд ли

является следствием теории самосогласованого поля вопреки стремлению некоторых

комментаторов проводить слишком далеко аналогию с фазовыми переходами второго рода и

утверждать, что это так и есть [Сиггиа, 1977].

Из подобия соотношений (214) и (215) легко видеть, что неудача DIA (по крайней мере, в

ее независящей от времени форме) с колмогоровским распределением, также, как и EFP, может

быть объяснена инфракрасной расходимостью. Однако в общем случае неудача DIA может быть

связана с ее внутренней неспособностью различать эффекты однородной конвекции и процессы

генерации внутренних напряжений, сопровождающиеся переносом энергии. В результате теория

не может разделить эффекты энергосодержащих (малых) волновых чисел от динамики в

инерционной области [Кречнан, 1964b]. Помимо этого интересно отметить, что этот анализ связан

с гипотезой «случайного свиппинга», которая утверждает, что затухание эйлеровской

двухточечной корреляции на малых масштабах определяется крупномасштабным свиппингом с

временем декорреляции (kU)

–1

, где U – некоторая характерная скорость в области

энергосодержащих волновых чисел. Использование численных методов для исследования

случайного свиппинга стало в настоящее время весьма популярным, и мы сошлемся здесь на ряд

ведущих работ в этом направлении [Чен и Кречнан, 1989; Нелкин и Табор, 1990; Санда и

Шанмугусандаран, 1992; Гото и др.), замечая, что, по крайней мере, в области от малых до

умеренных чисел Рейнольдса результаты подтверждают эту гипотезу.

Упомянутый выше анализ Кречнана (1964), направлен на общую формулировку принципа

стохастической галилеевой инвариантности, которой должна удовлетворять теория. Конечно,

тривиальным является утверждение о том, что уравнения Навье–Стокса и теории, основанные на

них, удовлетворяют обычной форме инвариантности Галилея [МаКомб, 1990]. Но совсем не

очевидно, что теории удовлетворяют более общему стохастическому условию, и, кроме того, не

ясно, что это условие можно соответствующим образом сформулировать.

Тем не менее Кречнан получил, что не только DIA, но также все эйлеровские

двухвременные корреляционные теории должны с неизбежностью нарушать это условие и,

следовательно, быть неспособными подтверждать колмогоровскую картину динамики в

инерционной области. Как мы увидим далее, это чрезмерно пессимистическая точка зрения.

Рассмотрим только начальные стадии альтернатив Кречнана, состоящие во введении новой

координатной системы, которая имеет некоторое отношение к лагранжевым координатным

системам, описанным выше. Результирующие уравнения необычайно сложны, более того, не

зависимо от того, что они с очевидностью дают колмогоровский спектр, они требуют некоторого

упрощения, поэтому существует несколько различных форм этих уравнений. Полное

рассмотрение проведено в работе [МакКомб, 1990], здесь же дано краткое введение.

При исследовании трудностей DIA Кречнан (1964) заметил, что использование обрезания

по волновым числам устраняет ложные конвективные эффекты и что это эквивалентно

представлению уравнений Навье–Стокса в квази-лагранжевой системе координат. Он

переформулировал DIA уравнения в названные им координаты «лагранжевых траекторий»

[Кречнан, 1965]. Главным шагом в этой процедуре является введение обобщенной скорости

u(x, t|s), которая определена как скорость жидкой частицы, которая была в точке x в момент

времени t, измеренная в момент времени s. Два различных времени известны как

t = время маркировки,

s = время измерения.

Ясно, что обобщенная скорость должна удовлетворять двум предельным условиям:

(, |) (,)tt t=ux ux

(219)

и для фиксированных значений (x

, t

)

00 0

(,|) (,)ts V s=ux x

, (220)

где V – поле лагранжевой скорости, определенной выше. Фактически зависимость от t является

эйлеровской характеристикой, в то время как s – лагранжевой.

Когда t = s, обобщенная скорость является чисто эйлеровской и удовлетворяет уравнениям

Навье–Стокса. В противном случае можно показать, что обобщенная скорость удовлетворяет

уравнению

(,) (, |) 0tts

∂

⎡⎤

⎢⎥

⎣⎦

ux ux

(221)

Поэтому при t = s обобщенная скорость удовлетворяет условию несжимаемости, чего нет в случае

нарушения этого условия. Кречнан использовал это обстоятельство для разделения обобщенной

скорости на соленоидальную и незавихренную части, к которой DIA не может быть применена.

Дальнейшие пояснения могут быть найдены в работах Кречнана (1965, 1977) и Кречнана и

Геринга (1978). Как мы уже отмечали ранее, результирующие усложнения являются крайне

значительными, и существует несколько направлений, по которым можно честно следовать

исходной постановке задачи. К тому же недавно Базденков и Кухарин (1993) указали, что

результат зависит от того, что принято за исходное поле: поле скорости, поле напряжений или

поле завихренности. Несомненно, надо отметить, что, пользуясь этой теорией, Кречнан (1966)

опубликовал теоретическое значение спектральной константы Колмогорова α = 1,77, которое

находится в пределах области экспериментальных значений.

Наконец, ради полноты отметим неэйлеровское перенормированное разложение Хорнера и

Липовски (1979), в котором был использован формализм Мартина, Сиггиа и Роуза для построения

галилеево-инвариантного разложения, а также метод Канеды (1981), в котором предложен вариант

кречнановской формулировки на основе лагранжевых траекторий с использованием производных

по измеримому времени, а не по маркировочному. Эти теории также приводят к хорошему

предсказанию константы Колмогорова с α = 1,72 [Канеда, 1986].

Были сделаны две попытки решения EFP теории. Эдвардс и МакКомб (1969) получили

уравнения для отклика, максимизируя турбулентную энтропию. Вторая попытка была основана на

гипотезе локальности переноса энергии [МакКомб, 1974; 1976] и приводила к LET теории, которая

будет рассмотрена в следующем пункте. Здесь мы будем следовать Эдвардсу и МакКомбу (1969),

которые показали, что энтропия, интерпретируемая как отрицательная информация, пригодна для

описания некоторых систем, которые не находятся в состоянии термодинамического равновесия.

Так если общий вид [Шеннон и Вивер, 1949] задать выражением

lnSP

=−

∫

, (222)

где κ – постоянная, а интегрирование проводится по всем переменным системы, то для P,

являющимся решением уравнения (202) в виде λ-разложения (204), получим энтропию

турбулентности в виде

012 012

00 101

( ...)ln( ...)д

ln дл д (л ),

SPPP PPP

PP PPP O

−

=− + + + + + + =

−− +

∫

∫∫

(223)

где нечетные по маркировочному параметру члены исчезают при интегрировании благодаря

симметрии, член второго порядка P

не вносит вклада из-за наложенного на него условия (212).

Следует отметить, что мы положили константу κ = 1, так как она не существенна для вычислений.

Коэффициент P

задан соотношением (209). Для определения P

сошлемся на результаты

Эдвардса (1964), Эдвардса и МакКомба (1969) или МакКомба (1990). Этот член является членом

первого порядка по нелинейности и суть функционал от q(k) и ω(k).

Результирующее выражение для члена второго порядка для турбулентной энтропии имеет

вид

2р 1

ч() ()

2р [(,,)()() (,, )()()]

()[щ() щ() щ()]

Sqk

LqjqlLqkqj

qk k j l

⎛⎞

=−−

⎜⎟

⎝⎠

−

⎛⎞

−

⎜⎟

⎝⎠

∑

kjl

kjl ljk

(224)

где маркирующий параметр положен равным единице, а выражение L(k, j, l) связано с

выражением (169) соотношением

(,,) (,)д()LL=+kjl k j k j l+

. (225)

Заметим, что первый член в правой части (224) есть число степеней свободы системы и, поскольку

оно постоянно, не вносит вклада при дифференцировании.

Теперь, исходя из EFP теории, мы видим, что уравнение энергии дает одно соотношение

для двух неизвестных q(k) и ω(k), а варьирование энтропии S(q(k), ω(k)) по ω(k) даст нам второе.

Но для того чтобы сделать это, мы должны принять во внимание, что существующее соотношение

между q(k) и ω(k) действует как ограничение на вариацию. В соответствии с этим мы и должны

записать вариационный принцип, который дает нам второе соотношение в виде

ддд()

дщ() д () дщ()

SSqj

kqjk

⎡⎤

⎢⎥

⎣⎦

∑

, (226)

в котором коэффициент перед вторым членом в правой части уравнения может быть получен из

(210) в виде

д () () д ()

дщ() 2щ ()д()2щ()дщ()

qj dk dj

kkkjj

=− +

−

. (227)

Поскольку второй член в правой части уравнения потребовал бы огромных усилий для

своего вычисления, Эдвардс и МакКомб просто опустили его. Найдя вариацию S в соответствии с

(227), они получили новое уравнение для отклика. Для некоторого частного ω(A) оно имеет вид