Хлопков Ю.И., Жаров В.А., Горелов С.Л. Лекции по теоретическим методам исследования турбулентности

Подождите немного. Документ загружается.

12 12 2

н //

Ux uu x P∂∂−∂ ∂=∂∂

. (29)

Если мы сравним этот результат с уравнением (9), соответствующим случаю ламинарного

течения, то можем заметить, что в дополнение к замене мгновенных величин на их средние

значения появляется корреляция флуктуационных скоростей

〈 u

〉 , обычно называемая

напряжениями Рейнольдса, которая дополняет вязкий член и выражает дополнительное

сопротивление движению за счет флуктуаций.

Уравнение (25), описывающее баланс турбулентной энергии, можно еще применить к

случаю полностью развитого, стационарного среднего течения в плоском канале. Требуя

выполнения указанных ограничений, можно приравнять нулю производные по

t, x

, x

, а также

недиагональную корреляцию, содержащую

, и свести исходное уравнение сохранения энергии к

виду, приспособленному для описания развитого турбулентного течения в канале:

12 1 2

2 б 22

б,в

2 с

н (/) е

u u dU dx

ddx uu up

αβ

∂∂

−−

⎛⎞

−+

⎜⎟

⎝⎠

∑

(30)

В этом выражении отброшен член вязкой диффузии на том основании, что он мал по сравнению с

остальными членами почти во всей области, кроме пристеночной, как это следует из

экспериментальных данных.

Можно охарактеризовать турбулентный пограничный слой в жидкости, текущей около

твердой поверхности, с помощью масштаба длины и скорости, задав полную толщину слоя

δ и

скорость набегающего потока. Эти параметры известны под названием «внешних масштабов». Но

можно определить и «внутренние масштабы», которые необходимо использовать, если нам нужно

охарактеризовать структуру турбулентности. Для того чтобы обсуждать скейлинговое поведение в

сдвиговых течениях, необходимо ввести соответствующие внутренние масштабы.

Прежде всего обычно разделяют турбулентный пограничный слой на внутренний слой

(приближенно), расположенный в области 0

≤ x

≤ 0,2 δ, и внешний слой, ограниченный областью

0,2

δ ≤ x

≤ δ, где координата x

измеряется по нормали к поверхности: x

= 0 на поверхности и

~ δ на внешней границе пограничного слоя. (Следует заметить, что положение внешней

границы турбулентного пограничного слоя само по себе является случайной величиной, поэтому,

когда мы ссылаемся на нее, то подразумеваем среднее значение.) Такое разделение на слои

основано на экспериментальных наблюдениях, которые показывают, что величина полного

напряжения сдвига

, определенного соотношением (21), остается практически постоянной во

внутреннем слое и приближенно равна его значению

на поверхности (стенке).

Подобные рассуждения, относящиеся к пограничному слою на пластине в потоке

жидкости, могут быть перенесены на течение в канале. В таком течении постоянство величины

напряжения сдвига в подслое не является сильно выраженным свойством, но подразделение на

подслои все еще оправдано общей феноменологией.

Внутренний слой можно разделить на подслои по относительной величине вязких и

турбулентных напряжений. В данном случае уравнение (21) принимает простой вид

12 1 2 1 2

фсн / сdU dx u u=−

, (31)

в котором вязкий член определяется законом Ньютона по средней скорости деформации, а

турбулентная часть соответствует компоненте тензора напряжений Рейнольдса.

Около стенки граничное условие, накладываемое на скорости: {

, u

} → 0 при x

→ 0,

утверждает, что произведение

стремится к нулю при приближении к стенке. Поэтому на

стенке напряжение обусловлено только вязкими напряжениями и может быть записано в виде

фсн[/]

dU dx

, (32)

Теперь можно определить вязкий подслой как область вблизи стенки, в которой доминирует

первый член в правой части соотношения (31). Для больших значений

второй член в правой

части (31) становится доминирующим, поэтому эта область часто называется областью

постоянства турбулентного напряжения. Очевидно, что существует промежуточная область, в

которой оба члена имеют одинаковый порядок величины. Такая область называется переходной

(или, часто, буферным подслоем).

Физическую меру каждого из этих подслоев наиболее удобно выразить через так

называемые «внутренние переменные», которые могут быть введены следующим образом.

Анализ размерностей (подтвержденный экспериментом) показывает, что подходящим

масштабом скорости для внутренней области может быть величина

1/ 2

(ф / с)

u =

, (33)

в соответствии с которой масштаб длины внутреннего слоя определится как

«масштаб длины внутреннего слоя» =

ν / u

, (34)

где

– так называемая «вязкая скорость». Как будет видно из дальнейшего, u

имеет тот же

порядок, что и величина среднеквадратичной флуктуации скорости.

Используя соотношения (32) и (33), можно определить безразмерные переменные:

22ф

/ нxxu

11ф

/UUu

. (35)

Эти величины предназначены для измерения расстояний от стенки в единицах

ν/u

и для

малой вязкости приводят к растяжению пристеночной области.

Экспериментальные результаты (которые будут обсуждаться позже) позволяют

предложить следующую классификацию:

внутренний слой 0

≤ x

≤ 0,2 δ

внешний слой 0,2

δ ≤ x

≤ δ

При этом внутренний слой разделен на подслои следующим образом:

вязкий подслой 0

≤

≤ 5

переходный слой 5

≤

≤ 30

турбулентный слой

постоянного напряжения

> 30

Следует подчеркнуть, что характерные величины, принятые для

с целью ввести

классификацию слоев, различны у разных авторов. Это, безусловно, подчеркивает трудности в

установлении точных критериев установления границ между подслоями.

Феноменологические теории для среднего профиля скорости были подкреплены

экспериментальными наблюдениями, позволяющими проверить законы подобия в

рассматриваемых здесь ситуациях. Например, во внутренней области пограничного слоя

совокупность измерений средней скорости может быть сведена к универсальной форме:

Ufx

= ()

, (36)

которая известна как «закон стенки».

Предполагается, что стенка имеет гладкую поверхность. Если высота (как-либо

определенная) неоднородностей на стенке меньше, чем толщина вязкого подслоя, то говорят, что

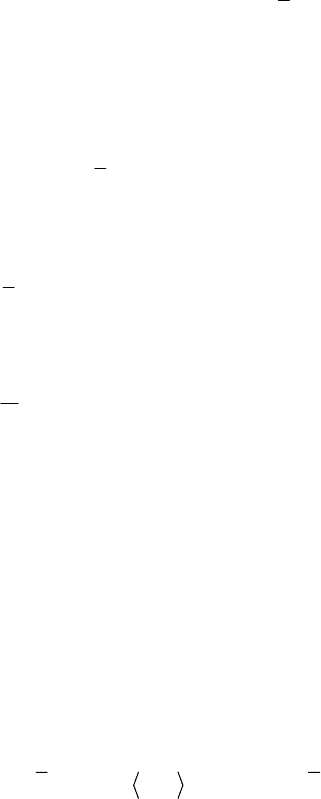
стенка «гидравлически гладкая» и выполняется закон подобия (36). Если высота неоднородности

больше толщины вязкого подслоя, то она определяет масштаб внутренней области.

С другой стороны, для внешней области эксперимент дает самосохраняющуюся форму

профиля вида

(/д)UU gx

∞

−=

, (37)

которая известна под названием «закон дефекта скорости».

Функции f и g могут быть определены (по крайней мере, для большей части пограничного

слоя), если потребовать здесь, чтобы существовала область, где обе формы (или даже их первые

производные) непрерывны. Подробные пояснения могут быть найдены в книге [Хинце, 1975].

Результат известен: функции

f и g должны быть логарифмами, а уравнение (37) принимает вид

UAx

=ln( ) B+

(38)

где

A и B – постоянные, которые должны быть определены из сравнения соотношения (38) с

экспериментальными результатами.

Этот логарифмический профиль средней скорости прекрасно подтвержден

экспериментально, причем до такой степени, что приобрел статус закона природы в области

динамики жидкости. К сожалению, как мы еще увидим, этот закон не выполняется вблизи стенки

и во внешней части пограничного слоя. (Совершенно очевидно, что соотношение (38) не может

удовлетворять граничному условию

(0)Ux 0

Однако можно установить предельную форму средней скорости на стенке, рассматривая

уравнение (31) для полного напряжения сдвига в пределах вязкого подслоя. Требуя, чтобы полное

напряжение было постоянным в этой области (

= τ

), и чтобы напряжения Рейнольдса

стремились к нулю, получим

ф /сн /

dU dx=

, . (39)

≤

Интегрируя это соотношение по

и используя (33), получим

1 ф 2

/ нUux=

, (40)

или в безразмерных переменных

, (41)

при этом константа интегрирования положена равной нулю для того, чтобы удовлетворить

граничному условию на стенке. Этот линейный закон применим только к вязкому подслою и

получил достаточное экспериментальное подтверждение.

Хотя уравнения Рейнольдса для средней скорости не могут быть решены, можно

проинтегрировать их для получения нескольких полезных результатов, относящихся к сдвиговым

течениям. В частности, мы обсудим двумерное течение в канале, образуемом добавлением второй

пластины, параллельной плоскости (

, x

), расположенной при x

= 2a над плоскостью x

= 0. Вниз

по течению на значительном удалении от входа в канал, где оба пограничных слоя сливаются

вместе, турбулентное течение будет хорошо развито, поэтому уравнения Рейнольдса сведутся к

уравнению (29).

Перепишем уравнение (29), заменяя частные производные на обыкновенные; получим

12 12 2

н //(1/с)/dU dx d uu dx dP dx−=

. (42)

Интегрирование каждого члена уравнения по

дает

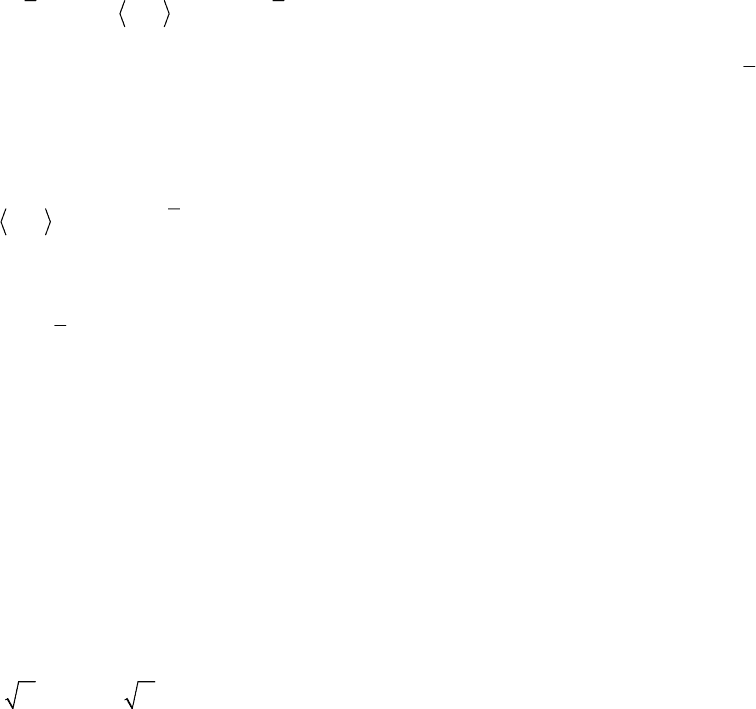
12 12 2 11

сн / с ()/фdU dx u u x a dP dx−=− =

, (43)

в котором последняя операция получена с использованием уравнения (31) и условий

/0dU dx

〈 u

〉 = 0 при x

= a (центральная линия канала).

Для значений

, расположенных достаточно далеко от стенок канала, можно пренебречь

вязкими напряжениями и записать напряжения Рейнольдса в виде

12 2 1 12

с ()/фu u x a dP dx=− − =

. (44)

С другой стороны, на стенке (т.е. при

= 2a) имеем важное соотношение

ф /

adP dx=

, (45)

которое подтверждает простой метод определения сдвигового напряжения на стенке с помощью

двух легко измеримых величин.

Кроме того, можно ввести коэффициент турбулентного сопротивления

f с помощью

соотношения

2ф / с

, (46)

где

U – среднемассовая скорость.

Наконец, для полноты следует заметить, что существует эмпирический закон для

коэффициента сопротивления в канале. Он имеет вид [Годстейн, 1938; с. 338].

1/ 4log( ) 0,4fRf=−

, (47)

где f – коэффициент сопротивления, и называется законом Прандтля–Кармана.

Существует огромное количество данных, относящихся к турбулентности, большая часть

которых получена много лет назад. Заинтересованный читатель может получить прекрасное

впечатление о предмете, если он заглянет в книгу «Modern Developments in Fluid Dynamics»

[Голдстейн, 1938; в двух томах]. Не стоит комментировать скорость развития предмета

исследований, чтобы понять, что слово «современный» не такое уж здесь неуместное. Чтобы

картина была достаточно содержательная, рассмотрим только несколько исследований. Мы

ограничим внимание на течении в канале.

Для того чтобы дать представление о течении в канале, обратимся к работам Никурадзе

(1932, см. [Голдстейн, 1938]), Лауфера (1954) и Лоуна (1971), которые связаны с исследованиями

течения в трубах круглого сечения. Результаты для других форм канала – плоских течений – не

сильно отличаются от рассматриваемых ниже. Но для полноты будут рассмотрены работы

Лауфера (1951), Хуссейна и Рейнольдса (1975), а также Креплина и Экельмана (1979),

посвященные исследованиям в каналах.

Наконец, прежде чем вернуться к обсуждению экспериментальных результатов последнего

времени, нам придется переопределить координатную систему для течений с другими

геометриями. Для течений в каналах

– координата в продольном (осевом) направлении, x

–

расстояние от стенки в радиальном направлении,

– азимутальная.

На рис. 2 показано распределение средней скорости в трубе для трех сильно

отличающихся друг от друга чисел Рейнольдса. Результаты взяты из работ Никурадзе (1932) и

являются достаточно хорошей характеристикой турбулентности с резким изменением профиля

скорости около стенки и более пологим профилем вблизи ядра. Ясно, что такое поведение

профиля скорости становится более выраженным по мере роста числа Рейнольдса.

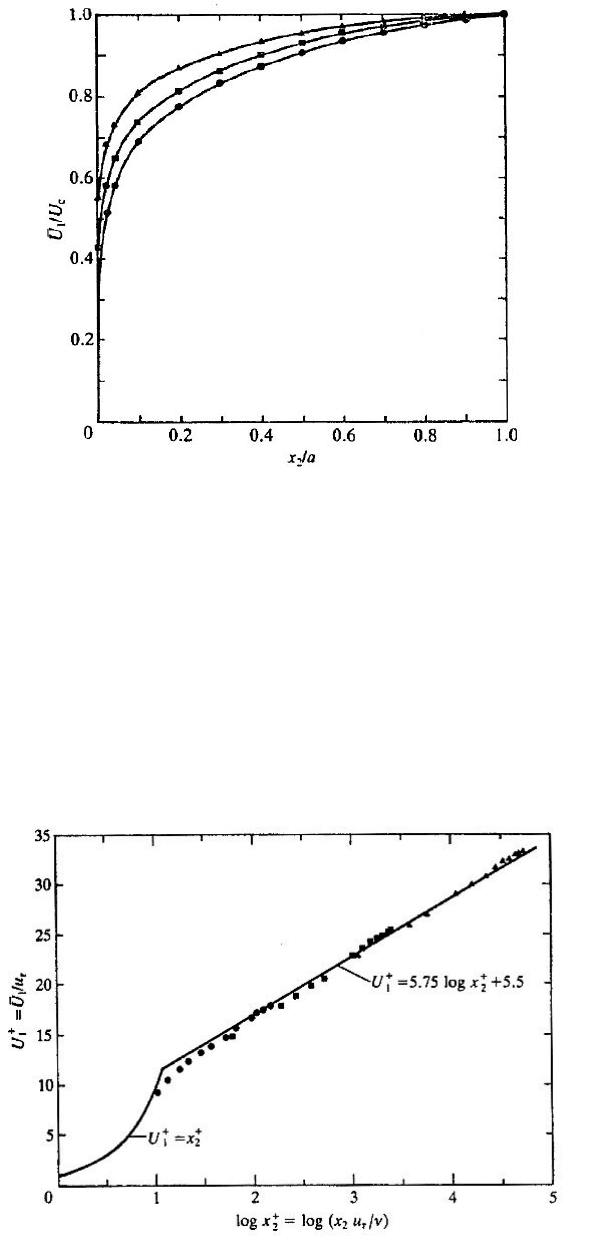
Рис.2. Распределения средней скорости для течения в трубе

при различных числах Рейнольдса:

● – 4×10

, ■ – 1,1×10

, ▲ – 3,2×10

Стремление формы профиля к универсальному «закону стенки» показано на рис. 3, на

котором сведены воедино все три предыдущие совокупности экспериментальных точек.

Поскольку абсцисса

на графике отложена в логарифмическом масштабе (логарифм по

основанию 10), прямая линия указывает на удовлетворительную логарифмическую зависимость,

которой удовлетворяет большая часть данных.

Рис. 3. Логарифмическое распределение средней скорости для

течения в трубе: универсальная форма закона в пристеночных

переменных (обозначения те же, что и на рис. 2)

Этот результат подтвержден многочисленными исследованиями (например, см.

[Голдстейн, 1938], [Хинце, 1975]). Это говорит о том, что распределение скорости, задаваемое

соотношением (38), находится в хорошем согласии с экспериментальными данными, за

исключением тех, которые относятся к области, непосредственно примыкающей к стенке. Однако

значительно меньше согласия проявляется в отношении значения констант

A и B. На рис. 3

прямая линия соответствует выражению

5, 75log( ) 5,5Ux

и, переходя к натуральным логарифмам, получим, что

A = 2,5 и, следовательно, константа фон

Кармана равна

k = 0,4. Но даже в рамках приведенных здесь данных ясно, что экспериментальный

разброс допускает и другие значения констант

A и B.

В противоположность этому средний профиль скорости в вязкой подобласти является

строгим результатом. И хотя мы не представили ни одной экспериментальной точки в этой

области на рис. 3, линейный закон также проверен экспериментально (последние данные из этой

области см. в работе [Бэйквелл и Ламли, 1967]).

Для определения величин в турбулентном течении обратимся к классическим измерениям

Лауфера (1954), который использовал технику проволочных термоанемометров для получения

трех компонент флуктуирующей скорости для течения воздуха в канале. На рис. 4 представлены

среднеквадратичные скорости

′, u

′, деленные на скорость u

, определенную по трению на

стенке, в зависимости от

/a для двух различных чисел Рейнольдса R = 50 000 и R = 500 000.

Очевидно, что каждая среднеквадратичная компонента удовлетворительно коррелирует с

, за

исключением области вблизи стенки.

Другие точки, как можно заметить, содержат несоответствие между компонентами в

большинстве течений, благодаря тенденции к их возрастанию в направлении стенки и стремлению

к одному пределу на оси трубы. Обсуждение этих аспектов будет отложено до следующего

пункта, в котором будет рассмотрен процесс производства и переноса турбулентности.

Рис. 4. Радиальное распределение трех среднеквадратичных компонент скорости для турбулентного течения

в трубе: u

′/u

⎯ , u

′/u

⎯ − ⎯ , u

′/u

- - -

На рис. 5 показано распределение величин

〈 u

〉 /u

, 〈 u

〉 / u

′u

′. Первое из них – это

отношение напряжений Рейнольдса к напряжениям на стенке; данные подтверждают линейную

зависимость, предсказанную соотношением (42). Вторая величина – это коэффициент корреляции,

который равен приблизительно 0,4 независимо от точки.

Сначала мы объясним уравнение сохранения энергии для флуктуационных скоростей, т. е.

уравнение (25). Обращаясь к четвертому члену правой части уравнения, мы назвали его членом

производства, так как он выражает преобразование энергии от среднего поля к флуктуирующему и

интерпретируется поэтому как скорость генерации турбулентности. Рассмотрим этот член в

условиях стационарного хорошо развитого течения в канале. Уравнение (30) есть уравнение (25),

переписанное и приспособленное к описанию течения в канале. Член производства энергии теперь

появляется в виде первого члена в левой части уравнения (30) и имеет вид

12 1 2

/u u dU dx−

. (48)

Рис. 5. Радиальное распределение напряжения Рейнольдса

и коэффициента корреляций для турбулентного течения в трубе:

〈 u

〉 /u

⎯, 〈 u

〉 /u

′u

′ - - -

Теперь мы в состоянии понять некоторые качественные особенности результатов,

относящихся к среднеквадратичным величинам скоростей, рассмотренных ранее. Из рассмотрения

уравнений (24) и (48) можно сделать следующие выводы:

(а) кинетическая энергия среднего течения преобразуется только в флуктуации продольной

скорости

〈 u

〉 , поэтому не удивительно, что u

′ больше, чем остальные компоненты u

′, u

′;

(б) радиальная и азимутальная компоненты

′, u

′ возбуждаются за счет инерционной

передачи энергии от

′ посредством тройных корреляций или, конкретнее, благодаря члену,

содержащему флуктуации давления.

(в) скорость генерации 〈 u

〉 будет очень большой около стенки, где велики и напряжения

Рейнольдса и средний градиент скорости. Эта скорость должна быстро падать при удалении от

стенки. Таким образом, роль тройных корреляций состоит в переносе энергии в радиальном

направлении (стремление к однородности) и преобразовании энергии от

〈 u

〉 к 〈 u

〉 и 〈 u

〉

(тенденция к изотропии). Это подтверждается результатами, приведенными на рис. 4, которые

показывают, что среднеквадратичные компоненты приближенно равны и относительно однородны

около оси трубы, где член генерации турбулентности равен нулю.

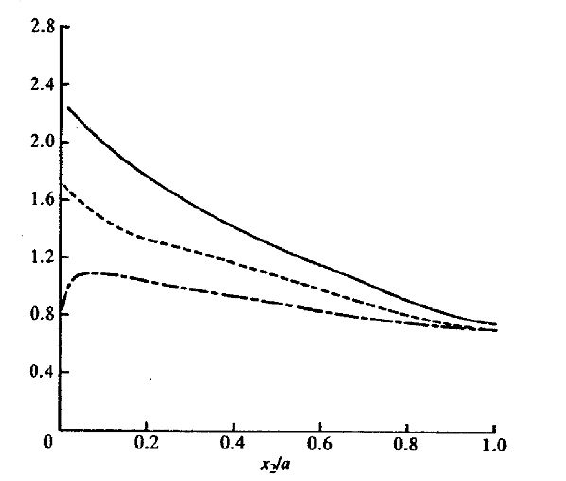
Можно рассматривать баланс энергии, вернувшись к уравнению (25). Лоун (1971) измерял

величины отдельных членов в уравнении. Его результаты приведены на рис. 6. Измерение

генеративного члена весьма доступно, в то время как измерение скорости диссипации

представляет большие трудности, так как подразумевает измерение девяти независимых

компонентов флуктуирующего тензора скоростей изменения напряжения. На рис. 6 кривая

диссипации энергии была получена вычислением разности между генерацией и инерциальной

трансформацией (или диффузией). К сожалению, эта процедура страдает от того, что вклад от

флуктуаций давления в диффузию не может быть измерен непосредственно и должен быть оценен

другим способом с потерей точности.

Лоун также определил скорость диссипации двумя другими методами, которые были

основаны на предположении локальной изотропии в области малых масштабов, которые больше

всего ответственны за диссипацию. Далее эти методы не обсуждаются, поскольку они содержат

элементы, лежащие очень далеко от содержания этого курса. Однако из рис. 6 ясно, что все три

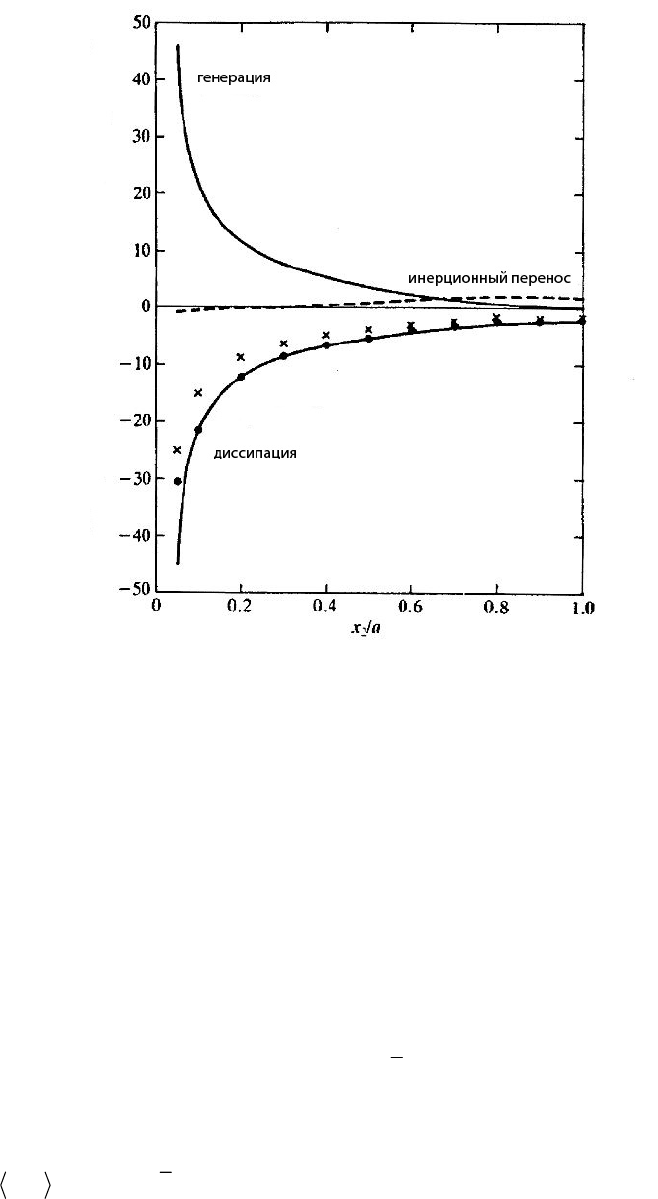
метода определения скорости диссипации достаточно хорошо согласуются друг с другом, поэтому

мы относимся к этим результатам как к достаточно убедительному доказательству выполнения

уравнения баланса турбулентной энергии.

Рис. 6. Баланс турбулентной энергии в ядре потока в трубе

(Лоун, 1971)

Мы рассмотрим традиционные феноменологические теории турбулентности, хотя можно

доказать, что первая – это общее предположение, а вторая – есть просто метод его реализации.

Начиная с ранних исследований турбулентности, было сделано много попыток согласовать

идеи, лежащие в основе кинетической теории газов с представлениями о свойствах континуума

(особенно со свойством завихренности и вихревого движения в целом), встречающихся в

макроскопическом движении жидкости. В результате многие теории турбулентности

основывались на аналогии между хаотическим движением вихрей и случайном движении молекул

в разреженных газах. Модель длины смешения (см., например, [Шлихтинг, 1968], [Хинце, 1975])

хорошо известна и дает нам интересный пример, который мы здесь обсудим. Мы начнем с

рассмотрения связанного с этими представлениями понятия эффективной вихревой вязкости.

Представление о том, что коллективное движение вихрей может быть заменено

коэффициентом вязкости, очень привлекательно. Традиционно оно вводится по аналогии с

известными результатами кинетической теории (например, как в уравнении (8)):

среднее вязкое сдвиговое напряжение =

сн /dU dx

Можно попытаться представить турбулентное сдвиговое напряжение в аналогичной форме

12 2 1 2

ссн() /

uu x dU dx−=

, (49)

где

) – это кинематическая вихревая вязкость. Вопреки тому, что провозглашение такой

аналогии было очевидно даже для ранних исследователей турбулентности, эта гипотеза все еще

привлекает большое внимание. Позднее мы рассмотрим дополнительные подтверждения этой

идеи о вихревой вязкости на основе недавних ренормгрупповых исследований, которые будут

даны с некоторыми ограничениями. На данной стадии мы просто отметим, с критической точки

зрения, что в течении, где

dU dx

и 〈 u

〉 обращаются в ноль одновременно в некоторой

точке, вихревая вязкость (определенная соотношением (49)) может быть либо нулем, либо

бесконечностью в некоторых точках течения. Если же мы преследуем аналогию с

континуальными механизмами, а не кинетической теорией, то очевидно, что «конститутивные

соотношения» для турбулентности в общем случае должны быть существенно более сложными,

чем чисто «ньютоновское», определяемое соотношением (49).

Модель длины смешения является более амбициозной попыткой построить аналогию с

кинетической теорией. Мы начнем с напоминания о том, что напряжение сдвига Рейнольдса

ρ〈 u

〉 – это поток x

- компоненты импульса в направлении x

. Прандтль предположил, что этот

импульс переносится дискретными порциями жидкости, которые перемещаются в направлении

на расстояние

l без взаимодействия друг с другом (т. е. предполагается, что их импульс

сохраняется на длине

l), а затем перемешиваются с жидкостью в новом месте. Ясно, что длина l,

называемая длиной смешения, играет в этом процессе роль длины свободного пробега.

Существенным в этом анализе является следующее. Жидкий элемент

dV переносится из

точки

в точку x

+ l с помощью флуктуации скорости u

. При этом переносится импульс в

другую точку благодаря разности между

()

Ux l

(+ )

. В результате изменяется импульс в

направлении

и, следовательно, изменяется скорость u

в направлении x

. Это можно выразить

следующим образом:

11212

сс[() ( )]

с (/)

udV U x U x l dV

ldU dx dV

=−+

=−

(50)

с точностью до первого порядка по

l , следовательно

u ldU dx

=−(/

)

. (51)

Заметим, что, если

является возрастающей функцией x

, жидкие частицы, движущиеся в

направлении положительных

(т. е. в направлении, соответствующем положительным

флуктуациям

), вызывают отрицательную флуктуацию в скорости u

. Таким образом,

напряжение Рейнольдса будет отрицательно, поэтому корреляцию можно записать, используя

среднеквадратичные скорости, в виде

12 1212 1

uu R uu C u

′′

=− =−

, (52)

где

– коэффициент корреляции. Следующий шаг следует из экспериментальных наблюдений,

которые показывают, что

′ имеет тот же порядок величины, что и u

′ в подслое, где напряжение

постоянно. Выразив через константу

C коэффициент R

, получим из формулы (51)

12 1 2

сс(/)uu l dU dx=−

, (53)

где константа

C теперь уже вошла в определение l.

На этом этапе нам необходимы дальнейшие предположения, а именно:

(а) в подслое постоянного напряжения можно положить

= τ

;

(б) для

> 5 можно пренебречь вязким членом в сдвиговом напряжении;

(в)

l = k x

, где k известна как константа Кармана.

После этого, воспользовавшись уравнениями (31) и (53), получим

12 1 2

ф / с (/)

uu l dU dx=− =

, (54)

откуда, с учетом уравнения (32),

22 2 2

212 ф

(/)kx dU dx u=

. (55)

Наконец, извлекая корень квадратный из правой и левой частей уравнения и интегрируя по

получим профиль скорости в виде

1 ф 2

(/)ln()Uukx= D+

, (56)

где

D – константа интегрирования. Этот результат можно сшить с линейным профилем (см.

уравнение (41)), выбрав соответствующим образом константу

D. В результате получим, что

логарифмический профиль, задаваемый соотношением (56), удовлетворяет виду «закона стенки»

(38). Мы видим, что эксперимент дает существенное подтверждение логарифмического

распределения скорости.