Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

19.7 Random mixture of atoms 435

/RT

(µ

–

)/RT

0 1.0

−0.8

−0.5

0 1.0

(a) (b)

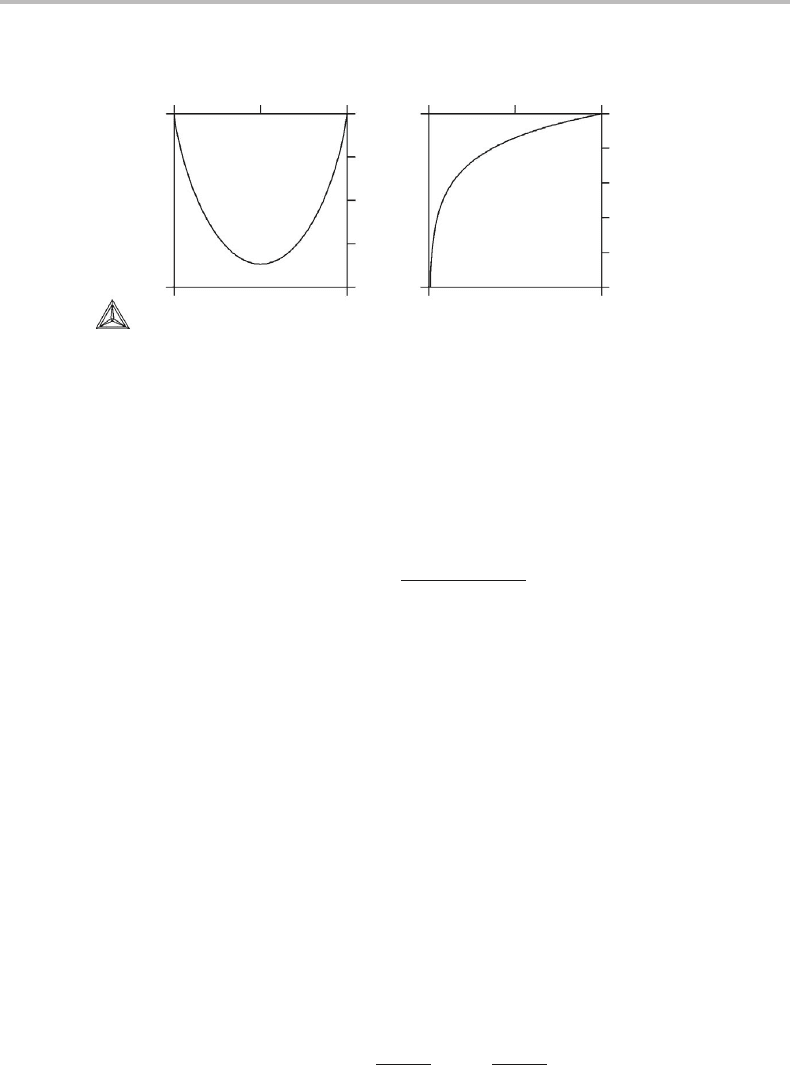
Figure 19.7 (a) Gibbs energy of mixing for an ideal, binary solution. (b) Variation of a chemical

potential in the same solution. In both cases the values have been normalized by dividing

with RT.

Let us consider a substance where all the sites are equivalent. Since all the various

atoms dissolved in the substance can substitute for each other, such a substance is called

a substitutional solution. The number of different ways in which N

atoms of A, N

atoms of B, N

atoms of C, etc., can be arranged is

W =

N !

! ...

. (19.40)

This randomness will give the following contribution to the entropy of the system accord-

ing to Boltzmann’s relation,

S/k = ln W = ln N! −  ln N

∼

N ln N −  N

ln N

=−N (N

/N) ln(N

/N) =−N x

ln x

(19.41)

since N is equal to  N

and x

= N

/N.

We may construct a model for an ideal substitutional solution by requiring that there

is no energy change on mixing the atoms. The only effect on the Gibbs energy would

come from the conﬁgurational disorder,

G =−T S = NkTx

ln x

, (19.42)

where N is the number of moles of atoms. Let us consider an ideal system with one mole

of atoms. Using Eq. (4.6)weobtain

G

=−T S = N

kTx

ln x

= RTx

ln x

(19.43)

µ

= G

∂G

∂x

− x

∂G

∂x

= RT ln x

. (19.44)

Figure 19.7 gives G

and µ

for an ideal, binary A–B system. It is worth emphasizing

that µ

goes to −∞as x

goes to 0. As a consequence the G

curve should be vertical

at its end-points. However, this tendency starts to develop so close to the end-points that

it is hardly discernible.

436 Modelling of disorder

In the model for an ideal solution there is no internal variable because the situation

has been completely ﬁxed by the assumption of random mixing. The situation will be

different if all the arrangements do not have the same energy. The disorder will then be

incomplete and one can introduce internal variables describing short- and long-range

order. This phenomenon will be described in Section 22.6.However, there is a class of

solution phases where all the sites are not equivalent and they may be, at the same time,

close to random in one sense and well ordered in another. They will be discussed in the

next sections.

Exercise 19.6

An A–B–C alloy is prepared by mixing x

moles of pure C with 1 – x

moles of an

A–B alloy. Calculate (a) the entropy of mixing in 1 – x

moles of the initial A–B alloy,

(b) the entropy due to the mixing of C into the A–B alloy and (c) the sum of the two

contributions.

Hint

The A content of the initial alloy can be expressed as x

/(x

+ x

)ifx

and x

refer to

the ﬁnal, ternary alloy. The effect of mixing C with a mixture of A + Bisthe same as the

effect of mixing C with a single element which could very well consist of two isotopes.

Remember that x

+ x

= 1 − x

Solution

S(a) = (1 − x

) ·{x

/(x

+ x

) · ln[x

/(x

+ x

)] + x

/(x

+ x

) · ln[x

/(x

)]}=x

ln x

+ x

ln x

− (x

+ x

) ln(x

+ x

); S(b) = x

ln x

+ (1 − x

)

ln(1 − x

) = x

ln x

+ (x

+ x

) ln(x

+ x

); S(c) = x

ln x

+ x

ln x

19.8 Restricted random mixture

Many crystalline phases have more than one family of sites. It is convenient to describe

such phases with the use of sublattices and the state may be deﬁned by giving the site

fractions (see Section 4.8).

= N

. (19.45)

If the atoms in one sublattice are mixed with each other at random, they give the following

contribution to the entropy

S

=−kN



=−R



ln y

. (19.46)

19.9 Crystals with stoichiometric vacancies 437

Since entropy is an extensive property which obeys the law of additivity, one could add

the contributions from the individual sublattices,

S

= S

=−R



ln y

. (19.47)

This expression holds for one mole of atoms if there are no vacant sites. a

is then deﬁned

as N

/N, the fraction of all sites belonging to the s sublattice, and a

is unity. One

may instead like to consider one mole of formula units where the formula is written with

integers for all a

. Then a

is the number of atoms per formula unit.

This may be regarded as an ideal solution model for the particular type of crystalline

structure. If all the elements can go into all the sublattices with the same probability, this

model reduces to the previous ideal solution model because y

is then identical to x

Exercise 19.7

Consider a so-called Laves phase with two components each on two sublattices, (A, B)

(C, D)

. Calculate the entropy of mixing assuming random mixing within each sublattice

for equal amounts of A and B and also for C and D. Compare with the ideal entropy of

mixing when all four components are mixed randomly with each other.

Hint

Consider 3 moles of atoms, 0.5 of A, 0.5 of B, 1 of C and 1 of D.

Solution

S/R =−1 · (0.5ln0.5 + 0.5ln0.5) − 2 · (0.5ln0.5 + 0.5ln0.5) =+3ln2 = 2.08.

Foranideal solution we get

S/R = 3[(1/6) ln(1/6) + (1/6) ln(1/6) + (2/6) ln(2/6) +(2/6) ln(2/6)] = 3.99.

19.9 Crystals with stoichiometric vacancies

A binary crystal can vary in composition even if each component is restricted to its own

sublattice. An example is w¨ustite which has separate sublattices for Fe and O. The Fe

sublattice can have vacant sites and we should thus write the formula as (Fe,Va)

.We

shall call such vacancies stoichiometric vacancies because in the simplest case, their

number is ﬁxed by the stoichiometric imbalance between the amounts of the elements.

The entropy of disorder in a crystal with any kind of vacancies is given by the expression

already discussed, if the vacancies are distributed at random on a sublattice. The vacancies

are then treated as the atoms of any element and one must deﬁne their site fraction, y

On the other hand, the vacancies are not included in the mole fractions x

which give

438 Modelling of disorder

the composition of the crystal. Consequently, when evaluating x from y, one should not

include the vacancies in the summation. We can give the equation as







−





. (19.48)

On the other hand, it is not always possible to calculate the y values from the overall

composition given by the set of x values. If each element is dissolved in one sublattice

only, then we can still evaluate the site fractions from the composition of the crystal

provided that there is at least one sublattice without vacancies. First we can identify that

sublattice as the one having the largest value of x

. Let us denote that sublattice by

r. The site fractions in any sublattice t are then given by

= x



. (19.49)

If y

in any sublattice is less than unity then the difference from unity gives the site

fraction of vacancies

= 1 −



. (19.50)

This relation illustrates why they are called stoichiometric vacancies. The amount of

stoichiometric vacancies does not change directly with the temperature but there may

be an indirect effect if the phase is in equilibrium with another phase. The composition

may then vary by an exchange of atoms between the phases. The amount of vacancies

can also vary if the composition of the other phase varies by an action from the outside.

A typical example is an oxide in equilibrium with an atmosphere of variable P

Exercise 19.8

We know the composition of an oxide by chemical analysis as x

= 0.252, x

= 0.094

and x

= 0.654. Calculate the site fractions under the assumption that the oxide is a

so-called stoichiometric phase with only a small deviation from stoichiometry.

Hint

Suppose that U and Pu occupy one sublattice and O another. The number of sites can

then be estimated from the number of atoms supposing there are no vacancies. Vacancies

can then be assumed on one sublattice for stoichiometric reasons.

Solution

+ x

= 0.346; x

/(x

+ x

) = 0.654/0.346 = 1.89. This is close to 2. We may

thus assume that the formula is (U,Pu)

(O,Va)

and we ﬁnd y

= 0.654 · 1/2 · 0.346 =

0.945; y

= 0.055.

19.10 Interstitial solutions 439

19.10 Interstitial solutions

Phases with two or more sublattices are often called compounds or intermediary phases,

or intermetallic phases when appropriate. Such compounds may be strictly stoichiometric

or may show a deviation from stoichiometry, caused by defects. One such defect is the

vacancy. A related case is the interstitial solution where some solute atoms dissolve in

acrystalline solvent by going into interstitial sites that are initially empty. These sites

form a sublattice. An example is the solution of carbon in the bcc modiﬁcation of iron,

so-called ferrite or α-Fe. The formula can be written as Fe

(Va,C)

. The entropy of

interstitial solutions can be treated with the method discussed in the preceding sections.

A more complicated case occurs when an element goes mainly into ordinary lattice sites

but some of its atoms go into interstitial sites.

In Section 4.8 we found that it was possible to derive an expression for the chemical

potential of a compound in a stoichiometric phase but not for the chemical potential of an

element. The situation is different for a phase with vacancies. For the interstitial solution

of C in α–Fe we can by standard methods derive expressions for µ

FeC

and µ

FeVa

.We

can thus evaluate µ

from

(µ

FeC

− µ

) =

+ µ

−

− µ

= µ

− µ

= µ

. (19.51)

because we can usually assume that the chemical potential of vacancies is zero. Assuming

random mixing of carbon atoms and vacancies we obtain the following contributions to

the entropy of mixing, the Gibbs energy of mixing and the chemical potential of carbon

S

=−3R(y

ln y

+ y

ln y

) (19.52)

G

= 3RT(y

ln y

+ y

ln y

) (19.53)

µ

= µ

− µ



G

∂G

∂y

−



∂G

∂y

− G

−

∂G

∂y



∂G

∂y





∂G

∂y

−

∂G

∂y



· 3RT ln

= RT ln

1 − y

. (19.54)

Interstitial solutions will be further discussed in Section 21.2.

It is important to notice that the deviation from stoichiometry of a compound may also

be caused by some atoms going into sites of the ‘wrong’ sublattice (in that connection

called anti-sites) or into interstitial sites.

Exercise 19.9

The interstitial solution of carbon in fcc- and bcc-iron can be represented with the formula

(Fe)

(Va,C)

and (Fe)

(Va,C)

, respectively. The martensitic transformation from fcc to

bcc is very rapid and carbon is not able to take advantage of the additional interstitial

sites. Estimate how much larger the driving force for the martensitic transformation

440 Modelling of disorder

would have been if carbon could be distributed among all the sites available in bcc-Fe.

Make a numerical calculation for an Fe-C alloy with a molar content of 0.02 C.

Hint

For simplicity, suppose that the redistribution of carbon atoms has an effect on the Gibbs

energy through the ideal entropy term only. Consider a system with one mole of Fe atoms

and thus z

= 0.02/0.98 = 0.0204 moles of C atoms.

Solution

G = 3RT[(z

/3) ln(z

/3) + (1 − z

/3) ln(1 − z

/3)] − RT[z

ln z

+ (1 − z

)

ln(1 − z

)] = RT(−0.1219 + 0.0996) =−0.223RT. The driving force would inc-

rease with 0.223RT.

Mathematical modelling of

solution phases

20.1 Ideal solution

The thermodynamic properties of some solutions were illustrated graphically in

Section 7.1 and some mathematical expressions were also given. We shall now give

a more thorough discussion. In Section 18.7 we mentioned the possibility of modelling

a special physical effect, p, in a substance and deﬁning the remaining part of the Gibbs

energy as the property of a hypothetical state, h, which does not have that physical effect,

= G

+ G

. (20.1)

This approach can also be applied to solution phases. The most important application

is the treatment of the thermodynamic effects of mixing the atoms in a solution. The

hypothetical state would then be a so-called mechanical mixture of the pure components

at the same temperature and pressure,

= x

. (20.2)

The physical effect, G

would here be the contribution due to the intimate mixing of the

atoms in a solution. It is usually denoted by

,which is thus deﬁned by

= x

. (20.3)

The mechanical mixture may be regarded as a reference for the properties of a solution

and

gives the solution behaviour. It is called Gibbs energy of mixing but a better

name would have been ‘Gibbs energy of solution’ because it represents the effect of

forming a solution from a mechanical mixture. For a binary system the reference is a

straight line in the molar Gibbs energy diagram, in a ternary system it is a plane, etc.

Earlier, in Fig. 7.1,itwas demonstrated that one can use this straight line in a binary

system as the line of reference in a molar Gibbs energy diagram and the concept of Gibbs

energy of mixing was introduced.

The simplest model for the intimate mixing of atoms in a solution is based on the

assumption of random mixing and no particular interactions between atoms of different

kinds. For that case we have

= x

− T ·

ideal

, (20.4)

442 Mathematical modelling of solution phases

(a) (b)

Figure 20.1 Characteristic shapes of the molar Gibbs energy curves in (a) binary and (b) ternary

systems, caused by the entropy of mixing.

and expressions for the ideal entropy of mixing in phases with different structures were

derived in Sections 19.7 to 19.10.Asolution obeying such an equation may be called an

ideal solution. For an ideal substitutional solution we have

ideal

=−Rx

ln x

(20.5)

= x

+ RTx

ln x

, (20.6)

and we may also deﬁne a partial ideal entropy of mixing for component I,

ideal

=−R ln x

(20.7)

Sometimes one explicitly requires that the molar volume of an ideal solution should be

equal to a weighted average of the values for the pure components. It is easy to see that

Eq. (20.4) satisﬁes this requirement because the derivative with respect to P yields

= ∂G

/∂ P = x

∂

/∂ P = x

. (20.8)

The term −T ·

ideal

is important even in real, non-ideal solutions and it gives the Gibbs

energy its characteristic shape of a hanging rope for a binary system and a canopy for a

ternary. This has already been illustrated in a number of diagrams in Sections 7.1 and

7.10 and is again shown in Fig. 20.1.

Exercise 20.1

Suppose one knows that a binary solution is not ideal because the molar volume obeys

the relation: V

= x

+ x

·|

−

|. Examine the effect on G

−

= 2 · 10

−6

mol.

Hint

Represent G

with x

+ x

− T ·

ideal

+ x

L and evaluate the effect

on L.

20.2 Mixing quantities 443

Solution

Compare with V

= ∂G

∂ P = x

+ x

∂ L/∂ P. Thus, ∂ L/∂ P =

(

−

) and, neglecting the pressure dependence of

−

,weﬁndL = L

P ·



(

−

). At 1 bar (10

Pa) this effect would increase L by 10

· 2 ·10

−6

0.2Jmol. This is negligible in most cases.

20.2 Mixing quantities

It is convenient to compare the value of any molar quantity in a solution with the weighted

average of the values for the pure components and deﬁne a molar quantity of mixing,

= x

. (20.9)

The additional requirement for an ideal solution, mentioned in the preceding sec-

tion, may thus be formulated by stating that the volume of mixing,

, must be

zero.

Partial quantities of mixing can be deﬁned relative to the value for the pure

component,

= A

−

. (20.10)

It is evident that all relations derived for A

and A

in Section 4.2 also apply to

and

because the references

will drop out from all such relations. We get, for

instance,

= A

− x

= x

− x

= x

−

) = x

. (20.11)

We ﬁnd, as for A

in Section 4.1,

∂

∂x

−



∂

∂x

. (20.12)

Exercise 20.2

Show that the partial enthalpy of mixing can be calculated from

= ∂(

/T )/

∂(1/T ).

Hint

We know H

= ∂(G

/T )/∂(1/T ). Use

= H

−

and

= G

−

Solution

∂(

/T )∂(1/T ) = ∂(G

/T )/∂(1/T ) − ∂(

/T )/∂(1/T ) = H

−

444 Mathematical modelling of solution phases

20.3 Excess quantities

The various mixing quantities were deﬁned relative to the mechanical mixture of the

components. In the same way one may deﬁne excess quantities relative to an ideal

solution, e.g.



− T ·

ideal

. (20.13)

The excess quantities represent the deviation from ideal behaviour and are thus subject

to direct study and modelling. In this chapter we shall examine mathematical models

of the excess Gibbs energy and in the next chapter we shall discuss some very simple

physical models.

From the excess Gibbs energy one may deﬁne partial excess Gibbs energies and obtain,

by standard procedures,

+ ∂

/∂x

− x

∂

/∂x

(20.14)

= G

−

+ T ·

ideal

(20.15)

= x

(20.16)

= S

−

ideal

(20.17)

= H

−

. (20.18)

We note that it is not necessary to introduce the concept of excess enthalpy because

all enthalpy of mixing is in excess of the ideal solution behaviour. For a substitutional

solution we get

= G

−

− RT ln x

. (20.19)

= S

−

− R ln x

(20.20)

Exercise 20.3

Using a Maxwell relation at constant T and P we get ∂ G

/∂ N

= ∂

G/∂ N

∂ N

∂

G/∂ N

∂ N

= ∂G/∂ N

. Using this relation, show that ∂

/∂ N

= ∂

/∂ N

Hint

+ RT ln x

; ∂ x

/∂ N

=−x

/N; ∂x

/∂ N

=−x

/N.

Solution

∂G

/∂ N

=RT(1/x

)·(−x

/N) + ∂

/∂ N

=−RT/N +∂

/∂ N

; ∂G

/∂ N

−RT/N + ∂

/∂ N

.Ifthe two left-hand sides are equal, we obtain ∂

/∂ N

∂

/∂ N