Hibbeler R.C. Structural Analysis

Подождите немного. Документ загружается.

610 CHAPTER 16 PLANE FRAME ANALYSIS U SING THE STIFFNESS METHOD

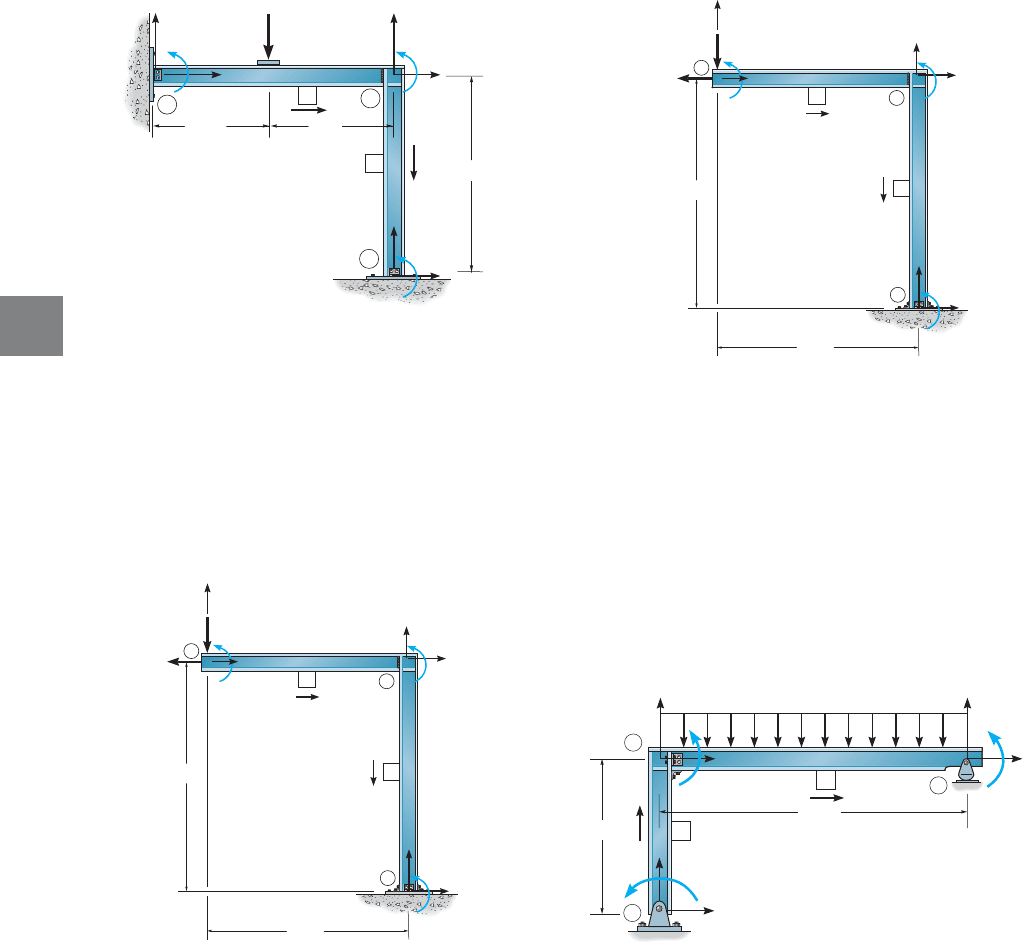
16–9. Determine the stiffness matrix K for the frame.Take

, , for each member.

16–10. Determine the support reactions at

① and ➂. Take

, for each member.A = 10 in

I = 300 in

E = 29110

2 ksi,

A = 10 in

I = 300 in

E = 29110

2 ksi

10 ft

20 ft

2 k/ft

Probs. 16–9/16–10

16–7. Determine the structure stiffness matrix K for

the frame. Take , ,

for each member.

A = 20 in

I = 650 in

E = 29110

2 ksi

Prob. 16–7

6 k

4 k

12 ft

10 ft

*16–8. Determine the components of displacement at ①.

Take , , for each

member.

A = 20 in

I = 650 in

E = 29110

2 ksi

Prob. 16–8

6 k

4 k

12 ft

10 ft

Prob. 16–6

4 m

2 m

60 kN

16–6. Determine the support reactions at pins ① and ➂.

Take , ,

for each member.

A = 15110

2 mm

I = 350110

2 mm

E = 200 GPa

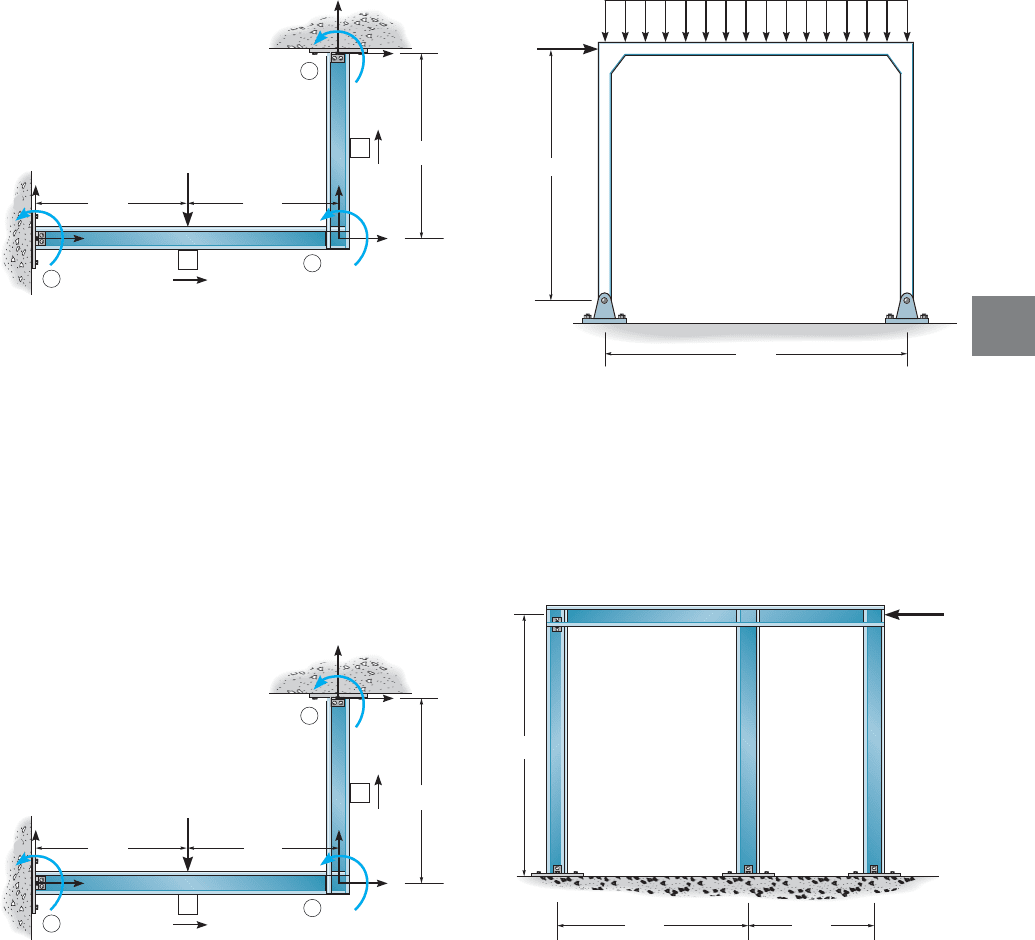
16.4 A

PPLICATION OF THE STIFFNESS METHOD FOR FRAME ANALYSIS 611

16–13. Use a computer program to determine the reactions

on the frame. AE and EI are constant.

16–11. Determine the structure stiffness matrix K for the

frame. Take , , for

each member.

A = 20 in

I = 700 in

E = 29110

2 ksi

16–14. Use a computer program to determine the reactions

on the frame. Assume A, B, D, and F are pins. AE and EI

are constant.

16 ft

20 k

12 ft12 ft

6 m

4 m

8 m

8 kN

15 k

20 ft

24 ft

1.5 k/ft

Prob. 16–11

*16–12. Determine the support reactions at the pins

①

and ➂. Take , , for

each member.

A = 20 in

I = 700 in

E = 29110

2 ksi

16 ft

20 k

12 ft12 ft

Prob. 16–12

Prob. 16–13

Prob. 16–14

612

Matrix Algebra for

Structural Analysis

APPENDIX

A.1 Basic Definitions and Types

of Matrices

With the accessibility of desk top computers, application of matrix algebra

for the analysis of structures has become widespread. Matrix algebra

provides an appropriate tool for this analysis, since it is relatively easy to

formulate the solution in a concise form and then perform the actual

matrix manipulations using a computer. For this reason it is important

that the structural engineer be familiar with the fundamental operations

of this type of mathematics.

Matrix. A matrix is a rectangular arrangement of numbers having m

rows and n columns.The numbers, which are called elements, are assembled

within brackets. For example, the A matrix is written as:

Such a matrix is said to have an order of (m by n). Notice that the

first subscript for an element denotes its row position and the second

subscript denotes its column position. In general, then, is the element

located in the ith row and jth column.

Row Matrix. If the matrix consists only of elements in a single row,

it is called a row matrix. For example, a row matrix is written as

Here only a single subscript is used to denote an element, since the row

subscript is always understood to be equal to 1, that is,

and so on.

= a

A = [a

]

1 * n

m * n

A = D

Column Matrix. A matrix with elements stacked in a single column

is called a column matrix. The column matrix is

Here the subscript notation symbolizes and so on.

Square Matrix. When the number of rows in a matrix equals the

number of columns, the matrix is referred to as a square matrix. An

square matrix would be

Diagonal Matrix. When all the elements of a square matrix are

zero except along the main diagonal, running down from left to right, the

matrix is called a diagonal matrix. For example,

Unit or Identity Matrix. The unit or identity matrix is a diagonal

matrix with all the diagonal elements equal to unity. For example,

Symmetric Matrix. A square matrix is symmetric provided

For example,

A = C

352

5 -14

248

= a

I = C

100

010

001

A = C

0 a

00a

A = D

n * n

= a

A = D

m * 1

A.1 BASIC DEFINITIONS AND TYPES OF MATRICES 613

614 APPENDIX AMATRIX ALGEBRA FOR S TRUCTURAL A NALYSIS

A.2 Matrix Operations

Equality of Matrices. Matrices A and B are said to be equal if

they are of the same order and each of their corresponding elements are

equal, that is, For example, if

then

Addition and Subtraction of Matrices. Two matrices can be

added together or subtracted from one another if they are of the same

order. The result is obtained by adding or subtracting the corresponding

elements. For example, if

then

Multiplication by a Scalar. When a matrix is multiplied by a

scalar, each element of the matrix is multiplied by the scalar. For

example, if

then

Matrix Multiplication. Two matrices A and B can be multiplied

together only if they are conformable. This condition is satisfied if the

number of columns in A equals the number of rows in B. For example, if

(A–1)

then AB can be determined since A has two columns and B has two rows.

Notice, however, that BA is not possible.Why?

A = c

B = c

kA = c

-24 -6

-36 12

A = c

6 -2

k =-6

A + B = c

115

A - B = c

11 -1

1 -5

A = c

2 -1

B = c

-58

A = B.

A = c

4 -3

B = c

4 -3

= b

A.2 MATRIX OPERATIONS 615

If matrix A having an order of is multiplied by matrix B

having an order of it will yield a matrix C having an order of

that is,

The elements of matrix C are found using the elements of A and

of B as follows:

(A–2)

The methodology of this formula can be explained by a few simple

examples. Consider

By inspection, the product is possible since the matrices are

conformable, that is, A has three columns and B has three rows. By

Eq. A–2, the multiplication will yield matrix C having two rows and one

column. The results are obtained as follows:

Multiply the elements in the first row of A by corresponding elements

in the column of B and add the results; that is,

Multiply the elements in the second row of A by corresponding

elements in the column of B and add the results; that is,

Thus

C = c

= c

=-1122+ 6162+ 1172= 41

= c

= 2122+ 4162+ 3172= 49

C = AB

A = c

243

-161

d B = C

k = 1

1m * n21n * q21m * q2

AB = C

1m * q2,

1n * q2

1m * n2

616 APPENDIX AMATRIX ALGEBRA FOR S TRUCTURAL A NALYSIS

As a second example, consider

Here again the product can be found since A has two columns

and B has two rows. The resulting matrix C will have three rows and two

columns. The elements are obtained as follows:

The scheme for multiplication follows application of Eq. A–2. Thus,

Notice also that BA does not exist, since written in this manner the

matrices are nonconformable.

The following rules apply to matrix multiplication.

1. In general the product of two matrices is not commutative:

(A–3)

2. The distributive law is valid:

(A–4)

3. The associative law is valid:

(A–5)

Transposed Matrix. A matrix may be transposed by interchanging

its rows and columns. For example, if

A = C

B = [b

]

A1BC2= 1AB2C

A1B + C2= AB + AC

AB Z BA

C = C

147

532

-28 18

=-2172+ 8142= 18

1third row of A times second column of B2

=-2122+ 81-32=-28

1third row of A times first column of B2

= 4172+ 1142= 32

1second row of A times second column of B2

= 4122+ 11-32= 5

1second row of A times first column of B2

= 5172+ 3142= 47

1first row of A times second column of B2

= 5122+ 31-32= 1

1first row of A times first column of B2

C = AB

A = C

-28

B = c

-34

A.2 MATRIX OPERATIONS 617

Then

Notice that AB is nonconformable and so the product does not exist.

(A has three columns and B has one row.) Alternatively, multiplication

is possible since here the matrices are conformable (A has three

columns and has three rows). The following properties for transposed

matrices hold:

(A–6)

(A–7)

(A–8)

This last identity will be illustrated by example. If

Then, by Eq. A–8,

Matrix Partitioning. A matrix can be subdivided into submatrices

by partitioning. For example,

Here the submatrices are

= c

d A

= c

= [a

] A

= [a

]

A = C

S= c

28 -2

28 -12

d = c

28 -2

28 -12

28 28

-2 -12

= c

28 -2

28 -12

1 -3

= c

2 -3

A = c

1 -3

d B = c

1AB2

= B

1kA2

= kA

1A + B2

= A

+ B

= C

S B

= C

618 APPENDIX AMATRIX ALGEBRA FOR S TRUCTURAL A NALYSIS

The rules of matrix algebra apply to partitioned matrices provided the

partitioning is conformable. For example, corresponding submatrices of A

and B can be added or subtracted provided they have an equal number of

rows and columns. Likewise, matrix multiplication is possible provided

the respective number of columns and rows of both A and B and their

submatrices are equal. For instance, if

then the product AB exists, since the number of columns of A equals the

number of rows of B (three). Likewise, the partitioned matrices are

conformable for multiplication since A is partitioned into two columns

and B is partitioned into two rows, that is,

Multiplication of the submatrices yields

A.3 Determinants

In the next section we will discuss how to invert a matrix. Since this

operation requires an evaluation of the determinant of the matrix, we will

now discuss some of the basic properties of determinants.

A determinant is a square array of numbers enclosed within vertical

bars. For example, an nth-order determinant, having n rows and n

columns, is

(A–9)

AB = D

-4

d + c

-7

-35

-4

-20

[12 18] + [56 32]

T= C

-39 -18

68 50

= [8][7 4] = [56 32]

= [6 3]c

2 -1

d = [12 18]

= c

-1

-5

d[7 4] = cc

-7 -4

-35 -20

= c

-20

2 -1

d = c

-42

AB = c

d = c

+ A

A = C

41-1

-20-5

63 8

S B = C

2 -1

A.3 DETERMINANTS 619

Evaluation of this determinant leads to a single numerical value which

can be determined using Laplace’s expansion. This method makes use of

the determinant’s minors and cofactors. Specifically, each element of a

determinant of nth order has a minor which is a determinant of order

This determinant (minor) remains when the ith row and jth column

in which the element is contained is canceled out. If the minor is

multiplied by it is called the cofactor of and is denoted as

(A–10)

For example, consider the third-order determinant

The cofactors for the elements in the first row are

Laplace’s expansion for a determinant of order n, Eq. A–9, states that

the numerical value represented by the determinant is equal to the sum

of the products of the elements of any row or column and their respective

cofactors, i.e.,

or (A–11)

For application, it is seen that due to the cofactors the number D is defined

in terms of n determinants (cofactors) of order each. These

determinants can each be reevaluated using the same formula, whereby

one must then evaluate determinants of order and so

on.The process of evaluation continues until the remaining determinants

to be evaluated reduce to the second order, whereby the cofactors of the

elements are single elements of D. Consider, for example, the following

second-order determinant

We can evaluate D along the top row of elements, which yields

Or, for example, using the second column of elements, we have

D = 51-12

1 + 2

1-12+ 21-12

2 + 2

132= 11

D = 31-12

1 + 1

122+ 51-12

1 + 2

1-12= 11

D =

-12

1n - 22,1n - 12

n - 1

D = a

+ a

1j = 1, 2, Á , or n2

D = a

+ a

1i = 1, 2, Á , or n2

= 1-12

1 + 3

= 1-12

1 + 2

= 1-12

1 + 1

= 1-12

i + j

1-12

i + j

n - 1.