Hibbeler R.C. Structural Analysis
Подождите немного. Документ загружается.


290 CHAPTER 7APPROXIMATE ANALYSIS OF S TATICALLY INDETERMINATE STRUCTURES
7
EXAMPLE 7.7
C
4 m
30 kN
15 kN
4 m
B
A
G
H
I
J
D
K
E
L
F
6 m
(a)
30 kN
2 m
H
x
H
y
K
y
K
x
3 m 3 m
(
c
)
Fig. 7–16
6 m
(b)
–
x 3 m
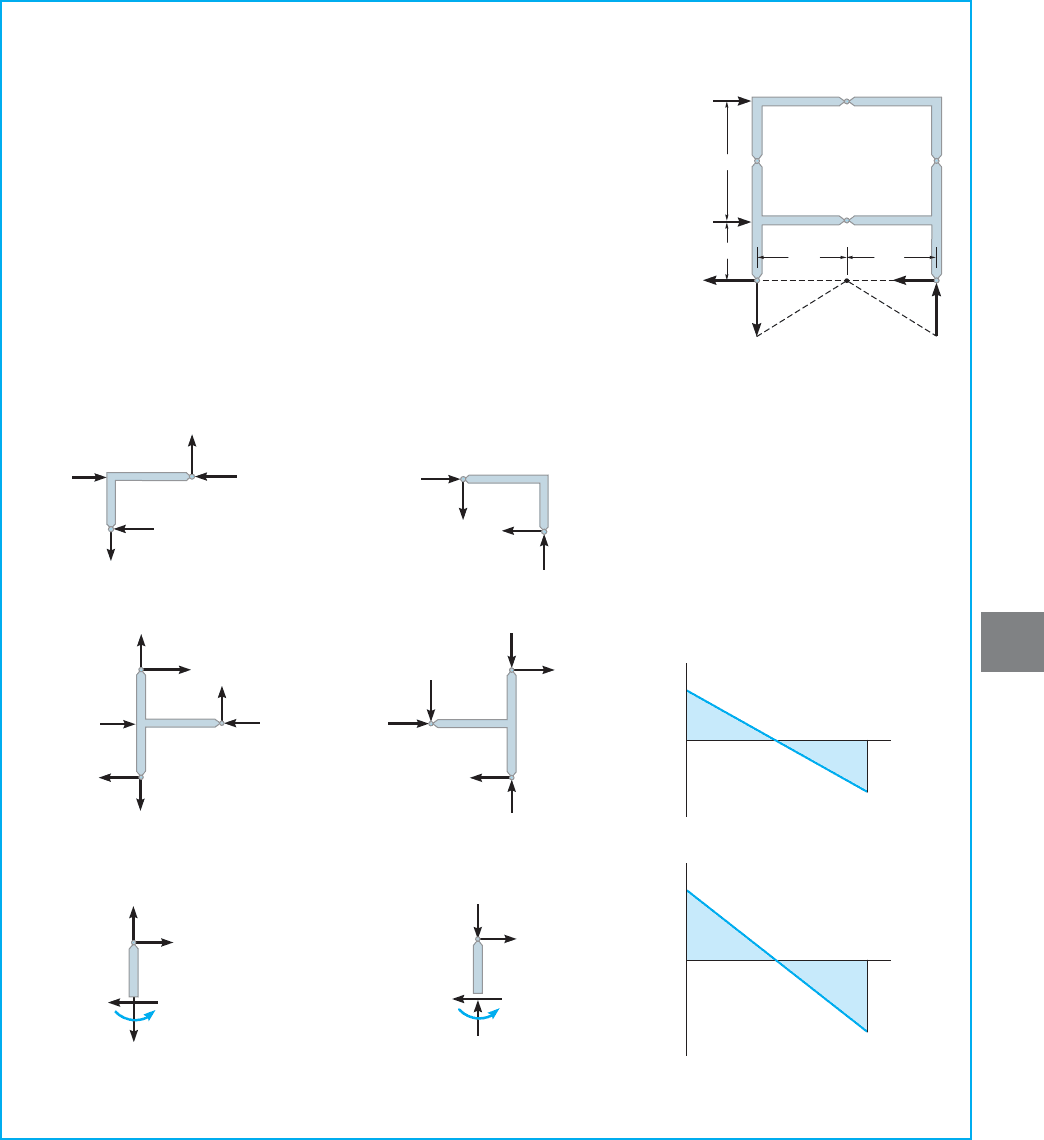
Determine (approximately) the reactions at the base of the columns
of the frame shown in Fig. 7–16a. The columns are assumed to have
equal cross-sectional areas. Use the cantilever method of analysis.
SOLUTION
First hinges are placed at the midpoints of the columns and girders.
The locations of these points are indicated by the letters G through L
in Fig. 7–16a.The centroid of the columns’ cross-sectional areas can be
determined by inspection, Fig. 7–16b, or analytically as follows:
The axial stress in each column is thus proportional to its distance
from this point. Here the columns have the same cross-sectional area,
and so the force in each column is also proportional to its distance
from the centroid. Hence, a section through the hinges H and K at the
top story yields the free-body diagram shown in Fig. 7–16c. Note how
the column to the left of the centroid must be subjected to tension
and the one on the right is subjected to compression. This is necessary
in order to counteract the tipping caused by the 30-kN force.
Summing moments about the neutral axis, we have
The unknowns can be related by proportional triangles, Fig. 7–16c,
that is,
Thus,
H
y
= K
y
= 10 kN
H
y
3
=
K
y
3
or
H
y
= K
y
-30122+ 3H
y
+ 3K
y
= 0d+©M
= 0;
x =
©x
'
A
©A
=
01A2+ 61A2
A + A
= 3 m
7.6 LATERAL LOADS ON BUILDING FRAMES: CANTILEVER METHOD 291
7
In a similar manner, using a section of the frame through the hinges
at G and L, Fig. 7–16d, we have
Since or then
Each part of the frame can now be analyzed using the above results.
As in Examples 7–5 and 7–6, we begin at the upper corner where the
applied loading occurs, i.e., segment HCI, Fig. 7–16a. Applying the
three equations of equilibrium, yields
the results for and respectively, shown on the free-body
diagram in Fig. 7–16e. Using these results, segment IDK is analyzed
next, Fig. 7–16f; followed by HJG, Fig. 7–16g; then KJL, Fig. 7–16h; and
finally the bottom portions of the columns, Fig. 7–16i and Fig. 7–16j.
The moment diagrams for each girder are shown in Fig. 7–16k.
I
y
,I
x
,H
x
,
©F
y
= 0,©F
x
= 0,©M
I
= 0,
G
y
= L
y
= 35 kN
G
y
= L
y
,G
y
>3 = L
y
>3
-30162- 15122+ 3G
y
+ 3L
y
= 0d+©M
= 0;
15 kN
10 kN
15 kN
2 m
2 m
3 m
J
x
7.5 kN
J
y
25 kN
35 kN
G
x
22.5 kN
(g)
J
G
H
10 kN
15 kN
25 kN
3 m
7.5 kN
2 m
2 m
L
x
22.5 kN
35 kN
(
h
)
K
J
L
2 m
35 kN
22.5 kN
A
x
22.5 kN
M
A
45 kNm
A
y
35 kN
(i)
G
A
30 kN
2 m
3 m
H
x
15 kN
10 kN
I
x
15 kN
I
y
10 kN
I
(
e
)
C
H
15 kN
10 kN
3 m
2 m
K
x
15 kN
10 kN
(
f
)
D
I
K
2 m
35 kN
22.5 kN
F
x
22.5 kN
M
F
45 kNm
F
y
35 kN
(j)
L
F
30
30
M (kNm)
3
6
3
6
x (m)
(k)
75
75
M (kNm)
x (m)
30 kN
4 m
G
x
G
y
L
y
L
x
3 m 3 m
(d)
15 kN
2 m
292 CHAPTER 7APPROXIMATE ANALYSIS OF S TATICALLY INDETERMINATE STRUCTURES
7
Fig. 7–17
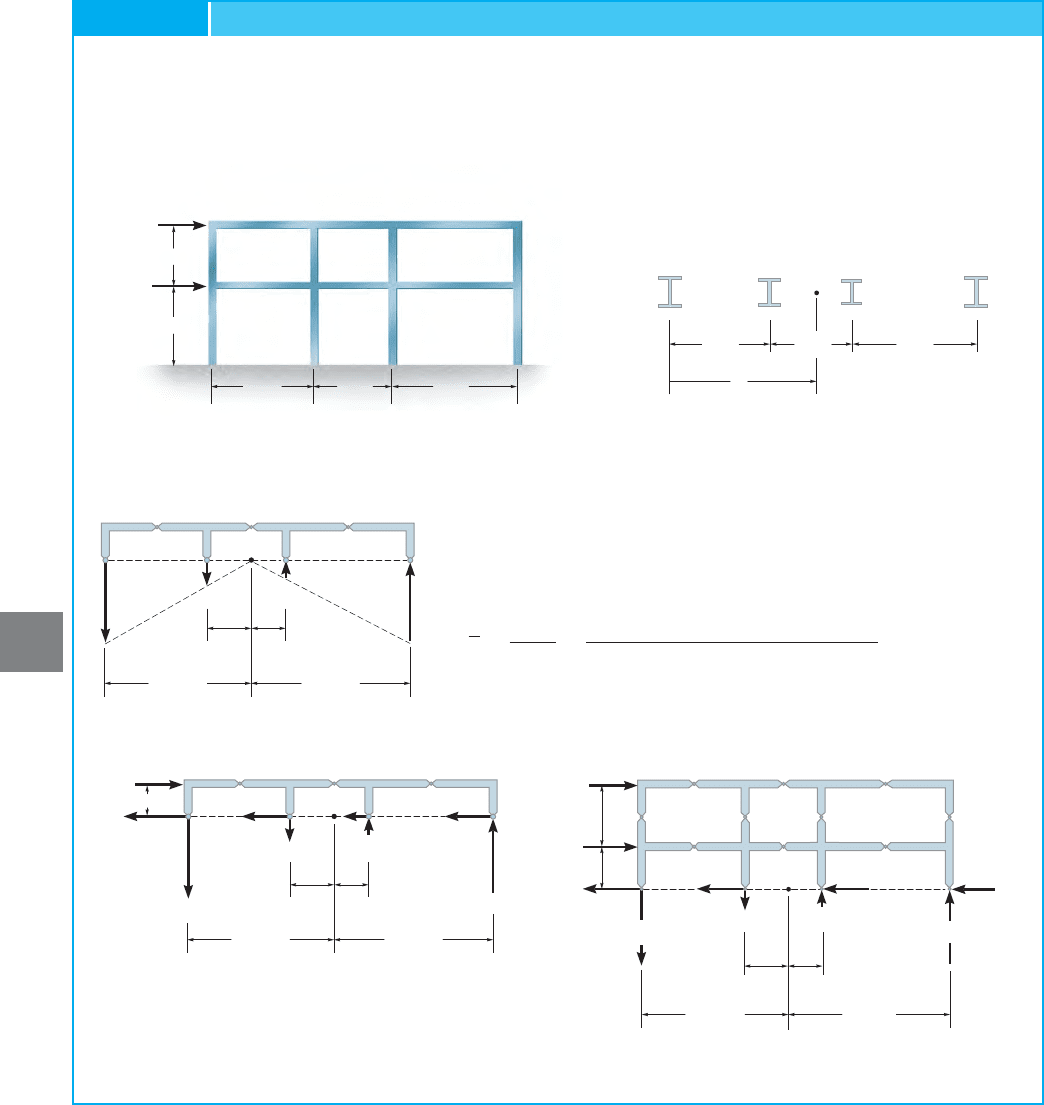
Show how to determine (approximately) the reactions at the base of the
columns of the frame shown in Fig. 7–17a. The columns have the cross-
sectional areas shown in Fig. 7–17b. Use the cantilever method of analysis.
EXAMPLE 7.8
SOLUTION
First, hinges are assumed to exist at the centers of the girders and
columns of the frame, Fig. 7–17d and Fig. 7–17e. The centroid of the
columns’ cross-sectional areas is determined from Fig. 7–17b as follows:
First we will consider the section through hinges at L, M, N and O.
x =
©x
'
A
©A
=
01102+ 20182+ 35162+ 601102
10 + 8 + 6 + 10
= 28.53 ft
8 k
10 k
12 ft
16 ft
L
E
PQ R
10 in
2
IJ
K
8 in
2
6 in
2
10 in
2
8 in
2
6 in
2
FG H
ONM 10 in
2
10 in
2
ABC D
20 ft 15 ft 25 ft
(a)
20 ft
(b)
15 ft 25 ft
10 in.
2
8 in.
2
6 in.
2
10 in.
2
–
x
S
N
S
O
28.53 ft 31.47 ft
(
c
)
8.53 ft 6.47 ft
S
L
S
M
8 k
6 ft
L
x
M
x
M
y
0.239 L
y
N
x
N
y
0.136 L
y
O
x
O
y
1.103 L
y
L
y
28.53 ft 31.47 ft
(d)
8.53 ft 6.47 ft
8 k
12 ft
10 k
E
x
F
x
G
x
H
x
E
y
3.627 k
F
y
0.868 k
G
y
0.494 k
H
y
4.001 k
8.53 ft 6.47 ft
28.53 ft 31.47 ft
(e)
8 ft

7.6 LATERAL LOADS ON BUILDING FRAMES: CANTILEVER METHOD 293
7
In this problem the columns have different cross-sectional areas, so we
must consider the axial stress in each column to be proportional to its
distance from the neutral axis, located at
We can relate the column stresses by proportional triangles, Fig. 7–17c.
Expressing the relations in terms of the force in each column, since
we have
Now that each force is related to L
y
, the free-body diagram is shown
in Fig. 7–17d.
Note how the columns to the left of the centroid are subjected to
tension and those on the right are subjected to compression. Why?
Summing moments about the neutral axis, we have
Solving,
Using this same method, show that one obtains the results in Fig. 7–17e
for the columns at E, F, G, and H.
We can now proceed to analyze each part of the frame. As in the
previous examples, we begin with the upper corner segment LP,
Fig. 7–17f. Using the calculated results, segment LEI is analyzed next,
Fig. 7–17g, followed by segment EA, Fig. 7–17h. One can continue to
analyze the other segments in sequence, i.e., PQM, then MJFI, then
FB, and so on.
L
y
= 0.725 k
M
y
= 0.174 k
N
y
= 0.0987 k
O
y
= 0.800 k
+ (0.136L
y
)16.47 ft2+ (1.103L
y
)131.47 ft2= 0
-8 k 16 ft2+ L
y
128.53 ft2+ (0.239L
y
)18.53 ft2d+©M
= 0;
O
y
10 in
2
=
31.47
28.53
a
L
y
10 in
2
b
O
y
= 1.103L
y
s
O
=
31.47 ft
28.53 ft
s
L
;
N
y
6 in
2
=
6.47
28.53
a
L
y
10 in
2
b
N
y
= 0.136L
y
s
N
=
6.47 ft
28.53 ft
s
L
;
M
y
8 in
2
=
8.53
28.53
a
L
y
10 in
2
b
M
y
= 0.239L
y
s
M
=
8.53 ft
28.53 ft
s
L
;
s = F/A,
x = 28.53 ft.
8 k
6 ft
10 ft
P
y
0.725 k
P
x
6.791 k
L
x
1.209 k
0.725 k
P
L
E
x
2.720 k
3.627 k
10 k
8 ft
6 ft
10 ft
1.209 k
0.725 k
I
x
8.489 k
I
y
2.902 k
L
I
E
3.627 k
8 ft
M
A
21.764 kft
2.720 k
A
y
3.627 k
A
x
2.720 k
E
A
(f)
(g)
(h)

294 CHAPTER 7APPROXIMATE ANALYSIS OF S TATICALLY INDETERMINATE STRUCTURES
7
6 m
AB C
EDF
8 m 8 m
15 kN
Prob. 7–35
15 ft
AB C ED
JI HGF
18 ft18 ft 18 ft 18 ft
4 k
Prob. 7–36
9 kN
5 m5 m 5 m
4 m
4 m
JK
L
GFEH
DCBA
I
12 kN
Probs. 7–37/7–38
12 ft
15 ft
4 k
5 k
A
D
E
F
C
B
12 ft
Probs. 7–39/7–40
7–35. Use the portal method of analysis and draw the
moment diagram for girder FED.
7–39. Use the portal method of analysis and draw the
moment diagram for column AFE.
*7–40. Solve Prob. 7–39 using the cantilever method of
analysis. All the columns have the same cross-sectional area.
PROBLEMS
7–37. Use the portal method and determine (approximately)
the reactions at supports A, B, C, and D.
7–38. Use the cantilever method and determine
(approximately) the reactions at supports A, B, C, and D.
All columns have the same cross-sectional area.
*7–36. Use the portal method of analysis and draw the
moment diagram for girder JIHGF.
7–41. Use the portal method and determine (approximately)
the reactions at A.
7–42. Use the cantilever method and determine
(approximately) the reactions at A. All of the columns have
the same cross-sectional area.
3 k
18 ft 20 ft
15 ft
15 ft
G
FE
H
D
CBA
I
4 k
Probs. 7–41/7–42

PROJECT PROBLEMS 295
7
7–43. Draw (approximately) the moment diagram for
girder PQRST and column BGLQ of the building frame.
Use the portal method.
*7–44. Draw (approximately) the moment diagram for
girder PQRST and column BGLQ of the building frame.
All columns have the same cross-sectional area. Use the
cantilever method.
7–45. Draw the moment diagram for girder IJKL of the
building frame. Use the portal method of analysis.
7–46. Solve Prob. 7–45 using the cantilever method of
analysis. Each column has the cross-sectional area indicated.
6 k
9 k
9 k
15 ft 15 ft 20 ft 20 ft
10 ft
10 ft
10 ft
PQR S T
KLM N O
FGH I J
ABC D E
Probs. 7–43/7–44
20 kN
24 (10
3
) m
2
Area
16 (10
3
) m
2
16 (10
3
) m
2
24 (10
3
) m
2
4 m 5 m 4 m
4 m
4 m
JKL
G
F
E
H
DCBA
I
40 kN
Probs. 7–45/7–46
15 ft
5 ft
4 ft 4 ft
wind
8 ft
3 ft
3 ft
3 ft
E
A
C
D
B
Prob. 7–1P
7–1P. The storage building bents shown in the photo are
spaced 10 ft apart and can be assumed pin connected at all
points of support. Use the idealized model shown and
determine the anticipated wind loading on the bent. Note
that the wind loading is transmitted from the wall to the
four purlins, then to the columns on the right side. Do an
approximate analysis and determine the maximum axial
load and maximum moment in column AB. Assume the
columns and knee braces are pinned at their ends.The building
is located on flat terrain in New Orleans, Louisiana, where
.V = 125 mi>h
PROJECT PROBLEMS

296 CHAPTER 7APPROXIMATE ANALYSIS OF S TATICALLY INDETERMINATE STRUCTURES
7
An approximate structural analysis is used to reduce a
statically indeterminate structure to one that is statically
determinate. By doing so a preliminary design of the
members can be made, and once complete, the more exact
indeterminate analysis can then be performed and the
design refined.
Trusses having cross-diagonal bracing within their panels
can be analyzed by assuming the tension diagonal supports
the panel shear and the compressive diagonal is a zero-force
member. This is reasonable if the members are long and
slender. For larger cross sections, it is reasonable to assume
each diagonal carries one-half the panel shear.
The approximate analysis of a vertical uniform load acting
on a girder of length L of a fixed-connected building frame
can be approximated by assuming that the girder does not
support an axial load, and there are inflection points
(hinges) located 0.1L from the supports.
a
b
P
2
P
1
R
1
R
2
F
2
F
1
R
1
F
b
F
a
V R
1
w
L
w
0.1L 0.1L
0.8L
CHAPTER REVIEW

CHAPTER REVIEW 297
7
Portal frames having fixed supports are approximately analyzed by assuming there are hinges at the midpoint of each
column height, measured to the bottom of the truss bracing. Also, for these, and pin-supported frames, each column is
assumed to support half the shear load on the frame.
For fixed-connected building frames subjected to lateral loads, we can assume there are hinges at the centers of the
columns and girders. If the frame has a low elevation, shear resistance is important and so we can use the portal method,
where the interior columns at any floor level carry twice the shear as that of the exterior columns. For tall slender frames,
the cantilever method can be used, where the axial stress in a column is proportional to its distance from the centroid of the
cross-sectional area of all the columns at a given floor level.
P
h
l
P
V
NN
V2V
Portal method
Cantilever method
P
P
h
—
2
P
—
2
P
—
2
assumed
hinges
P
inflection point

The deflection of this arch bridge must be carefully monitored while it
is under construction.

8
299
In this chapter we will show how to determine the elastic deflections of
a beam using the method of double integration and two important
geometrical methods, namely, the moment-area theorems and the
conjugate-beam method. Double integration is used to obtain equations
which define the slope and the elastic curve. The geometric methods
provide a way to obtain the slope and deflection at specific points
on the beam. Each of these methods has particular advantages or
disadvantages, which will be discussed when each method is presented.
8.1 Deflection Diagrams and the Elastic
Curve
Deflections of structures can occur from various sources, such as loads,
temperature, fabrication errors, or settlement. In design, deflections must
be limited in order to provide integrity and stability of roofs, and prevent
cracking of attached brittle materials such as concrete, plaster or glass.
Furthermore, a structure must not vibrate or deflect severely in order to
“appear” safe for its occupants. More important, though, deflections at
specified points in a structure must be determined if one is to analyze
statically indeterminate structures.
The deflections to be considered throughout this text apply only to
structures having linear elastic material response. Under this condition,
a structure subjected to a load will return to its original undeformed
position after the load is removed. The deflection of a structure is caused
Deflections
