Heubach S., Mansour T. Combinatorics of Compositions and Words

Подождите немного. Документ загружается.

Words 195

Deﬁnition 6.1 We denote the set of k-ary words of length n that contain the

pattern τ exactly r times by W

[k]

(τ; r), and the number of words in W

[k]

(τ; r)

by W

[k]

(n, r). The corresponding generating function is given by

[k]

(x, q)=



w∈W

[k]

occ

(w)



n,r≥0

[k]

(n, r)x

where occ

(w) denotes the number of occurrences of τ in the word w.Further-

more, we denote the set of k-ary words of length n that avoid the pattern τ by

[k]

(τ), and the number of words in AW

[k]

(τ) by AW

[k]

(n). The associated

generating functions are given by

[k]

(x)=



n≥0

[k]

(n)x

and (keeping track of the alphabet as well )

(x, y)=



k≥0

[k]

(x)y



n,k≥0

[k]

(n)x

If we consider several patterns at once, we replace τ by T and r by r in the

notation deﬁned above.

As mentioned before, pattern enumeration and pattern avoidance have been

studied ﬁrst for permutations, then for words, and ﬁnally for compositions,

generalizing the combinatorial object under consideration in each step. There-

fore words can be considered to be a special case of compositions. Speciﬁcally,

we can think of k-ary words of length n as compositions with n parts on the

set [k] where we disregard the order of the composition. Thus, we immedi-

ately can obtain results on pattern enumeration or avoidance in words from

the respective results for compositions by setting A =[k], x =1,andy = x

(whenever that is an allowed operation) to obtain that

[k]

(x, q)=C

[k]

(1,x,q)andAW

[k]

(x)=AC

[k]

(1,x).

In some instances, we cannot obtain the results for k-ary words from those

for compositions. One such example, where we cannot just substitute x =1

but have to do some additional work, is ﬁnding the generating function for

the number of words that avoid the pattern peak (see Example 4.27).

Many of the results presented in Chapters 4 and 5 have been obtained by

generalizing proofs for words, but not all results can be extended from words

to compositions. This is in part due to the fact that when we restrict the

set A =[k] under consideration, we can map the restricted set, no matter

whether it is A\{1}, A\{i} or A\{k}, to the alphabet [k −1], resulting in much

easier recurrence relations, with a much better chance of leading to explicit

results. A second factor that makes analysis of pattern avoidance in words

196 Combinatorics of Compositions and Words

simpler than that for compositions is that there are fewer classes of patterns

to consider. To make this statement more precise, we deﬁne Wilf-equivalence

for patterns in words.

Deﬁnition 6.2 Two subword patterns τ and ν are tight Wilf-equivalent if the

number of k-ary words of length n that avoid τ is the same as the number of

k-ary words of length n that avoid ν, for all n and k. Wedenotetwopatterns

that are tight Wilf-equivalent by τ

∼ ν.

Deﬁnition 6.3 Two nonsubword patterns τ and ν are called Wilf-equivalent

if the number of k-ary words of length n that avoid τ isthesameasthe

number of k-ary words of length n that avoid ν, for all n and k.Wedenote

two patterns that are Wilf-equivalent by τ ∼ ν.

Having deﬁned Wilf-equivalence, we can now discuss the symmetry classes

for patterns τ in words. Since we are no longer concerned with the sum of

the parts, a word and its complement are Wilf-equivalent, resulting in fewer

Wilf classes.

Deﬁnition 6.4 For any pattern τ,thesymmetry class of τ with respect to

enumeration or avoidance in words is given by {τ,R(τ),c(τ),R(c(τ))}.

It is easy to see that R(c(τ)) = c(R(τ)) for any type of pattern τ with

respect to pattern avoidance or enumeration in words. The fact that the com-

plement of a pattern is in the same symmetry class also explains the structural

phenomenon that we have seen in the results for enumeration or avoidance

of patterns in compositions. Oftentimes we had expressions for generating

functions that were very similar in structure, but nevertheless diﬀerent – now

we see why! The two patterns in question are complementary patterns, and

therefore the results have to agree once we set x = 1. This phenomenon can

be seen for example in Theorems 5.21 and 5.23.

We will revisit some of the results for compositions from the previous two

chapters and present the corresponding results for words in this section, to-

gether with the original references (if the results were already known for

words).

6.3 Subword patterns

We start by looking at the simplest subword patterns, namely 11 and 12.

Example 6.5 Since 11 and 12 can be thought of as level and rise, we can

exploit Theorem 4.3 with A =[k], x =1,andy = x. Deﬁning W

[k]

(x, t, , d) as

Words 197

the generating function for k-ary words according to length n and the statistic

→

=(ris(w), lev (w), dro(w)), we see that

[k]

(x, r, , d)=1+



j=1

(1−x(−r))

j−1

(1−x(−d))

1 − dx



j=1

(1−x(−r))

j−1

(1−x(−d))

=1−

1 −

1−x(−r)

1−x(−d)

r − d

1−x(−r)

1−x(−d)

In particular, the generating functions for the number of k-ary words avoiding

the subword patterns 11 and 12, respectively, are given by

[k]

(x)=W

[k]

(x, 1, 0, 1) =

1+x

1 − (k − 1)x

=(1+x)



n≥0

(k − 1)

and

[k]

(x)=W

[k]

(x, 0, 1, 1) = 1/(1 − x)



n≥0



n + k − 1



wherewehaveused (A.3) for AW

[k]

(x). Thus we obtain immediately that the

number of k-ary words of length n that avoid 11 or 12, respectively, is given

[k]

(n)=k(k − 1)

n−1

and AW

[k]

(n)=



n + k − 1



Note that these results can be derived easily by direct combinatorial arguments.

More generally, we can use the results of Chapter 5 by setting A =[k],

x =1,andy = x to obtain several known results on k-ary words containing

or avoiding subword patterns of length three proved by Burstein and Mansour

[33, 34].

Example 6.6 Theorem 4.32 gives that the generating function for the number

of k-ary words of length n that contain the subword pattern 111 exactly r times

is given by

111

[k]

(x, q)=

1+q(1 + q)(1 − x)

1 − (k − 1+x)q − (k − 1)(1 − x)q

That is, we recover the results of [33, Example 2.2] and [34, Theorem 3.1].

Likewise, Theorem 4.35 gives that the generating function (after simpliﬁcat-

ion) for the number of k-ary words of length n that contain the subword pattern

112 exactly r times is

112

[k]

(x, q)=

(1 − q)x

(1 − q)x − 1+(1−(1 − q)x

)

198 Combinatorics of Compositions and Words

giving the result of [34, Theorem 3.2]. In addition, for q =0we obtain the

generating function for the number of words of length n that avoid the subword

pattern 112 as

112

[k]

(x)=

x − 1+(1− x

)

which was originally proved in [33, Theorem 3.10].

We conclude the study of subword patterns of length three by considering

the pattern peak, which was studied for compositions in [92]. The result on

the pattern peak given in Theorem 4.26 does not allow for easy substitution to

obtain a result for words, so we derive the generating function for the number

of words that contain the pattern peak directly.

Theorem 6.7 Let W

peak

[k]

(x, q) be the generating function for the number of

k-ary words of length n according to the number of peaks (occurrence of the

subwords 121, 132,or231).Then

peak

[k]

(x, q)=

1+(1+x − xq)(W

peak

[k−1]

(x, q) − 1)

1 − x − x(x +(1− x)q)(W

peak

[k−1]

(x, q) − 1)

for all k ≥ 1, with initial condition W

peak

[0]

(x, q)=1.

Proof Assume k ≥ 1andletw ∈ [k]

. Then either w does not contain the

letter k, w = k, w = w

(1)

k, w = kw

(2)

,orw = w

(1)

(2)

,wherew

(1)

is a

nonempty word on the alphabet [k − 1] and w

(2)

is a nonempty word on the

alphabet [k]. Adding the contributions to the generating function from each

case results in

peak

[k]

(x, q)=W

peak

[k−1]

(x, q)+x + x(W

peak

[k−1]

(x, q) − 1)

+x(W

peak

[k]

(x, q) − 1) + G

(x, q), (6.1)

where G

(x, q) is the generating function for the number of k-ary words w of

length n according to the number of peaks such that w = w

(1)

(2)

and w

(1)

and w

(2)

are nonempty words on the alphabets [k − 1] and [k], respectively.

Now we consider the words of the form w

(1)

(2)

and apply the same de-

composition to the nonempty word w

(2)

, with the same ﬁve cases. Therefore,

(x, q)=xq(W

peak

[k−1]

(x, q) − 1)

+ x

peak

[k−1]

(x, q) − 1)

q(W

peak

[k−1]

(x, q) − 1)

+ x

peak

[k−1]

(x, q) − 1)(W

peak

[k]

(x, q) − 1)

+xq(W

peak

[k−1]

(x, q) − 1)G

(x, q).

Solving for G

(x, q) and substituting the resulting expression into (6.1), we

obtain that

peak

[k]

(x, q)=

1+(1+x − xq)(W

peak

[k−1]

(x, q) − 1)

1 − x − x(x +(1− x)q)(W

peak

[k−1]

(x, q) − 1)

Words 199

which completes the proof. 2

Example 6.8 Using the recursion given in Theorem 6.7, we may obtain the

generating functions for the ﬁrst few values of k using Mathematica or Maple

peak

[1]

(x, q)=

1 − x

peak

[2]

(x, q)=

1 − (q − 1)x

1 − 2x − (q − 1)x

+(q − 1)x

peak

[3]

(x, q)=

−1+3q



− q

2

−1+3x +3q



− 4q



− q

2

+ q

2

and

peak

[4]

(x, q)=



1 − 6q



+5q

2

− q

3



(1 − 4x −6q



+10q



+5q

2

− 6q

2

− q

3

+ q

3

)

where q



= q − 1.

We summarize the results for words containing a single subword pattern τ of

length three in Table 6.1 by giving the complete list of the generating functions

[k]

(x, q) together with the reference where those results ﬁrst appeared. By

setting q = 0, we obtain the corresponding results for AW

[k]

(x).

Similarly, results on longer subword patterns (see Theorems 4.35, 4.37 and

4.39) give the corresponding results for words [34]. We present the example

of the complementary patterns 1

−1

2and2

−1

1 that are not Wilf-equivalent

for compositions, but are Wilf-equivalent for words.

Example 6.9 In Theorem 4.35 the generating functions C

−1

[k]

(x, y, q) and

−1

[k]

(x, y, q) diﬀer, but we have for W

[k]

(x, q)=C

[k]

(1,x,q) that

−1

[k]

(x, q)=

1 − x



k−1

j=0

(1 − x

−1

(1 − q))

= W

−1

[k]

(x, q).

We next consider subsequence patterns, ﬁrst giving the classiﬁcation ac-

cording to Wilf-equivalence, and then giving results on generating functions.

6.4 Subsequence patterns – Classiﬁcation

For 3-letter permutation patterns, the complement and reversal maps in-

duce exactly two symmetry classes, namely

{123, 321} and {132, 231, 312, 213}.

200 Combinatorics of Compositions and Words

TABLE 6.1: W

[k]

(x, q) for 3-letter subword patterns τ

τ W

[k]

(x, q) Reference

111

1+(1− q)x(1 + kx) − (1 − q)(k − 1)x

1 − (k − 1+q)x − (k − 1)(1 − q)x

[33, Thm 2.1]

112

1 − q

1 −

− q +

(1 − x

(1 − q))

[33, Thm 3.10]

212

1 − x − x



j=0

1+jx

(1−q)

[33, Thm 3.12]

213

1 − x − x



k−2

i=0



j=0

(1 − jx

(1 − q))

[34, Thm 3.4]

123

1 − kx −



j=3

(−x)





(1 − q)

j/2

j−3

(q)

[34, Thm 3.3]

where U

(q)=U

(q)=1,

(q)=(1− q)U

2j−1

(q) − U

2j−2

(q),

2j+1

(q)=U

(q) − U

2j−1

(q),

and



j≥0

(q)t

1+t + t

1+(1+q)t

+ t

Burstein [31] proved analytically that 123 ∼ 132 through equality of their

respective generating functions, which implies that there is only one Wilf-

equivalence class for permutation patterns of length three. This equivalence

can also be recovered from the result by Savage and Wilf on compositions

given in Theorem 5.7.

Secondly, for patterns of length three with repeated letters the complement

and reversal maps induce three symmetry classes, namely {111}, {121, 212},

and {112, 211, 221, 122}. The equivalence 112 ∼ 121 for words was ﬁrst shown

by Burstein and Mansour [33] and can also be obtained as a special case of

the same equivalence for compositions given in Theorem 5.10. An even more

general result that has this equivalence as a special case has been proved

by Jel´ınek and Mansour [104] (see Theorem 6.19). No further reductions are

possible as all patterns belonging to a speciﬁc equivalence class have to consist

of the same letters. We summarize this analysis in Table 6.2, where each class

is given by its representatives (up to symmetry).

TABLE 6.2: Wilf-equivalence classes for patterns of length 3

111 112 ∼ 121 123 ∼ 132

Words 201

We will now classify longer patterns according to their Wilf-equivalence,

presenting the results of Jel´ınek and Mansour. To do so, we need the following

deﬁnition.

Deﬁnition 6.10 We deﬁne the content of a word w to be the unordered mul-

tiset of the letters appearing in w. We say that two patterns τ and τ



are

strongly equivalent, denoted by τ

∼ τ



, if for every k and n there is a bi-

jection f between AW

[k]

(τ) and AW

[k]

(τ



) with the property that for every

w ∈AW

[k]

(τ),thewordf(w) has the same content as w, that is, f (w) can

be obtained from w by a suitable rearrangement of the letters.

Clearly, if two patterns are strongly equivalent then they are also Wilf-

equivalent for either words or compositions. Each pattern is strongly equiva-

lent to its reversal, and if two patterns τ and τ



are strongly equivalent, then

their complements c(τ)andc(τ



) are strongly equivalent as well. Note that

τ and c(τ) are usually not strongly equivalent. In order to derive results on

strong equivalence, we introduce a matrix representation of a word.

Deﬁnition 6.11 Let w be a k-ary word of length n. We deﬁne M(w, k) to be

the k × n matrix with a 1 in row i and column j if and only if the j-th letter

of w is equal to i,and0 otherwise. We assume that the rows of a matrix are

numbered bottom to top, and the columns are numbered left to right.

Example 6.12 Let w = 124123 be a word on the alphabet [5].Then

M(w, 5) =

⎡

⎢

⎣

000000

001000

000001

010010

100100

⎤

⎥

⎦

that is, the nonzero entries in the bottom (=ﬁrst) row indicate the positions

of the 1s, and the position of the nonzero entries in the top (= 5-th) row of

the matrix indicate the positions of the 5s.

With this representation, we may use known bijections on ﬁllings of Ferrers

diagrams to obtain new equivalences for words.

Deﬁnition 6.13 A Ferrers diagram is an array of cells whose columns have

nonincreasing length, and the bottom cells of the columns appear in the same

row. A ﬁlling of a Ferrers diagram is an assignment of zeros and ones into

its cells such that every column has exactly one cell containing a 1,whichwe

refer to as a 1-cell.

Note that we usually only depict the 1-cells in a ﬁlling of a Ferrers diagram

for easier readability. Figure 6.1 shows two Ferrers diagrams.

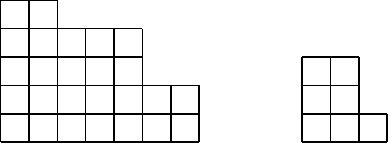
202 Combinatorics of Compositions and Words

FIGURE 6.1: Two Ferrers diagrams.

Deﬁnition 6.14 A ﬁlling of a Ferrers diagram F contains amatrixM if F

can be transformed via deletion of rows and columns to a rectangular diagram

with a ﬁlling and size identical to M ;otherwise,F avoids M .Twomatrices

M and M



are Ferrers-equivalent if for every Ferrers diagram F the number

of M-avoiding ﬁllings is equal to the number of M



-avoiding ﬁllings; they are

strongly Ferrers-equivalent if for every Ferrers diagram F there is a bijection

between M -avoiding and M



-avoiding ﬁllings of F that preserves the number

of 1-cells in each row.

Example 6.15 Let

⎡

⎣

1000

0011

0100

⎤

⎦

and M

Then the Ferrers diagram F

of Figure 6.1 contains M

,asF

can be trans-

formed into M

via deletion of columns four, six and seven, and rows four

and ﬁve. On the other hand, there are no choices of row and column deletions

that will transform the Ferrers diagram F

into M

In order to describe the connection between Ferrer’s ﬁllings and words, we

need the following notation.

Deﬁnition 6.16 For a word w ∈ [k]

and an integer ,weletw +  denote

the word obtained by increasing each letter of w by . We also denote the

concatenation of the words w and w



by ww



Lemma 6.17 Let τ and τ



be two patterns on k letters, and let ρ be a pattern

on  letters. If M (τ, k) and M(τ



,k) are strongly Ferrers-equivalent, then the

two patterns τ(ρ + k) and τ



(ρ + k) are strongly equivalent on the alphabet

[k + ].

Proof Let ν = τ(ρ + k)andν



= τ



(ρ + k). For given m and n,choose

awordw ∈AW

[m]

(ν), and let M = M(w, m) be its corresponding matrix.

Clearly, since w avoids ν, M avoids the matrix M(ν, k + ). Now color the

cells of M red and green, where a cell c is green if and only if the submatrix

Words 203

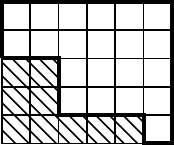
of M strictly to the right and strictly above c contains M(ρ, ). All other

cells are colored red. Figure 6.2 shows the coloring for the word 534212 with

τ = 21, ρ = 1 (and therefore ν = 213), where the striped part corresponds to

the color green.

FIGURE 6.2: Coloring of the Ferrers diagram for the word 534212.

Note that the green cells form a Ferrers diagram (why?) and that the

nonzero columns of this diagram induce an M (τ,k)-avoiding ﬁlling. Using

the strong Ferrers-equivalence of M (τ,k)andM(τ



,k), we may transform

this ﬁlling into a M(τ



,k)-avoiding ﬁlling. This operation transforms M into

amatrixM



representing a ν



-avoiding word w



with the same content as w.

To see that this operation can be inverted, observe that the operation has

only modiﬁed the ﬁlling of the green cells of M. Also, for every green cell c of

M there is a copy of M (ρ, ) strictly to the right and strictly above c which

consists only of red cells. Thus the red cells of M coincide with the red cells

of M



and we have found a bijection showing that ν

∼ ν



. 2

Lemma 6.17 allows us to translate results about ﬁllings of Ferrers diagrams

into results about words. Using known results about Ferrers-equivalence [58,

104, 127], we obtain the following results valid for any pattern ρ.

Proposition 6.18 For k ≥ 1, M(12 ···k, k) is strongly Ferrers-equivalent to

M(k(k − 1) ···1,k)(see [127, Theorem 13] ). This implies that

12 ···k(ρ + k)

∼ k(k − 1) ···1(ρ + k).

Proposition 6.19 For i, j ≥ 0, M (2

, 2) is strongly Ferrers-equivalent to

M(12

i+j

, 2) (see [104, Lemma 39] ). This implies that

(ρ +2)

∼ 12

i+j

(ρ +2).

These results do not account for all the equivalences among subword pat-

terns of small length. For example, the pattern 132 does not have one of

the above structures. To complete our classiﬁcation we need another lemma

whose proof uses an idea that has been previously applied in the context of

pattern-avoiding set partitions [104, Theorem 48].

204 Combinatorics of Compositions and Words

Theorem 6.20 For any t ≥ 3,allpatternsthatconsistofasingle1,asingle

3 and t − 2 letters 2 are strongly equivalent.

Proof Let t be ﬁxed. Let τ(i, j) denote the word of length t where the i-th

letter is a 1, the j-th letter is a 3, and the remaining letters are equal to 2.

Our aim is to show that all the patterns in the set {τ(i, j),i = j, 1 ≤ i, j ≤ t}

are strongly equivalent. Since each word is strongly equivalent to its reversal,

we only need to deal with the words τ(i, j)withi<j. Proposition 6.19 gives

immediately that the words {τ(i, t),i=1, 2,...,t−1} (those with a 3 at the

end) are all strongly equivalent. Using the complement and reversal maps

we can derive that the words {τ (1,j),j =2, 3,...,t} (those with a 1 at the

beginning) are also strongly equivalent.

To prove the theorem, it suﬃces to show that for every i<j<t,theword

τ(i, j) is strongly equivalent to the word τ(i +1,j+1). Let m be an integer.

We will say that a word w c

ontains τ(i, j) at level m if there is a pair of letters

, h with <m<hsuch that the word w contains a subsequence s on the

alphabet {, m, h} such that s is order-isomorphic to τ(i, j). For example, the

word 132342 contains the pattern 1223 at level three (due to the subsequence

1334), while it avoids 1223 at level two.

Assume now that we are given a ﬁxed pair of indices i and j,withi<j<t,

and we want to provide a content-preserving bijection between τ(i, j)-avoiding

and τ(i +1,j+ 1)-avoiding words of length n. We will say that a word w is

an m-hybrid if for every

m<m,thewordw avoids τ(i, j) at level m, while

for every 8m ≥ m, w avoids τ(i +1,j+1)atlevel 8m. We will present, for any

m ≥ 1, a content-preserving bijection between m-hybrids and (m+1)-hybrids.

By composing these bijections we obtain the required bijection between τ(i, j)-

avoiding and τ(i +1,j+ 1)-avoiding words.

Let m ≥ 1beﬁxedandletw be an arbitrary word. A letter of w is called

low if it is less than m, and a letter is called high if it is greater than m.Alow

cluster of w is a maximal block of consecutive low letters of w.Ahigh cluster

is deﬁned analogously. Thus every letter of w diﬀerent from m belongs to a

unique high or low cluster. The landscape of w is a word over the alphabet

{L,m,H} obtained by replacing every low cluster of w by a single symbol L

and every high cluster of w by a single symbol H. For example, the word

w = 534212 has landscape HmHL for m = 3, with two high clusters 5 and

4 and a single low cluster 212. Note that w contains τ(i, j) at level m if and

only if the landscape of w contains the subsequence m

i−1

j−i−1

t−j

We will now describe the bijection between m-hybrids and (m +1)-hybrids.

Let w be an m-hybridwordandletX be its landscape. We split X into three

parts, X = PmS, where the preﬁx P is formed by the letters of X that appear

before the ﬁrst occurrence of m in X, and where the suﬃx S is formed by

the letters that appear after the ﬁrst occurrence of m.LetX



= SmP.Then



contains a subsequence m

i−1

j−i−1

t−j

if and only if X contains a

subsequence m

j−i−1

t−j−1

.SinceX is the landscape of a word that