Henini M. Handbook of Self Assembled Semiconductor Nanostructures for Novel devices in Photonics and Electronics
Подождите немного. Документ загружается.

GaSb/GaAs Quantum Nanostructures by Molecular Beam Epitaxy 279
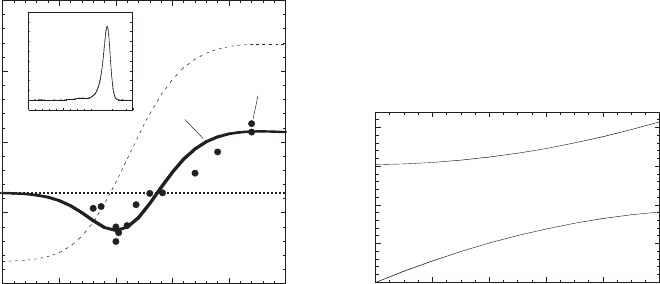
For a comparison, the calculated result by using a model solid theory [48] is also indicated by
the broken line in Fig. 8.7 a. The optical transition energy calculated by the model solid theory
increases with the temperature of cap growth and does not show the minimum value at about
350°C. The deviation between the calculated energy and experimental one was about 40 meV at
350°C.
Figure 8.7 b shows the conduction band edge ( E
c
) and valence band edge ( E
v
), calculated from
the obtained b
v
0.67. Here, both band edges include a strain effect. The obtained b
v
0.67 is
smaller than that reported by Liu et al. [47] (1.08) and indicates a bowing effect in not only the
valence band edge but also in the conduction band edge, as shown in Fig. 8.7 b. This difference is
mainly due to the different QW structures: the rectangular QW potential without the broadening
of the Sb composition was used in the previous reports. In our analysis, the broadened QW struc-
tures due to the Sb–As segregation effect are taken into consideration, as explained above. As a
result, we can empirically determine the added bowing parameter of b
v
(0.67 0.06), which is
independent of the Sb composition and the QW structure.
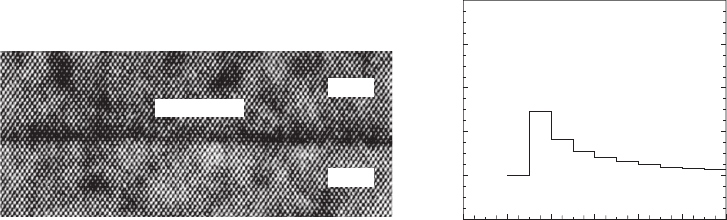
Figure 8.8 a shows a (110) cross-sectional high-resolution transmission electron microscopy
(HRTEM) image of the GaSb (1 ML)/GaAs QW, grown at 470°C. In this image, intermixing of Sb
atoms in the GaAs capping layer is observed, and the width of the QW is roughly estimated to be
about 3 ML. Figure 8.8 b shows the Sb-composition profi le of the GaSb (1 ML)/GaAs QW, calcu-
lated for 470°C using the presented kinetic model with the above fi tting parameters ( b
v
0.67,
E
Sb
1.68 eV and E
As
1.80 eV). The Sb composition decreases to less than 0.1 for a thickness
of more than 3 ML. The calculated QW width is comparable to the experimental one.
On the basis of these results, it is concluded that the presented kinetic model that includes the
Sb–As surface exchange reaction is effective for analysing the MBE growth of the GaSb/GaAs het-
erointerface structures. For the activation energies of the Sb–As exchange reaction, Magri and
Zunger obtained E
Sb
1.68 eV and E
As
1.75 eV from the analysis of the InAs/GaSb superlat-
tice [49] . As presented above, for the GaAs/GaSb QWs, the almost same E
Sb
(1.68 0.01 eV) was
obtained, and E
As
was about 50 meV higher (1.80 0.01 eV). It is possible that the difference
in the value of E
As
is caused by the different binding energies of InAs and GaAs.
(b)
calculation
Energy (eV)
1.30
1.45
470°C
12 K
PL intensity
QW (1 ML)
(No segregation)
Model
solid theory
(a)
PL
1.3
1.35
1.4
1.45
1.5
250
Growth temperature (°C)
Optical transition energy (eV)
300 350 400 450
500
Sb composition x
E
c
0.5
1.0
2.0
1.5
Energy (eV)
E
v
0
0 0.2 0.4 0.6 0.8 1.0
1.35
1.40
Figure 8.7 (a) Experimental PL (12 K) results and calculated ones of optical transition energy obtained from the
GaSb (1 ML)/GaAs QWs as a function of the growth temperature of the GaAs cap layer. The growth rate of the cap
layer was 0.14 nm/s. The solid line indicates calculated transition energy of GaSb/GaAs QW structures, analysed
using the kinetic model with fi tting parameters of b
v
0.67, E
Sb
1.68 eV and E
As
1.80 eV. A broken line
indicates the results calculated using a model solid theory [48] . (b) Calculated conduction and valence band edges
( E
c
and E
v
) for strained GaAs
1
x
Sb
x
(12 K) as a function of Sb composition. The obtained b
v
0.67 was used in
this calculation.
CH008-I046325.indd 279CH008-I046325.indd 279 6/25/2008 2:30:06 PM6/25/2008 2:30:06 PM
280 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics
8.3 GaSb quantum dots on GaAs
GaSb quantum dots (QDs) on GaAs are spontaneously formed by Stranski–Krastanov (SK)
growth mode because GaSb on GaAs has a lattice-mismatched interface ( Δ a
0
/ a 7.8%) simi-
lar to InAs on GaAs. In this section, we will discuss the self-assembled GaSb/GaAs QDs grown
by molecular beam epitaxy (MBE) using the SK mode. The formation of three-dimensional (3D)
GaSb islands on GaAs(001) will be described in Section 8.3.1. Then, optical properties of ensem-
ble GaSb/GaAs QDs and single GaSb/GaAs QD will be discussed at in Section 8.3.2.
8.3.1 MBE growth of self-assembled GaSb/GaAs quantum dots
Thin fi lm growth on a bulk substrate is typically classifi ed by three growth modes; Frank–van
der Merwe (FM) mode exhibiting layer-by-layer growth, Volmer–Weber (VM) mode forming 3D
islands and Stranski–Krastanov (SK) mode. The SK mode is a combination of the FM and VW
modes; the 3D island growth occurs followed by the 2D growth. The growth mode transition
from 2D to 3D growth is induced by the difference in the surface energy between the grown
material and the substrate and by strain energy due to lattice mismatch between both materi-
als. In the case of GaSb growth on GaAs, the SK growth frequently occurs, and such 3D islands
of GaSb/GaAs have been expected as type II QD structures. The self-assembled GaSb/GaAs QDs
based on the SK mechanism have been studied recently [50–53] .
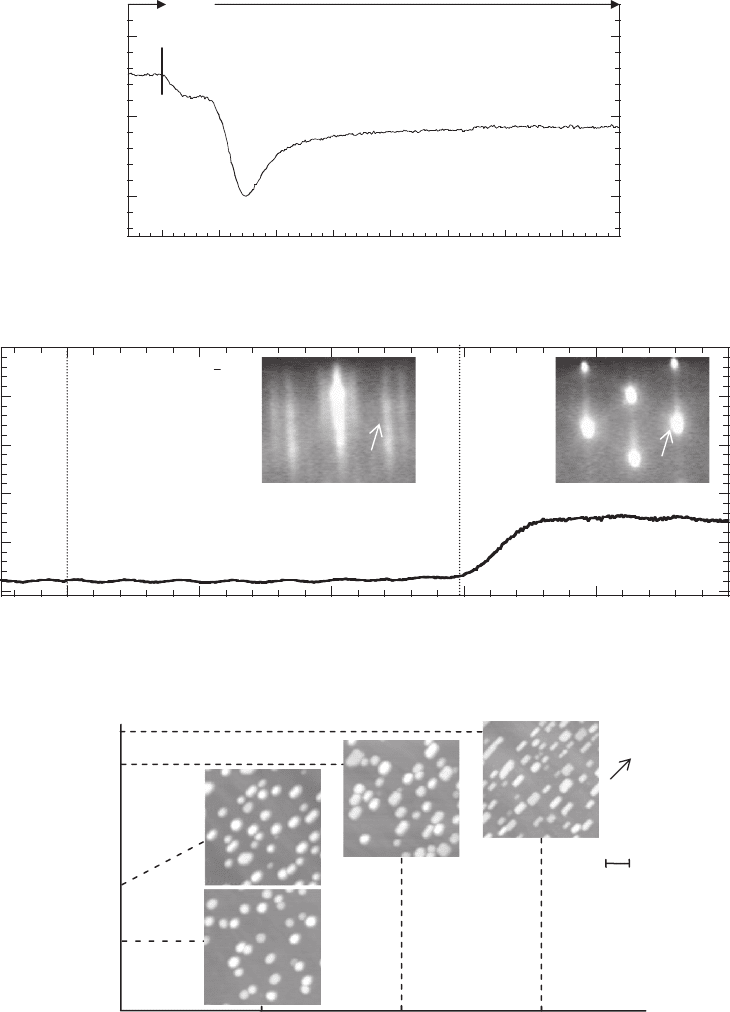
The typical growth process of GaSb/GaAs QDs is described as follows. First, prior to the GaSb
growth on GaAs, Sb
4
fl ux is irradiated on the GaAs buffer layer to fabricate initial GaSb surface
layer. Figure 8.9 shows RHEED intensity of a specular beam as a function of irradiation time of
Sb
4
fl ux. After the GaAs buffer layer growth at 580°C, the substrate temperature was dropped to
470°C. Then Sb
4
fl ux was irradiated on the GaAs surface instead of As
4
fl ux. During the Sb
4
irra-
diation, RHEED pattern changes from c (4 4) to (1 3) reconstruction, which reveals the Sb-
terminated Ga(As)Sb surface. In Fig. 8.9 , the RHEED specular beam intensity decreases and then
saturates. This intensity saturation means the preparation of the stable Sb-terminated Ga(As)Sb
surface layer. More recently, this surface layer structure has been analysed by in situ X-ray crystal
truncation rod (CTR) scattering measurements [31] .
Next, on this Ga(As)Sb surface layer, GaSb QDs were grown at 470°C. Figure 8.10 shows a
relationship between RHEED diffraction beam intensity and GaSb growth time. As the GaSb
growth proceeds, the RHEED pattern changes from streak to spot pattern. It means the growth
mode transition from 2D to 3D growth; SK growth mode. The RHEED intensity is almost kept
constant for the 2D growth and then rapidly increases for the 3D growth, as shown in Fig. 8.10 .
The critical thickness for 2D–3D transition can be estimated by using this time dependence of
GaSb-QW
GaAs
GaAs
(a)
(b)
0
8
Thickness (ML)
Sb composition
0
0.2
0.4
0.6
24
6
Figure 8.8 (110) cross-sectional HRTEM image (a) and calculated Sb composition profi le (b) of GaSb (1 ML)/
GaAs QW. The growth temperature and the growth rate of the GaAs capping layer were 470°C and 0.14 nm/s,
respectively. Fitting parameters b
v
0.67, E
Sb
1.68 eV and E
As
1.80 eV were used in this calculation.
CH008-I046325.indd 280CH008-I046325.indd 280 6/25/2008 2:30:07 PM6/25/2008 2:30:07 PM
GaSb/GaAs Quantum Nanostructures by Molecular Beam Epitaxy 281
RHEED intensity. The critical thickness usually depends on the GaSb growth condition. The dif-
ference in critical thickness is possible to relate to Sb–As intermixing during growth.
Figure 8.11 shows AFM images of GaSb QDs grown on Sb-initiated GaAs at various growth
conditions. In the conventional SK growth, the change of the growth conditions modifi es the
Sb open
Sb irradiation time (sec)
40 030
20
10
RHEED specular beam
intensity (arb. units)
c(4 4) (1×3)
Figure 8.9 RHEED specular beam intensity as a function of irradiation time of Sb
4
fl ux on GaAs(001) surface.
0
GaSb
g
rowth time (sec)
RHEED intensity (arb. units)
[110]
azimuth
2D growth
3D growth
Ga open
10 20 30 40 50
Figure 8.10 Two typical RHEED patterns for 2D and 3D growth stages and RHEED diffraction beam intensity as
a function of the growth time during MBE growth of GaSb on GaAs(001).
0.5
1.0
2.2
3.0
Sb
4
pressure (×10
7
torr)
100 nm
(110)
0.04 0.08 0.16
Growth rate (monolayer/sec)
0
Figure 8.11 AFM images of GaSb QDs grown on Sb-initiated GaAs at various growth conditions.
CH008-I046325.indd 281CH008-I046325.indd 281 6/25/2008 2:30:07 PM6/25/2008 2:30:07 PM

282 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics
3D structures and density. For high growth rate and high Sb
4
pressure, the dot density increases,
and size fl uctuation becomes large. In addition, the dot shape is anisotropy: the lateral size elon-
gates along the
[110] direction. As the growth rate and the Sb
4
pressure decrease, the surface
migration is enhanced. As a result, size fl uctuation and dot density decrease. The QD structure
reveals a dome-like shape. Figure 8.12 shows cross-sectional scanning transmission electron
microscope (STEM) images of GaSb QDs grown at two typical growth conditions: growth rate
of 0.16 ML/s and Sb
4
pressure of 2.2 1 0
7
torr (a), 0.04 ML/s and 0.5 1 0
7
torr (b). These
QDs were embedded into GaAs matrix. STEM images of both samples show the presence of the
wetting layer. In the anisotropic large dot (a), misfi t dislocations are observed at the GaSb/GaAs
heterointerface [54] . Hence, the strain of the QD is relaxed. Such interface misfi t dislocations are
frequently formed under high Sb pressure [55] and high growth rate conditions. On the contrary,
in the dome-like dot with small size (b), no dislocations are observed. Low Sb pressure and low
growth rate are preferable conditions for getting coherent GaSb QDs with isotropic shape and
high size uniformity.
GaAs
GaSb QD
GaAs
(a) (b)
20 nm
Figure 8.12 Cross-sectional STEM images of GaSb QDs grown at two typical growth conditions: growth rate
of 0.16 ML/s and Sb
4
pressure of 2.2 1 0
7
torr (a), 0.04 ML/s and 0.5 1 0
7
torr (b). STEM images were
acquired by a high-angle annular dark fi eld (HAADF) mode.
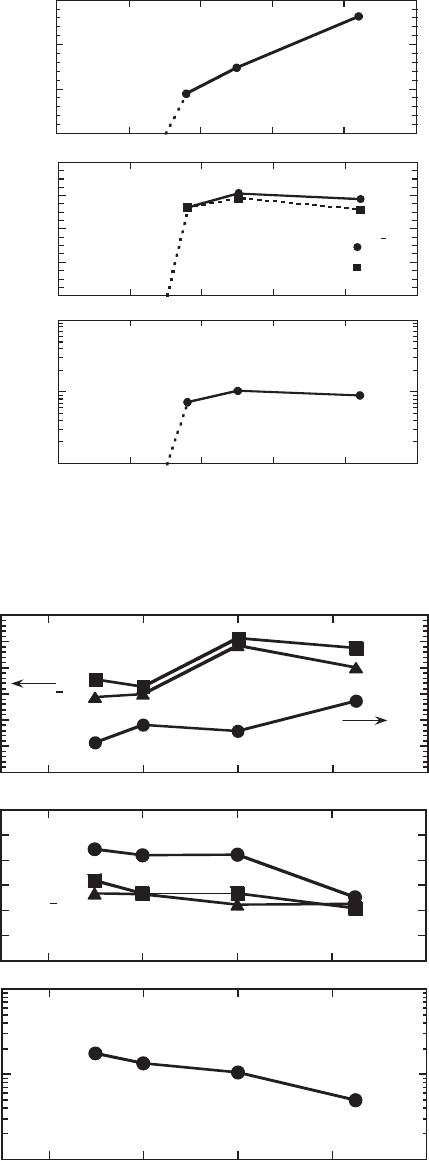
Figure 8.13 shows GaSb coverage dependences of the QD size (height (a) and lateral size (b))
and density (c). GaSb growth conditions were low growth rate of 0.04 ML/s and low Sb
4
pressure
of 0.5 1 0
7
torr. Here, the QD size was measured by using AFM, which shows large lateral size
because of tip curvature. The lateral size and dot density tend to saturate at more than about
3 ML in coverage. In the case of InAs SK growth on GaAs, self size-limiting phenomena due to
the strain and facet formation have been observed under low growth rate and low arsenic pres-
sure conditions [56] . However, for the GaSb QDs on GaAs, the stable facet did not clearly appear
on the side wall. In addition, as the growth proceeded, the dot height increased and did not satu-
rate, as shown in Fig. 8.13 a. It is possible that the saturation of the lateral size is caused by the
strain at the island edge. At the step sites of the dot edge, the compressive strain increases with
increasing dot size [57] . Consequently, the lateral size is limited by inhibition of adatom incorpo-
ration. On the contrary, the adatom incorporation occurs actively at the top of the dot because
of the lattice relaxation at the top area. So, the dot height increases with the GaSb coverage.
Although the self-limiting effect of height does not occur, size fl uctuation in height can be sup-
pressed by preparing high aspect ratio in the QD structure.
Figure 8.14 shows the average QD size (a), standard deviation (b) and density (c) as a function
of the growth temperature of the GaSb QDs. The GaSb coverage was 4.5 ML. As the substrate
temperature increases, the dot size increases and the dot density decreases. It is attributed to
enhancement of the surface migration for high substrate temperature. The long surface migra-
tion is favourable for suppression of the size fl uctuation. Indeed, the standard deviation reduces
with increase in the substrate temperature, as shown in Fig. 8.14 b. Figure 8.15 shows size dis-
tributions of the GaSb QDs grown under low growth rate of 0.04 ML/s, low Sb
4
pressure of
0.5 1 0
7
torr and substrate temperature of 470°C. The GaSb coverage was 5 ML, and the QD
density was 8.9 1 0
9
c m
2
. The standard deviations were 9.2% for the lateral size and 14% for
the height. After their GaSb QDs were embedded in the GaAs capping layer, PL properties were
measured as follows.
CH008-I046325.indd 282CH008-I046325.indd 282 6/25/2008 2:30:08 PM6/25/2008 2:30:08 PM
0
20
40
60
80
Average lateral
size (nm)
(110)
(110)
(b)
10
9
10
10
10
11
1
Dot density (cm
2
)
GaSb coverage (ML)
(c)
0
5
10
15
Average height (nm)
(a)
234 56
Figure 8.13 GaSb coverage dependences of QD height (a), lateral size (b) and density (c). GaSb growth rate was
0.04 ML/s. Sb
4
pressure was 0.5 1 0
7
torr.
10
20
30
40
50
60
70
0
5
10
15
20
25
30
Average lateral
size (nm)
Average height (nm)
height
(110)
(110]
(a)
10
9
10
10
10
11
450
Density (cm
2
)
Substrate temperature (°C)
(c)
0
5
10
15
20
25
30
Standard deviation (%)
Height
(110)
(110)
(b)
460 470 480 490
Figure 8.14 Average QD size (a), standard deviation (b) and density (c) as a function of the growth temperature of
GaSb QDs. GaSb coverage was 4.5 ML. GaSb growth rate was 0.04 ML/s. Sb
4
pressure was 0.5 1 0
7
t o r r.
CH008-I046325.indd 283CH008-I046325.indd 283 6/25/2008 2:30:08 PM6/25/2008 2:30:08 PM
284 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics
950
Wavelength (nm)
12K
PL intensity (arb. units)
450°C
470°C
490°C
1000 1050 1100
1150 1200 1250 1300
1350
Figure 8.16 PL spectra of GaSb QDs as a function of growth temperature of GaAs capping layers (490°C, 470°C
and 450°C). Growth conditions of GaSb QDs: growth rate of 0.04 ML/s, Sb
4
pressure of 0.5 1 0
7
torr and
growth temperature of 470°C.
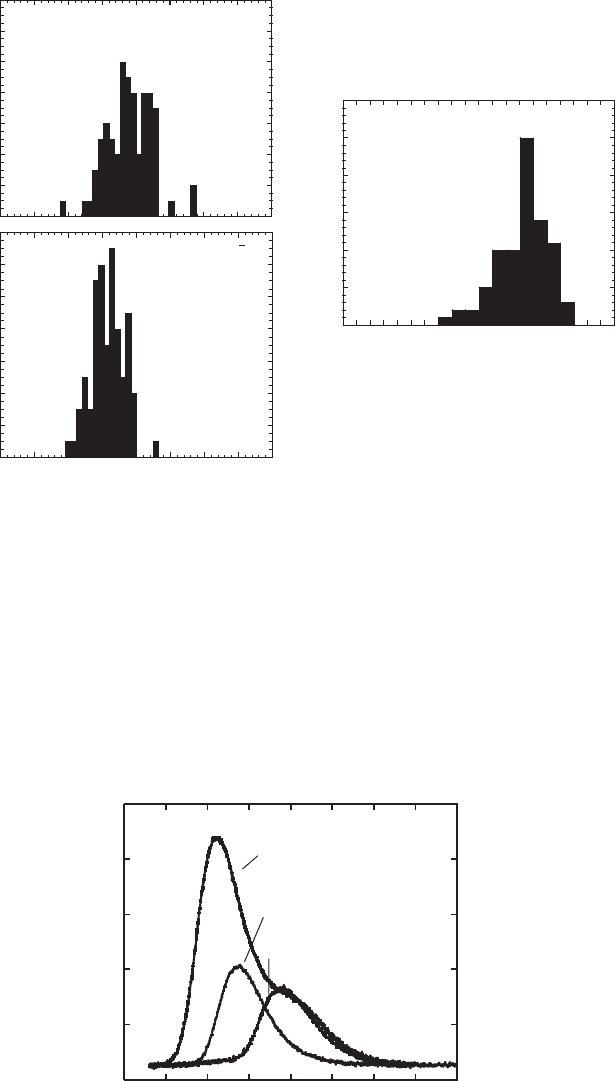
Figure 8.16 shows PL spectra obtained from GaSb QDs as a function of the growth temper-
ature of the GaAs capping layers (490 °C, 470 °C and 450 °C). Growth conditions of the GaSb
QDs were low growth rate of 0.04 ML/s, low Sb
4
pressure of 0.5 1 0
7
torr and 470°C. PL peak
wavelength reveals a blue shift as the growth temperature increases. In the case of the 490 °C
growth, the RHEED pattern changed from spot pattern into streak one during the growth inter-
ruption between the SK growth and the capping growth. In short, the QD structure changes into
QW-like structure during the growth interruption. For the growth below 470°C, the RHHED
spot pattern was kept until the embedding in the GaAs capping layer. However, reduction of the
0
2
4
6
8
10
12
14
Number
(110)
lateral size (nm)
20
30
40
50
60
70
80
90
100
0
2
4
6
8
10
12
14
Number
(110)
0
5
10
15
20
25
30
0
Height (nm)
Number
510 15 20
Figure 8.15 Size distributions of the GaSb QDs grown under growth rate of 0.04 ML/s, Sb
4
pressure of
0.5 1 0
7
torr and substrate temperature of 470°C. GaSb coverage was 5 ML.
CH008-I046325.indd 284CH008-I046325.indd 284 6/25/2008 2:30:09 PM6/25/2008 2:30:09 PM
GaSb/GaAs Quantum Nanostructures by Molecular Beam Epitaxy 285
QD size and Sb–As intermixing at the heterointerface should be considered during the growth
interruption and the capping growth. These effects induce the blue shift for higher temperature
growth of the capping layer. As mentioned before, the GaSb growth conditions of low growth
rate and low Sb
4
pressure suppress the size fl uctuation of the QDs. In fact, PL spectrum for 470°C
reveals narrow linewidth of 65 meV [53], as compared with that of previous reports.
8.3.2 Optical properties of GaSb/GaAs quantum dots
8.3.2.1 Energy structure of GaSb/GaAs quantum dots
Self-assembled quantum dots (QDs) are an ideal system for studying zero-dimensional quantum
effects [58] while showing promise for future quantum devices [59–61] . So far, many experi-
mental studies have been carried out mainly on self-assembled InAs/GaAs QDs. From the view-
point of the energy level structure, the InAs/GaAs QD has a band alignment classifi ed as type I,
in which both electrons and holes are confi ned within the InAs QD as shown in Fig. 8.17 . Their
wavefunctions show a strong spatial overlap. In a staggered type II band structure, however, the
lowest electron and hole energy states are concentrated on different layers [2, 51, 52, 62–67] . In
a type II GaSb/GaAs QD, the spatial separation is between the electron wavefunction in the GaAs
layer and the hole wavefunction in a GaSb QD. Consequently, the optical properties of a type II
QD differ from those of a type I QD, as described later.
Type II GaSb/GaAs
Type I InAs/GaAs
GaSb
GaAs
InAs GaAs
Figure 8.17 Energy structure of type I InAs/GaAs QDs and type II GaSb/GaAs QDs.
8.3.2.2 Fundamental optical properties of GaSb/GaAs QDs
The characteristic optical properties resulting from the type II band structure have been observed
in various experiments. The inset of Fig. 8.18 shows the macroscopic (ensemble-averaged)
PL spectra of GaSb/GaAs QDs at 10 K [62] . The PL spectra have a broad peak at 1.08 eV
with a full width at half-maximum (FWHM) linewidth of about 80 meV. These broadened
1.070
1.072
1.074
1.076
1.078
1.080
1.082
1.084
1.086
1.088
1.090
Exc. power density (W/cm
2
)
0 5 10 15 20 25
Peak energy (eV)
Energy (eV)
PL intensity (a.u)
21.2 W/cm
2
0.7 W/cm
2
0.4 W/cm
2
2.1W/cm
2
10.6 W/cm
2
7.1 W/cm
2
0.9 1.0 1.1 1.2 1.3
Figure 8.18 Excitation power dependence of the PL peak energy [62] . The inset shows PL spectra at 10 K as
a function of the excitation density. Reprinted with permission from Motlan et al. , Appl. Phys. Lett. 79 , 2976
(2001). Copyright 2001, American Institute of Physics.
CH008-I046325.indd 285CH008-I046325.indd 285 6/25/2008 2:30:09 PM6/25/2008 2:30:09 PM
286 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics
PL spectra arise from the distribution of the optical transition (exciton) energies in the indi-
vidual QDs due to inhomogeneities in properties such as size, strain, and composition. The
resultant broadened spectral linewidth is therefore referred as “ inhomogeneous linewidth ” .
Figure 8.18 shows the excitation power dependence of the PL peak energy and the inset shows
the PL spectra as a function of excitation density. A higher energy shift (blue shift) of the PL max-
imum ( ⬃ 12 meV) is observed with increasing excitation density from 0.4 to 10.6 W/cm
2
. Such a
blue shift is characteristic of type II structures [62, 64, 65] . In type I InAs/GaAs QDs, the lowest
PL peak arising from exciton ground state shifts at lower energies with an increase in the excita-
tion density [68] . Based on the macroscopic PL measurements, it was speculated that the blue
shift of the peak arises from change of the band bending occurring at the interfaces where the
electrons accumulate [62] .
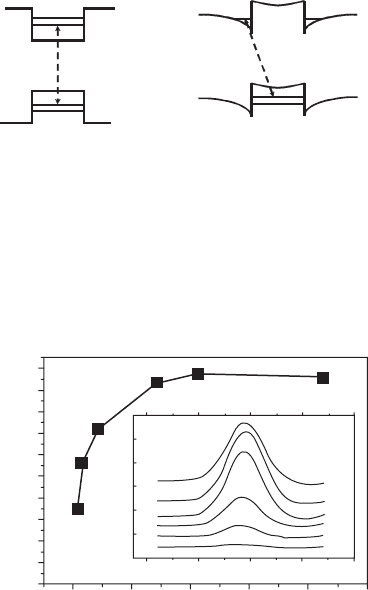
In addition to the characteristic blue shift of the PL peak, the recombination dynamics of
the exciton in type II QDs is much different from that in the type I. Figure 8.19 presents the PL
decay curves at 10 K, for different excitation intensities [2] . Under the lowest excitation condi-
tion (I/10), the PL dynamics can be viewed as a single-exponential decay with a time constant
of 23 ns. This measured lifetime, arising from the reduced spatial overlap between electron and
hole wavefunctions, is much longer than the typical radiative lifetime of type I InAs/GaAs QDs
( ⬃ 1 ns) [69] . This means the reduced recombination probability; that is, the exciton transition
has a smaller oscillator strength.
20
0 20406080100
Time (ns)
10
2
10
3
10 I
I
I/10
10
4
Normalized number of photon
Figure 8.19 PL decay curves of GaSb QDs at 10 K with different excitation intensities [2] . The data are normalized
with the tail parts of the decay curve. Reprinted with permission from C.-K. Sun et al. , Appl. Phys. Lett. 68 , 1543
(1996). Copyright 1996, American Institute of Physics.
8.3.2.3 Exciton fi ne structures of GaSb/GaAs QDs
The ensemble-averaged optical spectrum has a broad feature that masks the intrinsic nature
of the QD optical properties. Single QD optical spectroscopy, which is spectroscopic observation
of a single QD, is one of the most useful tools in studying these intrinsic properties. The various
approaches to realizing single QD PL spectroscopy have been applied using the conventional opti-
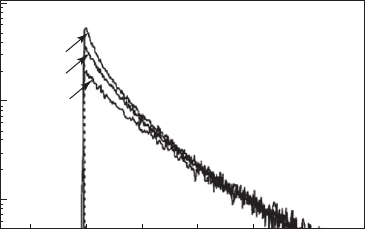
cal microscopes [70] , near-fi eld scanning optical microscopes [71], and so on [72] . Figure 8.20 a
shows typical PL spectra for a single GaSb QD at various excitation power densities, obtained
using a near-fi eld scanning optical microscope [73, 74] . A single and sharp emission peak in
the PL spectrum, denoted by X, is observed at 1.2716 eV under lower excitation power condi-
tions (less than several μ W), while the ensemble-averaged PL spectrum has a broad peak with
a 60 meV linewidth. The PL intensities of the X line as a function of excitation power density
show an almost linear power dependence under lower excitation conditions (see Fig. 8.20 b). The
sharp X emission line, having a less than 1 meV linewidth (FWHM), is assigned to the radiative
recombination of the exciton consisting of a hole confi ned in a GaSb QD and an electron in the
surrounding GaAs barrier layer, which are weakly bound by an attractive Coulomb interaction.
Figure 8.21 shows the PL peaks for exciton emission from three different GaSb QDs on an
expanded energy scale [74] . The linewidths of the three emission peaks are estimated to be less
CH008-I046325.indd 286CH008-I046325.indd 286 6/25/2008 2:30:10 PM6/25/2008 2:30:10 PM
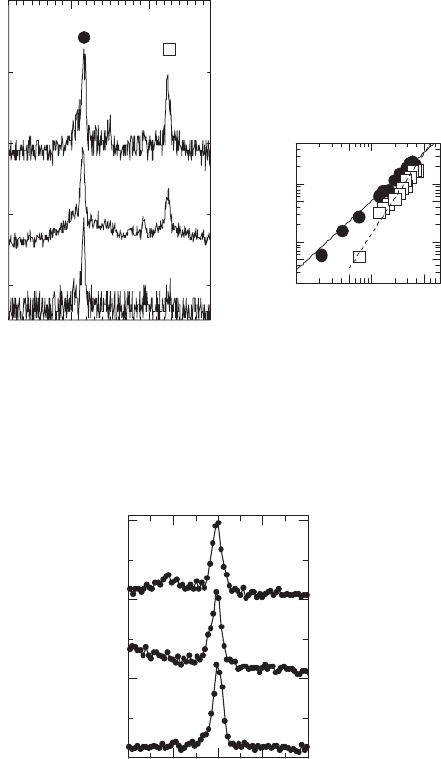
GaSb/GaAs Quantum Nanostructures by Molecular Beam Epitaxy 287
than 250 μ eV. As a consequence, the “ homogeneous line width ” (the intrinsic line width of a sin-
gle QD) of an exciton state in a type II GaSb QD is evaluated as less than 250 μ eV, narrower than
the 280 μ eV theoretically predicted for an ideal quantum well at 8 K [72] .
Furthermore, as seen in Fig. 8.20 a, an additional peak appears at 1.2824 eV in the PL spec-
tra under higher excitation conditions (more than several μ W). This peak, denoted by XX, is
observed about 11 meV on the higher energy side of an exciton emission (X). Figure 8.20 b shows
the nearly quadratic power dependence of the XX line as a function of excitation power. This
power dependence of the PL intensity suggests that the XX emission results from the radiative
transition from a two-exciton state to the exciton ground state. The experimental result of the
two-exciton emission (XX) on the higher energy side of the exciton emission (X) is in contrast the
results commonly reported in type I structures such as in self-assembled In(Ga)As QDs [75, 76]
and naturally occurring GaAs QDs [77, 78] . This is consistent with the behaviour of the macro-
scopic PL spectrum of an ensemble of GaSb QDs, which shows a blue shift of the PL peak with
increasing excitation power (see Fig. 8.18 ) [62] . In type I QDs, the quadratic power dependent PL
1.27 1.28
PL intensity (arb. units)
X
XX
(a) (b)
GaSb
1.25
0.69
5.2 µW
X
XX
10
1
10
0
10
1
10
0
Excitation power (µW)
PL intensity (arb. units)
Photon energy (eV)
QD 8 K
Figure 8.20 (a) PL spectra of a single GaSb QD at 8 K under various excitation power densities. The PL peaks at
1.2716 eV and 1.2824 eV are denoted as X and XX. (b) Excitation power dependence of PL intensities of the X and the
XX line. The solid (dotted) line corresponds to the gradient associated with linear (quadratic) power dependence [74].
Reprinted with permission from K. Matsuda et al. , Appl. Phys. Lett. 90, 013101 (2007). Copyright 2007,
American Institute of Physics.
2 1 0 1 2
Energy (meV)
PL intensity (arb. units)
QD1
QD2
QD3
Figure 8.21 PL spectra of three different QDs in an expanded energy scale [74] . Reprinted with permission from
K. Matsuda et al. , Appl. Phys. Lett. 90, 013101 (2007). Copyright 2007, American Institute of Physics.
CH008-I046325.indd 287CH008-I046325.indd 287 6/25/2008 2:30:10 PM6/25/2008 2:30:10 PM

288 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics
line usually observed at 3 to 5 meV on the lower energy side of the exciton emission is generally
assigned to the bound biexciton emission.
The energy difference between the two exciton emission (XX) and the exciton emission (X) cor-
responds to the binding energy ( E
bin
2E
X
E
XX
), where E
XX
and E
X
are the energies of the two
exciton state and the exciton ground state, respectively. A negative binding energy implies that the
exciton–exciton interaction is repulsive in these QDs. The binding energy of the two exciton state
is determined by summing the repulsive Coulomb interactions between the electrons and between
the holes, and the attractive Coulomb interaction between electrons and holes. Since both
electron and hole wavefunctions are strictly confi ned in a type I QD, all three terms, the electron–
electron, the hole–hole, and the electron–hole Coulomb interactions are of the same order of
magnitude and the delicate balance between them leads to the binding of the two excitons (biex-
citons). The biexcitons acquire a positive binding energy due to interparticle correlations in a
way similar to the formation of a hydrogen molecule. The observed binding energy in type I QDs
is typically 3–5 meV. The situation is quite different in type II GaSb QDs, in which only the holes
are confi ned inside the QD, while the electron wavefunction is relatively delocalized in the GaAs
barrier layer around the QDs. Consequently, because the strengths of the electron–hole and elec-
tron–electron interactions are smaller than that of the hole–hole interaction, it is reasonable for
the Coulomb energy of the two exciton ground state to be dominated by the hole–hole repulsive
Coulomb interaction, and thus the binding energy has a negative value.
8.3.2.4 Many exciton states of GaSb/GaAs QDs
To develop a quantitatively accurate understanding of the exciton and two exciton states in GaSb
QDs, a theoretical calculation based on the empirical pseudopotential model (EPM) was applied
[79] . The single particle states were obtained by solving the one electron Schrödinger equation in
a potential
Vr()
obtained from a superposition of atomic pseudopotentials
ν
(
)
r
centred at each
atom location in a supercell containing the QD and its surrounding matrix,
∑
αα α,,
()
nn
vr d
.
Here, α denotes the atom type and
d
n
α,
its equilibrium position, which was obtained by minimiz-
ing the strain energy [80] . Spin-orbit coupling is included as a similar sum of non-local poten-
tials [79] . EPM parameters fi tted to the bulk band structure parameters of GaSb and GaAs were
used [81] . For the type II QDs, the energy structure was evaluated by applying a novel self-
consistent mean fi eld (SCF) calculation to the multiple electron–hole pair excitations within the
EPM framework. The SCF Hamiltonian may then be written as:
2
()
() ()
2
2
m
Vr drdr
rr
rrr r
eh
∇+
∫
33
ρρ
ε()
(8.8)
where ρ
e
( ρ
h
) is the density of the occupied conduction band (unoccupied valence band) states,
excluding the state being calculated. The present approach treats the electron–electron and
electron–hole interactions at the Hartree–Fock level for the one exciton and two exciton ground
states.
Using a linear combination of bulk Bloch functions as the basis, the single particle energies
and orbitals were calculated for a few of the lowest conduction and highest valence band states
with zero, one, and two electron–hole pairs [82] .
The exciton and two exciton energies were calculated as the sum of single particle energies,
corrected for double counting of the Coulomb interaction. For example, the two exciton energy
E
XX
is given by:
EEEVV
XX e h e h
2( ) ( )
(8.9)
where E
e
and E
h
are the energies and V
e
and V
h
are the expectation values of the third term in
Eq. 8.8 for the lowest conduction band and highest valence band states, respectively. The two exciton
binding energy is given by 2 E
X
E
XX
. A negative binding energy indicates that the two exciton-
to-exciton emission in PL would appear on the higher energy side of the exciton emission.
The calculated binding energy as a function of QD size is shown in Fig. 8.22 . This result cor-
responds to typical self-assembled GaSb QDs of heights in the range of 4.8 to 6.6 nm with the
CH008-I046325.indd 288CH008-I046325.indd 288 6/25/2008 2:30:11 PM6/25/2008 2:30:11 PM
