Henini M. Handbook of Self Assembled Semiconductor Nanostructures for Novel devices in Photonics and Electronics

Подождите немного. Документ загружается.

Growth and Characterization of ZnO Nano- and Microstuctures 299

(b)

Linear fit (range: 500–4000 pulses)

Y  A  B X

Aspect ratio

Parameter Value Error

A 8.001

0.003

1.104

2.781E-4B

1000 10000

Number of deposition pulses

3500

(a)

Number of PLD pulses

16000

8000

4000

2000

1000

3000

Whisker length (nm)

2500

2000

1500

1000

500

0204060

Whisker diameter (nm)

80 100 120

(d)

0 20 40 60 80 100 120 140 160

100

Number of PLD pulses

16000

8000

4000

2000

Distribution function (%)

Whisker diameter (nm)

(c)

Counts

10 20 30 40 50 60

Whisker diameter (nm)

Figure 9.3 Detailed growth evolution study of ZnO nanowires. (a), (b) Diameter, length and the aspect ratio

in dependence of the number of PLD pulses. The linear ﬁ t in (b) includes the data points up to 8000 laser pulses.

for different samples.

Mean value

bar: standard deviation

130

120

Whisker diameter (nm)

110

100

Substrate

Target

Plume

Relative position on sample (mm)

01234567 9810

Figure 9.4 Lateral homogeneity investigation over a sample. 1–5 represent different spots on the substrate, from

front edge (near plasma, spot 1) to the back edge (spot 5, see inset). The bar indicates the standard deviation from the

mean ZnO whisker diameter.

CH009-I046325.indd 299CH009-I046325.indd 299 6/24/2008 3:04:59 PM6/24/2008 3:04:59 PM

300 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

9.2.4 Structural characterization

XRD measurements show that the crystallographic c -axis of the ZnO nanowires is oriented per-

pendicular to the surface of the a -plane sapphire substrate. Figure 9.6 depicts an HRXRD diffracto-

gram of the ZnO(0002) and the Al

()1120

substrate reﬂ ection of the ZnO nanowire sample of

Figs 9.4 and 9.5 . The corresponding peak widths (FWHMs) are 22 arcsec and 15 arcsec, respec-

tively. This underlines the superior crystalline quality of the whiskers as compared to ZnO thin

ﬁ lms. The rocking curve of the ZnO (0002) reﬂ ection has an FWHM of 0.31° (inset of Fig. 9.6 )

which is comparable to the best values reported for ZnO nanowires and PLD thin ﬁ lms [10, 51, 86] .

Hence, as it can be seen already in the SEM pictures, there is very little tilt between the whiskers.

However, the crystal quality changes signiﬁ cantly with the growth temperature. In Fig. 9.7 the

peak width of the ZnO(0002) reﬂ ection is shown for the rocking curve as well as for the 2 θ – ω scan

Whisker length (nm)

4500

4000

3500

3000

2500

2000

Position on substrate

50 60 70 80 90

Whisker diameter (nm)

100 110 120 130 140 150

Figure 9.5 ZnO whisker length vs diameter for different positions on a single substrate. The positions 1–5 corre-

spond to the inset of Fig. 9.4 .

34.35 34.40

34.45 37.75 37.80

2θω ()

ZnO (0002)

FWHM  22”

ZnO (0002)

FWHM  0.31

Sapphire

(1120)

FWHM  15”

17 18

1, 000

100

Intensity (counts)

Omega ()

10 000

1000

100

Intensity (counts)

Figure 9.6 XRD diffractogram of a ZnO nanowire sample. The peak widths of the ZnO and the substrate reﬂ ection

are in the range of the instrumental line broadening (12 arcsec, determined with sapphire and Si substrates). The

rocking curve of the ZnO (0002) reﬂ ection with an FWHM of 0.31° is shown in the inset.

CH009-I046325.indd 300CH009-I046325.indd 300 6/24/2008 3:05:00 PM6/24/2008 3:05:00 PM

Growth and Characterization of ZnO Nano- and Microstuctures 301

1500

500 600 700

Temperature (C)

FWHM

2θ

(arcsec)

FWHM

(arcsec)

800 900

1250

1000

750

500

250

400350300250

Heater power (W)

200

150100

FWHM

200

175

150

125

100

Figure 9.7 FWHMs of the ZnO(0002) reﬂ ection (XRD) vs growth temperature; black: 2 θ – ω -scan width (left

axis), red: rocking curve width (right axis).

(a) (b) (c)

(011)

(001)

(010)

5nm

50 nm

200 nm

Figure 9.8 TEM images of a single ZnO nanowire. The inset in (a) shows the corresponding SAD pattern of the

whisker. In (b) the arrows indicate the positions of steps on the side faces which are shown in more detail in (c).

(b) and (c) were studied in the [100] zone axis.

in dependence of the heater power/temperature. Both widths are minimal for growth temperatures

between 850 and 900°C though it should be noted that this trend is more pronounced for the 2 θ – ω

scans than for the ω scans. The data points at 150 W heater power come from samples which were

grown on the bare substrate without employing any catalyst. Those samples are subject to ongoing

investigations. Preliminary results indicated that catalyst-free ZnO growth is possible by the low-

vacuum PLD set-up at sufﬁ ciently low temperature. The c -axis lattice constants for the pure ZnO

samples was 5.207 Å which is again exactly the value for bulk ZnO.

The typical rod-like growth morphology is studied in more detail by TEM ( Fig. 9.8 ). A single

crystalline wurtzite ZnO whisker with a little gold droplet on top is revealed. However, the diam-

eter of the whisker is much larger that the droplet size. The inset of Fig. 9.8a shows the SAD

of ZnO. As already deduced from the XRD measurements, the growth direction is parallel to the

c -axis of ZnO and in accordance with the very low FWHMs of the XRD ZnO(0002) reﬂ ection,

dislocations in the nanowires are very rare. Figure 9.8b and c depicts steps on the side surfaces of

the whiskers which are not periodic along the growth direction and not symmetric on both wire

CH009-I046325.indd 301CH009-I046325.indd 301 6/24/2008 3:05:01 PM6/24/2008 3:05:01 PM

302 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

sides. They exhibit various heights usually between 1 and 15 atomic steps. In Fig. 9.8c the impor-

tant ZnO planes as well as the step habit plane are indicated. Angled

{}1123

faces as reported in

[87] were not observed here.

9.3 Optical properties I: whispering gallery modes

9.3.1 Nanowire luminescence

Depending on the respective growth conditions the PLD process provides a variety of differently

shaped ZnO micro- and nanocrystals shown in Fig. 9.9 . The room temperature luminescence

of our PLD grown ZnO nanostructures typically consists of two bands, the ﬁ rst (UV) around

3.25 eV, the second (visible, VIS) around 2.35 eV. The UV band is associated with free-exciton

emission. The latter is also called “ green band ” in the literature; its exact nature, involving deep

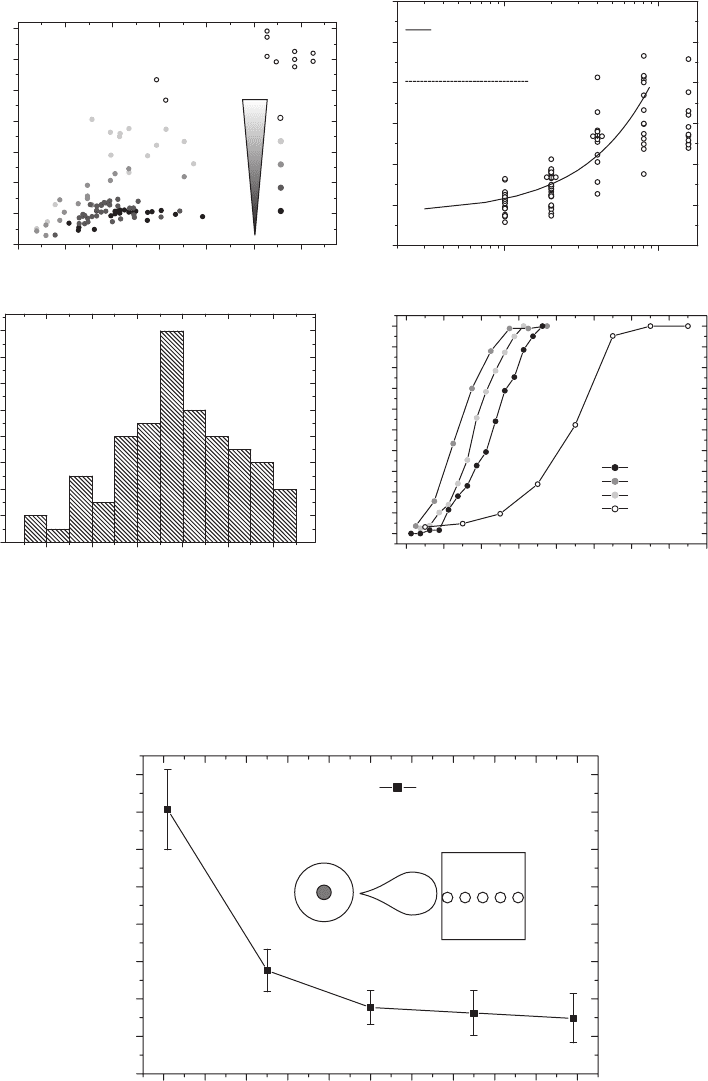
levels, is still under debate. Figure 9.10 shows typical CL spectra of arrays of ZnO nanowires

within the spectral region of donor-bound exciton (DBX) emission for T  10 K. The size of the

excited nanowire array has been increased from a few (1–3) wires up to 100–300 wires. All CL

spectra are dominated by a strong emission line at 3.360 eV indicating the recombination of

excitons bound to a neutral aluminium donor ( I

, [88] ). The FWHM of this line varies from 1.4

to 2.0 meV and is thus comparable to values for high-quality PLD-grown thin ﬁ lms and single

crystals [80, 89] . A transition at 3.364 eV possibly belongs to an ionized–donor bound exciton

( I

, [88] ). The luminescence intensity of further DBXs (3.356 eV, indium, I

[88] ) is weaker by

about one order of magnitude. Free-exiton (FX) emission is barely visible at this temperature. The

absence of signiﬁ cant differences between the CL spectra originating from different array sizes

proves the lateral homogeneity of the nanowire sample on the μ m scale.

(a)

(c)

(b)

(d)

1 m

1 m3 m

0.3 m

Figure 9.9 Different shapes of PLD grown ZnO micro- and nanocrystals. (a) Hexagonal microcrystals with

diameters of about 2 μ m. (b) ZnO nanowires with diameters around 100 nm. (c) Needle-like nanostructures.

(d) Microcrystals exhibiting a dodecagonal cross-section.

CH009-I046325.indd 302CH009-I046325.indd 302 6/24/2008 3:05:13 PM6/24/2008 3:05:13 PM

Growth and Characterization of ZnO Nano- and Microstuctures 303

CL intensity (arb. log. units)

3.353.34 3.36 3.37 3.38

Photon energy (eV)

~10

~100

Number

of wires

DBX FX

FWHM

1.4–2.0 meV

T  10 K

Figure 9.10 CL spectra (shifted vertically for clarity) of arrays of ZnO nanowires within the spectral region of donor-

bound exciton (DBX) emission. The excited lateral area of the nanowire sample has been increased to include 1–3

nanowires (lower curve), 10–30 nanowires (middle curve) and 100–300 nanowires (upper curve). Vertical lines refer

to dominating DBX transitions. The dashed vertical line marks the expected position of free exciton (FX) emission.

3.30 3.32 3.34 3.36 3.38

10 K

30 K

50 K

70 K

90 K

120 K

150 K

Photon energy (eV)

CL intensity (arb. log. units)

DBX

3.20 3.25 3.30 3.35 3.40

Photon ener

y (eV)

10 K

30 K

50 K

70 K

90 K

DBX 1LO

DBX 2LO

TES

FX 1LO

FX 2LO

(b)

(a)

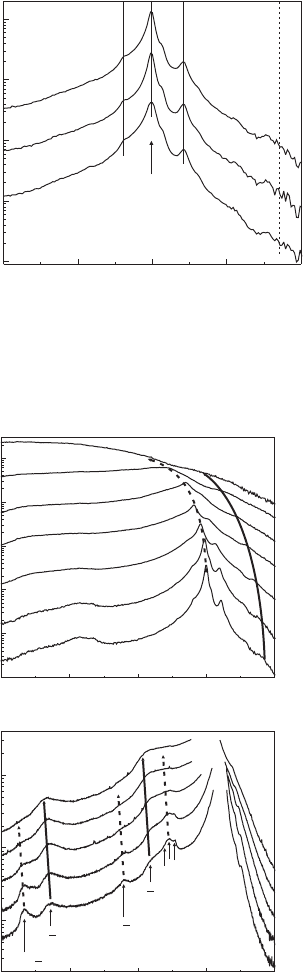
Figure 9.11 Temperature dependence of CL spectra of an array of about 10 nanowires. Results are given for the

spectral region of DBX emission (a) and for the spectral region of phonon replica (b).

With increasing temperature ( Fig. 9.11 ) all transitions broaden and shift to lower energies.

DBX emission vanishes (dashed line in Fig. 9.11a ), while FX emission gains in intensity (solid

line). Figure 9.11b focuses on photon energies  3.34 eV. Phonon replicas and two electron satel-

lites (TES) of the DBX lines can be observed [88] . Both types of transitions vanish with increasing

CH009-I046325.indd 303CH009-I046325.indd 303 6/24/2008 3:05:17 PM6/24/2008 3:05:17 PM

304 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

temperature (dashed lines) due to their physical correlation to donor bound excitons. Additional

peaks that can be detected even at elevated temperatures indicate phonon replicas of the FX tran-

sition (solid line). Due to the relative large diameter of ZnO wires presented here, a quantum con-

ﬁ nement effect is neither expected nor visible in the spectra.

2.6 2.8

2.42.2

Photon energy (eV)

CL intensity (arb. units)

TM polarization

2.01.8

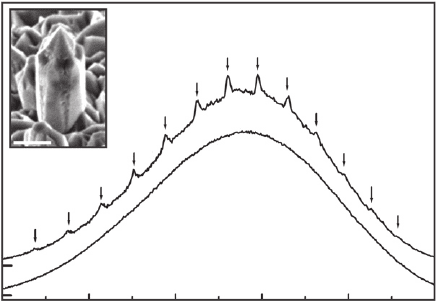
Figure 9.12 Room temperature VIS emission CL spectra of a ZnO microcrystal (curve 1) and of thin ﬁ lm material

(curve 2) scaled to the same intensity and vertically shifted for clarity. Arrows mark theoretical energetic positions

of WGMs due to Eq. 9.1 for TM polarization and D  2.86 μ m. The inset shows an SEM image of the investigated

microcrystal. The scalebar has a length of 2 μ m. The experimental cavity diameter is D

exp

 (2.90  0.06) μ m.

Figure 9.12 shows the typical VIS emission CL spectrum from a ZnO microcrystal. An electron

microscopy image of the crystal is given in the inset. In comparison to the broad and unstruc-

tured VIS emission of thin ﬁ lms or bulk material, VIS emission of the microcrystal is accompa-

nied by a series of comparatively sharp peaks. This modulated broad band is visible and can be

assigned to optical whispering gallery resonances. Within the VIS range ZnO is optically trans-

parent and exhibits a refractive index of n ⬇ 2 [90] , i.e. ZnO micro- and nanocrystals represent

(hexagonal) dielectric resonators in a wide spectral range.

9.3.2 Theory of hexagonal whispering gallery modes

9.3.2.1 Dielectric resonators

From a general point of view a dielectric resonator is a transparent body of certain shape con-

sisting of a substance with a high refractive index n , usually surrounded by air. Such a struc-

ture has the ability to conﬁ ne light inside, e.g. utilized in any kind of optical ﬁ bres or waveguides.

To explain this phenomenon in terms of classical electrodynamics, and any similar problem

respectively, it is necessary to solve the three-dimensional wave equation for the given geometry.

Steady-state solutions of this equation are then usually called eigenmodes of the considered

resonator.

In the case of a hollow metallic resonator as an example for a so-called closed cavity, a discrete

set of eigenmodes exists related to a discrete spectrum of eigenmode energies [91] . This is due to

the boundary conditions for the electric and magnetic ﬁ eld that lead to a complete suppression of

wave propagation outside the resonator. Hence, no energy is radiated from the hollow resonator;

the whole radiation ﬁ eld is restricted inside the metallic cavity.

In contrary, a dielectric resonator is an open cavity. Because of the continuity conditions for the

electric and magnetic ﬁ eld at the cavity’s boundary, the radiation ﬁ eld is not exclusively restricted

to the resonator itself, but actually extended to inﬁ nity. This results in a permanent radiation loss

of energy and, hence, every imaginable ﬁ eld distribution decays exponentially with a lifetime τ ,

therefore not representing a steady-state solution [92] . The actual solutions of this problem form

a continuum of so-called scattering states consisting of an incoming plane wave and an outgoing

CH009-I046325.indd 304CH009-I046325.indd 304 6/24/2008 3:05:17 PM6/24/2008 3:05:17 PM

Growth and Characterization of ZnO Nano- and Microstuctures 305

scattered wave. Therefore, the eigenmodes of a dielectric cavity appear as maxima within the

continuous spectrum of the total scattering cross-section in dependence of the energy of the

incoming wave. Those maxima, i.e. those incoming wave energies that exhibit the strongest

interaction with the given resonator, are usually called resonance energies or resonances of the

dielectric cavity [92] . Due to the above-mentioned ﬁ nite lifetime, all resonances exhibit a ﬁ nite

linewidth. The larger the losses of a given resonance the shorter is the lifetime and the larger is

the resonance’s linewidth.

9.3.2.2 Two-dimensional hexagonal resonator

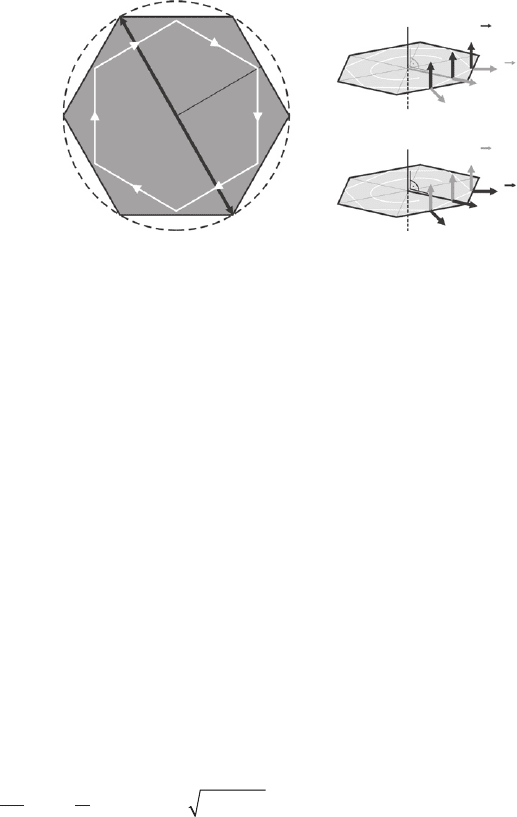
An important class of dielectric resonators are two-dimensional cavities, i.e. their in-plane

dimensions are much larger compared to their height. In this case, wave propagation parallel to

the longitudinal axis c is negligible. The light can be assumed to circulate around only within the

resonator’s cross-section. The respective mode patterns are so-called whispering gallery modes

(WGMs), obtained by solving the wave equation in its two-dimensional form. Hence, two decou-

pled types of polarizations occur [92] , namely TE polarized modes ( E ⬜ c ), and TM polarized

modes

()E||c

as explained in Fig. 9.13b and c .

TE mode

TM mode

(c)

(b)

(a)

Figure 9.13 (a) The light conﬁ ned within a hexagonal cross-section can be assumed to circulate inside the cavity

as indicated by the white arrows. The geometry of the cavity can be described by the radius of the incircle R

, by the

radius of the circumscribing circle R , or by its related diameter D  2 R using the geometric relation R  2 R

/ 兹 3.

Note that the circumference of the inscribed white hexagon has a length of 6 R

. (b), (c) Two possible types of polari-

zation of two-dimensional whispering gallery modes, exemplarily given for a hexagonal resonator. For TE modes the

electric ﬁ eld is transverse to the longitudinal axis of the resonator, for TM modes the magnetic ﬁ eld is.

Eigenmodes of such two-dimensional whispering gallery resonators have been calculated in

the past; the solutions for a circular cavity can be expressed in an analytical way [93] . Other

kinds of geometries have been subject to present literature, as, e.g., deformed circles [94, 95] ,

rectangles [96] or hexagons [97] , which necessarily have to be calculated numerically [97, 98] .

A scheme of the geometry of the two-dimensional hexagonal cavity is given in Fig. 9.13a .

The results of theoretical modelling [97] show that the eigenmodes of such a hexagonal cav-

ity can be numbered by an integer mode number N . Additionally, the modes can be distinguished

concerning their symmetry, e.g. leading to pairs of degenerated modes N



and N



related to their

respective chirality. In [16] , hexagonal WGMs have been calculated for a ﬁ xed n  1.466 and in

the mode number range of about N  20 to 70.

For large mode numbers N  70 a simple plane wave model (PWM) has been deduced [97] . Its

main idea is that the light wave circulates around exploiting the process of multiple total internal

reﬂ ection (TIR, see Fig. 9.13a ) and ﬁ nally interferes with itself when having completed one full cir-

culation within the resonator. To enforce constructive interference the total phase shift of the wave

along its path has to be an integer multiple of 2 π , i.e. only entire wave trains are allowed to perform

multiple circulations generating a standing wave. Taking into account the polarization-dependent

negative phase shift that occurs during the process of TIR [91] , we obtain the following equation:

arctan 

()

⎡

⎣

⎢

⎤

⎦

⎥

(9.1)

CH009-I046325.indd 305CH009-I046325.indd 305 6/24/2008 3:05:18 PM6/24/2008 3:05:18 PM

306 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

The factor β is polarization; for TM polarization β  β

™

 n

 1

has to be used; TE polarization

leads to β  β

 n . Due to the spectral dependence of the refractive index n  n ( E ), Eq. 9.1

is an implicit equation to determine the discrete resonance energies E  E

( R

) in terms of the

geometric parameter R

, Planck’s constant h and vacuum speed of light c . The ﬁ rst factor of the

right side of Eq. 9.1 corresponds to the wavelength in matter. The integer N  1 characterizes

the interference order of the resonance, which is in this case identical to the respective WGM

number [97] . The following term containing β refers to the additional phase shift mentioned

above. Furthermore, since ZnO is uniaxial,

nn

( E ) and n  n

⬜

( E ) have to be applied for TM and

TE polarization, respectively. We note that Eq. 9.1 for TM polarisation and n  const. is identical

to Eq. (17) of [16] . Neglecting the spectral dependency of n , Eq. 9.1 leads to:

∝

(9.2)

and thus WGMs generally shift to higher energies with decreasing cavity diameter. Note that

although TIR suggests that it is not possible for the light to leave the resonator, emission never-

theless occurs at the corners of the hexagon [97] . After all, radiation losses are always allowed

due to the reasons given in Section 9.3.2.1. Therefore it is possible to optically detect WGMs.

Since the geometrical model leading to Eq. 9.1 is a combination of basic ray and plane wave

optics, it is expected to be valid only for R   λ , i.e. for N   1 [97] . However, we show in this

work that Eq. 9.1 describes the experimentally found WGMs even down to mode number N  1 .

9.3.3 Whispering gallery modes in hexagonal ZnO microcrystals

Using the PWM, those peaks in Fig. 9.12 can unambiguously be attributed to WGMs of a hex-

agonal cavity. Therefore it is necessary to determine the correct mode number N of every sin-

gle detected peak. Provided that this mode number is known, Eq. 9.1 enables one to calculate

the theoretical diameter of the crystal D  4 R

/ 兹 3 out of every single detected peak energy.

Fortunately, since the peaks have to be numbered in ascending order, one only has to ﬁ nd the

correct mode number to start. The best ﬁ tting and therefore the ﬁ nal peak numbering is found if

every single peak predicts the same radius as all the other resonance peaks, or at least if the vari-

ations in the predicted radius become smallest. This procedure is explained in more detailed in

Fig. 9.14 .

For the investigated crystal, the correct mode numbering is shown also in Fig. 9.3 ; the respec-

tive theoretical diameter yields to D

theory

 2.86 μ m with a small minimum–maximum spreading

of less than 10 nm. Although theory predicts both TM and TE polarization, all calculations have

been performed for TM type, since polarization-dependent microphotoluminescence experiments

showed that WGMs are preferentially TM polarized (see Fig. 9.7 ). The required data for

()

were

obtained from ellipsometry measurements on PLD-grown ZnO thin ﬁ lm samples [90] .

The experimentally determined cavity diameter obtained from electron microscopy amounts to

exp

 (2.90  0.06) μ m. Hence, the deviations between theory and experiment are in the range

of only 2%! This means that the simple PWM ﬁ ts very well, even if N is in the range of only 20 to

30. To emphasize this fact, the theoretical values E

calculated for ﬁ xed diameter D  D

theory

are

given as black arrows in Fig. 9.3 ; they appear very close to the measured peaks. We note that if

a constant value of the index of refraction n without spectral dispersion is used, the agreement

between theory and experiment becomes worse.

9.3.4 Whispering gallery modes in ZnO nanostructures

Although the simple PWM obviously is valid for WGMs with mode numbers in the range of

about N  20–30, i.e. for optical cavities in the micrometre regime, it does not necessarily need

to be valid for nanostructures. Furthermore, prism-shaped microcrystals only enable analysis of

WGMs for ﬁ xed cavity diameter given by the cross-section of the particular microcolumn. Those

restrictions can be vanquished by focusing on nanostructures with a needle-like shape.

CH009-I046325.indd 306CH009-I046325.indd 306 6/24/2008 3:05:18 PM6/24/2008 3:05:18 PM

Growth and Characterization of ZnO Nano- and Microstuctures 307

9.3.4.1 ZnO nanoneedles

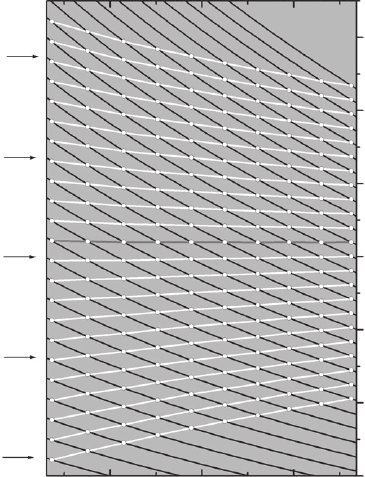
An example of an array of PLD-grown ZnO nanoneedles is shown in Fig. 9.15a . As can be seen

in Fig. 9.15b–d , the width of the hexagonal cross-section of a selected needle is continuously

tapered when approaching the needle’s top. Since the aspect ratio of this structure is very high,

every plane perpendicular to the needle’s longitudinal axis creates a hexagonal cavity and actu-

ally those structures allow for systematic investigations of WGMs in the nanometre regime from

D  800 nm down to D  0 !

9.3.4.2 Detection

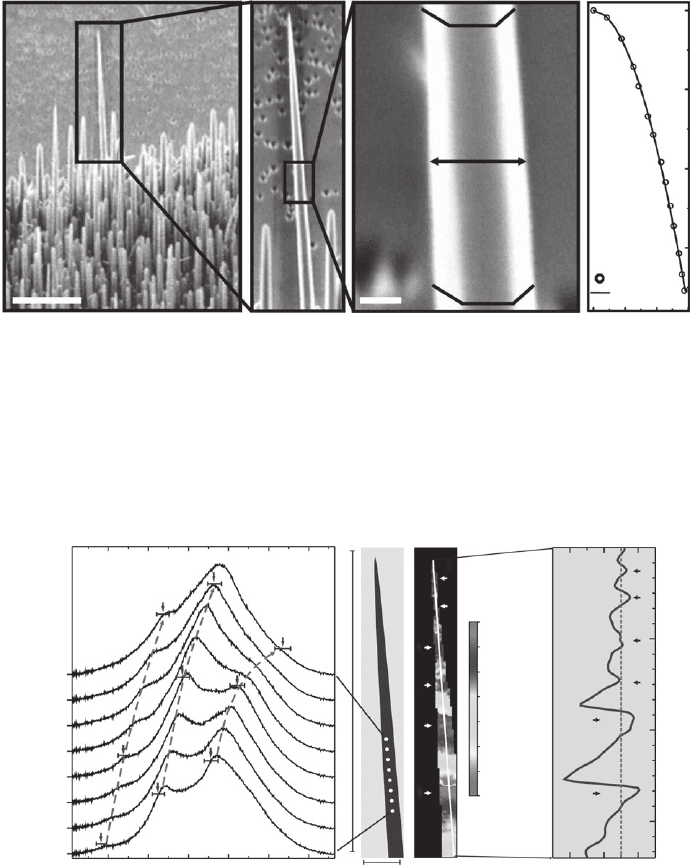
For this purpose, we performed spatially resolved CL experiments [99, 100] , i.e. pointwise CL

spectra have been recorded across the whole needle using a scan grid of 16  150 points. Typical

spectra and their interpretation are given in Fig. 9.16 . As in the case of microcrystals, the broad

VIS band of luminescence again is modulated due to a preferred constructive interference of

light whose photon energy again fulﬁ ls the resonance condition of Eq. 9.1. For decreasing diam-

eter, approaching the top of the needle, these maxima continuously shift to higher energies. This

effect supplies the unambiguous proof that the measured spectral modulation actually originates

from WGMs. When the dominating WGM with number N is blue shifted so far that it leaves the

VIS range, the next lower resonance N  1 occurs at lower energies indicated by a discontinu-

ous red shift of the spectral maximum in Fig. 9.16c and d . This process continues until N  1 i s

reached referring to the last resonance that can be observed.

1.8

Resonance

number

N  30

N  25

 21

 1.24 m

N  20

N  15

N  10

1.6

1.4

1.2

Incircle radius (m)

1.0

0.8

0.6

2.0 2.2 2.4

Resonance ener

y (eV)

Figure 9.14 Diagram R

( E ) to determine the correct mode numbering for the spectrum of Fig. 9.12. Equation 9.1

enables one to calculate the radius of the cavity incircle R

 R

( E , N ) out of a given resonance number N and resonance

energy E . The resulting set of curves is given here for N  10 … 41 as a set of black lines approximately exhibiting a

hyperbolic shape (as expected from Eq. 9.2). The index of the curves, i.e. the respective resonance number, is shown on

the left side of the scheme marked by black arrows. The experimentally detected resonance energies are given as white

circles. Since the resonances have to be numbered in ascending order, every white line represents a possible peak num-

bering. As can be seen from the diagram there exists only one peak numbering that results in an energy-independent

incirlce radius, denoted by the horizontal line. Hence, the starting number for the peak numbering of the spectrum in

Fig. 9.3 yields to N

 21 with R

 1 . 2 4 μ m; this leads to a respective cavity diameter D  2 . 8 6 μ m.

CH009-I046325.indd 307CH009-I046325.indd 307 6/24/2008 3:05:18 PM6/24/2008 3:05:18 PM

308 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

(d)(c)(b)(a)

Scan position x (µm)

Exp. data

Fit

D (nm)

300 600 900

Figure 9.15 SEM image of the investigated nanoneedle. All images have been obtained at 45° perspective. (a) SEM

image of an array of ZnO nanoneedles containing the reported one marked by a black rectangle. The scalebar has a

length of 10 μ m. (b) Larger-scale SEM image of the investigated nanoneedle. The needle’s diameter is continuously

tapered approaching zero at the top. (c) High-resolution SEM image indicating the hexagonal cross-section of the

needle. The scalebar has a length of 300 nm.(d) Experimentally determined shape of the needle. The obtained char-

acteristic of the diameter D vs scan position x can be ﬁ tted using a potential law D  x

0.523  0.007

, leading to a square

root-like shape of the needle.

Figure 9.16 Spatially resolved CL investigation of a single tapered ZnO nanoneedle. (a) CL spectra shifted vertically

for clarity collected at eight equidistant locations marked on the needle’s longitudinal axis by white dots in (b). The VIS

band of ZnO is modulated such that maxima can clearly be distinguished from each other and attributed to WGMs

labelled according to Eq. 9.1. Since the radius of the needle decreases along the longitudinal axis, the spectral maxima

continuously shift to higher energies as indicated by the red dashed lines. Blue arrows and error bars mark selected TM

resonance energies obtained from Eq. 9.1 and their error. (b) Experimentally determined shape of the needle. (c) Map

of the energy of the spectral maximum within the visible spectral range. (d) Line scan along the white line shown in (c).

The red dashed line gives the maximum position of the unstructured VIS band in bulk material.

1.8 2.0 2.2 2.3 2.6 2.8

CL intensity (arb. units)

17 m

Photon energy (eV)

2µm

N  5

N  6

2.2 2.3 2.4

Maximum energy (eV)

2.425

2.386

Resonance energy (eV)

Scan position x (µm)

2.346

2.309

2.272

2.237

2.202

2.168

(a) (b) (c) (d)

N  4

9.3.4.3 Polarization

To obtain essential information about the state of polarization of the detected WGMs we per-

formed local polarization-dependent microphotoluminescence experiments. These show that the

WGMs are preferentially TM polarized, since detecting TE polarization causes an almost complete

CH009-I046325.indd 308CH009-I046325.indd 308 6/24/2008 3:05:19 PM6/24/2008 3:05:19 PM