Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

934 Reinhold Haberlandt

Fig. 23.12. Comparison of D with rigid and vibrating lattice (left: set A; right:

set B)

Inﬂuence of Cations on D

The dynamics of even small neutral molecules with saturated bindings is

strongly inﬂuenced by the presence of exchangeable cations [44, 46]. This is

investigated for the NaCaA zeolite with 4 Na

and 4 Ca

ions. In this case

the windows – marked by w in Fig. 23.5 (right) – are (as in the case of the

cation-free LTA) free from cations. The unexpected (see [20]) strong eﬀect can

clearly be seen in Fig. 23.13 (left) and has been conﬁrmed experimentally,

meanwhile ([105], see Chap. 10). In comparison with the cation-free LTA,

the self-diﬀusivity decreases by up to two orders of magnitude. It should

be noted that the computational eﬀort is much larger in this case than in

the simulations for the cation-free form since much longer trajectories (up

to 5-10 ns) are necessary to evaluate such small diﬀusivities. Additionally,

the calculation of the forces resulting from the polarization energy is very

024 68

2.0

1.5

1.0

0.5

Fig. 23.13. Calculated diﬀusion coeﬃcients compared with NMR data (left: D of

methane in NaCaA and cation-free LTA; right: mixture of CH

/Xe in silicalite at

a total loading of 8 guest molecules per unit cell. The ratio of Xe/CH

content is

varied keeping the sum of concentrations constant.)

23 Statistical Theory and Molecular Dynamics of Diﬀusion in Zeolites 935

time-consuming although the full Ewald sum can be replaced by a corrected

r space part of this sum.

Comparison between MD Simulations and Experimental NMR

Data

Fig. 23.13 (left) shows MD results for diﬀerent situations. Comparison with

experimental results from NMR measurements [106] yields satisfactory agree-

ment in the case of set A.

Fig. 23.13 (right) shows that the agreement between numerical MD values

and measured NMR data is suﬃcient also in the case of methane and xenon

mixtures (for more details, see [107,108]).

Propagators and Related Functions

So-called propagators P (r,t|r

, 0 ) (see p. 928 and (23.22)) represent an-

other way to describe diﬀusion processes.

Experimentally accessible is the averaged propagator

P (r,t)=



p (r

) P (r

+ r,t|r

, 0) dr

, (23.25)

where p (r

) denotes the probability density of ﬁnding a molecule at posi-

tion r

. The averaged propagator represents the probability distribution of

molecular displacements r during the time interval t for an arbitrarily se-

lected molecule within the sample under study. The pulsed ﬁeld gradient

(PFG NMR) technique [82] allows the determination of the averaged prop-

agator [83, 84] over time and space scales of typically milliseconds and mi-

crometers. As an example, Fig. 10.1 of Chap. 10 displays the propagation

patterns of ethane in beds of zeolite NaCaA with two diﬀerent crystallite

sizes for diﬀerent temperatures [83].

In statistical physics and quasielastic neutron scattering (QENS) – with

the relevant time and space scales of 1...100 ps and nanometers –, the averaged

propagator P (r,t) is generally referred to as the self-part G

(r,t)oftheVan

Hove autocorrelation function G(r,t) [40,54–58]

G(r,t)=



j=1



=1

δ[r + r



(0) − r

(t)]

, (23.26)

with N denoting the particle number. This is seen to be the probability

density of ﬁnding some particle at time t at distance r from the position of

aparticleattimet

= 0. For distinguishable particles one can split G(r,t)

into the self-part G

and the distinct-part G

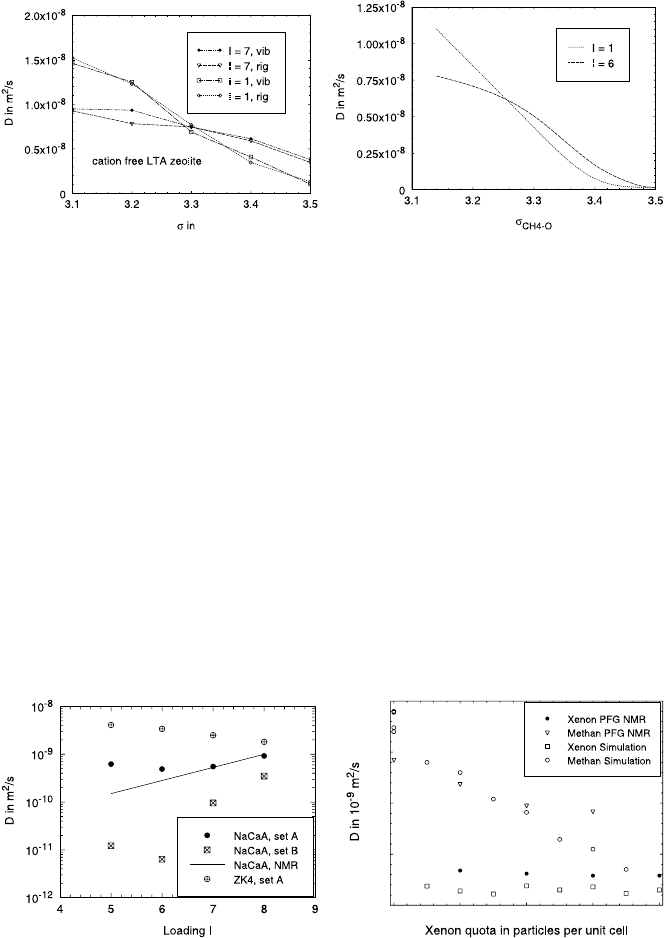
936 Reinhold Haberlandt

Fig. 23.14. Propagator P (r,t) as function of r and t; left: in ideal bulk systems;

right: in ‘ZK4’ (set B, I =3,T = 300 K).

G(r,t)=G

(r,t)+G

(r,t), (23.27)

(r,t)=



j=1

δ[r + r

(0) − r

(t)]

, (23.28)

(r,t)=



j=1



=1(=j)

δ[r + r



(0) − r

(t)]

. (23.29)

The self-part G

correlates positions of the same particle (j = ) at diﬀerent

times while G

correlates positions of diﬀerent ones (j = ). G

(r,t)givesthe

probability density that within time t a particle moves by r, while G

(r,t)

gives the probability density of ﬁnding a particle at time t at a distance r

from the position of another particle at time 0.

In a homogeneous system, the propagator P (r,t) (cf. (23.25)) is easily

found to have a Gaussian form

P (r,t)=(4πDt)

−

exp



−r

/ (4Dt)



, (23.30)

with D denoting the self-diﬀusivity.

The evolution of the probability of particle displacements as contained in

the spatial-temporal dependence of the propagator, corresponding to (23.30),

is shown in Fig. 23.14 (left). Fig. 23.14 (right) illustrates that the heterogene-

ity of the host system leads to a ﬁne-structure of the propagator – with spac-

ings given by the separation between adjacent pore centres. The propagator

in Fig. 23.14 (right) has been determined by MD simulations for methane in a

cation-free A-type zeolite (ZK4) for potential set B (see Table 23.2), loading

I = 3 and temperature T = 300 K [54, 55].

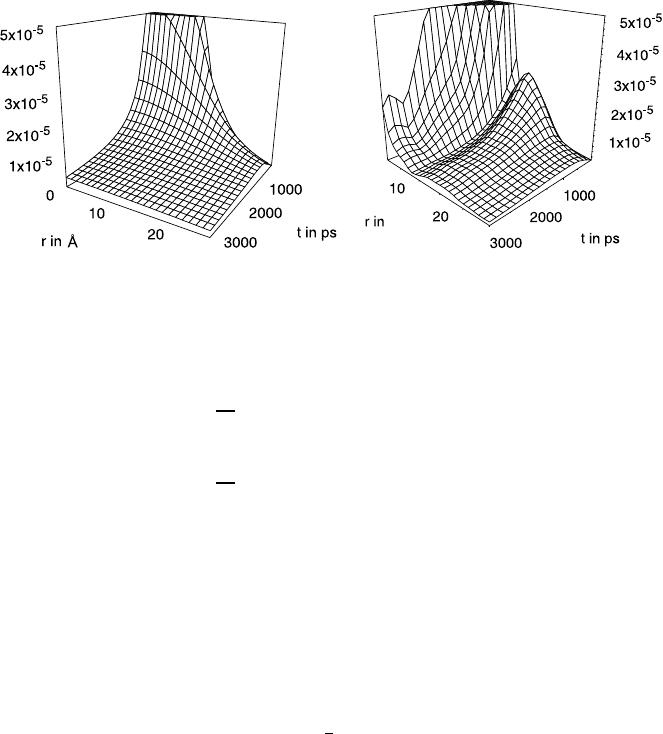
Fig. 23.15 shows – in another representation – the same behaviour for the

Van Hove function G

(x, t), Gaussian in the free space (above) and structured

for methane in ZK4 at I =3andT = 300 K (below). The speciﬁc structur-

ization of the propagators (see Figs. 23.14 (right) and 23.19) is caused by the

23 Statistical Theory and Molecular Dynamics of Diﬀusion in Zeolites 937

x in Å

t in ps

Gxt(,)

t in ps

x in Å

Gxt(,)

Fig. 23.15. Self-part G

(x, t) of the Van Hove correlation function in the bulk

(above) and the diﬀusion of methane in ZK4 at I =3andT = 300 K (below).

reﬂections of the guest molecules at the walls of the cavities in the zeolites

which yield peaks in the correlation functions. For an ideal zeolite lattice, the

periodicity of the propagator is conserved over arbitrarily large space and

time scales. This is demonstrated by Fig. 23.15.

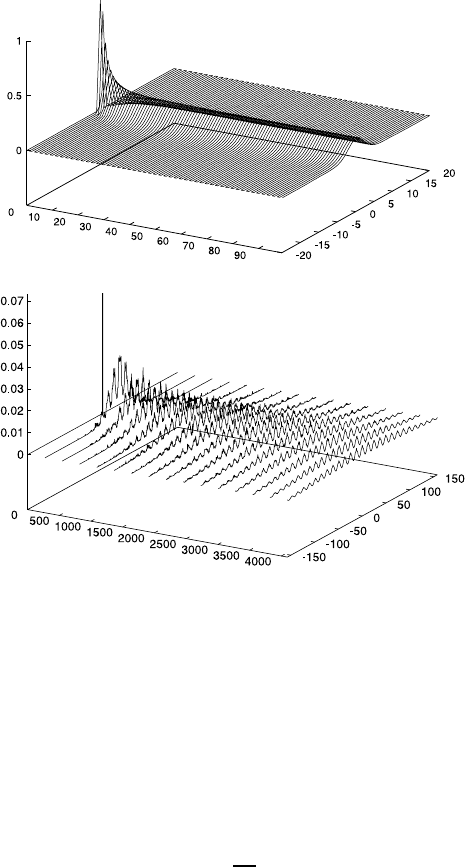
Figure 23.16 shows the dynamic structure factor S(k,ω)(k – wave vector,

ω – frequency), i. e. the double Fourier transform of the propagator (self-part

of the Van Hove function)

S(k,ω)=

2π



∞

−∞



P (r,t)e

−i(k·r−ωt)

dr dt (23.31)

as the quantity directly accessible by QENS [52, 53] (see Chaps. 2 and 3).

S(k,ω) is a generalization of the static case in which the diﬀerential cross

section is expressed in terms of the pair distribution function (see (23.7d)).

Fig. 23.17 shows the intermediate scattering function F (k,t)ofQENS,

whichisdeﬁnedby

F (k,t)=



P (r,t) e

−i kr

d r ,G

(r,t) ≡ P (r,t) (23.32)

938 Reinhold Haberlandt

k in Å

 in ps

Sk(, )

-1

Fig. 23.16. Self-part S

(k, ω) of the dynamic structure factor for methane in ZK4

at I =3andT = 300 K.

k in Å

t in ps

Fkt(,)

-1

Fig. 23.17. Self-part F

(k, t) of the scattering function for methane in ZK4 at

I =3andT = 300 K.

using the propagator of methane in cation-free zeolite LTA [54,55]. The scat-

tering vector k has been chosen to be parallel to one of the crystallographic

axes.

For zeolites of non-cubic structure, the propagator exhibits the diﬀer-

ences of molecular propagation in diﬀerent directions. This is exempliﬁed by

Fig. 23.18 showing the propagator with respect to the x-, y-andz-axes for

methane in silicalite.

The over-all self-diﬀusion coeﬃcient D evaluated from the corresponding

scattering factor S(k,ω)is8.6 ·10

−9

−1

, which is in good agreement with

the experimental value of 9.3 · 10

−9

−1

extrapolated from QENS data

measured by Jobic et al. [52]. Analytical approximations for G

(r,t)andthe

related quantities are given in [54,55]. The experimental observation of such

23 Statistical Theory and Molecular Dynamics of Diﬀusion in Zeolites 939

y in Å

t in ps

Gxt(,)

t in ps

x in Å

Gyt(,)

z in Å

t in ps

Gzt(,)

Fig. 23.18. Self-part G

of the Van Hove correlation function for the diﬀusion of

methane in silicalite in x-, y-, and z-direction at I =3andT = 300 K.

structured propagators is a challenging task for QENS. In the light of the

theory, such a behaviour should quite generally be expected.

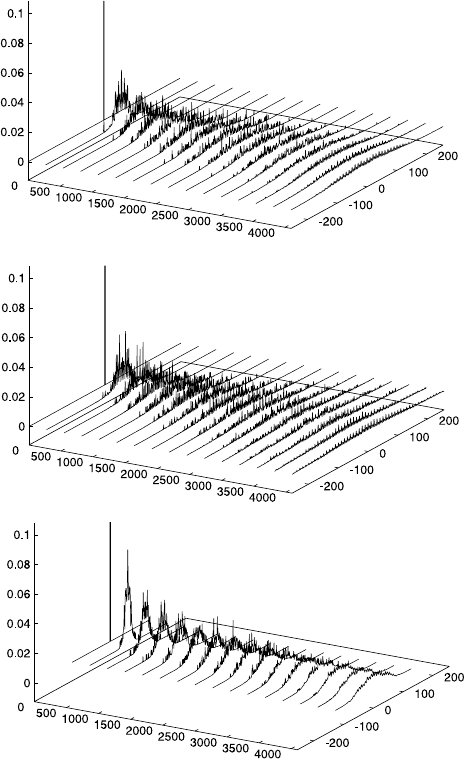
Fig. 23.19 uses an alternative representation of the propagator for vi-

sualizing the diﬀusion behaviour of C

in ZK4 in a time interval of

t =1....1000 ps [57,61]. In this case, the propagator was calculated with re-

spect to two coordinates x, y. It can be seen that the propagator shows a more

complicated structure than in the case of CH

, most likely as a consequence

of the more intricate intermolecular interaction.

940 Reinhold Haberlandt

0.02

0.04

0.06

0.08

0.10

P(x,y,t)

t=1 ps

0.005

0.010

0.015

0.020

P(x,y,t)

t=10 ps

0.003

0.006

0.009

0.012

P(x,y,t)

t=100 ps

0.002

0.004

0.006

P(x,y,t)

t=300 ps

0.001

0.002

0.003

P(x,y,t)

t=500 ps

0.0005

0.0010

0.0015

P(x,y,t)

t=1000 ps

Fig. 23.19. Two-dimensional graph of the time development of the propagator

P (x, y, t)(x, y in

A; t in ps) calculated from a trajectory (potential set A, see

Table 23.2, I =3,T = 300 K, D =2· 10

−9

−1

) [61].

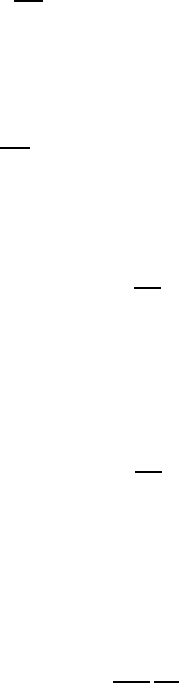
23 Statistical Theory and Molecular Dynamics of Diﬀusion in Zeolites 941

Transport-Diﬀusivity, Corrected Diﬀusivity and Self-Diﬀusivity

While the self-diﬀusion coeﬃcient D according to the Kubo theory may be

obtained from [2, 6, 17, 27, 48]

D =



j=1



∞

dtv

(0)v

(t), (23.33a)

the so-called corrected diﬀusion coeﬃcient D

includes the cross-correlations

between velocities of diﬀerent particles



j=1



k=1



∞

dtv

(0)v

(t). (23.33b)

The diﬀusion coeﬃcient that appears in Fick’s law is often called transport

diﬀusion coeﬃcient D

[14]

J = −D

d n

, (23.33c)

J is the ﬂux and n is the density. If the force F in the well-known relation

v = BF , (23.33d)

is substituted by the chemical potential µ one has

J = −nB

d µ

, (23.33e)

where B is the mobility. According to Kubo’s theory B is connected with the

corrected diﬀusivity by the relation

= Bk

T. (23.33f)

Comparison of (23.33c) and (23.33e) together with (23.33f) leads to

= D

dµ

, (23.33g)

which is a somewhat unusual form of the well-known Darken equation and has

been used already in Sect. 4.4 of Chap. 10 (cf. (10.23)) [14]. These diﬀerent

diﬀusivities obtained from equilibrium and non-equilibrium MD simulations

are compared with each other (Fig. 23.20 (right)). The self-diﬀusion coeﬃ-

cients have been obtained from the mean square displacement. D

results

from non-equilibrium simulations in which a density gradient (see Fig. 23.20

(left)) in six layers of cavities is created by randomly inserting particles that

leave the last layer and enter into the ﬁrst layer. The ﬂux has been evaluated

in the intermediate region only [48]. D

is obtained from the mean square

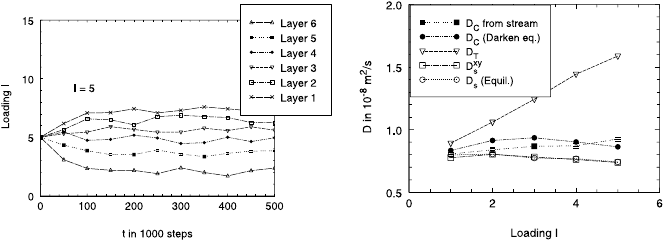
942 Reinhold Haberlandt

Fig. 23.20. Transport diﬀusion coeﬃcients (left: Concentration gradient versus

time; right: Transport diﬀusion coeﬃcient D

from non-equilibrium MD) in com-

parison to self-diﬀusion coeﬃcient D and corrected diﬀusion coeﬃcient D

displacement perpendicular to the density gradient. It turns out that the ﬂux

has practically no inﬂuence on the self-diﬀusion in the direction perpendic-

ular to the ﬂux. D

is somewhat larger than D, which might be attributed

to the collective eﬀects expressed by the cross-correlation terms in (23.33b).

is obtained from D

by the Darken equation and compared with results

from another non-equilibrium MD experiment. In this experiment, a ﬂux is

produced by an external ﬁeld. Measuring this ﬂux, D

may be obtained from

(23.33f).

23.5 Conclusion

Diﬀusion coeﬃcients of guest molecules in zeolites have been calculated under

diﬀerent conditions:

1. Statistical physics and molecular dynamics provide the basis for the eval-

uation of diﬀusion coeﬃcients of guest molecules in zeolites and for the

comparison to experimental data.

2. Summarizing this chapter one can state:

a) Even single particles diﬀusing through narrow cavities in zeolites show

a macroscopic behaviour, which obeys the diﬀusion equation for not

too small times and distances.

b) Temperature dependencies of diﬀusion coeﬃcients of guest molecules

show very often an Arrhenius behaviour.

c) Small changes in lattice parameters can cause dramatic changes in

the diﬀusion coeﬃcient, even in the dependence on concentration.

d) The presence of cations Na

,Ca

strongly inﬂuences the diﬀusion

of even neutral molecules [46], while the assumption of a ﬁxed lattice

seems to signiﬁcantly aﬀect the diﬀusion coeﬃcients only in excep-

tional cases. Thus, as a rule, a ﬁxed lattice can be used.

23 Statistical Theory and Molecular Dynamics of Diﬀusion in Zeolites 943

e) MD calculations for single- and two-component adsorbates are in fair

agreement with measured NMR and QENS data [22,53, 108].

f) Non-equilibrium simulations show that transport-diﬀusion includes

additional contributions in comparison with self-diﬀusion.

g) In order to get reliable data in evaluating the diﬀusion coeﬃcients

one needs good statistics, i. e. long runs with short time steps (up to

millions of steps of 5-10 fs each) and a large number of MD boxes

(here used up to 343).

h) Hierarchical simulations lead to an extension of the possible time

scale of the examined processes by orders of magnitude.

3. More information, especially about the analytical treatment of the diﬀu-

sion of guest molecules in zeolites (using for instance the Maxwell–Stefan

formulation (MS method) [26,85,86]), transition state theory (TST), dy-

namically corrected transition state theory (DCTST), lattice gas theories

and dynamical Monte Carlo simulations, respectively), can be found in

the literature [22, 90–104].

4. More and more the potentials used will be determined by diﬀerent meth-

ods such as ﬁtting procedures (i. e. comparison with experimental data)

and more sophisticated methods in determining intermolecular potentials

(i. e. quantum mechanical calculations and, later on, density functional

methods) [27,28, 67].

5. For the future, one can look forward to solving more complex and realistic

problems including diﬀusion and/or reaction – up to catalysis – of non-

reactive [107,108] and reactive mixtures of guest molecules. An overview

of a lot of recent examinations in the ﬁeld of diﬀusion and also some

simple models of chemical reactions and catalysis can be found in [22,23,

67, 109–123].

Notation

A

, A

ensemble, time average

D, D

(self-) diﬀusion coeﬃcient

corrected, transport diﬀusivity

force components

F (k,t) scattering function

f(ω) Fourier transform of



v(0) · v(t)



G(r, t) Van Hove auto correlation function

g(r) radial distribution function

H(q

,t) Hamiltonian function



(t)

(0)

transport coeﬃcient

ﬂux densities, generalized forces

(t) time correlation function A(t)B(0)

Boltzmann constant