Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors
Подождите немного. Документ загружается.


January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Appendix A: Field Quantization 429
and
[
ˆ
Π
l
(r,t),
ˆ
Π
j
(r
,t)]
±
=0 , (A.46)
where
[
ˆ
A,
ˆ
B]
+
=
ˆ
A
ˆ
B+
ˆ
B
ˆ
A (A.47)
and [
ˆ
A,
ˆ
B]
−
is given by Eq. (A.45). Both commutators occur in nature,
the minus commutator for Bosons like photons and phonons, and the plus-
commutator, usually called the anti-commutator, for Fermions, e.g., elec-
trons. By choosing the appropriate type of commutator, we automatically
get the correct quantized field theory.
i) photons
In the φ =0gauge, we have Π
i
(r, t)=(1/4πc
2
) ∂A
i
/∂t and A
i
(r,t) as
canonical variables. After quantization, the commutation relations are
[
ˆ
A
l
(r,t),
ˆ
Π
j
(r
,t)]
−
= iδ
lj
δ(r − r
) , (A.48)
and the Hamilton operator becomes
ˆ
H =
d
3
r
2πc
2
ˆ
Π
2
+
1
8π
( curl
ˆ
A)
2
. (A.49)
For many applications, we want to work in the Coulomb gauge
∇·A =0 , (A.50)
where the electromagnetic field is transverse. In this gauge, the commutator
between A and Π is no longer given by Eq. (A.48) because the individual
components of these operators are connected by ∇·A =0and ∇·Π=0.
In the Coulomb gauge, the commutator (A.48) has to be replaced by
[
ˆ
A
l
(r,t),
ˆ
Π
j
(r
,t)]
−
= iδ
t
lj
(r − r
) , (A.51)
see Schiff (1968). Here, the transverse δ-function is defined as
δ
t
lj
(r − r
)=δ
lj
δ(r − r
) −
1
4π
∂
∂r
l
∂
∂r
j
1
|r − r
|
. (A.52)
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
430 Quantum Theory of the Optical and Electronic Properties of Semiconductors
In order to introduce photon operators (in vacuum), we expand the field
operators in terms of plane waves
u
λk
=
e
ik·r
L
3/2
e
λk
, (A.53)
where e
λk
is the polarization unit vector, so that
d
3
ru
∗
λk
(r) · u
λ
k
(r)=δ
λλ
δ
k,k
(A.54)
and
λ=1,2
e
λk,l
e
λk,j
+
k
l
k
j
k
2
= δ
lj
. (A.55)
If we wanted to quantize the electromagnetic field in a resonator or in some
other geometry we would use the appropriate eigenmodes instead of plane
waves.
Since the electromagnetic field in the Coulomb gauge is transverse, we
know that k is perpendicular to e
λk
, implying that ∇·u =0. The expansion
of the field operators is
ˆ
A(r,t)=
k,λ
[
ˆ
b
λk
u
λk
(r)+
ˆ
b
†
λk
u
∗
λk
(r)]B
λk
(A.56)
and
ˆ
Π(r,t)=
1
4πc
2
∂
ˆ
A
∂t
=
k,λ
∂
ˆ
b
kλ
∂t
u
λk
+
∂
ˆ
b
†
kλ
∂t
u
∗
λk
B
λk
4πc
2
, (A.57)
where the expansion coefficients
ˆ
b,
ˆ
b
†
are the photon operators. We deter-
mine the quantity B
λk
so that the photon operators fulfill simple commu-
tation relations.
To evaluate the time derivative of the photon operators, we make use
of the fact that the vector potential A satisfies the wave equation
∂
2
∂t
2
− c
2
∇
2
ˆ
A =0 . (A.58)
Inserting the expansion (A.56), we obtain
∂
2
∂t
2
ˆ
b
λk
= −ω
2
k
ˆ
b
λk
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Appendix A: Field Quantization 431
and
∂
2
∂t
2
ˆ
b
†
λk
= −ω
2
k
ˆ
b
†
λk
, (A.59)
where ω
k
= ck. Equation (A.59) is fulfilled if
∂
∂t
ˆ
b
λk
= −iω
k
ˆ
b
λk
and
∂
∂t
ˆ
b
†
λk
= iω
k
ˆ
b
†
λk
. (A.60)
Inserting Eq. (A.60) into Eq. (A.57) yields
ˆ
Π(r,t)=−
1
4πc
2
iω
k
B
λk
(
ˆ
b
λk
u
λk
−
ˆ
b
†
λk
u
∗
λk
) . (A.61)
To determine the commutation relations of the photon operators, we insert
the expansions (A.56) and (A.61) into the commutator (A.48) to obtain
λ,k
λ
,k
−iB
λk
B
λ
k
ω
k
4πc
2
$
ˆ
b
λk
u
λk,l
(r)+
ˆ
b
†
λk
u
∗
λk,l
(r)
%
,
$
ˆ
b
λ
k
u
λ
k
,j
(r
) −
ˆ
b
†
λ
k
u
∗
λ
k
,j
(r)
%
= i δ
lj
δ(r − r
) . (A.62)
This commutator is satisfied if
[
ˆ
b
λk
,
ˆ
b
†
λ
k
]=δ
λλ
δ
kk
and
[
ˆ
b
λk
,
ˆ
b
λ
k
]=0=[
ˆ
b
†
λk
,
ˆ
b
†
λ
k
] (A.63)
and the normalization constant is chosen as
B
λk
=
2πc
2
ω
k
1/2
. (A.64)
Summarizing these results, we have
ˆ
A(r,t)=
λk
2πc
2
ω
k
ˆ
b
λk
u
λk
(r)+
ˆ
b
†
λk
u
∗
λk
(r)
, (A.65)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
432 Quantum Theory of the Optical and Electronic Properties of Semiconductors
ˆ
Π(r,t)=−i
λk
ω
k
8πc
2
ˆ
b
λk
u
λk
(r) −
ˆ
b
†
λk
u
∗
λk
(r)
, (A.66)
and the Hamiltonian
ˆ
H =
ω
k
2
(
ˆ
b
†
λk
ˆ
b
λk
+
ˆ
b
λk
ˆ
b
†
λk
)=
ω
k
(
ˆ
b
†
λk
ˆ
b
λk
+1/2) . (A.67)
ii) phonons
Here, we quantize the canonical variables into the field operators
ˆ
ξ
i
(r,t)
and
ˆ
Π
i
(r,t)=ρ∂
ˆ
ξ
i
/∂t with the commutations relations
[
ˆ
ξ
j
(r,t)
ˆ
Π
l
(r
,t)]
−
= iδ
jl
δ(r − r
) . (A.68)
Again, we expand the field operators
ˆ
ξ(r,t)=
[
ˆ
b
k
u
k
(r)+
ˆ
b
†
k
u
∗
k
(r)]B
k
(A.69)
and similarly for
ˆ
Π. Choosing the functions u as plane waves
u
k
(r)=e
k
e
ik·r
L
3/2
,
where e
k
= k/|k| and the normalization constant as B
k
=
/2ρω
k
,we
find the commutation relation between the phonon operators
[
ˆ
b
k
,
ˆ
b
†
k
]=δ
k,k
, (A.70)
and the Hamilton operator becomes
ˆ
H =
ω
k
(
ˆ
b
†
k
ˆ
b
k
+1/2) . (A.71)
iii) electrons
Here, we introduce the field operators
ˆ
ψ and
ˆ
Π=i
ˆ
ψ
†
and we use the
Fermi anti-commutation relations
[
ˆ
ψ,
ˆ
ψ]
+
=0=[
ˆ
ψ
†
,
ˆ
ψ
†
]
+
(A.72)
and
[
ˆ
ψ(r,t),
ˆ
Π(r
,t)]
+
= iδ(r − r
) , (A.73)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Appendix A: Field Quantization 433
which is equivalent to
[
ˆ
ψ(r,t),
ˆ
ψ
†
(r
,t)]
+
= δ(r − r
) . (A.74)
From the Hamilton density, Eq. (A.43), we obtain
ˆ
h =
1
i
ˆ
Π(r) H
sch
ˆ
ψ(r)=
ˆ
ψ
†
(r) H
sch
ˆ
ψ(r) , (A.75)
which yields the Hamilton operator of the noninteracting electron system
as
ˆ
H =
d
3
r
ˆ
ψ
†
(r) H
sch
ˆ
ψ(r) . (A.76)
The derivation of the Hamiltonian for an interacting electron system is
discussed, e.g., in the textbook of Davydov. Here, we only want to mention
that one has to start from the N-particle Schrödinger Hamiltonian which
is then transformed into the Fock representation. One finally obtains
ˆ
H =
d
3
r
ˆ
ψ
†
(r) H
sch
ˆ
ψ(r)
+
1
2
d
3
r
d
3
r
ˆ
ψ
†
(r)
ˆ
ψ
†
(r
) V (r, r
)
ˆ
ψ(r
)
ˆ
ψ(r) . (A.77)
This expression shows that the interaction term has a similar structure as
the single-particle term, but instead of H
sch
the electron density operator
ˆ
ψ
†
(r)
ˆ
ψ(r) times the potential V appears. The whole interaction term is
thus the product of the density operators at r and r
multiplied by the pair
interaction potential. The factor 1/2 appears to avoid double counting.
We now expand the field operators into the eigenfunctions φ
n
of the
single-particle Schrödinger Hamiltonian.
H
sch
φ
n
= E
n
φ
n
, (A.78)
so that
ˆ
ψ(r,t)=
ˆa
n
(t) φ
n
(r) . (A.79)
These eigenfunctions could be any complete set, such as the Bloch or Wan-
nier functions. It is important to choose the appropriate set for the problem
at hand. The electron operators obey the anti-commutation relation
[ˆa
m
, ˆa
†
n
]
+
= δ
n,m
, (A.80)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
434 Quantum Theory of the Optical and Electronic Properties of Semiconductors
and we obtain the single-particle Hamilton operator
ˆ
H =
n
E
n
ˆa
†
n
ˆa
n
. (A.81)
Similarly, from Eq. (A.77) we get the many-body Hamiltonian
ˆ
H =
n
E
n
ˆa
†
n
ˆa
n
+
1
2
V
m
n
mn
ˆa
†
m
ˆa
†
n
ˆa
m
ˆa
n
, (A.82)
where
V
m
n
mn
= m
n
|V |nm
is the matrix element of the interaction potential.
REFERENCES
Field quantization is treated in most quantum mechanics textbooks. See,
e.g.:
C. Cohen-Tannoudji, J. Dapont-Roc, and G. Grynberg, Photons and
Atoms, Wiley, New York (1989)
A.S. Davydov, Quantum Mechanics, Pergamon, New York (1965)
L.I. Schiff, Quantum Mechanics, McGraw-Hill, New York (1968)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Appendix B
Contour-Ordered Green’s Functions
In this appendix, we make the connection with the many-body techniques
which are appropriate to describe a nonequilibrium system on an advanced
level and which have been used in Chap. 21 to describe the quantum kinet-
ics in an interacting electron–hole plasma. We present a short introduction
to nonequilibrium Green’s functions and show that this formalism yields
quite naturally a method to determine the spectral and kinetic properties
of a many-body system, which is driven away from equilibrium by time-
dependent external fields. Naturally, we can only give a brief introduction
here, for further extensions we refer the reader to the existing literature.
We follow closely the introduction of the nonequilibrium functions by Haug
and Jauho (1996).
The nonequilibrium problem is formulated as follows. We consider a
system evolving under the Hamiltonian
H = h + H
(t) . (B.1)
The time-independent part of the Hamiltonian h is split in two parts: h =
H
0
+ H
i
,whereH
0
is a single-particle Hamiltonian and H
i
contains many-
body interactions. It is further assumed that the nonequilibrium part H
(t)
vanishes for times t<t
0
. (We will take t
0
→−∞at a suitable point.) The
nonequilibrium part is, in the context of the present book, the interaction
of the carriers with a laser pulse.
Before the perturbation is turned on, the system is described by the
thermal equilibrium density matrix,
R(h)=
exp(−βh)
tr[exp(−βh)]
. (B.2)
The task is to calculate the expectation value of a given observable, to
435
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
436 Quantum Theory of the Optical and Electronic Properties of Semiconductors
which one associates a quantum mechanical operator O,fortimest ≥ t
0
:
O(t) =tr[R(h)O
H
(t)] . (B.3)
The subscript H indicates that the dependence is governed by the full
Hamiltonian, i.e., O is written in the Heisenberg picture.
B.1 Interaction Representation
We transform the time-dependence of O
H
with the full Hamiltonian to a
simpler form, namely to that of O
h
with the stationary part of the Hamil-
tonian. To eliminate the time-dependent external perturbation, we use the
relation
O
H
(t)=v
†
h
(t, t
0
)O
h
(t)v
h
(t, t
0
) . (B.4)
Here,
v
h
(t, t
0
)=T {exp[−
i
t
t
0
dt
H
h
(t
)]} , (B.5)
the quantity H
h
(t) is the interaction representation of the time-dependent
perturbation H
(t)
H
h
(t)=exp[
i
h(t − t
0
)]H
(t)exp[−
i
h(t − t
0
)] , (B.6)
and T is the time-ordering operator which arranges the latest times to left.
We now introduce contour-ordered quantities. The expression (B.4) can
be written in another, but equivalent, form:
O
H
(t)=T
C
t
(
exp
−
i
C
t
dτH
h
(τ)
O
h
(t)
)
, (B.7)
where the contour C
t
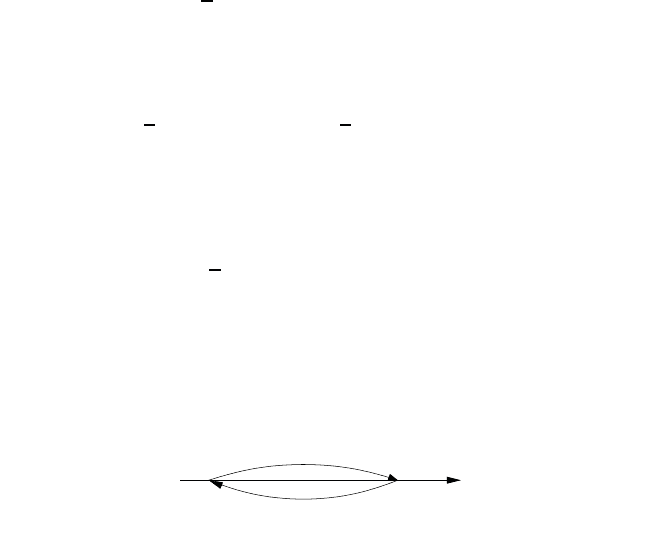
is depicted in Fig. B.1. Where possible, we employ the
convention that time variables defined on a complex contour are denoted
by Greek letters, while Roman letters are used for real time variables.
t
t
o
Fig. B.1 Contour C
t
.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Appendix B: Contour-Ordered Green’s Functions 437
The contour extends from t
0
to t and back again. Here, the time arguments
are on the real axis or slightly above it; if H
(t) can be analytically continued
no problems can arise. The meaning of the contour-ordering operator T
C
t
is the following: the operators with time labels that occur later on the
contour have to stand to the left of operators with earlier time labels. The
second part of the branch puts the exponential transformation operator to
the left of the operator O
h
(t). For a formal proof, we refer to Haug and
Jauho (1996). The contour-ordering operator is an important formal tool,
which allows us to develop the nonequilibrium theory along lines parallel
to the equilibrium theory.
We now define the contour-ordered Green’s function:
G(1, 1
) ≡−
i
T
C
[ψ
H
(1)ψ
†
H
(1
)] , (B.8)
where the contour C starts and ends at t
0
; it runs along the real axis and
passes through t
1
and t
1
once and just once (Fig. B.2).
tt
01
t
Fig. B.2 Contour C.
Here, ψ
H
and ψ
†
H
are the Fermion field operators in the Heisenberg picture.
Finally, we employ the shorthand notation (1) ≡ (Sx
1
,t
1
) [or (1) ≡ (Sx
1
,τ
1
),
when appropriate].
The contour-ordered Green’s function plays a similar role in non-
equilibrium theory as the causal Green’s function plays in equilibrium the-
ory: it possesses a perturbation expansion based on Wick’s theorem. How-
ever, since the time labels lie on the contour with two branches, one must
keep track of which branch is in question. With two time labels, which can
be located on either of the two branches of the contour of Fig. B.2, there
are four distinct possibilities. Thus, (B.8) contains four different functions:
G(1, 1
)=
G
c
(1, 1
)=G
++
(1, 1
) t
1
,t
1
∈ C
1
G
>
(1, 1
)=G
−+
(1, 1
) t
1
∈ C
2
,t
1
∈ C
1
G
<
(1, 1
)=−G
+−
(1, 1
) t
1
∈ C
1
,t
1
∈ C
2
G
˜c
(1, 1
)=−G
−−
(1, 1
) t
1
,t
1
∈ C
2
. (B.9)
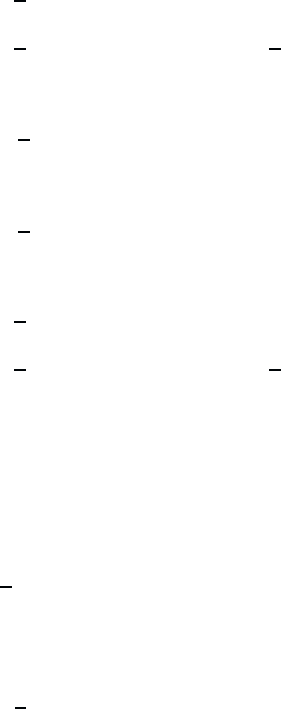
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
438 Quantum Theory of the Optical and Electronic Properties of Semiconductors
The notation with the contour time indices, which is used, e.g., in the book
by Schäfer and Wegener (2002), shows directly to which part of the contour
thetimeargumentbelongs.
In Eq. (B.9), we introduced the causal,ortime-ordered Green’s function
G
c
,
G
c
(1, 1
)=−
i
T [ψ
H
(1)ψ
†
H
(1
)] (B.10)
= −
i
θ(t
1
− t
1
)ψ
H
(1)ψ
†
H
(1
) +
i
θ(t
1
− t
1
)ψ
†
H
(1
)ψ
H
(1) ,
the “greater” function G
>
, also called hole propagator,
G
>
(1, 1
)=−
i
ψ
H
(1)ψ
†
H
(1
) , (B.11)
the “lesser” function G
<
, also called particle propagator,
G
<
(1, 1
)=+
i
ψ
†
H
(1
)ψ
H
(1) , (B.12)
and the antitime-ordered Green’s function G
˜c
,
G
˜c
(1, 1
)=−
i
˜
T [ψ
H
(1)ψ
†
H
(1
)] (B.13)
= −
i
θ(t
1
− t
1
)ψ
H
(1)ψ
†
H
(1
) +
i
θ(t
1
− t
1
)ψ
†
H
(1
)ψ
H
(1) .
Since G
c
+ G
˜c
= G
<
+ G
>
, there are only three linearly independent func-
tions. This freedom of choice is reflected in the literature, where a number
of different conventions can be found. For our purposes, the most suit-
able functions are G
>,<
(which are often also denoted by a common name,
“correlation function”), and the advanced and retarded functions defined as
G
a
(1, 1
)=
i
θ(t
1
− t
1
)[ψ
H
(1),ψ
†
H
(1
)]
+
= θ(t
1
− t
1
)[G
<
(1, 1
) − G
>
(1, 1
)] , (B.14)
and
G
r
(1, 1
)=−
i
θ(t
1
− t
1
)[ψ
H
(1),ψ
†
H
(1
)]
+
= θ(t
1
− t
1
)[G
>
(1, 1
) − G
<
(1, 1
)] . (B.15)
Obviously, G
a
(1, 1
)=G
r
(1
, 1)
∗
. We observe further that G
r
− G
a
=
G
>
−G
<
. Actually, the knowledge of two nonequilibrium Green’s functions
is sufficient to calculate all of them. Because of their different physical
