Harris C.M., Piersol A.G. Harris Shock and vibration handbook

Подождите немного. Документ загружается.

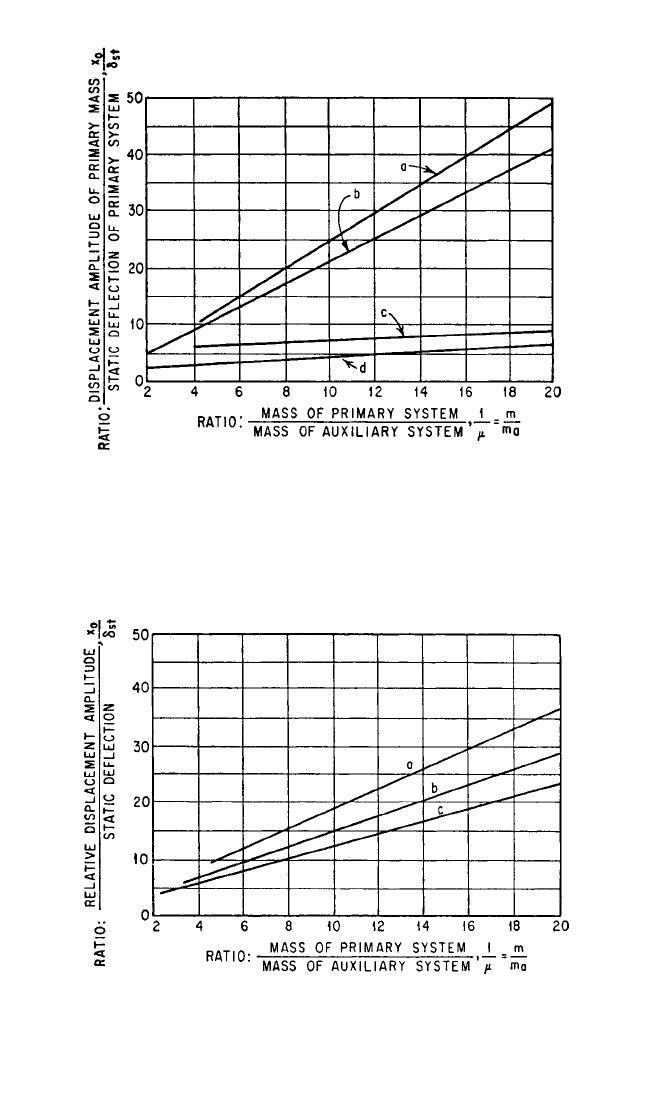
DYNAMIC VIBRATION ABSORBERS AND AUXILIARY MASS DAMPERS 6.15

FIGURE 6.15 Displacement amplitude of the primary mass as a function

of the size of the auxiliary mass: (a) auxiliary system coupled only by

Coulomb friction (α=0) with optimum damping; (b) auxiliary system cou-

pled only by viscous damping (α=0) of optimum value; (c) auxiliary system

coupled by spring and damper tuned to frequency of primary system (α=

1) with optimum damping; (d) auxiliary system coupled by spring and

damper with optimum tuning [α=1/(1 +µ)] and optimum damping.

FIGURE 6.16 Relative displacement amplitude between the primary

mass and the auxiliary mass as a function of the size of the auxiliary mass:

(a) auxiliary system coupled by spring and damper with optimum tuning

[α=1/(1 +µ)] and optimum damping; (b) auxiliary system coupled only by

viscous damping (α=0) of optimum value; (c) auxiliary system coupled by

spring and damper tuned to frequency of primary system (α=1) with opti-

mum damping.

8434_Harris_06_b.qxd 09/20/2001 11:26 AM Page 6.15

The Use of Auxiliary Mass Absorbers for Vibration Energy Dissipation.

When a complicated mass-spring system is analyzed for possible vibration troubles,

it is customary to compute the natural frequencies of the several modes of vibration

of the system. The vibration amplitudes and stresses are estimated by making an

energy balance between the energy input from the various exciting forces and the

energy dissipated in the system and external reactions. From this point of view, it is

desirable to know how much energy is dissipated in auxiliary mass systems and what

value the damping constant should have in an auxiliary mass system of limited size

to give maximum energy absorption. This is not the best criterion for determining

the optimum damping because it neglects the effects of damping upon the mode

shapes and the frequencies of the system, but it is generally adequate when com-

pared with the other uncertainties of the calculations. Methods of designing

dampers for torsional systems are given in Chap. 38.

Optimum Viscous Damping to Give Large Energy Absorption in an Auxiliary

Mass Absorber.

Suppose the amplitude of motion of the primary system is unaf-

fected by the auxiliary mass system which is attached to it. All energy absorption

occurs in the damping element of the auxiliary mass system and is obtained by inte-

grating the differential work done in the damper over a vibration cycle. The force

exerted by damping is c ˙x

(the subscripts a are dropped), where x

is the relative

motion and the increment of work is c ˙x

= c ˙x

dt. If x

= x

r 0

cos ωt, the work done

over a cycle is

V =



cω

r 0

sin

ωt dt =πcx

r 0

ω (6.29)

For a damper attached to a support moving in harmonic motion of amplitude x

the relative motion x

is given by Eq. (6.1). The amplitude of relative motion is

6.16 CHAPTER SIX

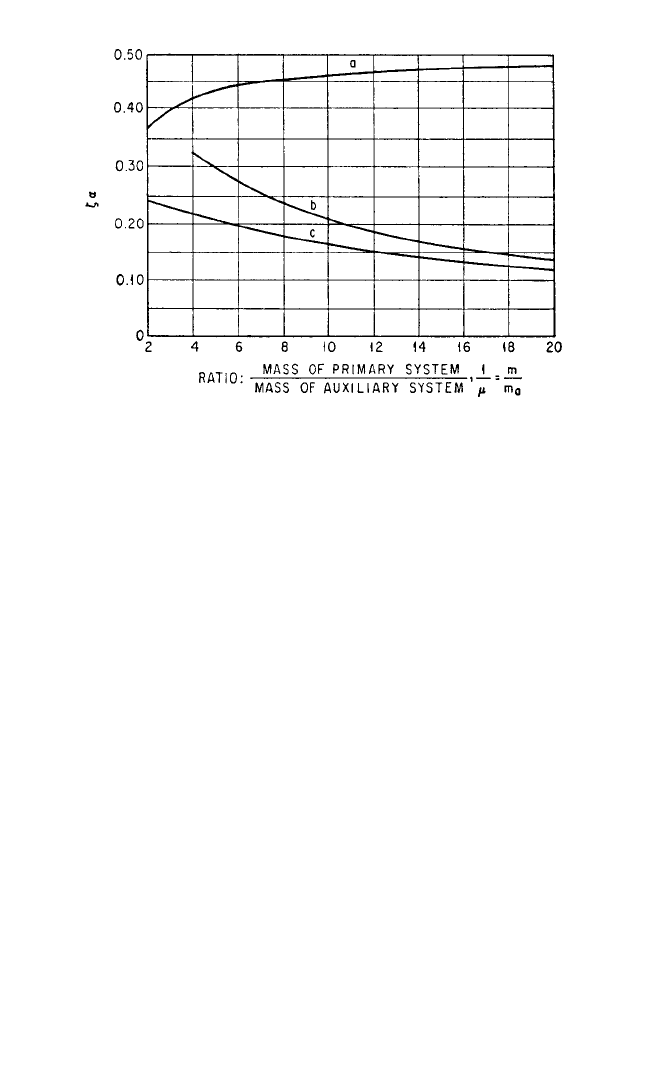
FIGURE 6.17 Curves showing damping required in auxiliary mass systems

to minimize vibration amplitude of primary system: (a) auxiliary mass cou-

pled by viscous damping only (α=0); (b) auxiliary system coupled by spring

and damper tuned to frequency of primary system (α=1); (c) auxiliary sys-

tem coupled by spring and damper with optimum tuning [α=1/(1 +µ)]. The

ordinate of the curves is ζα, where ζ is the fraction of critical damping in the

auxiliary system [Eq. (6.4)] and α is the tuning parameter [Eq. (6.15)].

8434_Harris_06_b.qxd 09/20/2001 11:26 AM Page 6.16

r 0

Substituting the above value of x

in Eq. (6.29) and integrating,

V == (6.30)

Equation (6.30) can be used to find the tuning and the damping that gives the max-

imum energy dissipation when the amplitude of the forcing motion remains con-

stant. Placing ∂V/∂β

= 0, the optimum value of β

for given values of ζ is found from

(β

)

opt

= (2ζ

− 1) ± 2 1



−



(6.31)

Placing ∂V/∂ζ = 0, the optimum value of ζ for a given value of β

opt

= (6.32)

Where k = 0, the optimum damping is determined most conveniently by setting

∂V/∂c = 0, using the dimensional form of Eq. (6.30), and determining c for maximum

energy absorption:

opt

= mω (6.33)

Auxiliary Mass Damper Using Coulomb Friction Damping.

Dampers relying

on Coulomb friction (i.e., friction whose force is constant) have been widely used. A

damper relying on dry friction and connected to its primary system with a spring is

too complicated to be analyzed or to be adjusted by experiment. For this reason, a

damper with Coulomb friction has been used with only friction damping connecting

the seismic mass (usually in a torsional application) to the primary system.

1,2,9

Because the motion is irregular, it is necessary to use energy methods of analysis.

The analysis given here applies to the case of linear vibration. By analogy, the appli-

cation to torsional or other vibration can be made easily (see Table 2.1 for analogous

parameters).

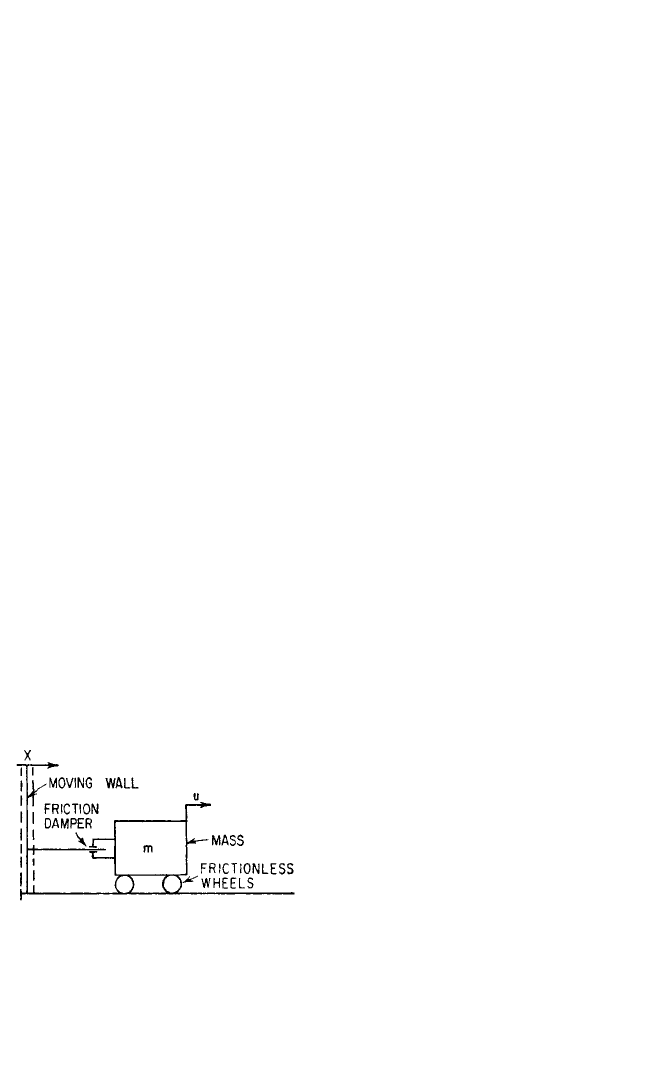
Consider the system shown in Fig.

6.18. It consists of a mass resting on

wheels that provide no resistance to

motion and are connected through a

friction damper to a wall that is moving

sinusoidally. The friction damper con-

sists of two friction facings that are held

on opposite sides of a plate by a spring

that can be adjusted to give a desired

clamping force. The maximum force that

can be transmitted through each inter-

face of the damper is the product of the

normal force and the coefficient of friction; the maximum total force for the damper

is the summation over the number of interfaces.

Consider the velocity diagrams shown in Fig. 6.19A, B, and C. In these diagrams

the velocity of the moving wall, ˙x = x

ω sin ωt, is shown by curve 1; the velocity ˙u of

the mass is shown by curve 2. The force exerted by the damper when slipping occurs

is F

. When F

≥ mü, the mass moves sinusoidally with the wall. When F

< mü, slip-

1 −β



2β

πx

mω

(2ζβ

)β



(1 −β

)

+ (2ζβ

)

πcωx



(k − mω

)

+ c



(1



−



)



(



ζβ



)



mω



(k



−



)



DYNAMIC VIBRATION ABSORBERS AND AUXILIARY MASS DAMPERS 6.17

FIGURE 6.18 Schematic diagram of auxiliary

mass absorber with Coulomb friction damping.

8434_Harris_06_b.qxd 09/20/2001 11:26 AM Page 6.17

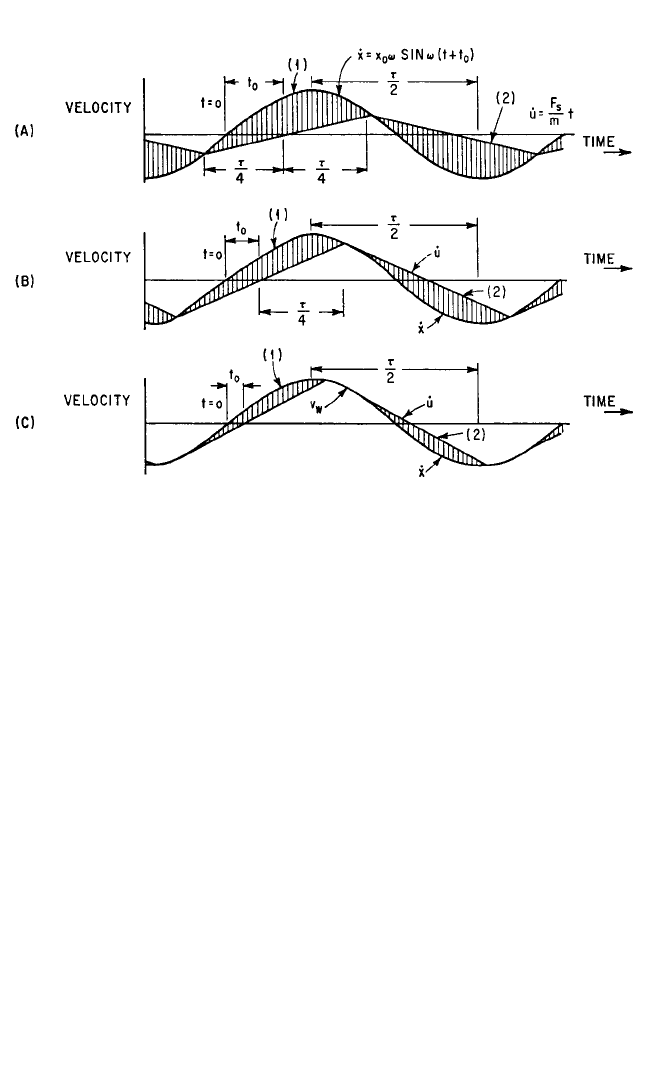
ping occurs in the damper and the mass is accelerated at a constant rate. Since a con-

stant acceleration produces a uniform change in velocity, the velocity of the mass

when the damper is slipping is shown by straight lines.The relative velocity between

the wall and the mass is shown by the vertical shading.

Figure 6.19A applies to a damper with a low friction force. The damper slips con-

tinuously. In Fig. 6.19B the velocities resulting from a larger friction force are shown.

Slipping disappears for certain portions of the cycle. Where the wall and the mass

have the same velocity, their accelerations also are equal. Slipping occurs when the

force transmitted by the damper is not large enough to keep the mass accelerating

with the wall. Since at the breakaway point the accelerations of the wall and mass

are equal, their velocity-time curves have the same slope; i.e., the curves are tangent

at this point. In Fig. 6.19C, the damping force is so large that the mass follows the

wall for a considerable portion of the cycle and slips only where its acceleration

becomes greater than the value of F

/m. A slight increase in the clamping force or in

the coefficient of friction locks the mass to the wall; then there is no relative motion

and no damping.

Because of the nature of the damping force, the damping provided by the friction

damper can be computed most practically in terms of energy. If the friction force

exerted through the damper is F

, the energy dissipated by the damper is the prod-

uct of the friction force and the total relative motion between the mass and the mov-

ing wall.The time reference is taken at the moment when the auxiliary mass m has a

zero velocity and is being accelerated to a positive velocity, Fig. 6.19A. Let the period

of the vibratory motion of the wall be τ=2π/ω, where ω is the angular frequency of

the wall motion. By symmetry, the points of no slippage in the damper occur at times

6.18 CHAPTER SIX

FIGURE 6.19 Velocity-time diagrams for motion of wall (curve 1) and mass (curve 2) of Fig.

6.18. The conditions for a small damping force are shown at (A), for an intermediate damping

force at (B), and for a large damping force at (C). The relative velocity between the wall and the

mass is indicated by vertical shading.

8434_Harris_06_b.qxd 09/20/2001 11:26 AM Page 6.18

−τ/4, τ/4, and 3τ/4. Let the time when the velocity of the wall is zero be −t

; then the

velocity of the wall ˙x is

˙x =+x

ω sin ω(t + t

)

The velocity ˙u of the mass for −τ/4 < t <τ/4 is

˙u = üt = t

The velocities of the wall and the mass are equal at time t =τ/4:

ω sin ω



+ t



Since ωτ/4 =π/2, sin ω(τ/4 + t

) = cos ωt

. Therefore

cos ωt

The relative velocity between the moving wall and the mass is ˙x − ˙u, and the total rel-

ative motion is the integral of the relative velocity over a cycle. Note that the area

between the two curves for the second half of the cycle is the same as for the first.

Hence, the work V per cycle is

V = 2 

τ/4

−τ/4

(˙x − ˙u) dt = 4F



1 −

 

(6.34)

Optimum damping occurs when the work per cycle is a maximum. It can be deter-

mined by setting the derivative of V with respect to F

in Eq. (6.34) equal to zero and

solving for F

)

opt

= mω

(6.35)

Energy absorption per cycle with optimum damping is, from Eq. (6.34),

opt

= mω

(6.36)

A comparison of the effectiveness of the Coulomb friction damper with other types

is given in Fig. 6.15.

EFFECT OF NONLINEARITY IN THE SPRING OF

AN AUXILIARY MASS DAMPER

It is possible to extend the range of frequency over which a dynamic absorber is effec-

tive by using a nonlinear spring.

10–12

When a nonlinear spring is used, the natural fre-

quency of the absorber is a function of the amplitude of vibration; it increases or

decreases, depending upon whether the spring stiffness increases or decreases with

deflection. Figure 6.20A shows a typical response curve for a system with increasing

spring stiffness; Fig. 6.20B illustrates types of systems having increasing spring stiff-

ness and shows typical force-deflection curves. Figure 6.21A shows a typical response



2





2mx



DYNAMIC VIBRATION ABSORBERS AND AUXILIARY MASS DAMPERS 6.19

8434_Harris_06_b.qxd 09/20/2001 11:26 AM Page 6.19

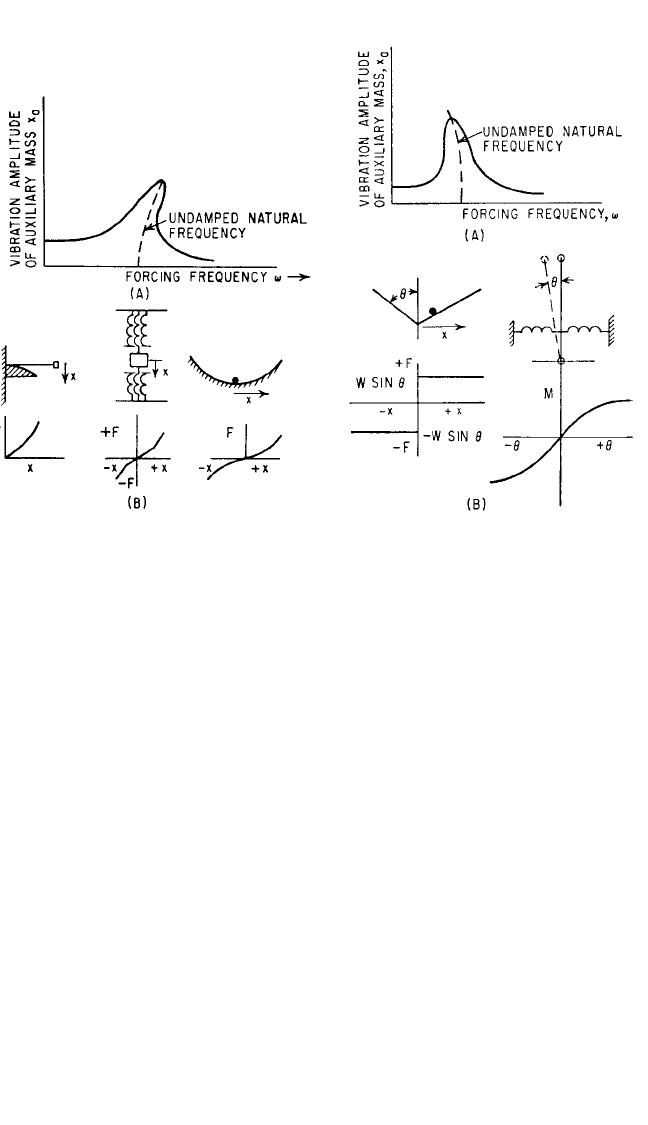
curve for a system of decreasing spring stiffness; Fig. 6.21B illustrates types of systems

having decreasing stiffnesses and shows typical force-deflection curves.

To compute the equivalent mass at a given frequency when a nonlinear spring is

used, it is necessary to use a trial-and-error procedure. By the methods given in

Chap. 4, compute the natural frequency of the auxiliary mass system, assuming the

point of attachment fixed, as a function of the amplitude of motion of the auxiliary

mass. This will result in a curve similar to the dotted curves in Figs. 6.20A and 6.21A.

At the given frequency, compute β

in Eq. (6.4) in terms of the tuned frequency of

the absorber at zero amplitude. (The tuned frequency will change with amplitude

because the spring constant changes.) With this value of β

compute the equivalent

mass from Eq. (6.6). With this mass in the system, compute the amplitude of motion

of the primary mass to which the auxiliary system is attached [Eq. (6.7)] and the

amplitude of the relative motion x

r 0

= v

(1 − v

. Using this value of x

r 0

, ascertain

the corresponding value of resonance frequency of the system from the computed

curve, and compute the new value of β

. Repeat the process until the value of β

remains unchanged upon repeated calculation.

A dynamic absorber having a nonlinear characteristic can be used to introduce

nonlinearity into a resonant system. This can be useful in the case where a machine

passes through a resonance rapidly as the speed is increased but slowly as the speed is

decreased. In bringing this machine up to speed, there is a natural frequency that

comes into strong resonance, giving a critical speed. A strongly nonlinear dynamic

absorber tuned at low amplitudes to the optimum frequency for the damped absorber

6.20 CHAPTER SIX

FIGURE 6.20 Auxiliary mass damper with

nonlinear spring having stiffness that increases

as deflection increases. The response to forced

vibration and the natural frequency are shown

at (A). Several arrangements of nonlinear sys-

tems with the corresponding force-deflection

curves are shown at (B).

FIGURE 6.21 Auxiliary mass damper with

nonlinear spring having stiffness that decreases

as deflection increases. The response to forced

vibration and the natural frequency are shown

at (A). Two arrangements of nonlinear systems

with the corresponding force-deflection curves

are shown at (B).

8434_Harris_06_b.qxd 09/20/2001 11:26 AM Page 6.20

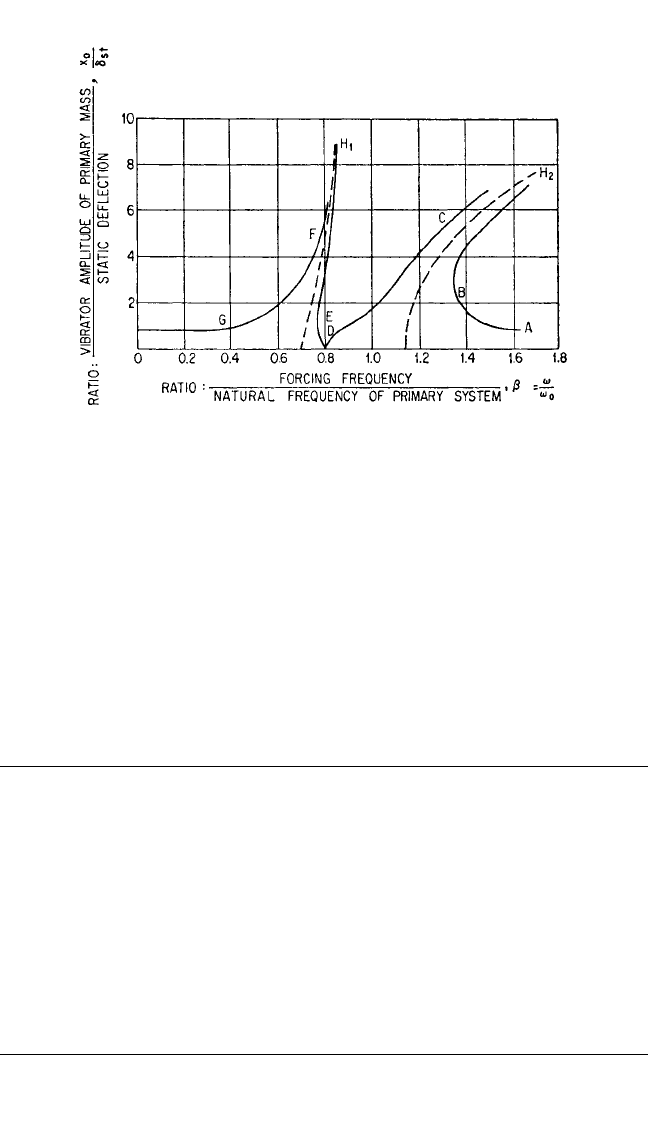
can be used to reduce the effects of the critical speed.Two resonant peaks will be intro-

duced, as shown on curve 1 of Fig. 6.13. By making the dynamic absorber nonlinear, so

that the stiffness becomes greater as the amplitude of vibration is increased, the peaks

are bent over to provide the response curve shown in Fig. 6.22. In starting, the machine

is accelerated through the two critical speeds so fast that a resonance is unable to build

up. In coasting to a stop, there would be ample time for significant amplitudes to build

up if the nonlinearity did not exist. Because of the nonlinearity, the amplitude of vibra-

tion as a function of speed (since β is proportional to speed) follows the path A, B, C,

D, E, F, G and never reaches the extreme amplitudes H

and H

MULTIMASS ABSORBERS

In general, only one mass is used in a dynamic absorber. However, it is possible to

provide a dynamic absorber that is effective for two or more frequencies by attach-

ing an auxiliary mass system that resonates at the frequencies that are objectionable.

The principle that would make such a dynamic absorber effective is utilized in the

design of the elastic system of a ship’s propulsion plant driven by independent high-

pressure and low-pressure turbines. By making the frequencies of the two branches

about the reduction gear identical, the gear becomes a node for one of the resonant

modes. Then it is impossible to excite the mode of vibration where one turbine

branch vibrates against the other as a result of excitation transmitted by the pro-

peller shaft to that node.

DISTRIBUTED MASS ABSORBERS

It is possible to use distributed masses as vibration dampers. Consider an undamped

rod of distributed mass and elasticity attached to a foundation that vibrates the rod

DYNAMIC VIBRATION ABSORBERS AND AUXILIARY MASS DAMPERS 6.21

FIGURE 6.22 Motion of the primary mass, as a function of forcing fre-

quency, in a system having a nonlinear dynamic absorber whose natural fre-

quency increases with amplitude. The mass of the absorber is 0.25 times the

mass of the primary system (µ=0.25).

8434_Harris_06_b.qxd 09/20/2001 11:26 AM Page 6.21

axially, as shown in Fig. 6.23. The differential equation for the motion of this rod is

derived in Chap. 7. The values of the constants are set by the boundary conditions:

Stress = E = 0 where x = l

(6.37)

u = u

cos ωt where x = 0

The solution of the equation of motion is

u = u

cos ωt



cos



x + tan



l sin





(6.38)

= u

cos ωt

where E is the modulus of elasticity and γ is the weight density of the material.When

x = 0, the force F on the foundation is

F = SE



= SEu





tan





(6.39)

where S is the cross-sectional area of the bar. It is apparent that as the argument of

the tangent has successive values of π/2, 3π/2, 5π/2,...,the force exerted on the

foundation becomes infinite. The distributed mass acts as a dynamic absorber

enforcing a node at its point of attachment. By tuning the mass so that



l = or l =



(6.40)

the distributed mass acts as a dynamic absorber for not only the fundamental fre-

quency ω/2π but also for the third, fifth, seventh,...harmonics of the fundamental.

The above solution neglects damping. It is possible to consider the effect of

damping by including a damping term in the differential equation. The stress in an

element is assumed to be the sum of a deformation stress and a stress related to the

velocity of strain:

σ=E +µ (6.41)

where ε=∂u/∂x is the strain. Then the

differential equation becomes

E +µ = (6.42)

Since the absorber is excited by a founda-

tion moving with a frequency f =ω/2π,

u may be expressed as Ru

jωt

and the par-

tial differential equation can be written as

the ordinary linear differential equation

E + jωµ + = 0

This equation may be written

γω



∂



∂t



∂



∂x

∂t

∂



∂x

d



nπ



2ω

nπ



γω



γω



γω



∂u



∂x

cos γ



(1 − x)



cos γ



γω



γω



γω



∂u



∂x

6.22 CHAPTER SIX

FIGURE 6.23 Elastic body with distributed

mass used as auxiliary mass damper.

8434_Harris_06_b.qxd 09/20/2001 11:26 AM Page 6.22



1 +



+ u

= 0 (6.43)

Since Eq. (6.43) is a second-order linear differential equation, the solution may be

written

u = A

+ A

(6.44)

where β

and β

are the two roots of the equation

= (6.45)

For small values of µ, by a binomial expansion of the denominator,

±β =



+ j



ω (6.46)

where µ is defined by Eq. (6.41).

The boundary conditions to be met by the damper are:

At x = 0: u = u

therefore, A

+ A

= u

(6.47)

At x = l: σ=(E + jωµ) = 0 therefore, A

βl

− A

−βl

= 0

Solving Eqs. (6.47) for A

and A

and substituting the result in Eq. (6.44),

u = u

(6.48)

The force exerted on the foundation by the damper is

(x = 0)

= Sσ

(x = 0)

=−Su

(E + jωµ) β tanh βl (6.49)

where S is the cross-section area of the bar. When the complex value of β as given in

Eq. (6.46) is substituted in Eq. (6.49), the following value for the dynamic force

exerted on the foundation is obtained:

(x = 0)



1 +



sin 2





ωl



+ sinh





ωl





ωu

cos 2





ωl



+ cosh





ωl



+ j

sin 2





ωl



−



1 +



sinh







(6.50)

cos 2





ωl



+ cosh





ωl



A plot of the real and imaginary values of F

(x = 0)

/SE



ωu

is given in Fig. 6.24 for

zero damping and for a damping coefficient µω/E = 0.1 as a function of a tuning



µω



µω



µω



µω



µω



µω



cosh β(l − x)



cosh βl

∂u



∂x



µω



−(γ/E

)ω



1 + (jµω/E)

γω



µωj



DYNAMIC VIBRATION ABSORBERS AND AUXILIARY MASS DAMPERS 6.23

8434_Harris_06_b.qxd 09/20/2001 11:26 AM Page 6.23

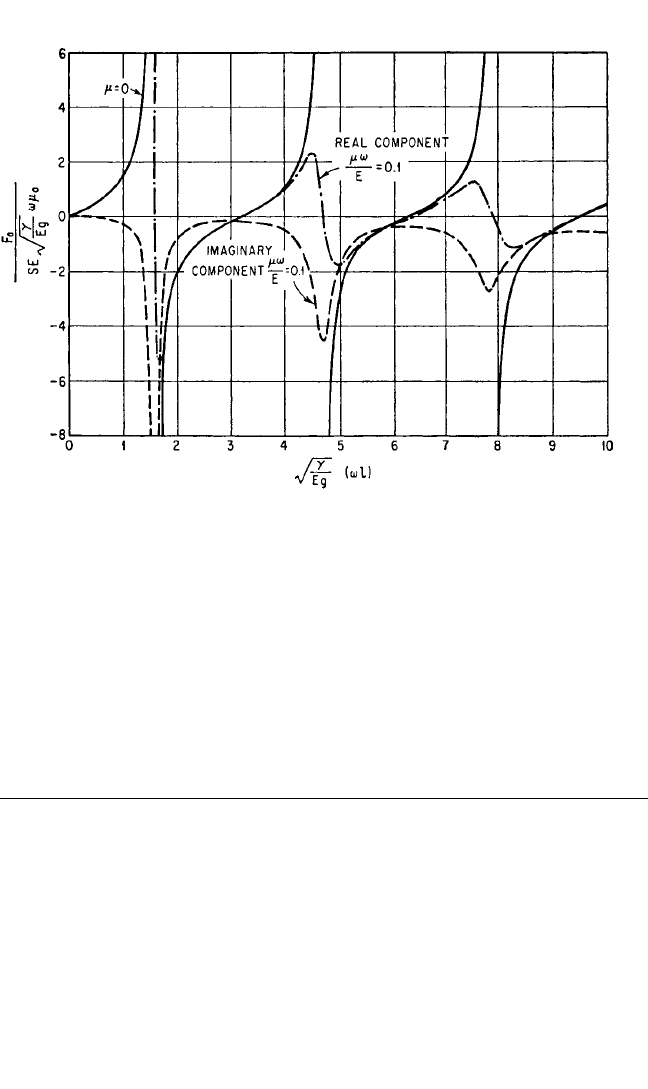
parameter γ/



(ω



. Damping decreases the effectiveness of the distributed mass

damper substantially, particularly for the higher modes.

Use of a distributed mass as a vibration absorber is practical only at very high fre-

quency; otherwise, too long a length is required.

PRACTICAL APPLICATIONS OF AUXILIARY MASS

DAMPERS AND ABSORBERS TO SINGLE

DEGREE-OF-FREEDOM SYSTEMS

THE DYNAMIC ABSORBER

The dynamic absorber, because of its tuning, can be used to eliminate vibration only

where the frequency of the vibration is constant. Many pieces of equipment to which

it is applied are operated by alternating current. So that it can be used for time keep-

ing, the frequency of this alternating current is held remarkably constant. For this

reason, most applications of dynamic absorbers are made to mechanisms that oper-

ate in synchronism from an ac power supply.

An application of a dynamic absorber to the pedestal of an ac generator having

considerable vibration is shown in Fig. 6.25, where the relative sizes of absorber and

pedestal are shown approximately to scale. In this case, the application is made to a

complicated structure and the mass of the absorber is much less than that of the pri-

mary system; however, since the frequency of the excitation is constant, the dynamic

6.24 CHAPTER SIX

FIGURE 6.24 Real and imaginary components of the force applied to a vibrating body by the dis-

tributed mass damper shown in Fig. 6.23. These relations are given mathematically by Eq. (6.50), and

the terms are defined in connection with Eq. (6.38). The curves are for a value of the damping coeffi-

cient µω/E = 0.1, where µ is defined by Eq. (6.41).

8434_Harris_06_b.qxd 09/20/2001 11:26 AM Page 6.24