Хамухин А.А. Введение в информатику для инженеров нефтегазового дела:
Подождите немного. Документ загружается.

Лагранжа. В этом фрагменте первый цикл (по переменной i) предназначен для
расчета суммы в формуле 4.8. Второй, вложенный цикл (по переменной j)
предназначен для расчета произведения в формуле 4.8.
Фрагмент такой же программы для локальной интерполяции:
S = 0
For i = Nz – Nleft To Nz + Nright
p = 1
For j = Nz – Nleft To Nz + Nright
If j <> i And j <> Nz Then p = p * ((X(Nz) – X(j)) / (X(i) – X(j)))
Next j
If i <> Nz Then S = S + Y(i) * p
Next i
Y(Nz) = S
Где Nleft, Nright – количество точек (узлов интерполяции) слева и справа от
расчетной (дефектной) точки, участвующих в ее восстановлении.
4.4.3. Экстраполяция
В отличие от интерполяции, предназначенной для расчета внутренних или
промежуточных значений, экстраполяция предназначена для расчета точек,
координаты которых выходят за пределы заданного ряда данных. Все расчетные
формулы (и, соответственно, программы) остаются почти такими же. Разница при
составлении программы заключается только в изменении заголовков циклов:
For i = N – Nprog To N,
где (Nprog+1) – количество последних точек в заданном ряде данных, которое
мы используем для расчета следующей точки за пределами ряда (N+1). Аналогично
необходимо заменить и заголовок цикла по переменной j.
4.5. Сглаживание экспериментальных данных
Функциональная задача сглаживания экспериментальных данных возникает не
только из-за необходимости снизить влияние случайных помех на исследуемую
величину, но и для того чтобы ограничить влияние множества прочих объективно
существующих факторов для уточнения влияния одного фактора.
Одно из самых распространенных – кусочно-линейное сглаживание, когда через
все экспериментальные точки проводятся отрезки прямых линий. Иногда
применяются логарифмические шкалы по осям координат. В некоторых случаях,
может использоваться и более сложная, чем линейная, например, – квадратичная
функция. Широко известен метод скользящего среднего, когда несколько идущих
подряд точек заменяется их средним значением.
В общем случае задача сглаживания экспериментальных данных решается с
помощью методов аппроксимации.
121
4.5.1. Аппроксимация
Наиболее распространенным методом аппроксимации экспериментальных
данных является метод наименьших квадратов. Метод позволяет использовать
аппроксимирующие функции произвольного вида и относится к группе глобальных
методов.
Простейшим вариантом метода наименьших квадратов является аппроксимация
прямой линией (полиномом первой степени). Этот вариант метода наименьших
квадратов носит также название линейной регрессии.
Критерием близости в методе наименьших квадратов является требование
минимальности функционала F, являющегося суммой квадратов отклонений
аппроксимирующей функции от экспериментальных точек:
∑
=
→−=
N
i
ii
xfyФ
1
2
min))((
. (4.10)
Таким образом, не требуется, чтобы аппроксимирующая функция проходила
через все заданные точки (как при интерполяции), что особенно важно при
аппроксимации данных, заведомо содержащих погрешности.
Важной особенностью метода является то, что аппроксимирующая функция
может быть произвольной. Ее вид определяется особенностями решаемой задачи,
например, физическими, если проводится аппроксимация результатов физического
эксперимента. Наиболее часто применяется аппроксимация полиномом некоторой
степени (полиномиальная регрессия) и аппроксимация комбинацией произвольных
функций.
Кроме того, часто возможно путем замены переменных свести задачу к
линейной (провести линеаризацию).
4.5.2. Аппроксимация линейной функцией
Задан ряд экспериментальных данных, состоящий из пар чисел (X
i
, Y
i
), i
=1,…,N. Где X
i
– независимая координата, заданная обычно с некоторым
(постоянным) шагом, Yi – результат измерения некоторой величины (высоты
рельефа местности, глубины верхней границы нефтяного пласта и т.п.).
Требуется по этим данным построить линейную аппроксимирующую функцию
вида
baXXf
+
=)(
, (4.11)
такую, чтобы сумма квадратов отклонений экспериментальных данных от
расчетных в заданных точках была минимальна.
Неизвестными параметрами в этой задаче являются коэффициенты a b
аппроксимирующей функции.
Решение
Запишем указанный в 4.10 функционал для заданной аппроксимирующей
функции:
122

min)())((
2
1
2
1
→−+=−=
∑∑
==
i
N
i
ii
N
i
i
YbaXYXfФ
. (4.12)
Из математического анализа известно, что минимум функционала достигается
при равенстве нулю всех его частных производных по независимым переменным.
Таким образом, запишем условия минимума нашего функционала:
.0
;0
=
∂
∂
=
∂
∂
b
Ф
a
Ф
(4.13)
Или, после подстановки и взятия частной производной, получим систему из
двух уравнений:
(4.14)
Решая эту систему, с помощью преобразований получаем:
(4.15)
(4.16)
Далее, задавая значения X
i
с некоторым шагом, вычисляем по найденным
коэффициентам f(X
i
) и строим график (рис. 4.4). Как видно из графика, точность
прогноза с помощью линейной аппроксимации относительно невысока, поэтому ее
используют хотя и часто, но только для предварительных оценок и выявления
тенденций изменения экспериментальных данных.
).*(
1
;
)()(*
***
1
11
22
11
i
N
i
i
N
i
N
i
ii
N
i
N
i
N
i
iiii
XaY
N
b
XXN
YXYXN
a
−=
−
−
=
∑
∑∑
∑∑∑
=
−=
==
1=
(
1
1
∑
∑
=
=
=−+
N
ii
N
i
i
YbaX
aX
.01)(2
;
0)2 =−+
ii
XYb
i
123
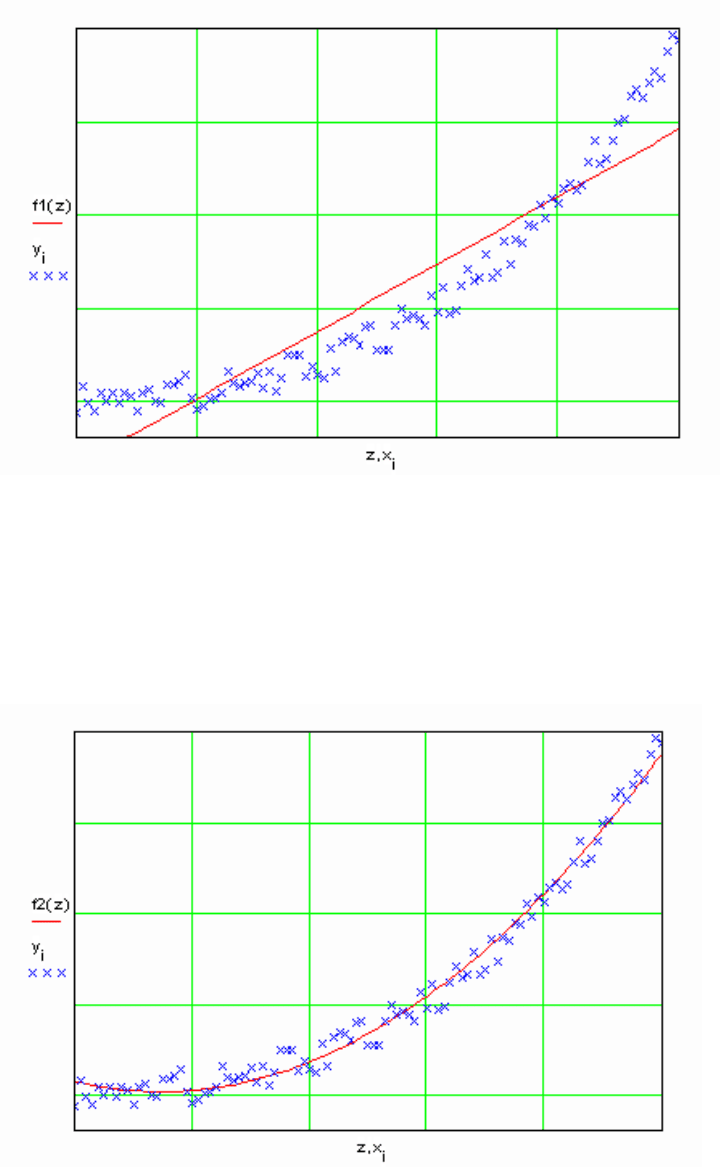
Рис. 4.4. Пример линейной аппроксимации (сплошная линия) экспериментальных данных
4.5.3. Аппроксимация квадратичной функцией и другими
функциями
Для повышения точности математической модели используют более сложные
аппроксимирующие функции, например, полиномы второго порядка (рис. 4.5).
Рис. 4.5. Пример квадратичной аппроксимации (сплошная линия) экспериментальных данных
При аппроксимации квадратичной функцией задача формулируется следующим
образом.
Задан ряд экспериментальных данных, состоящий из пар чисел (Xi, Yi), i=1,…,N.
124
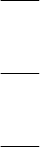
Требуется по этим данным построить квадратичную аппроксимирующую
функцию вида:
cbXaXXf ++=
2
)(
. (4.17)
Неизвестными параметрами в этой задаче являются коэффициенты a, b, с
аппроксимирующей функции. Порядок решения таких задач полностью аналогичен
порядку, рассмотренному выше, только меняется вид выражений.
4.5.4. Решение методом наименьших квадратов (МНК)
Запишем указанный выше функционал (4.12) для заданной аппроксимирующей
функции (4.17):
.min)())((
2
1
22
1
→−++=−=
∑∑
==
ii
N
i
ii
N
i
i
YcbXaXYXfФ
(4.18)
Из математического анализа известно, что минимум функционала достигается
при равенстве нулю всех его частных производных по независимым переменным.
Таким образом, в соответствии с (4.12) запишем условие минимума нашего
функционала:
.0
;0
;0
=
∂
∂
=
∂
∂
=
∂
∂
с
Ф
b
Ф
a
Ф
(4.19)
Подставляем выражение функционала Ф и вычисляя производные, получим
систему из трех уравнений для трех неизвестных:
.01)(2
;0)(2
;0)(2
1
2
1
2
1
22
=−++
=−++
=−++
∑
∑
∑
=
=
=
ii
N
i
i
N
i
iiii
N
i
iiii
YcbXaX
XYcbXaX
XYcbXaX
(4.20)
125
Эта система легко решается относительно трех неизвестных, из которой можно
записать выражения для искомых коэффициентов (a, b, c).
Аналогично строятся аппроксимирующие функции и более сложного вида.
Подробнее с методами интерполяции и аппроксимации можно ознакомиться в
специальной литературе [13].
4.6. Расчет площадей и объемов, заданных координатами
контуров объектов
Одной из главных задач нефтегазогеологии является оценка запасов
разведанных месторождений. Для этого они экспериментально «оконтуриваются»,
то есть определяются координаты (на плоскости и в пространстве) границ залежей.
Затем по найденным координатам вычисляются их площади и объемы.
Математически эта задача известна как вычисление интеграла по контуру.
Аналитическое решение часто получить очень сложно, так как неизвестен вид
подынтегральной функции. Поэтому для решения подобных задач применят методы
численного интегрирования.
4.6.1. Численное интегрирование, общая постановка задачи
Пусть требуется вычислить определенный интеграл на интервале [a,b].
∫
b
a
dxxf )(
(4.21)
Далеко не всегда задача может быть решена аналитически. В частности,
численное решение требуется в том случае, когда подынтегральная функция задана
таблично.
Для численного интегрирования подынтегральную функцию аппроксимируют
какой-либо более простой функцией, интеграл от которой может быть вычислен.
Обычно в качестве аппроксимирующей функции используют полином. В случае
полинома нулевой степени мы получим формулу прямоугольников, в случае
полинома первой степени – формулу трапеций, в случае полинома второй
степени – формулу Симпсона. Все эти методы являются частными случаями
квадратурных формул Ньютона-Котеса. Примеры на графиках представлены
ниже на рис. 4.6. Очевидно, что чем меньше будет шаг дискретизации, тем выше
будет точность вычисления по любой из упомянутых выше формул. Зачастую на
практике увеличение количества точек, с помощью которых задается контур,
связано или с большими материальными затратами или просто невозможно из-за
тех или иных условий. Поэтому в инженерных расчетах важно уметь применять
такие формулы для вычисления интегралов, которые при одинаковом количестве
точек дают более высокую точность. Например, можно считать по формуле
прямоугольников и посылать бригаду геологов для топографической съёмки
местности, чтобы повысить точность путем увеличения точек оконтуривания в два
раза. А можно при том же количестве точек применить формулу Симпсона и
повысить точность расчета, не посылая в болота людей.
126
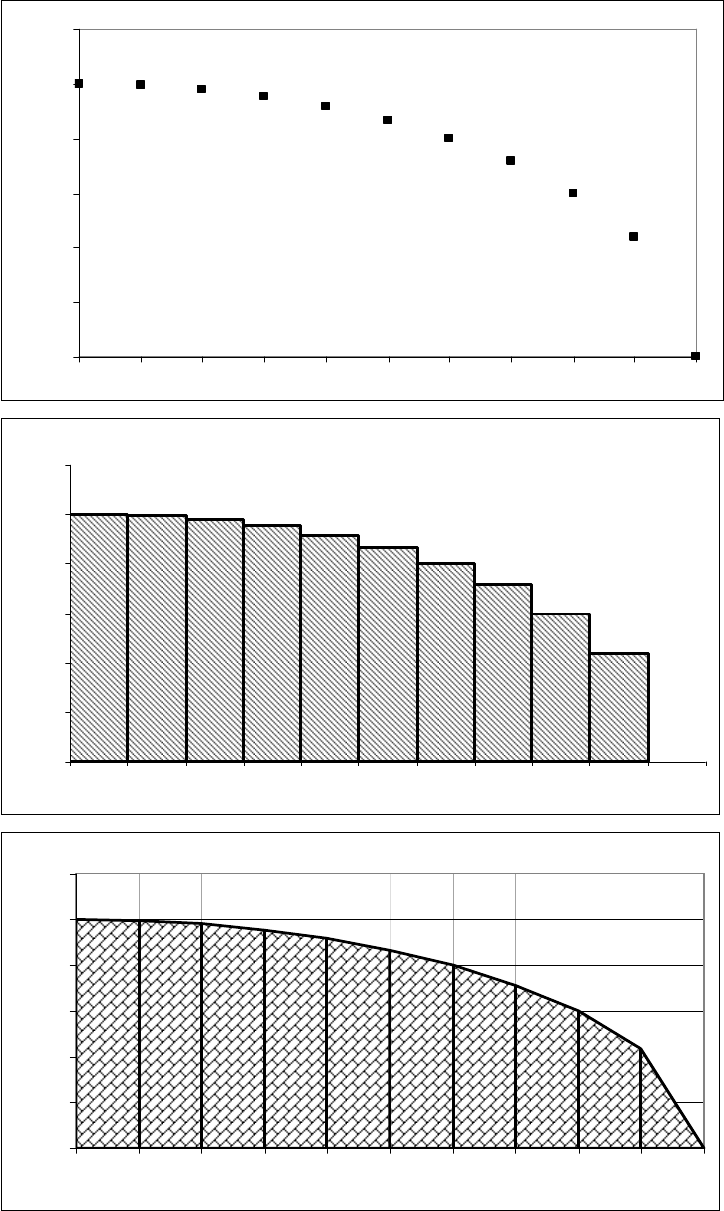
Исходный контур, заданный координатами
0,00
2,00
4,00
6,00
8,00
10,00
12,00
1234567891011
а
Формула прямоугольников
0,00
2,00
4,00
6,00
8,00
10,00
12,00
1234567891011
б
Формула трапеций , формула Симпсона
0,00
2,00
4,00
6,00
8,00
10,00
12,00
123456789101
1
в
Рис. 4.6. Пример вычисления площади контура, заданного координатами (а): б – по формулам
численного интегрирования с помощью прямоугольников, в – по формулам численного
интегрирования с помощью трапеций
127

4.6.2. Примеры решение задачи численного интегрирования
Метод прямоугольников, как наиболее простой здесь не рассматривается, и в
лабораторной работе его будем применять только для демонстрации снижения
погрешности расчета с помощью более точных методов на одном и том же наборе
экспериментальных данных
В методе трапеций подынтегральную функцию аппроксимируют полиномом
первой степени, то есть прямой линией. Это значит, что вместо площади
криволинейной трапеции мы будем искать площадь прямоугольной трапеции.
Приближенное значение интеграла равно:
)(
2
)()(
)( ab
afbf
dxxf
b
a
−
−
≈
∫
. (4.22)
Погрешность этой формулы пропорциональна остаточному члену O(h
3
f
””
), где h
− интервал интегрирования. Оценку значения интеграла можно сделать более
точной, если разбить интервал интегрирования (b-a) на n частей и применить
формулу трапеций для каждого такого интервала:
))19(...)2()()()((
2
1
)( hnafhafhafbfafhdxxf
b
a
−++++++++
⎟
⎠
⎞
⎜
⎝
⎛
≈
∫
. (4.23)
Формула трапеций дает результат, сильно зависящий от величины шага h, что
сказывается на точности вычисления определенного интеграла особенно в тех
случаях, когда функция имеет немонотонный характер. Можно предположить
повышение точности вычислений, если вместо отрезков прямых, заменяющих
криволинейные фрагменты графика функции f(x), использовать, например,
фрагменты парабол, проводимых через три соседних точки графика. Подобная
геометрическая интерпретация лежит в основе метода Симпсона для вычисления
определенного интеграла. Весь интервал интегрирования [a,b] разбивается на
четное число одинаковых отрезков n, длина отрезка также будет равна h=(b–a)/n.
Формула Симпсона имеет вид:
[]
)...(2)...(4)(
3
)(
2421531 −−
+++++++++≈
∫
nnba
b
a
fffffffff
h
dxxf
. (4.24)
В формуле выражения в скобках представляют собой суммы значений
подынтегральной функции соответственно на концах нечетных и четных
внутренних отрезков. Остаточный член формулы Симпсона пропорционален уже
четвертой степени шага:
128
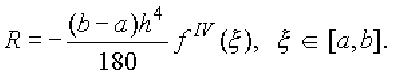
(4.25)
Существует множество других методов решения задачи численного
интегрирования, дающих более высокую точность расчета, например с помощью
формул Ньютона–Котеса. Более подробно с ними можно ознакомиться в
специальной литературе [13].
4.7. Поиск особых точек
Одной из самых важных функциональных задач в нефтегазогеологии является
поиск так называемых «особых точек» в экспериментальных данных. Это могут
быть минимумы или максимумы в профилях контуров нефтяных залежей, точки
пересечения различных линий уровня и т. п.
Визуализация этих данных в графическом виде до некоторых пор была едва ли
не единственным способом поиска таких точек Но в связи со значительным ростом
количества экспериментальных данных и применением компьютерных методов
обработки поиск особых точек также стали выполнять с помощью вычислительных
методов.
Для некоторых функциональных задач достаточного простого численного
дифференцирования, но чаще всего необходимо применение методов
последовательных приближений (итераций). Существует множество методов
последовательных приближений, из которых рассмотрим три, наиболее ярко
демонстрирующие те или иные подходы к решению подобных задач.
Это метод дихотомии (деления пополам) и метод хорд-касательных
(Ньютона). Для сравнения рассмотрим также метод Монте-Карло (случайного
поиска). В качестве «особых точек» будем рассматривать только точки
пересечения некоторой функцией (заданной таблично или аналитически) оси ОХ
(нули функции). К такой постановке могут быть сведены задачи поиска и других
видов особых точек, например, экстремумы можно находить, если заменить
целевую функцию ее первой производной, а точки перегиба можно находить, – если
заменить целевую функцию ее второй производной. Напомним, что точки
пересечения графика функции f(x) = 0 оси ОХ называются корнями этого
уравнения.
4.7.1. Численное дифференцирование
Численное дифференцирование применяется, когда аналитическое выполнить
невозможно из-за отсутствия точного математического описания функциональной
зависимости или его сложности.
На практике функциональная зависимость часто имеется только в виде
числовых рядов экспериментальных данных, представляющих собой изменение
некоторой наблюдаемой величины во времени и/или пространстве. Например, это
динамограмма станка-качалки нефти, которая строится с помощью показаний
электронных датчиков в определенные моменты времени, требует вычисления
производных по времени от изменения нагрузки на насос. С помощью вычисленных
129
значений производных можно определить эффективность работы насоса и выявить
причины ее снижения.
Численное дифференцирование очень чувствительно к погрешностям в
исходных данных, поэтому отбрасывание членов ряда должно применяться
осторожно и, по-возможности, с проверкой в реперных (заранее известных) точках.
Формулы численного дифференцирования основаны на конечных разностях.
Определение. Пусть задана функциональная зависимость Y в виде ряда данных
для равноотстоящих значений аргумента X.
XkXX
k
Δ+=
0
0,...)2,1,0( =k
1
>
=
−
=
Δ
+
hXXX
ii
. (4.26)
Первая конечная разность (нисходящая, вперед)
iii
YYY −=Δ
+1
(4.27)
и (восходящая, назад)
1−
−=Δ
iii
YYY . (4.28)
Вторая конечная разность (нисходящая)
iii
YYY Δ−Δ=Δ
+1
2
(4.29)
и (восходящая)
1
2
−
Δ−Δ=Δ
iii
YYY . (4.30)
Или, если подставить первую конечную разность нисходящую (4.27):
iiii
YYYY +−=Δ
++ 12
2
2
. (4.31)
Восходящая вторая конечная разность
21
2
2
−−
+−=Δ
iiii
YYYY . (4.32)
Центральная вторая конечная разность
11
2
2
−+
+−=Δ
iiii
YYYY . (4.33)
Третья конечная разность
iii
YYY
2
1
23
Δ−Δ=Δ
+
iiii
YYYY
−
+
−=
+++ 123
33 . (4.34)
Четвертая конечная разность
130
