Хамухин А.А. Введение в информатику для инженеров нефтегазового дела:

Подождите немного. Документ загружается.

Цикл Do-Loop позволяет внести в эту процедуру еще несколько изменений.

Например, в следующей программе Рro34 ключевое слово Do оставлено в начале

цикла, а условие завершения и ключевое слово Until переместились в его конец, за

ключевое слово Loop. В таком варианте цикл обязательно выполняется хотя бы

один раз, поскольку условие завершения не проверяется, пока не будут выполнены

все инструкции из тела цикла. Поэтому мы можем удалить инструкцию для

инициализации переменной L.

Sub Pro34()

Dim L As Integer

L = Int(100 * Rnd())

Beep

Loop Until L =7

MsgBox "Выпало число = " & L & ". Вы выиграли! (шутка)"

End Sub

А теперь заменим ключевое слово Until в конце цикла словом While. Тогда мы

сможем вернуть в условие знак неравенства вместо знака равенства:

Sub Pro35()

Dim L As Integer

L = Int(100 * Rnd())

Beep

Loop While L <> 7

MsgBox "Выпало число = " & L & ". Вы выиграли! (шутка)"

End Sub

Теперь приведем один из возможных вариантов реализации примера 30, только

вычислять будем не произведение, а сумму элементов массива.

Sub Pro36()

Dim Base(10) As Double

Dim Power As Integer

Dim Result As Double

Dim Count1 As Integer

Power = 5

Result = 0

Count1 = 1

Do Until Count1 > Power

Result = Result + Base(Count1)

Count1 = Count1 +1

Loop

MsgBox "Произведение первых 5 элементов массива = " & Result

End Sub

101

Обратите внимание, счетчик цикла (переменную Count1) здесь необходимо

увеличивать самим в теле цикла, в отличие от примера 30, где он увеличивался

автоматически. И начальное значение счетчика цикла необходимо задать самим до

начала цикла (инструкции Do Until). Изменилось по сравнению с примером 30 и

начальное значение результата (поскольку здесь мы вычисляем сумму, а не

произведение, его необходимо задать 0).

3.10.6. Управляющая инструкция For-Each-Next

Инструкция For-Each-Next предназначена для выполнения одной и той же

группы действий над каждым объектом семейства или элементом массива. Ниже

приведен простой пример этой инструкции:

Sub Pro37()

Dim CountryArray(5) As String

Dim Country As Variant

CountryArray(1) = " Finland"

CountryArray(2) = " Iceland"

CountryArray(3) = " New Zealand"

CountryArray(4) = " Denmark"

CountryArray(5) = " Singapore"

For Each Country In CountryArray

MsgBox Country

End Sub

В Рro37 элементы массива CountryArray заполняются названиями стран, с

наименьшим уровнем коррумпированности по возрастанию (по данным

Transparency International за 2006 г.), которые затем по очереди выводятся на экран

в структуре For-Each-Next.

Обратите внимание, что, как и в случае For-Next, инструкции цикла

выполняются определенное число раз, но здесь Вам не придется заботиться об

указании этого числа. Оно точно совпадает с количеством элементов массива (или

объектов семейства). Например, если увеличить размер массива до 127 (чтобы

увидеть в списке Россию), то код с циклом For-Each переделывать не надо.

Рассмотрим структуру цикла For-Each-Next подробнее.

For Each − ключевые слова, отмечающие начало инструкции For-Each-Next

Country − переменная, которой присваиваются значения элементов группы −

массива или семейства объекта. В первом случае переменная должна относиться к

типу Variant. Во втором случае Вы можете определить ее как Variant, Object или

приписать ей конкретный объектный тип, соответствующий объектам семейства.

In − ключевое слово, отделяющее переменную от группы

CountryArray − группа, то есть массив или семейство объектов. Количество

повторений цикла совпадает с числом элементов в группе. Переменной цикла при

первом выполнении присваивается значение первого элемента группы, затем – всех

последующих элементов.

MsgBox Country − действие, которое выполняется над элементом группы

102

Next − ключевое слово, отмечающее конец инструкции. Достигнув его,

программа возвращается к началу цикла — инструкции For-Each. Если значение

переменной цикла совпадет с последним элементом группы, выполнится

инструкция, написанная сразу после Next.

В инструкции For-Each-Next значения элементов массива можно использовать,

но нельзя изменять. На объекты семейств это ограничение не распространяется −

изменение их свойств в инструкции For-Each допустимо.

3.10.7. Инструкция For-Each-Next с семействами (объектами)

Преимущества For-Each-Next при работе с массивами бесспорны, но они

меркнут рядом с достоинствами этой структуры в обращении с объектами семейств.

Рассмотрим простой пример.

Sub Pro38()

Dim SheetVar As Worksheet

For Each SheetVar In ActiveWorkbook.Worksheets

MsgBox SheetVar.Name

End Sub

В Рrо38 происходит обращение к каждому рабочему листу из семейства

Worksheets активной рабочей книги, в результате которого имена листов

последовательно выводятся на экран, хотя их количество заранее программисту

неизвестно. Например, изменим значения свойств Name всех рабочих листов книги:

Sub Pro39()

Dim SheetVar As Worksheet

For Each SheetVar In ActiveWorkbook.Worksheets

SheetVar.Name = "Work" & SheetVar.Name

MsgBox SheetVar.Name

End Sub

Здесь изменяются имена листов: перед каждым из них добавляется слово Work.

Для восстановления прежних имен введите следующий фрагмент кода.

Sub Pro40 ()

Dim SheetVar As Worksheet

Dim x As Integer

x = 1

For Each SheetVar In ActiveWorkbook.Worksheets

SheetVar.Name = "Sheet" & x

x = x + 1

MsgBox SheetVar.Name

End Sub

103

Инструкцию For-Each-Next можно применять и для вызова методов объектов

семейства. Процедура Рro41 создает 10 новых рабочих книг, располагает их окна

мозаикой, а затем снова удаляет, оставляя лишь книгу, в которой размещена сама

процедура.

Sub Pro41()

Dim x As Integer

Dim Book As Workbook

For x = 1 To 10

Workbooks.Add

Next x

Windows.Arrange

MsgBox "Workbooks have been arranged"

For Each Book In Application Workbooks

If Book Name <> ThisWorkbook.Name Then

Book.Close

End If

ActiveWindow.WindowState = xlMaximized

End Sub

Десять новых рабочих книг создаются в цикле For-Next посредством обращения

к методу Add семейства Workbooks. Затем вызывается метод Arrange семейства

Windows, который упорядочивает расположение окон на экране. Далее выполнение

программы приостанавливается, чтобы Вы могли увидеть результаты и прочитать

сообщение в информационном окне.

3.11. Введение в проектирование интерфейса и

документирование

Если инженерные расчеты выполняются «для себя», то есть Вы не планируете,

что с Вашей программой будет работать кто-то другой, то этот раздел можно

пропустить. Хотя культура программирования требует, чтобы все функциональные

возможности программы, ее исходные данные и результаты расчета были

документированы, то есть имели «инструкцию для пользователя» даже если

программа пишется для себя (по истечению некоторого времени и сам автор может

забыть назначение данных). Если же Вы планируете свои расчеты оформить как

«программный продукт» или опубликовать, то этот этап будет одним из самых

важных. Поскольку именно от удобства «пользовательского интерфейса» и

понятности документации в большой степени зависит, будет ли спрос на Ваш

программный продукт.

В понятие «пользовательский интерфейс» включают обычно: 1) отображение на

экране рассчитываемых данных и форм для ввода исходных данных, 2) данные во

вводимых или выводимых файлах (базах данных), если таковые есть в программе, 3)

протоколы взаимодействия с различными внешними устройствами, если таковое

есть в программе. Документирование предполагает подробное описание всего

пользовательского интерфейса (обязательная часть), описание используемых в

104

программе принципов, методов, алгоритмов и т.п., помогающих пользователю

правильно использовать программу (необязательная, но желательная часть).

Для проектирования удобного и интуитивно понятного пользовательского

интерфейса операционные системы обычно предоставляют набор готовых

инструментов, который в ОС Windows называют элементами управления и

формами.

3.11.1. Основные элементы управления и формы Windows

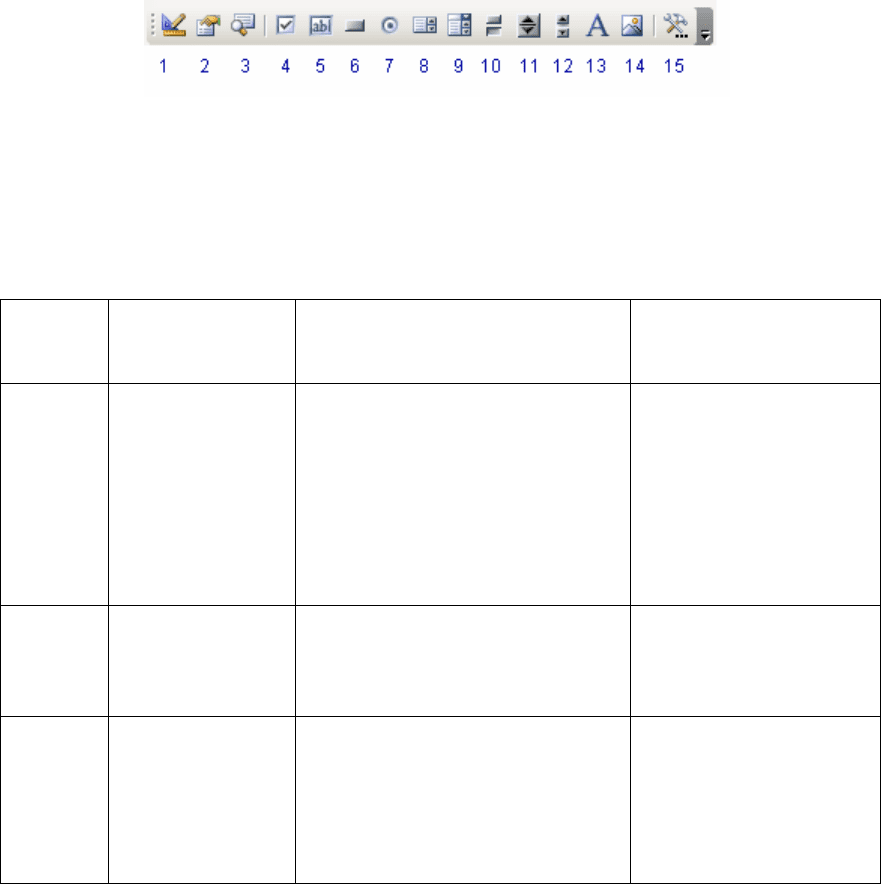
Элементы управления и формы Windows, если их нет на панели инструментов,

вызываются через меню Сервис–Настройка–Панели инструментов–Элементы

управления (рис. 3.1). Назначение элементов управления и примеры их

использования приведены в табл. 3.12.

Рис. 3.1. Вид панели пиктограмм элементов управления Windows

Таблица 3.12

Назначения элементов управления (ЭУ) Windows

(на месте многоточия в последнем столбце можно писать любой код, который будет

выполняться при щелчке на данном ЭУ)

Номер

пикто-

граммы

Наименование Назначение Фрагмент

вызываемой

программы

1 Режим

конструктора

При нажатой кнопке –

конструируем

пользовательский интерфейс

(размещаем ЭУ и набираем

под них программный код),

при отпущенной кнопке –

выполняем программы с

помощью размещенных ЭУ

–

2 Свойства Вызывается окно свойств

(Properties) активного

(выделенного) ЭУ, которые

можно задавать и изменять

–

3 Исходный

текст

Вызывается окно программ

VBA для всех размещенных

ЭУ, курсор появляется в окне

программы для активного

(выделенного) ЭУ, которую

можно набирать и изменять

–

105

Продолжение табл. 3.12

Номер

пикто-

граммы

Наименование Назначение Фрагмент

вызываемой

программы

Флажок

CheckBox

На экране размещается окно,

в котором щелчком мыши

можно поставить/убрать

флажок (галочку) при этом

переменная CheckBox1 будет

принимать значения

True/False соответственно.

Надпись возле флажка

изменяется с помощью

свойства Caption

Private Sub

CheckBox1_Click()

…

End Sub

Поле

TextBox

На экране размещается окно,

в котором можно набирать

любой текст (при отжатой

кнопке режим конструктора),

при этом он будет заноситься

в переменную TextBox1

Private Sub

TextBox1_Change()

…

End Sub

Кнопка

CommandButton

На экране размещается

кнопка для однократного

нажатия и выполнения

некоторой программы,

надпись на кнопке (в

соответствии с ее функцией)

изменяется с помощью

свойства Caption

Private Sub

CommandButton1_Clic

k()

…

End Sub

Переключатель

OptionButton

На экране размещается

кружок, в котором можно

ставить метку (переменная

OptionButton1 примет

значение True), причем если

на экране размещено

несколько переключателей, то

метка будет только в одном

после щелчка, с остальных

она снимется, а их

переменные примут значение

False

Private Sub

OptionButton1_Click()

…

End Sub

Private Sub

OptionButton2_Click()

…

End Sub

Список

ListBox

На экране размещается окно с

полосами прокрутки, в

котором можно выводить

значения любых переменных

(массивов) из программы

Private Sub

ListBox1_Click()

…

End Sub

106

Продолжение табл. 3.12

Номер

пикто-

граммы

Наименование Назначение Фрагмент

вызываемой

программы

9 Поле со

списком

ComboBox

Предназначено для ввода

данных из поля списка

возможных значений.

Сочетает в себе свойства

элементов управления

TextBox (текстовое поле) и

ListBox (список)

Private Sub

ComboBox1_Change()

…

End Sub

Выключатель

ToggleButton

На экране размещается

кнопка, сохраняющая нажатое

или отжатое положение. В

зависимости от этого

значение переменной

ToggleButton будет True или

False

Private Sub

ToggleButton1_Click()

…

End Sub

Счетчик

SpinButton

На экране размещается

кнопка-счетчик в виде двух

стрелок (горизонтальных или

вертикальных), нажимая на

которые можно увеличивать

или уменьшать значения

переменных

Private Sub

SpinButton1_Change()

…

End Sub

12 Полоса

прокрутки

ScrollBar

На экране размещается

вертикальная или

горизонтальная полоса, на

краях которой расположены

кнопки прокрутки, а внутри

перемещается бегунок.

Обычно полоса прокрутки

используется в паре с другим

элементом управления, в

котором может отображать

или с которого может

получать свое значение

Private Sub

ScrollBar1_Change()

…

End Sub

13 Надпись На экране размещается

прямоугольная область, в

которой можно набирать

любой текст, при щелчке по

этой области выполнится

программа, набранная в

заготовке (может

отсутствовать)

Private Sub

Label1_Click()

…

End Sub

107

Окончание табл. 3.12

Номер

пикто-

граммы

Наименование Назначение Фрагмент

вызываемой

программы

14 Рисунок На экране размещается

прямоугольная область, в

которой можно поместить

графический рисунок из

файла, при щелчке по этой

области выполнится

программа, набранная в

заготовке (может

отсутствовать)

Private Sub

Image1_Click()

…

End Sub

15 Другие

элементы

При щелчке по этой

пиктограмме появится список

с другими ЭУ, которые

можно использовать

ЭУ можно размещать как непосредственно в документе, так и на специальных

прямоугольных областях, называемых формами (UserForm). Для реализации

последнего варианта необходимо в редакторе VBA выполнить пункты меню Insert-

UserForm. Все загруженные диалоговые окна представляют коллекцию UserForms..

Элемент коллекции – объект класса UserForm задает отдельное окно, примеры

которого представлены на рис. 3.2 (конструирование формы) и 3.3 (вид формы во

время выполнения программы.

Рис. 3.2. Пример элементов управления в диалоговом окне (форме) при конструировании программы

108

Рис. 3.3. Пример элементов управления в диалоговом окне (форме) во время выполнения программы

UserForms это нормальная коллекция со стандартными методами и свойствами,

например, метод Item позволяет по имени или номеру добраться до любого ее

элемента, а метод Add добавляет новое диалоговое окно (форму) в коллекцию.

3.11.2. Интерфейс прикладных программ WinAPI

WinAPI (Application Programming Interface – интерфейс прикладных программ в

среде Windows) – это множество функций, организованных обычно в виде

библиотек с расширением DLL. Функции API позволяют организовать интерфейс

между прикладной программой и средой, в которой работает эта программа. Вызов

функций API позволяет программе получать доступ к ресурсам среды и управлять

ее работой.

Win32 – это название интерфейса, ориентированного на 32-х разрядные

приложения и реализованного на таких известных платформах как Windows 95,

Windows 98, Windows NT, Windows CE. Функции, составляющие этот интерфейс,

позволяют прикладной программе получать доступ к ресурсам операционной

системы и управлять ее работой. Функции, составляющие Win32 интерфейс,

организованы в виде нескольких динамически подключаемых библиотек DLL и

исполняемых файлов, например, Kernel32.dll, User32.dll, GDI32.dll и др. Любое из

приложений, работающее в среде Windows, прямо или косвенно вызывает функции,

входящие в Win32 API. Работая на VBA, неявно всегда приходится иметь дело с

функциями Win32 API, только вызов их упрятан в вызываемых VBA функциях или

методах объектов Office. Более подробно с представленными выше элементами

можно ознакомиться в курсе «Основы офисного программирования и язык VBA»

В.А.Биллинга (ИНТУИТ).

109

Глава 4. Модели решения функциональных и

вычислительных задач

4.1. Общие сведения

Модель – это объект или описание объекта, системы для замещения (при

определенных условиях предложениях, гипотезах) одной системы (т.е. оригинала)

другой системой для лучшего изучения оригинала или воспроизведения каких-либо

его свойств. Модель – результат отображения одной структуры (изученной) на

другую (малоизученную). Отображая физическую систему (объект) на

математическую систему (например, математический аппарат уравнений), получим

физико-математическую модель системы или математическую модель физической

системы. Любая модель строится и исследуется при определенных допущениях,

гипотезах, упрощениях.

Моделирование базируется на математической теории подобия, согласно

которой абсолютное подобие может иметь место лишь при замене одного объекта

другим точно таким же. При моделировании большинства систем (за исключением,

возможно, моделирования одних математических структур другими) абсолютное

подобие невозможно, и основная цель моделирования – модель достаточно хорошо

должна отображать функционирование моделируемой системы.

Модели, если отвлечься от областей, сфер их применения, бывают трех типов:

познавательные, прагматические и инструментальные.

Познавательная модель – форма организации и представления знаний,

средство соединения новых и старых знаний. Познавательная модель, как правило,

подгоняется под реальность и является теоретической моделью.

Прагматическая модель – средство организации практических действий,

рабочего представления целей системы для ее управления. Реальность в них

подгоняется под некоторую прагматическую модель. Это, как правило, прикладные

модели.

Инструментальная модель – средство построения, исследования и/или

использования прагматических и/или познавательных моделей.

По способу моделирования модели бывают:

• эмпирические – на основе экспериментальных фактов, зависимостей,

законов;

• теоретические – на основе математических описаний;

• смешанные, полуэмпирические – на основе эмпирических зависимостей и

математических описаний.

Процесс моделирования состоит из трех этапов:

• построение модели;

• исследование и настройка модели;

• использование модели для решения конкретных задач.

Классификацию

моделей проводят по различным критериям. Модель

называется

статической, если среди параметров, участвующих в ее описании, нет

временного параметра. Модель динамическая, если среди ее параметров есть

временной параметр, то есть она отображает систему (процессы в системе) во

времени. Модель дискретная, если она описывает поведение системы только в

110