Хамухин А.А. Введение в информатику для инженеров нефтегазового дела:

Подождите немного. Документ загружается.

дискретные моменты времени. Модель непрерывная, если она описывает

поведение системы для всех моментов времени из некоторого промежутка времени.

Модель детерминированная, если каждому входному набору параметров

соответствует вполне определенный и однозначно определяемый набор выходных

параметров; в противном случае – модель стохастическая (вероятностная).

Основные свойства любой модели:

• целенаправленность – модель всегда отображает некоторую систему, т.е.

имеет цель;

• полнота – в модели должны быть учтены все основные связи и отношения,

необходимые для обеспечения цели моделирования;

• упрощенность – модель отображает только существенные стороны объекта

и, кроме того, должна быть проста для исследования или воспроизведения;

• адекватность – модель должна успешно описывать моделируемую систему;

• информативность – модель должна содержать достаточную информацию о

системе (в рамках гипотез, принятых при построении модели) и должна давать

возможность получить новую информацию;

• управляемость – модель должна иметь хотя бы один параметр, изменениями

которого можно имитировать поведение моделируемой системы в различных

условиях.

4.2. Примеры моделей функциональных и

вычислительных задач в нефтегазовом деле

Модели функциональных и вычислительных задач нефтегазового дела имеют

как общие свойства с моделями, применяемыми в других инженерных дисциплинах,

так и специфические, присущие только для этой предметной области.

Наиболее яркий пример такой специфической модели приведен в главе 1 (3D-

визуализация нефтегазового пласта по данным сейсморазведки). Восстановление

геометрии локальных неоднородностей по наблюдаемому интегральному

акустическому полю относится к классу обратных задач, которые являются

наиболее сложными и однозначного решения не имеют.

Для построения такой модели требуются знания из разных разделов науки:

теории эксперимента, физики колебаний и волн, математического описания

прохождения и отражения акустического сигнала от неоднородностей земной коры,

методов решения систем волновых интегральных и дифференциальных уравнений,

алгоритмов программирования для решения обратных задач.

Такая модель настолько сложна, что ее рассмотрение выходит далеко за рамки

настоящего пособия.

Поэтому рассмотрим ряд примеров функциональных задач нефтегазового

дела, которые необходимо решать с помощью типовых вычислительных методов

(задач) с использованием тех или иных математических моделей, доступных для

понимания при обучении на первом курсе. Освоение этих задач является начальным

и необходимым этапом для изучения в дальнейшем более сложных моделей вплоть

до упомянутой выше задачи 3D-визуализации.

В табл. 4.1 приведены наиболее часто встречающиеся примеры

функциональных задач, которые требуют формулировки соответствующих

вычислительных задач и их модели.

111

Таблица 4.1

Примеры функциональных и вычислительных задач нефтегазового дела

№

п.п.

Функциональная

задача

Вычислительная

задача (метод)

Пример модели

(для практических

занятий)

1 Оцифровка

аналоговых

измерений

Правильный выбор

шага дискретизации и

уровня квантования

аналогового сигнала

Правильный выбор шага

по координате Х и

переменной Y модели

аналогового сигнала

2 Обработка ошибок

измерений,

восстановление

недостающих

данных

Интерполяция,

экстраполяция

По заданным N точкам

«точных» измерений

заменить ошибочные

или недостающие М

точек с помощью

интерполяционной

формулы Лагранжа

3 Сглаживание

экспериментальных

данных

Аппроксимация Моделирование

«зашумленного» ряда

данных и линейная

аппроксимация методом

наименьших квадратов,

квадратичная

аппроксимация

средствами Excel

4 Расчет площадей и

объемов, заданных

координатами

контуров

месторождений

Численное

интегрирование

По координатам

заданной фигуры (с

известной площадью)

вычислить ее площадь с

помощью трех формул

(прямоугольников,

трапеций, Симпсона) и

сравнить их по

погрешности

5 Поиск особых точек

на контурах

месторождений и

иных целевых

функциях

Численное

дифференцирование,

методы

последовательных

приближений

(оптимизации)

Методы

последовательных

приближений

(дихотомии, хорд-

касательных), включая

табуляцию заданной

функции для

визуализации всех ее

корней

112

Окончание табл. 4.1

№

п.п.

Функциональная

задача

Вычислительная

задача (метод)

Пример модели

(для практических

занятий)

6 Статистический

анализ

экспериментальных

данных

Расчет сумм,

произведений,

арифметических

выражений

На примере расчета

коэффициента линейной

регрессии в трех средах

(Excel, VBA, MathCAD)

7 Перевод

экспериментальных

данных из одних

единиц измерения в

другие

Организация

циклических

расчетов с

арифметическими

выражениями

Пересчет химического

состава пластовой нефти

из % мольных в

% массовые, тонны,

баррели и кубометры

для жидкой и газовой

фаз

8 Моделирование

процессов

переработки нефти

Численное решение

систем

обыкновенных

дифференциальных

уравнений (методы

Эйлера, Рунге-Кутта)

Решение системы из

трех дифференциальных

уравнений методом

простой итерации (метод

Эйлера) для типовых

преобразований веществ

В следующих разделах эти задачи рассмотрены подробнее.

4.3. Оцифровка аналоговых измерений

Первым этапом получения информации является процесс измерения

интересующих нас величин. Если наблюдаемая (измеряемая) величина

распределена в пространстве (и/или во времени), то еще до начала измерений

необходимо решить вопрос: сколько делать измерений по каждой координате, с

каким шагом, с какой точностью измерять. Все эти вопросы рассматриваются в

теории измерений, но и в информатике имеется похожая задача, которая возникает

при оцифровке некоторых данных, заданных графически (или аналитически).

Естественный ответ на вопрос, сформулированный выше: «Чем больше берем точек

для оцифровки, тем лучше». Однако существуют технические ограничения по

объему имеющейся в распоряжении памяти, по скорости обработки данных,

поэтому важно знать, на сколько теоретически можно уменьшать это количество.

Фундаментальный подход к решению этой задачи сформулирован в теореме

Шеннона–Котельникова, которая будет сформулирована ниже. Предварительно

рассмотрим пример оцифровки некоторой величины (сигнала), распределенной по

одной координате, в качестве которой возьмем время, хотя в общем случае это

могут быть и пространственные координаты.

Сигнал, несущий информацию о некоторой измеряемой величине называется

аналоговым, если он представлен в виде другой подобной ей величины (например,

измеряемая величина высоты представляется в виде отклонения стрелки прибора).

113

Сигнал, несущий информацию о некоторой измеряемой величине, называется

цифровым, если он представлен в виде последовательности чисел (или одного

числа), отображающей значения наблюдаемой величины (например, та же высота,

представленная в цифровом приборе).

Преобразование аналогового сигнала в цифровой сигнал называется

оцифровкой, или аналогово-цифровым преобразованием, которое может быть

выполнено автоматически с помощью специального устройства, называемого

аналогово-цифровым преобразователем (АЦП). На рис. 4.1а представлен один из

множества возможных видов аналогового сигнала X, изменяющегося с течением

времени t.

Рис. 4.1а. Пример аналогового сигнала

На первом этапе аналоговый сигнал преобразуется в сигнал, разделённый по

времени, посредством периодической выборки (рис. 4.1б). Временной интервал

между двумя выборками называется периодом выборки, а его обратная величина

называется частотой дискретизации. Согласно теореме о дискретном представлении

(теорема Шеннона–Котельникова), частота дискретизации должна быть, по

крайней мере, в два раза больше наивысшей частоты сигнала. В противном случае

такой сигнал не может быть однозначно восстановлен из выборки. Возникает

вопрос – а как определить эту «наивысшую частоту сигнала»? Для этого

необходимо выполнить частотный анализ сигнала, с помощью, например,

преобразования Фурье, рассмотрение которого выходит за рамки настоящего

пособия [13].

Рис. 4.1б. Временная дискретизация аналогового сигнала

114

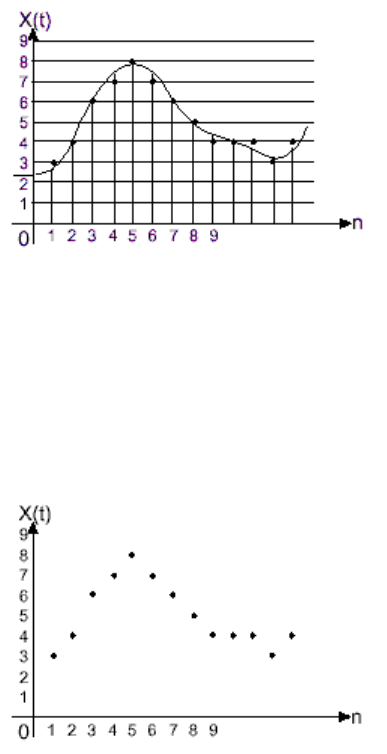
Квантованием называется определение цифровых значений, соответствующих

аналоговым выборкам, взятым на частоте дискретизации. Аналоговый сигнал

квантуется путём приписывания аналоговой величине ближайшего «допустимого»

цифрового значения (рис. 4.1в). Количество цифровых значений называется

разрешением и всегда ограничивается. Например, 256 значений для 8-битного

цифрового сигнала или 10 значений в этом примере. Поэтому квантование

аналоговых сигналов всегда приводит к потере информации. Эта «ошибка

квантования» обратно пропорциональна разрешению цифрового сигнала. Она

также обратно пропорциональна динамическому диапазону сигнала, т.е. интервалу

между минимальным и максимальным значениями (3 и 8 в этом примере).

Рис.4.1в. Дискретизированный и квантованный сигнал

На рис. 4.1г показан результат оцифровки: цифровые значения, которые

соответствуют аналоговому сигналу. Эти значения сняты с выхода АЦП и обычно

представляются в одном из существующих цифровых форматов или в форме

таблицы.

Рис. 4.1г. Оцифрованный сигнал

Итак, все необходимые величины измерены, данные оцифрованы и введены в

компьютер.

Прежде чем начинать анализ данных и извлекать из них ценную информацию

предстоит выявить и обработать погрешности, внесенные на этапе измерения и

оцифровки.

115

4.4. Обработка ошибок измерений, восстановление

недостающих данных

Все измерительные приборы имеют некоторый класс точности, поэтому все

данные измеряются с некоторой погрешностью, которая при передаче может

усиливаться случайным образом из-за помех. Кроме того, возможны просто грубые

ошибки при проведении измерений в силу разных обстоятельств, например, из-за

человеческого фактора или использования неисправного прибора. А в некоторых

значениях координат искомую величину просто невозможно измерить, например,

из-за недоступности (болото, водоём, дикие животные и т.п.). Восстановление

недостающих данных в экспериментальных рядах можно приравнять к задаче

замены грубых ошибочных данных.

Подобные задачи решаются расчетным путем с помощью методов

интерполяции, которые неразрывно связаны с методами аппроксимации.

Математическую основу для решения задач в этой области дает теорема

Вейерштрасса, которая гласит, что любую непрерывную функцию на заданном

интервале всегда можно аппроксимировать полиномом некоторой степени, причем,

чем выше степень полинома, тем меньше будет погрешность аппроксимации.

Другая теорема в этой области гласит, что построения полинома n-ой степени

требуется не менее n+1 заданных точек (пар координата-значение искомой

величины).

Аппроксимацией (приближением) функции f(x) называется нахождение такой

функции g(x) (аппроксимирующей функции), которая была бы близка заданной.

Критерии близости функций f(x) и g(x) могут быть различные.

В том случае, когда приближение строится на дискретном наборе точек,

аппроксимацию называют точечной или дискретной.

В том случае, когда аппроксимация проводится на непрерывном множестве

точек (отрезке), аппроксимация называется непрерывной или интегральной.

Примером такой аппроксимации может служить разложение функции в ряд

Тейлора, то есть замена некоторой функции степенным многочленом.

Наиболее часто встречающим видом точечной аппроксимации является

интерполяция (в широком смысле). Пусть задан дискретный набор точек x

(i=0,1,…n), называемых узлами интерполяции, причем среди этих точек нет

совпадающих, а также значения функции y

в этих точках. Требуется построить

функцию g(x), проходящую через все заданные узлы. Таким образом, критерием

близости функции является g(x

)=y

В качестве функции g(x) обычно выбирается полином, который называют

интерполяционным полиномом. В том случае, когда полином един для всей

области интерполяции, говорят, что интерполяция глобальная. В тех случаях, когда

между различными узлами полиномы различны, говорят о кусочной или

локальной интерполяции.

Найдя интерполяционный полином, мы можем вычислить значения функции

f(x) между узлами (провести интерполяцию в узком смысле слова), а также

определить значение функции f(x) даже за пределами заданного интервала (провести

экстраполяцию). Следует иметь в виду, что точность экстраполяции обычно

невелика и снижается при удалении от заданного интервала измерений.

116

4.4.1 Локальная интерполяция

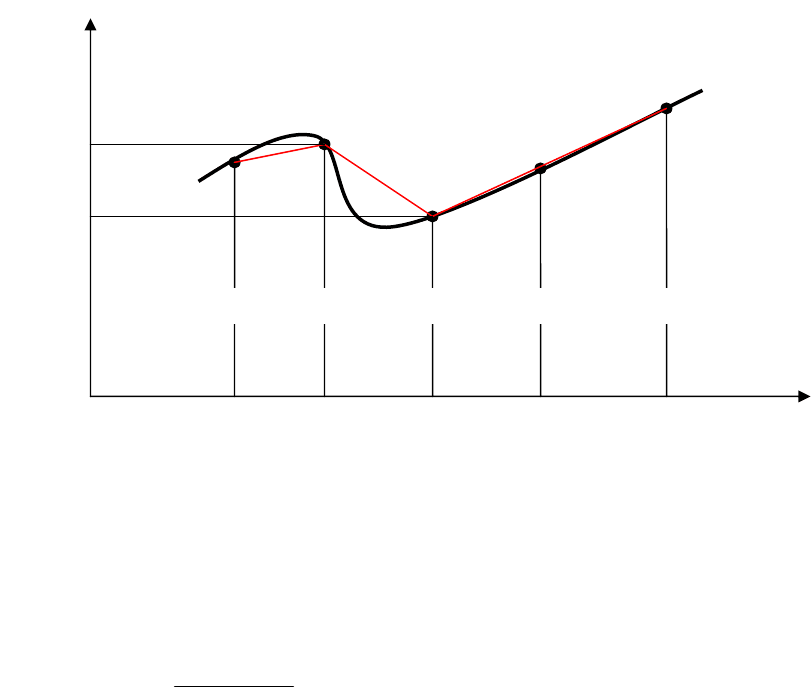
Самым простым случаем локальной интерполяции является линейная

интерполяция, когда в качестве интерполяционной функции выбирается полином

первой степени. При этом узловые точки соединяются прямой линией (рис. 4.2).

Такая интерполяция, когда вместо одной прямой линии используется несколько

отрезков прямых линий (на рисунке – три), называется кусочно-линейной.

Очевидно, что погрешность интерполяции будет тем меньше, чем больше будет

таких отрезков.

Исходная

функция

Узлы инте

поляции

Интерполяционные

функции (прямые)

i-1

Рис.4.2. Пример локальной линейной интерполяции

При линейной интерполяции используется полином 1-й степени, стало быть, для

его построения необходимо знать 2 точки (узла интерполяции):

(

)(

−

YXY

)

. (4.1)

Линейная интерполяция самая простая и имеет самую большую погрешность,

однако часто используется на практике, поскольку если шаг выбрать достаточно

малым, то влияние погрешности можно снизить. На практике также используется

интерполяция полиномом более высокого порядка, например, квадратичная

интерполяция. Расчетные формулы для коэффициентов имеют громоздкий вид,

поэтому их целесообразно представить в матричном виде (4.2), а значение в

промежутках между узлами интерполяции рассчитывается по формуле (4.3):

117

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

; (4.2)

cbXaXXY ++=

)(

. (4.3)

В настоящее время среди методов локальной интерполяции наибольшее

распространение получила интерполяция сплайнами (от английского слова

spline – гибкая линейка). При этом строится интерполяционный полином третьей

степени, проходящий через все заданные узлы и имеющий непрерывные первую и

вторую производные. На каждом интервале [x

i+1

] интерполирующая функция

является полиномом третьей степени:

3)(

2)(

)(

)()()()()(

xxaxxaxxaaxSxS −+−+−+==

(4.4)

и удовлетворяет условиям

yxS =)(

. (4.5)

Если всего n узлов, то интервалов – (n–1). Значит, требуется определить 4(n-1)

неизвестных коэффициентов полиномов. Условие дает нам n уравнений. Условие

непрерывности функции и ее первых двух производных во внутренних узлах

интервала дает дополнительно 3(n-2) уравнений:

).()(

);()(

111

+++

llll

xSxS

(4.6)

Всего имеем (4n–6) различных уравнений. Два недостающих уравнения можно

получить, задавая условия на краях интервала. В частности, можно потребовать

нулевой кривизны функции на краях интервала, то есть:

.0)()(

''''

== bSaS

(4.7)

Задавая различные условия на концах интервала, можно получить разные

сплайны.

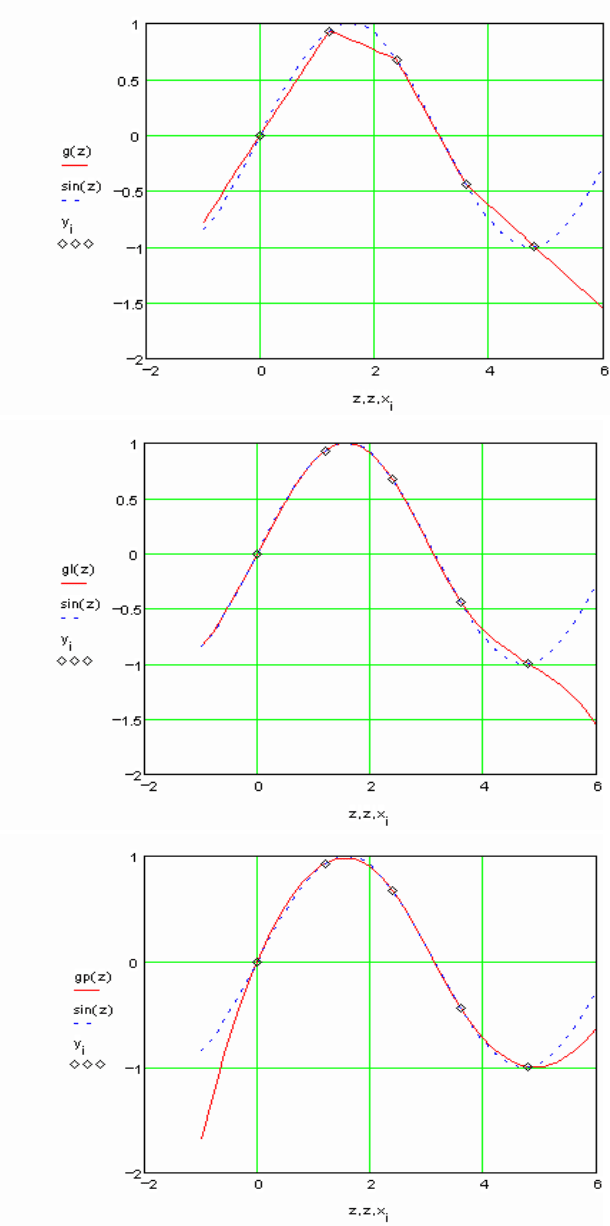
Рассмотрим пример интерполяции синуса с помощью сплайнов (рис.4.3, а-в).

118

Рис. 4.3. Примеры интерполяции части синусоиды (пунктир) сплайнами разного вида (сплошная

линия): а – линейные функции, б – квадратичные функции, в – кубические сплайны

119

Обратите внимание, что результаты интерполяции различными типами

кубических сплайнов практически не отличаются во внутренних точках интервала и

совпадают с точными значениями функции. Вблизи краев интервала отличие

становится более заметным, а при экстраполяции за пределы заданного интервала

различные типы сплайнов дают существенно разные результаты (примеры взяты из

описания применения численных методов Ю.Ю.Тарасевича на сайте

http://www.exponenta.ru/educat/systemat/tarasevich/default.asp).

4.4.2. Глобальная интерполяция

При глобальной интерполяции ищется единый полином для всего интервала.

Если среди узлов {x

, y

} (i=0, 1, … , n) нет совпадающих, то такой полином будет

единственным, и его степень не будет превышать n (теорема Вейерштрасса).

На практике для инженерных расчетов наиболее удобно использовать

интерполяционную формулу Лагранжа. Она не требует предварительного

вычисления коэффициентов полинома, а позволяет сразу вычислять искомое

значение функции Y(X) по N заданным узловым точкам {Xi, Yi}. В модельной задаче,

рассматриваемой на лабораторной работе, ответы (Y

точное

) заранее известны, для

того, чтобы Вы могли рассчитать погрешность интерполяции

и по ней сделать

вывод.

;

)(

*)()(

Точное

расчетнточное

xYxY

−

∏

∑

≠

(4.8)

(4.9)

Фрагмент программы VBA для расчета по формуле Лагранжа при глобальной

интерполяции в случае, когда все точки заданы парами чисел в массивах X и Y:

S = 0

For i = 1 To N

p = 1

For j = 1 To N

If j <> i And j <> Nz Then p = p * ((X(Nz) – X(j)) / (X(i) – X(j)))

Next j

If i <> Nz Then S = S + Y(i) * p

Next i

Y(Nz) = S

Где N – это общее количество точек в ряде экспериментальных данных, Nz –

номер дефектной точки, которая рассчитывается по интерполяционной формуле

120