Hammond C. The Basics of Crystallography and Diffraction

Подождите немного. Документ загружается.

24 Crystals and crystal structures

AAA

Fig. 1.19. On deformation, a B layer atom glides not in a straight line, e.g. B → B (left to right) but

in two steps via a C site across the ‘saddle points’ between the underlying A layer atoms, i.e. B → C

(ﬁrst step), C → B (second step).

(a) (b)

Fig. 1.20. (a)-(d) the sequence of faulting in a ccp (or fcc) crystal which leads to the formation of

a twinned crystal as in Fig. 1.18. In Fig. 1.20(a) the close-packed layer to be faulted is an ‘A’ layer

(arrowed) which in Fig. 1.20(b) becomes a ‘B’layer and the layers above are relabelled accordingly; then

the next layer above (the ‘C’ layer, arrowed) is faulted to become an ‘A’ layer (Fig. 1.20(c)) and so on.

for the generation of a twinned crystal by deformation is illustrated sequentially in

Fig. 1.20. Figure 1.20(a) shows the close packed layers of a single fcc crystal ‘edge

on’. Let us now slip an A layer (arrowed) into the sites of the B layer atoms (partial

slip), as shown in Fig. 1.20(b). In doing so all the layers above the A layer move too:

B → C; C → A; A → B and so on. Figure 1.20(b) also shows these re-labelled lay-

ers of atoms. Now let us slip the next layer up (arrowed), C → A; and again A → B,

B → C and so on (Fig. 1.20(c)). Again, slip the third layer up (arrowed) and re-label

the layers—as shown in Fig. 1.20(d). As we can see we will ultimately generate the

1.9 Stacking faults and twins 25

twinned crystal as shown in Fig. 1.18. This mechanism for deformation-twin formation

may appear to be complicated; it occurs in practice (as in nearly all material deformation

processes) through the movement of (partial) dislocations, a subject of great importance

in materials science. The arrows in Fig. 1.19 represent the slip vectors for dislocations

passing through the crystal; a slip vector such as B→B, in which the stacking sequence

is unchanged, represents the passage of a whole dislocation; a slip vector such as B→C

or C→B in which, as described above, the stacking sequence is changed, represents

the passage of a partial dislocation. Such whole and partial dislocations also occur in

bcc metal (and other) crystals. In the particular example above (Fig. 1.19) the partial

dislocation vectors B → C and C → B (which lie in the close-packed slip plane) are

called Shockley partials, after William Shockley

∗

who ﬁrst identiﬁed them.

The twinned crystal shown diagrammatically in Fig. 1.18 is just one particular exam-

ple of very general phenomenon, which occurs in crystals with much more complex

structures and in which the two parts of the twinned crystal may not simply be related by

reﬂection across the twin plane (reﬂection twins). In general a twinned crystal is one in

which the two parts are related to each other by a rotation (usually, but not necessarily,

180˚) about some particular direction called a twin axis. For example, we could create

the twinned crystal in Fig. 1.18 by folding the ﬁgure 180˚ along the dashed line (the

twin axis) which lies in the twin plane; alternatively we could ‘cut’ the single crystal in

Fig. 1.20(a) in two along the c layer and create the twinned crystal by rotating the upper

half 180˚ about a vertical direction (another twin axis) which in this case is normal to

the twin plane. In our crystal all these actions (reﬂection in the twin plane, rotation 180˚

about an axis in the twin plane, rotation 180˚ about an axis normal to the twin plane)

are all equivalent, but this is not necessarily the case as we will discover when we have

learned about the symmetry of crystals.

Some examples of twinned crystals from geology and metallurgy are shown in Fig.

1.21. The left–right-hand character of the twinned crystal in Fig. 1.21(a) is easily seen;

in practice the twins may be interpenetrated and twinning may occur not just in one

but in several different planes, as shown in Figs 1.21(b) and (c). In metals and alloys,

the presence of twins may be seen in polished and etched surfaces (Fig. 1.21(d)). Old

cast brass doorknobs provide a good and homely example. The stacking fault energy of

α-brass (Cu ∼ 30% Zn) is very low (30 mJ m

−2

) and almost all the grains or crystals

will contain twins. The corrosive contact of human hands reveals the irregular outlines

or boundaries between the grains and also the perfectly straight lines or traces of the

twin boundaries which terminate (unlike scratches) at the grain boundaries, as shown in

Fig. 1.21(d).

Twinning is very common in minerals, frequently occurring as a result of phase

transitions during cooling. They may be observed, like the brass, on the polished surfaces

of minerals, where they may give rise to beautiful iridescent textures as a result of the

diffraction and interference of light (Chapter 7). They may be more readily seen in

petrographic thin sections under the polarizing light microscope. For the petrologist

they constitute one of the most important means of mineral identiﬁcation.

∗

Denotes biographical notes available in Appendix 3.

26 Crystals and crystal structures

(b)(a)

(c)

(d)

Fig. 1.21. Examples of twinned crystals: (a) rutile (TiO

) twinned on a {101} plane (from Rutley’s

Elements of Mineralogy, 25th edn, revised by H. H. Read, George Allen and Unwin Ltd, 1962); (b)

multiple twinning in rutile (from Introduction to Crystallography, 3rd edn, by F. C. Phillips, Longmans,

1963); (c) interpenetrant twin in mercurous chloride (HgC1), twin plane {101} (from F. C. Phillips loc.

cit); (d) a photomicrograph ofthe etched surface ofα-brassshowing grainboundaries and (straight-sided)

annealing twins, twin plane {111}.

1.10 The crystal chemistry of inorganic compounds

The newcomer to crystallography is often dismayed by the daunting level of complexity,

or immensity of all the different crystal structures—not only inorganic but also organic.

The subject may seem to depend so much on rote-learning and the committing to memory

of a vast number of facts. The subject is certainly immense, but it is not arbitrary, and the

1.10 The crystal chemistry of inorganic compounds 27

rules or criteria determining the simplest structures described in the preceding sections

are the stepping-stones to an understanding of more complex structures.

We will consider the types of bonding which apply to inorganic crystals and the main

differences to organic crystals (which are considered in more detail in Chapter 4). We

have already seen how crystals may be represented as plans or projections (Section 1.8):

now we will see how they can be represented in terms of coordination polyhedra, which

lead naturally to a (brief) discussion of Pauling’s rules which describe the conditions

for the stability (and therefore the existence of) predominantly ionic crystal structures.

Then, in Section 1.11, we describe some rather more complex crystal structures which

either illustrate the principles we have already learned or for their own intrinsic interest

and topicality.

1.10.1 Bonding in inorganic crystals

So far in this book we have described some simple crystal structures solely in geometrical

terms—i.e. the various arrangements in which ions and atoms of different sizes can pack

together. Now we must consider the forces which hold the ions and atoms together. This

is of course a subject of profound importance in physical chemistry and we can only

summarize, in a very simple way, the main features of the bonding mechanisms.

In inorganic crystals, the dominant bonding forces are ionic or heteropolar bonds

and covalent or homopolar bonds, with lesser contributions from van der Waals and

hydrogen bonds.

Ionic bonding dominates in inorganic crystals as a result of the high electronegativity

difference between the atomic species—the (positive) metal cations on the one hand

and the (negative) F

−

,Cl

−

2−

anions on the other. The simple compounds NaCl,

CsCl and CaF

which we have already described are examples of almost ‘pure’ ionic

bonding. Moreover, the ionic bond is non-directional, an important characteristic which

it shares with the metallic bond which is the dominant cohesive force in metals with

a high conductivity: the positive metal ions are held together by a ‘sea’ of conduction

electrons which are wholly non-localized, i.e. the electrons are not bound to individual

atoms.

As the electronegativity difference between the atomic species decreases, the covalent

bond begins to dominate: the bonding electrons are ‘shared’between the atoms instead of

being transferredbetween the atomic orbitals. In sulphides, e.g. ZnS, thebonding is partly

covalent. Unlike the ionicbond, the covalentbond is directional, the conﬁguration around

the atoms corresponds to, or arises from, the conﬁguration of the atomic orbitals. An

example of‘pure’covalent bondingis diamond (thehardest material known), described in

more detail in Section1.11.6. The carbon atomsindiamond are tetrahedrally coordinated,

corresponding to the pattern of the sp

orbitals. The metallic bond, mentioned above,

may be regarded as a ‘special case’ of a covalent bond—an atom shares electrons with

its nearest neighbours and the empty orbitals permit the ﬂow of conduction electrons.

In many inorganic compounds, the bonding is a ‘mixture’ of (dominantly) ionic and

(dominantly) covalent bonding. For example, in calcite, CaCO

, the bonding between

the Ca

and (CO

)

2−

ions is dominantly ionic but the bonds which hold the (CO

)

2−

groups together is dominantly covalent. The structure of calcite strongly resembles that

28 Crystals and crystal structures

: Ca; : O

Fig. 1.22. The rhombohedral structure of calcite, CaCO

. The cell shown is not the smallest unit cell

but corresponds to the cleavage rhombohedra which occur in natural crystals of calcite. The smallest

unit cell may be outlined by linking together the eight innermost Ca

ions, following the pattern shown

in Figure 1.7(c). (From An Introduction to Crystal Chemistry, 2nd Edn, by R. C. Evans, Cambridge

University Press, 1964.)

of NaCl, except that the presence of the planar (CO

)

2−

groups, all orientated the same

way, parallel to the ABCABC … stacking sequence (see Fig. 1.6(b)), ‘distorts’the cubic

symmetry, or shape of the unit cell, to rhombohedral as shown in Fig. 1.22.

It is the high strength of ionic and covalent bonds which gives rise to the most char-

acteristic mechanical property of inorganic compounds—their high hardness. However,

many inorganic compounds are highly anisotropic in their mechanical properties, being

‘strong’in some directions and ‘weak’ in others. Examples are the ‘layer-structure’phyl-

losilicates, talc and mica (see Section 1.11.4) and graphite (see Section 1.11.6). Within

the layers the ions/atoms are strongly ionically or covalently bonded, but the layers are

only held together by much weaker van der Waals bonds which arise from the contin-

uously changing dipole moments within atoms or molecules. An analogous situation

applies to solid organic compounds; the atoms in the molecules themselves are strongly

covalently bonded but the molecules are held together by weak van der Waals bonds and

solid organic compounds are, in comparison, generally soft materials.

The concept of a molecule, introduced above, is of course fundamental in chemistry,

but it can be an obstacle in understanding the arrangements and proportions of atoms

and ions in inorganic compounds in the solid state. For example, it is not possible to

identify a ‘molecule’ of NaCl in a crystal (Fig. 1.14(a)); each Na ion is bonded equally

to six surrounding Cl ions and vice versa; the Na and Cl ions are not ‘paired’ to each

other in any special way. W. L. Bragg records (in The Development of X-ray Analysis)

that his chemical colleagues were loath to give up the idea of molecules in inorganic

compounds and even as late as 1927, Henry E.Armstrong, an eminent chemist, published

the following letter in Nature.

1.10 The crystal chemistry of inorganic compounds 29

‘Poor Common Salt’

“Some books are lies frae to end” says Burns. Scientiﬁc (save the mark) speculation would seem

to be on the way to this state!... Prof. W.L. Bragg asserts that “In sodium chloride there appear to

be no molecules represented by NaCl. The equality in number of sodium and chlorine atoms is

arrived at by a chess-board pattern of these atoms; it is a result of geometry and not of a pairing-off

of the atoms.”

This statement is more than repugnant to common sense. It is absurd to the n..th degree, not

chemical cricket. Chemistry is neither chess nor geometry, whatever X-ray physics may be. Such

unjustiﬁed aspersion of the molecular character of our most necessary condiment must not be

allowed any longer to pass unchallenged … It were time that chemists took charge of chemistry

once more and protected neophytes against the worship of false gods; at least taught them to ask

for something more than chess-board evidence.

However, perhaps the letter was written with a pinch of salt!

In addition, many inorganic compounds are non-stoichiometric. FeO, for example,

which has the same structure as NaCl, rarely has the exact formula FeO, but a smaller

proportion of Fe than in the ratio 1:1. This simply indicates the existence of vacant Fe

lattice sites and equal numbers of Fe

ions on other sites to ensure electrical neutrality

and does not indicate a distinct chemical compound (see Section 1.11.3).

However, as mentioned above, the concept of a molecule is of vital importance

in understanding the structures of solid organic compounds. The strong covalent bonds

which bindtogether the carbon, nitrogen, oxygen, etc. atoms within theorganic molecule,

and which cause it to retain its identity when the compound is melted, dissolved, or even

vaporized, are much stronger than the van der Waals bonds between the molecules

in the solid state. The symmetries of the crystal structures which occur are, to a ﬁrst

approximation, determined by the overall shape or envelope of the molecules and the

ways in which they pack together in the most efﬁcient manner. However, we defer any

further consideration of organic compounds until Chapter 4 when we have learned about

symmetry, lattices and the methods needed to describe the geometry of crystals.

1.10.2 Representing crystals in terms of coordination polyhedra

As we have seen in Sections 1.6 and 1.7, inorganic crystal structures may be described in

terms of (small) atoms or cations, surrounded, or coordinated by, (large) atoms or anions.

An alternative and very fruitful way of representing such structures is to concentrate

attention on the coordinating polyhedra themselves rather than the individual atoms

situated at their corners. We can then view the crystal structure as a pattern of linked

polyhedra, without our view being obscured, as it were, by the large atoms or ions

themselves.

The most important coordination polyhedra in inorganic crystals are the tetrahedron,

= 0.225; the octahedron, r

= 0.414 (see Section 1.6) and the cubeoctahe-

dron and hexagonal cubeoctahedron, r

= 1.000, all of which occur in close-packed

See Appendix 2 – Polyhedra in crystallography.

30 Crystals and crystal structures

structures. The last two polyhedra represent the pattern of 12 atoms surrounding, or

co-ordinating, an atom in face-centred and hexagonal close-packing respectively.

The polyhedra may be separate or linked together in various ways – corner-to-corner,

edge-to-edge, face-to-face or in various combinations. Geometrically, the possibilities

are almost endless, but in terms of the stability of inorganic crystals, they are not. The

criteria which govern the stability, and hence possible structures, in (dominantly) ionic

crystals, were set out by Linus Pauling

∗

in a series of empirical rules. Essentially, these

rules express the requirement for a charge balance between a cation and its surround-

ing polyhedron of anions and also between an anion and the cations that immediately

surround it. The chemical law of valency is satisﬁed not by ‘pairing off’ individual

anions and cations but by a ‘sharing’, or distribution of (say) the positive charge of

a cation among the surrounding polyhedron of anions. This is further evidence of the

(c)

(a) (b)

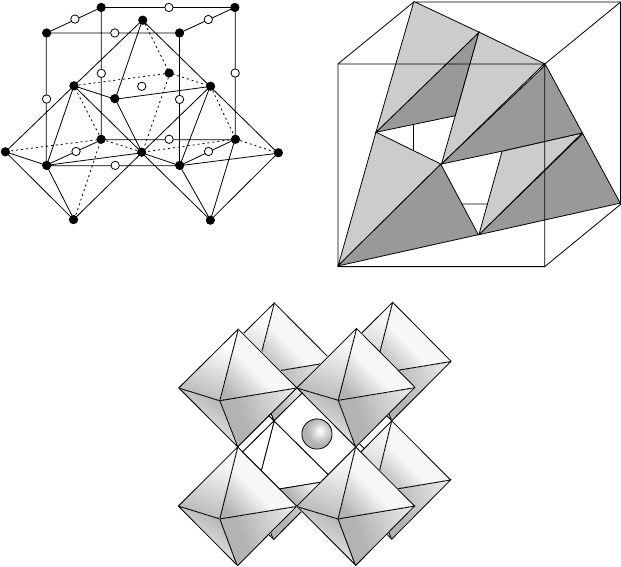
Fig. 1.23. Co-ordination polyhedra in three simple crystal structures: (a) edge-sharing octahedra in

sodium chloride; (b) corner-sharing tetrahedra in zinc blende; and (c) corner-sharing octahedra and the

(central) cubeoctahedron in perovskite. (From An Introduction to Mineral Sciences by Andrew Putnis,

Cambridge University Press, 1992.)

∗

Denotes biographical notes available in Appendix 3.

1.11 Some more complex crystal structures 31

non-existence of identiﬁable ‘molecules’ in inorganic ionic structures. Pauling’s rules

also determine, or limit, the ways in which the polyhedra can be linked together. The

octahedra and cubeoctahedra surrounding larger and weaker cations may share corners,

edges or even faces, but the tetrahedra surrounding the smaller and more highly positive

cations tend only to share corners, such that the cations are as far apart as possible.

We have already encountered this aspect of Pauling’s rules in our discussion (Section

1.7) of the ‘non-existence’ of hcp structures in which all the tetrahedral sites are ﬁlled;

the sites occur in pairs with the tetrahedra arranged face-to-face and the cations are too

close to ensure stability. This also applies to the (Si,Al)O

tetrahedra which comprise the

building blocks of the silicate minerals (see Section 1.11.4), the tetrahedra are isolated

or share one, two, three or four corners, never edges or faces. However, this is not true of

all synthesized ceramic materials. The new nitrido-silicates and sialons are based on the

linkage of (Si, Al)(N, O)

(predominantly SiN

) tetrahedra which share edges as well as

corners and in addition, Si is octahedrally coordinated by N.

Figure 1.23 shows the coordination polyhedra in three simple crystal structures: (a)

the edge-sharing octahedra in sodium chloride, NaCl; (b) the corner-sharing tetrahedra

in zinc blende, ZnS; and (c) the corner-sharing octahedra and the central cubeoctahedron

in perovskite, CaTiO

. The unit cell shown is the same as that in Fig. 1.17(a).

1.11 Introduction to some more complex crystal structures

1.11.1 Perovskite (CaTiO

), barium titanate (BaTiO

) and

related structures

Perovskite is an important ‘type’ mineral (in the same way as sodium chloride, NaCl)

and is the basis of many technologically important synthetic ceramics in which the Ca

is replaced by Ba, Pb, K, Sr, La or Co and the Ti by Sn, Fe, Zr, Ta, Ce or Mn. The

general formula is ABO

(see Fig. 1.17), the A ion being in the large cubeoctahedral

sites and the B ion being in the smaller octahedral sites (Fig. 1.23(c)). In perovskite

itself, A is the divalent ion and B the tetravalent ion. This however is not a necessary

restriction; trivalent ions can, for example, occupy both A and B sites; all that is needed

is an aggregate valency of six to ensure electrical neutrality. It is, in short, a working

out of Pauling’s rules again. Of much greater importance are the sizes of these ions

because they lead, separately or in combination, to different distortions of the cubic cell.

In perovskite itself, the Ca cation is ‘too small’ for the large cubeoctahedral site and so

the surrounding octahedra tilt, in opposite senses relative to one another, to reduce the

size of the cubeoctohedral site. This is shown diagrammatically in Fig. 1.24(a). The unit

cell is now larger, as outlined by the solid lines, the unit cell repeat distance now being

between the similarly oriented octahedra (see Section 2.2). The symmetry is tetragonal,

rather than cubic. The tilts are also slightly out of the plane of the projection which

further reduces the symmetry to orthorhombic (see Chapter 3 for a description of these

non-cubic structures).

In barium titanate, BaTiO

, the Ti cation is ‘too small’for the octahedral site and shifts

slightly off-centre within the octahedron (Fig. 1.24(b)); the cubic unit cell is distorted to

tetragonal. These shifts may occur along any of the three cube-edge directions such that a

32 Crystals and crystal structures

(a) (b)

Fig. 1.24. Two modiﬁcations to the perovskite structure: (a) octahedra tilted in opposite senses, the

cubic cell is outlined by dashed lines and the tetragonal cell by full lines; (b) displacements of the B

cations from the centres of the octahedra resulting in a distortion of the original cubic cell to a tetragonal

unit cell (fulllines). (FromAn Introduction to Mineral Sciences byAndrew Putnis, Cambridge University

Press, 1992.)

Fig. 1.25. A polarized-light micrograph (crossed polars) of a single crystal of barium titanate which

reveals the domains in each of which the tetragonal distortion is in a different cube-edge direction.

single crystal of BaTiO

may be divided into domains; within each domain, the shift is in

the same direction (Fig. 1.25) (the idea of domains is discussed, with respect to ordered

crystals, in Section 9.7). The consequence is that within a crystal (or within a domain)

there is a net movement of charge, resulting in a structure with a dipole moment, and this

spontaneous electrical polarization leads to the property of ferroelectricity which is of

1.11 Some more complex crystal structures 33

such great importance in many electronic devices and is the basis of much research

on the titanates—some of which are antiferroelectric (e.g. PbZrO

), ferromagnetic

(e.g. LaCo

0.2

0.8

) or antiferromagnetic (e.g. LaFeO

). Barium titanate itself under-

goes further transformations at lower temperatures (to orthorhombic and rhombohedral

forms) which are, as with the tetragonal form, ferroelectric.

At higher temperatures (120

◦

C for barium titanate), due to the increased thermal

movement of the atoms, these structures revert to the cubic forms. This is an example

of a displacive transformation: no bonds are broken. Such displacive transformations

also characterize the ‘high temperature’ (α) and ‘low temperature’ (β) forms of quartz,

tridymite and cristobalite (see Section 1.11.5) and also relate the polymorphous forms

of many organic compounds—the structures only differing in the way in which the

molecules are packed together under the inﬂuence of the weak van der Waals forces.

1.11.2 Tetrahedral and octahedral structures—silicon carbide

and alumina

Consider, for example, the crystal structures which consist of close-packed or nearly

close-packed layers of large atoms or ions with the smaller atoms or ions occupy-

ing some or all of the tetrahedral interstitial sites. Zinc blende and wurtzite are two

such structures (Section 1.7) which are re-drawn in Fig. 1.26 so as to emphasize the

B4 (2H)

Wurtzite

c = 2

√2

B3 (3C)

Zinc blende

B5 (4H)

Carborundum III

B6 (6H)

Carborundum II

B7 (15R)

Carborundum I

√3

c = 3

√2

√3

c = 4

√2

√3

c = 6

√2

√3

c = 15

√2

√3

Fig. 1.26. Five common tetrahedral structure types. The bracketed symbols refer to the number of

layers in the repeat sequence and the structure type: H (hexagonal), C (cubic) and R (rhombohedral)

(after E. Parthe, Crystal Chemistry of Tetrahedral Structures, Gordon and Breach, New York, 1964,

reproduced from The Structure of Metals, 3rd edn, C. S. Barrett and T. B. Massalski, Pergamon, 1980).