Халиуллин Р.Н., Сопуев А. Олимпиады по информатике

Подождите немного. Документ загружается.

- 31 -

при тщательном и глубоком анализе условия задачи. Оценка, получаемая

участником олимпиады, зависит от того, сумел ли он их обнаружить и учесть

при составлении алгоритма или программы.

Известно правило, что ни одна, впервые составленная, программа не на-

чинает работать сразу, с первого раза. В программе могут быть допущены

ошибки при ее разработке

, при вводе с клавиатуры, поэтому программу при-

ходится «доводить до ума» уже на компьютере.

Поиск ошибок в сложной программе больше всего напоминает работу

Шерлока Холмса над запутанным делом или охоту на очень хитрого зверя.

Программист по крупицам собирает «улики», выдвигает различные версии

появления ошибки и организует для их проверки «следственные»

экспери-

менты, подстраивает ошибкам ловушку за ловушкой, устраивает на них об-

лавы, идет «по следам», выявляет подозрительные предписания и придумы-

вает для них проверки. Умение программировать заключается в том, чтобы

любую программу «заставить» работать.

РЕШЕНИЕ СОДЕРЖАТЕЛЬНЫХ ЗАДАЧ

Содержательные задачи, обычно на несколько арифметических и ал-

гебраических действий, берутся из задачников по алгебре для 5-6 классов. В

этих задачах требуется найти рабочую формулу, обеспечить ввод и вывод

вычисляемых величин. Исходные данные вводятся либо вместе с текстом

программы (операторы LET, DATA/READ), либо с клавиатуры (оператор

INPUT), а результаты выводятся на экран дисплея

с помощью команды

PRINT. Для примера возьмем задачу с коровами и лошадьми (11 кл., 1997г.).

Задача. Одна корова за сутки съедает A кг сена, одна лошадь – B кг.

Составить программу вычисления наибольшего числа коров, которых мож-

но прокормить совместно с L лошадьми в течение N дней. Сколько сена при

этом останется, если запас сена составляет P кг

Программа или алгоритм решения этой задачи основаны на аналитиче-

ском решении, как на обычном уроке математики, и вывод рабочей формулы

основывается на цепочке рассуждений:

1 лошадь за 1 день съедает В кг сена;

L лошадей за 1 день съедают BL кг сена;

L лошадей за N дней съедают BLN кг сена.

P-BLN – количество сена, предназначенного для кормления К коров в тече-

ние тех же N дней вместе с лошадьми. Учитывая, что одна корова за 1 день

съедает А кг сена, а за N дней она съедает AN кг сена, можно вычислить, на

сколько

коров этого остатка хватит. Это – частное от деления P-BLN на AN

(целая часть дроби): K=int

)(

NLBP

⋅

−

. Может оказаться так, что этого сена

- 32 -

не хватит даже для одной коровы (К=0). В любом случае остаток сена соста-

вит P-BLN-KAN.

Главная особенность решения этой задачи заключается в проверке допусти-

мости вводимых величин и установке реакции машины на разные варианты

исходов задачи. При составлении программы учитываются варианты: а) сена

не хватит для лошадей; б) сена не хватит

коровам; в) сена хватит для К ко-

ров.

10 REM ЛОШАДИ И КОРОВЫ

20 INPUT A, B, L, N

30 INPUT P

40 IF P<L*B*N THEN 30

50 K=INT((P-L*B*N)/(A*N))

60 P=P-L*B*N-K*A*N

70 IF K=0 THEN PRINT “НЕ ОСТАНЕТСЯ КОРОВАМ”:GOTO 90

80 PRINT “ХВАТИТ НА”;K;“КОРОВ”

90 PRINT “ОСТАНЕТСЯ”;P;”КГ СЕНА”

Таким образом, в решении содержательных задач по информатике ха-

рактерно следующее: 1) вывод рабочей формулы; 2) обеспечение безопасно-

сти при вводе; 3) варьирование вывода результата в зависимости от полноты

выполнения условий или имеющихся ограничений;

Многие ограничения вводятся самим программистом, исходя из смысла

и допустимости. Например, нельзя массу или площадь выражать отрицатель-

ным числом или

число предметов выражать дробными числами.

«Подводные камни» в олимпиадных задачах обычно обнаруживаются не

сразу, а в процессе обкатки и тестирования программы. Это могут быть отка-

зы, сбои, зацикливания, разнобой в ответах и так далее. Например, в задаче о

разделе поля на две равные по площади части (10 класс, 1997г.) намеренно

приведен

рисунок, наталкивающий участника на «легкое» решение. Рассмот-

рим подробнее решение этой задачи.

Задача.

Разделить поле на две равные по площа-

ди части с помощью межи, проведенной парал-

лельно стороне b. Все стороны, кроме одной, па-

раллельны или перпендикулярны между собой. Зна-

чения a, b, c даны, причем c<a. Все размеры дают-

ся в метрах.

Все участники олимпиады, которые решали эту задачу, составили про-

грамму, считая, что слева участок всегда

прямоугольный и дали простое ре-

шение:

Полная площадь участка (площадь трапеции) равна

⋅

. Пло-

щадь левой части участка (площадь прямоугольника)

bxS =

, а площадь

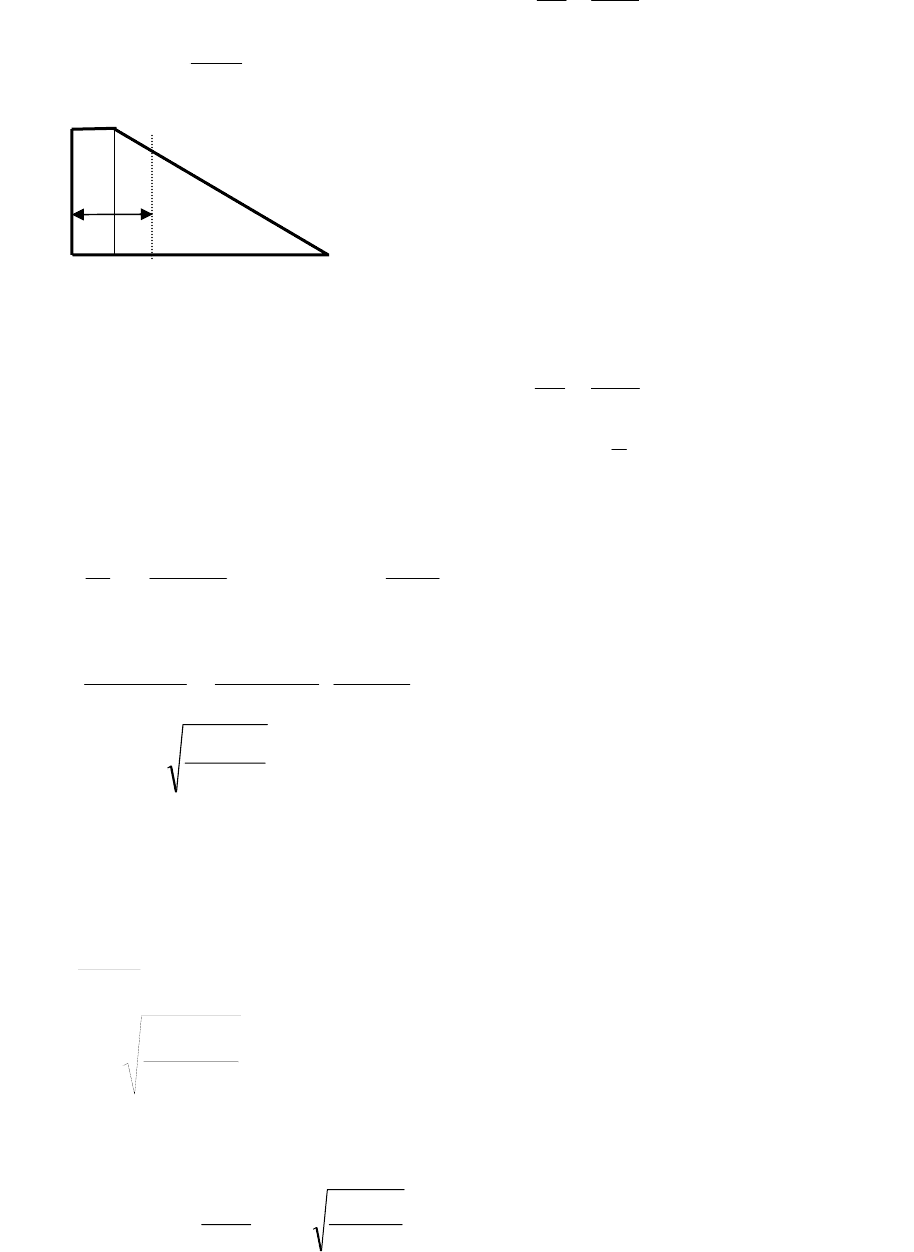
- 33 -

правой части (половина всей площади)

⋅

. Из равенства

следует, что

. Этому решению соответствует программа:

Однако поле может иметь другую форму, в этом случае межа проходит

по треугольной части поля (см. рисунок). Тогда площадь левой части опреде-

ляют как половину всей площади поля

⋅

, а правой части - как

площадь прямоугольного треугольника MDN:

hxaS ⋅−⋅= )(

, где h – высота

треугольника, которую можно определить из подобия треугольников MDN и

CDE:

−

, откуда

h ⋅

−

Подставив значения S

и S

в равенство

можно найти x:

)()(

)( xa

bxabca

−

⋅

−

⋅−

⋅+

→

222

)(2 xaca −⋅=−

откуда

−

−=

. Соответствую-

щая программа может быть записана так:

С учетом обоих случаев, рабочая формула должна иметь ветвление:

Переход от одной рабочей формулы к другой происходит при соблю-

дении условия:

ca −

−=

, откуда следует a=3c.

10 INPUT A,B,C

20 IF C<A THEN 10

30 X=A-SQR((A^2-C^2)/2)

40 PRINT “X=”;X

10 INPUT A,B,C

20 IF C<A THEN 10

30 X=(A+C)/4

40 PRINT “X=”;X

50 END

⎪

⎩

⎪

⎨

⎧

−

≤

c3a если ,

сa

c3a если ,

10 INPUT A,B,C

20 IF C<A THEN 10

30 IF A<=3∗C THEN X=(A+C)/4

ELSE X=A-SQR((A^2-

C^2)/2)

40 PRINT “X=”; X

- 34 -

Численное решение осуществ-

ляется в виде цикла, путем постепен-

ного перемещения межи слева напра-

во с малым шагом, например

dx=0,001. При каждом шаге произво-

дится вычисление x=x+dx и S=S+dS.

Шаг за шагом значение S растет и

цикл нужно прекратить, как только

выполнится условие S≥S

Точность определения положе-

ния межи зависит от величины шага

цикла dx. Например, шаг dx=0.01

обеспечивает точность ±1 см.

Задача о грузчиках (11 класс, 1999 г.)

Бригада грузчиков может за один рабочий день (с 8.00 до 16.00) может раз-

грузить 6 вагонов. Ежедневно к началу смены на разгрузку подается от 3 до

9 вагонов. В субботу бригада не

уходит с работы до тех пор, пока не будет

разгружен последний вагон. В какое время в субботу грузчики закончат ра-

боту?

Решение задачи основано на компьютерном моделировании подачи ва-

гонов на разгрузку с помощью генератора случайных чисел. Ежедневную по-

дачу от 3 до 9 вагонов можно моделировать выражением N=int(rnd(1)·(9-

3+1))+3=int(rnd(1)·7)+3. Если на один

день выпадает более 6 вагонов (N>6),

то разгрузка части вагонов переносится на следующий день.

Ошибочное решение заключается в суммировании числа вагонов за не-

делю, определении «лишних» вагонов и вычисление времени выполнения

работы досрочно или с запозданием. От общего числа вагонов вычитают

число вагонов, которые грузчики могут разгрузить за 6 дней (6 дней по 6

ва-

гонов = 36 вагонов). Если разность будет отрицательной, то грузчики закон-

чат работу до 16.00 часов. Если разность положительная, то добавочное вре-

мя нужно прибавить к 16.00.

На самом деле, задачу нужно решать последовательно, день за днем. В

первые 5 дней грузчики могут работать даже неполный день, но, если подано

более 6 вагонов, то разгрузка вагонов

, оставшихся неразгруженными до

16.00, переносится на следующий день. Неразгруженные вагоны могут нака-

пливаться в течение недели, и может случиться так, что грузчикам придется

работать и в воскресенье.

Тело цикла состоит из следующих действий: к числу поданных под

разгрузку вагонов прибавить число вагонов, оставшихся в предыдущий день;

если число вагонов превышает 6, то

разгрузка лишних вагонов переносится

на следующий день. По окончании цикла, если число вагонов на субботу

30 X=0:S=0:H1=B:DX=0.01

40 S0=(A+C)/2∗B

50 X=X+DX

60 IF X<=C THEN GOSUB 110

ELSE GOSUB 130

70 S=S+DS

80 IF S<S0/2 THEN 50

90 PRINT “X=”;X

100 END

110 S=B∗DX

120 RETURN

130 H=B/(A-C)∗(A-X)

140 DS=(H1+H)/2∗DX

150 H1=H

160 RETURN

- 35 -

меньше 6, то вычисляется время окончания до 16.00, а если больше, то к

16.00 прибавляется время разгрузки оставшихся вагонов.

Введем обозначения: T1 и T2 – время начала и окончания работы,

NMIN, NMAX – минимальное и максимальное число подаваемых под разгруз-

ку вагонов в один день, TR – время разгрузки одного вагона, N0, DN – днев-

ная норма

грузчиков и остаток вагонов на следующий день

Обратите внимание на вычисление времени окончания работы в суббо-

ту: DN имеет положительное значение, если есть лишние вагоны, и отрица-

тельное значение, если в субботу разгружают меньше 6 вагонов, поэтому ве-

личина T = T2 ∗ 60 + DN ∗ TR дает время окончания работы в минутах. Что-

бы сделать вывод в формате «час.мин» использованы функции обработки чи-

сел – int(y) и y mod x.

Задача о покупке носков (11 класс, 1992 г.). Одна пара носков стоит

1.05$, дюжина носков стоит 10.25$, а дюжина дюжин – 114$. Требуется

купить не менее N пар носков, заплатив как можно меньше долларов. На-

пример, при N=11 пар дешевле купить дюжину. Дюжина –

это число 12.

Само условие задачи подсказывает, что самая удачная покупка, если

покупать носки «дюжинами дюжин», то есть упакованными по 144 пары нос-

ков. Если это не удается, то часть покупки придется сделать «дюжинами» (в

упаковках по 12), и только в последнюю очередь покупать носки поштучно.

Оплата за носки состоит из трех сумм: S=SDD+SD+SP, где

SDD – стоимость

носков, купленных дюжинами дюжин пар, SD – носков, купленных

дюжинами пар и SP – носков, купленных просто парами.

Решение задачи заключается в следующем: Вначале вводят число N

(общее число пар носков, которые следует купить), затем это число делят на

144 и частное от деления умножают на 114 – это SDD. Полученный остаток

делят на 12 и частное умножают

на 10.25 – это SD. Остаток умножают на

1.05 – это SP.

Полученное решение S=SDD+SD+SP может оказаться неоптимальным,

тогда этот ответ надо сравнить с покупкой на дюжину больше, то есть с

SDD+SD+10.25 и на дюжину дюжин больше, то есть с SDD+114. В зависи-

10 REM РАЗГРУЗКА ВАГОНОВ

20 INPUT T1, T2, N0, NMIN, NMAX

30 TR=(T2-T1)∗60/N0

40 DN=0

50 FOR I=1 TO 6

60 IF DN<0 THEN DN=0

70 N=INT(RND(1)∗(NMAX-NMIN+1))+NMIN+DN

80 DN=N-N0

90 NEXT I

100 T=T2∗60+DN∗TR

110 PRINT INT(T/60);".";T MOD 60

120 END

- 36 -

мости от того, какая из сумм окажется меньше, принимается соответствую-

щее решение.

Здесь нужно обратить внимание на несколько тонкостей: во-первых, в случае

увеличения числа дюжин пар на единицу нужно число пар приравнять нулю,

а во-вторых, учесть, что число пар может достигнуть дюжины пар и

тогда

нужно увеличить число дюжин дюжин на единицу и обнулить число дюжин

пар. Иначе строка S=NDD∗CDD+ND∗CD+NP∗CP даст неверный результат

РЕШЕНИЕ НЕОПРЕДЕЛЕННЫХ УРАВНЕНИЙ

Неопределенными называются уравнения, в которых имеется два или

более неизвестных, и обычными вычислительными способами они не

решаются. Например, уравнение вида 3x+2y=12.

Такие уравнения, если нет никаких ограничений, имеют бесконечное

множество решений, так как для любого значения одной переменной

найдется соответствующее значение для другой переменной. Например, в

приведенном выше уравнении, каждому значению x соответствует значение

y, которое вычисляется по формуле

312 x

−

= или xy 5.16

−

. Например, при

x=0.5 y имеет значение, равное y=6-1.5·0.5=5.25.

Неопределенные уравнения для целых чисел имеют ограниченное

число решений. При этом х может принимать значения х=0, 1, 2, 3, … Из них

являются решениями только те из них, которым соответствуют целые

значения y.

Рассмотрим целочисленное неопределенное уравнение 3x+2y=12. Оно

имеет следующие решения: 1) х=0, у=6; 2) х=2,

у=3; 3) х=4, у=0. Если даны

ограничения х<>0 и у<>0, то уравнение имеет единственное решение: х=2,

у=3.

10 D=12: DD=D∗D

20 CP=1.05: CD=10.25: CDD=114

30 INPUT N

40 NDD=INT(N/DD)

50 ND=INT((N-NDD∗DD)/D)

60 NP=N-NDD∗DD-ND∗D

70 SP=NP∗CP

80 SD=ND∗CD

90 SDD=NDD∗CDD

100 IF SP>CD THEN NP=0: ND=ND+1

110 IF ND=D THEN ND=0: NDD=NDD+1

120 SD=ND∗CD

130 IF SD+SP>CDD THEN NP=0: ND=0: NDD=NDD+1

140 S=NDD∗CDD+ND∗CD+NP∗CP

150 PRINT "NDD=";NDD;"ND=";ND;"NP=";NP

160 PRINT "S=";S;”$”

- 37 -

Таким образом, решение неопределенных уравнений заключается в

циклических вычислениях значения второй неизвестной переменной при

всех допустимых значениях первой неизвестной. Среди пар значений х и у

решением является пара, в которой обе величены – целые. Рассмотрим задачу

о портном (10 класс, 1996 г.):

Задача. Портной купил x метров красной ткани по цене 13 сом за 1 м.

и y метров синей ткани по цене 17 сом за 1 метр, уплатив за всю покупку

189 сом. Сколько метров той и другой ткани он купил?

Составим уравнение вычисления стоимости покупки: 13х+17у=189.

Допуская, что х и у могут быть равны нулю, определим для них интервалы

допустимых значений: при х=0 17у≤189, то есть у

≤11, при у=0 13х≤189, то

есть, х≤14.

Решение ищется в цикле для х от 0 до 14 или для у от 0 до 11. В

программу включается блок проверки на принадлежность у или х к целым

числам и счетчик числа решений:

C1=13: C2=17: S=189: K=0

FOR X=0 TO 14

Y=(S-X∗C1)/C2

IF Y=INT(Y) THEN K=K+1: PRINT К;“.”;X,Y

NEXT X

PRINT K;“ РЕШЕНИЙ”

Если решений много, их можно запоминать, организовав соответст-

вующие массивы: DIM X(14), Y(11). Выбор единственного решения среди

возможных осуществляется на основе оптимальности, максимальности, про-

порциональности, дизайна и других требований, как, например, в задаче о

разливе сока в разные банки (10 класс, 1997 г.).

Задача. Требуется 19 литров сока без остатка разлить в минимальное

число

банок. Имеются банки емкостью 0,8 и 0,7 литра. Сколько и каких ба-

нок будет использовано?

Задача состоит в том, чтобы разлить весь сок, без остатка, в банки та-

ким образом, чтобы все банки оказались полными. Возможны несколько ва-

риантов решений:

1) 27 банок

– 26 банок по 0.7 и 1 банка по 0.8,

2) 26 банок

– 18 банок по 0.7 и 8 банок по 0.8,

3) 25 банок

– 10 банок по 0.7 и 15 банок по 0.8,

4) 24 банки

– 2 банки по 0.7 и 22 банки по 0.8.

Расход минимального числа банок, как видно отсюда, достигается тем,

что большая часть сока должна быть разлита в банки с большой емкостью.

Отсюда следует основной принцип решения задачи: начинать заполнять по

одному мелкие банки, каждый раз проверяя, не разместится ли остаток сока в

- 38 -

t, с 0 1 2 3 4 5 6 7 8 …

S, м 5 8 12 17 24 32 40 50 64 …

целом числе больших банок. То есть, наливают в одну банку емкостью 0.7 и

следят, чтобы остаток сока делился на емкость больших банок без остатка.

10 REM БАНКИ

20 V1=0.7: V2=0.8: M=0

30 INPUT V

40 N=V/V2

50 IF INT(N)<>N THEN M=M+1:V=V-M*V1: GOTO 40

60 PRINT M;N

В программе использован цикл ПОКА. Это сделано с той целью, чтобы

не упустить случая, когда весь сок может быть сразу разлит без остатка в

большие банки. Например, если бы было дано V=20 литров, то весь сок мож-

но было сразу (без остатка) разлить в 20/0.8 =25 банок. А в цикле ДО, при

первом

проходе, была бы заполнена первая малая банка и затем пришлось бы

остановиться на варианте M=8 и N=18 (26 банок вместо 25).

ПОСТРОЕНИЕ ИЗОБРАЖЕНИЙ И ГРАФИКОВ

Часто на олимпиадах, на практическом туре, участникам предлагаются

задачи на построение рисунков, схем, графиков, диаграмм методами компь-

ютерной графики и мультипликации. Для этого используются графические

операторы и

команды SCREEN, PSET, LINE, CIRCLE, PAINT.

Все участники олимпиады знают принцип построения графиков в про-

цессе циклических вычислений с малым шагом и параллельным построением

на экране соответствующих точек с пересчетом истинных координат на эк-

ранные. Однако это – только полдела. При проверке решения графических

задач особое внимание обращается на правильность построения графиков,

оптимальное использование площади экрана, выбор

масштабов и расположе-

ния координатных осей и др.

Рассмотрим методику построения графиков на экране дисплея. График

– это визуальное отображение аналитической зависимости между величина-

ми. Зависимость может быть задана в виде формулы или таблицы, например:

tvS

или

Первое требова-

ние при решении графиче-

ских задач – это умение

правильно расположить

изображение на экране, то

есть оптимально использо-

вать площадь экрана. Рисунок не должен быть крошечным или огромным, не

помещающимся на экране. В графике должны соблюдаться пропорции, то

есть график не должен быть слишком узким и высоким или

низким и широ-

ким.

- 39 -

Задача построения графиков облегчается, если участник знает или

представляет вид графика, его особенности. Другие участники вначале рас-

считывают и строят график вручную, чтобы затем ввести в программу коор-

динаты начала координат и выбрать масштаб.

Разработку программ построения графиков данных зависимостей, тра-

екторий движения точки, рисунка, чертежа и т.п. следует проводить

в опре-

деленной последовательности:

1. Определение габаритов изображения, то есть установка границ из-

менения переменных величин x

MIN

, x

MAX

, y

MIN

, y

MAX

. Пределы изменения ар-

гумента - x

MIN

и x

MAX

- иногда задаются в условии задачи, иначе их приходит-

ся устанавливать самостоятельно, исходя из особенностей графика, напри-

мер, наличия характерных участков, максимумов, минимумов, перегибов,

разрывов и т.п. Например, в графике параболы наиболее характерной частью

является ее вершина, а в графике синусоиды достаточно показать только 2-3

периода и так далее.

2. Установка

масштабов изображения по горизонтали и вертикали

и М

производится исходя из соответствующих размеров экрана АхВ, вы-

раженных в пикселях. Наиболее часто используемые экранные режимы име-

ют размеры экрана 640х480, 512х256, 480х320. Некрасиво, когда график за-

нимает всю площадь экрана, поэтому желательно отступать от краев экрана

на 5-10 %. С учетом этого масштабы вычисляют по формулам:

MINMAX

−

⋅

8.0

MINMAX

−

⋅

8.0

3. Выбор положения начала и осей координат на экране, то есть на-

чальных координат х

и у

О,

производится, исходя из симметричности или

асимметричности графика относительно осей и начала координат.

4. Организация вычисления и рисования графика на экране. В цикле, с

фиксированным шагом h, при каждом шаге производится вычисление оче-

редного значения аргумента x=x+h, на основе которого вычисляется очеред-

ное значение функции y, а по ним вычис-

ляются экранные

координаты

x=x·M

,·y=M

и рисуется точка на экране,

если график строится по точкам.

5. Пробный запуск программы и

корректировка масштаба, положения

осей координат, внесение изменений в

программу.

Для примера рассмотрим програм-

му построения графика кубической пара-

болы y=x

-3x

+1 на промежутке -1≤ х ≤1 (11 класс, 2001 г.). Соответствующие

разъяснения даны в комментариях программы.

REM ГРАФИК 11КЛ.2001

- 40 -

SCREEN 12: A=640: B=480

CLS

DEF FNF(X)=X^3-3*X^2-X+1

REM УСТАНОВКА КРАЙНИХ ЗНАЧЕНИЙ

XMIN=-1: XMAX=3.5

Y1=FNF(XMIN): Y2=FNF(XMAX)

REM ПОИСК МАКСИМУМА И МИНИМУМА

IF Y1<Y2 THEN YMIN=Y1:YMAX=Y2 ELSE YMIN=Y2:YMAX=Y1

FOR X=XMIN TO XMAX STEP .2

Y=FNF(X)

IF Y>YMAX THEN YMAX=Y

IF Y<YMIN THEN YMIN=Y

NEXT X

REM УСТАНОВКА МАСШТАБОВ

MX=.8*A/(XMAX-XMIN)

MY=.8*B/(YMAX-YMIN)

REM УСТАНОВКА ОСЕЙ КООРДИНАТ

X0=.1*A

IF XMIN<0 THEN X0=X0-MX*XMIN

Y0=.9*B

IF YMIN<0 THEN Y0=Y0+MY*YMIN

LINE (10,Y0)-(630,Y0),15

LINE (X0,10)-(X0 470),15

REM ПОСТРОЕНИЕ ГРАФИКА

FOR X=XMIN TO XMAX STEP.001

Y=FNF(X)

PSET(X0+MX*X,Y0-MY*Y),14

NEXT X

END

Собственно за построение графика отвечают последние четыре строки

программы, а все остальное – подготовительная часть работы, которая обес-

печивает оптимальность и эстетичность экранного изображения. Это - уни-

версальная программа - она пригодна для построения графика любой функ-

ции: достаточно изменить четвертую строку программы, и она сама устано-

вит все необходимые параметры для построения графика

При необходимости, если позволяет время, график можно совершенст-

вовать, например, нарисовать стрелки, добавить обозначения осей, нанести

деления и так далее.

РАБОТА С МАССИВАМИ