Халиуллин Р.Н., Сопуев А. Олимпиады по информатике
Подождите немного. Документ загружается.

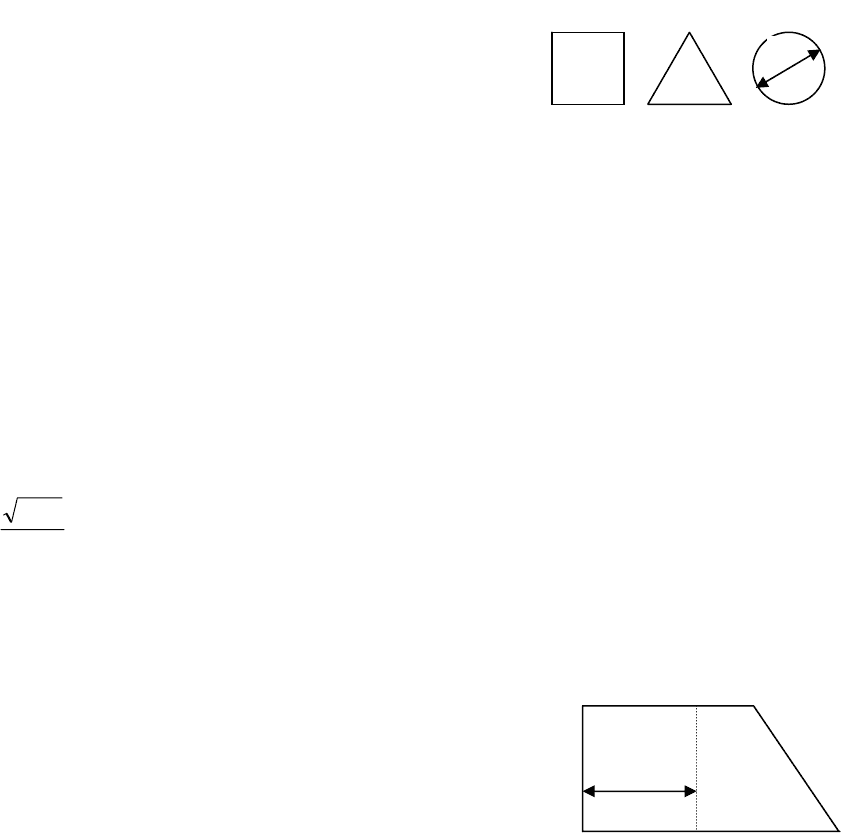
- 21 -
11 КЛАСС
1. Дана последовательность чисел а
1
, а
2
, а
3
, а
4
, …, а
n
, в котором каждое
следующее число получается из предыдущего по формуле
a
i
=a
i-1
+2. Най-
ти сумму первых 15 членов этой последовательности, если
a
1
= -9.
2. Чтобы сшить одну рубашку требуется 1,5 метра ткани, а из 20 сантимет-
ров ткани получается 5 платочков. Имеется К одинаковых кусков ткани
длиной L метров. Сколько рубашек можно сшить из этой ткани и сколько
платочков получится из отходов?
3. Подсчитать, сколько букв использовано для печати слова «информатика».
4. Вывести на экран строку «
я вас люблю» всеми возможными вариантами.
Например, «вас я люблю», «люблю я вас», «я
люблю вас» и так далее.
5. Написать программу для рисования на экра-
не любой из трех геометрических фигур:
Номер и размеры фигуры вводятся с клавиатуры.
6. Разработать диалоговую программу по математике для обучения ученика
младшего класса делению
целых чисел.
IX городская олимпиада по информатике
5 января 1997 г., СШ № 42 им. Керме-Тоо
10 КЛАСС
Теоретический тур
1. Составить блок-схему и алгоритм (программу) решения уравнения
2
4
1
2
+
−
−
=
x
x
y
при значении x, вводимом с клавиатуры.
2. В течение месяца (26 рабочих дней) завод выпускал каждый день на 3
машины больше, чем в предыдущий. Выполнит ли завод план, если в пер-
вый день было выпущено 42 машины, что составляет 67% дневной нор-
мы?
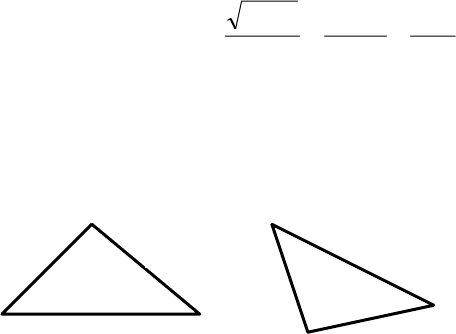
3. Разделить поле на две равные по площади час-
ти с
помощью межи, проведенной параллельно
стороне b. Все стороны, кроме одной, парал-
лельны или перпендикулярны между собой.
Значения a, b, c даны, причем c<a.
4. Требуется 19 литров сока без остатка разлить в минимальное число банок.
Имеются банки емкостью 0,8 и 0,7 литра. Сколько и каких банок будет
использовано?
a
c
x
b
a
a
a
a

- 22 -
5. Найти наименьшее целое число, которое без остатка делится на любое
число от 2 до 9.
6. Дан одномерный массив из N целых чисел. Все нечетные числа перенести
в начало массива, а все четные в конец массива, при этом сохраняя их от-
носительный порядок. Например:
2, 3, 5, 6, 8, 7, 4, 1 → 3, 5, 7, 1, 2, 6, 8, 4
Практический тур
1. Найти сумму всех
чисел таблицы Пифагора (произведений целых чисел от
2 до 9), приведенной на обложке тетради по математике.
2. Представить заданное число в виде произведения его простых множите-
лей. Например: 72 = 1⋅2⋅2⋅2⋅3⋅3.
11 КЛАСС
Теоретический тур
1. Одна корова за сутки съедает A кг сена, одна лошадь –B кг. Составить
программу вычисления наибольшего числа коров, которых можно про-
кормить совместно с L лошадьми в течение N дней. Сколько сена при этом
останется, если запас сена составляет P кг?
2. В одном из двух 10-литровых ведер находится
9 литров горячей воды при
температуре 95°С, а в другом –10 литров холодной воды при температуре
15°С. Как получить 10 литров воды с температурой 39°С, если под рукой
нет другой посуды и выливать воду нельзя?
3. Дано строковое выражение. Проверить, есть ли в нем два одинаковых
символа, стоящие рядом? Например: “классная доска”.
4.
В данном предложение при печати удалить все гласные буквы (а, е, и, о, у,
ы, э, ю, я). Например: “математика ” → “мтмтк”.
5. Найти решение уравнения x
2
-7x+5=0 на отрезке от 0 до 2 с точностью
0,001.
6. Создать квадратную матрицу с нечетным числом
строк, в котором элементы лежащие на главной
диагонали равны единице, на другой диагонали
равны двум, элемент на пересечении диагоналей
равен трем, а остальные элементы равны нулю.
Например, как показано справа.
Практический тур
1. Создать программу «Часы
» в любом варианте (цифровом или графиче-
ском).
1 0 0 0 2
0 1 0 2 0
0 0 3 0 0
0 2 0 1 0
2 0 0 0 1
- 23 -
2. Организовать на экране «бегущую» строку рекламного объявления
«ИЗУЧАЙТЕ ИНФОРМАТИКУ!».
X городская олимпиада по информатике
3 января 1998 г., СШ № 4 им. Панфилова
10 КЛАСС
1. Вычислить значение переменной y при заданном значении переменной x:
)
1
1
42
1
(:
1
1
3
−
−
−+
−
=
xxx
x
y
2. Из одного аила выехал всадник со скоростью V
1
. Через T
1
часов после это-
го из другого аила выехал навстречу ему другой всадник и через Т
2
часов
они встретились. Расстояние между аилами S км. Составьте алгоритм вы-
числения скорости второго всадника.
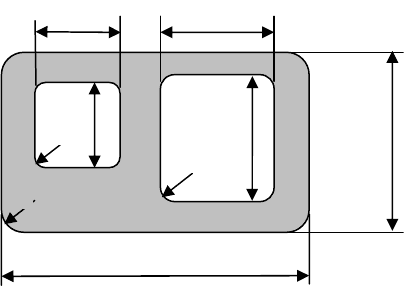
3. Даны два треугольника со сторо-
нами a, b, c и m, n, p. Равны ли
эти треугольники? Данные пред-
ставлены в виде списка: 25, 35,
40, 35, 25, 45.
4. Дано натуральное число n=5. Вычислить сумму
S=1⋅2 + 2⋅3
⋅4 + 3⋅4⋅5⋅6 + 4⋅5⋅6⋅7⋅8 +…+ n(n+1)(n+2)…2n
5. Правильно ли составлена программа?
S=0: P=1
FOR I=1 TO N
FOR J=1 TO N
P=P∗J
NEXT I
S=S+P
NEXT J
PRINT S
6. Даны два одномерных массива A и B, состоящие из одинакового числа
элементов. Один массив упорядочить по возрастанию, другой – по
убыванию и сложить поэлементно в один массив. Является ли новый
массив упорядоченным? Новой массив не заводить.
11 КЛАСС
1. Два автомобиля, находясь в момент включения секундомера на расстоя-
ниях S
1
и S
2
от перекрестка, движутся к перекрестку по взаимно перпенди-
кулярным направлениям со скоростями V
1
и V
2
м/c. В какой момент време-
p
a c
b
m
n
- 24 -
ни расстояние между автомобилями было минимальным? Определить с
точностью до секунды.
2. В данном предложение подсчитать, сколько раз встречается сочетание
«он» или «но». Один символ в два сочетания входить не должен, напри-
мер «оно» должно засчитываться как одно сочетание, а «онно» – как два.
3. Дано натуральное трехзначное число n. В
каком случае оно больше: если
читать слева направо или справа налево? В каком порядке нужно переста-
вить цифры, чтобы получить максимально возможное число?
4. Точка участвует одновременно в двух колебаниях во взаимно перпенди-
кулярных направлениях по законам X=X
m
⋅
sin(3t) и Y=Y
m
⋅
cos(2t). Нарисо-
вать на экране траекторию движения точки в течение Т сек. Принять
X
m
=100, Y
m
=100.
5. Дана двухмерная матрица размером M х N, состоящая из целых чисел 1, 2
и 3, но один из элементов равен нулю. Необходимо элементы, окружаю-
щие этот элемент, сделать равными 4. Вывести массив на печать.
6. Нарисовать на экране дисплея движение молекулы идеального газа в
плоском прямоугольном сосуде сечением a х b, если даны составляющие
начальной скорости V
x
и V
y
. При ударе о стенку соблюдается закон отра-
жения – угол падения равен углу отражения.
XI городская олимпиада по информатике
3 января 1999г., СШ № 42 им. Кирова
10 КЛАСС
1. Вычислите свой возраст в днях, со дня рождения по сегодняшний день.
Считать, что в году 360 дней, а в каждом месяце 30 дней.
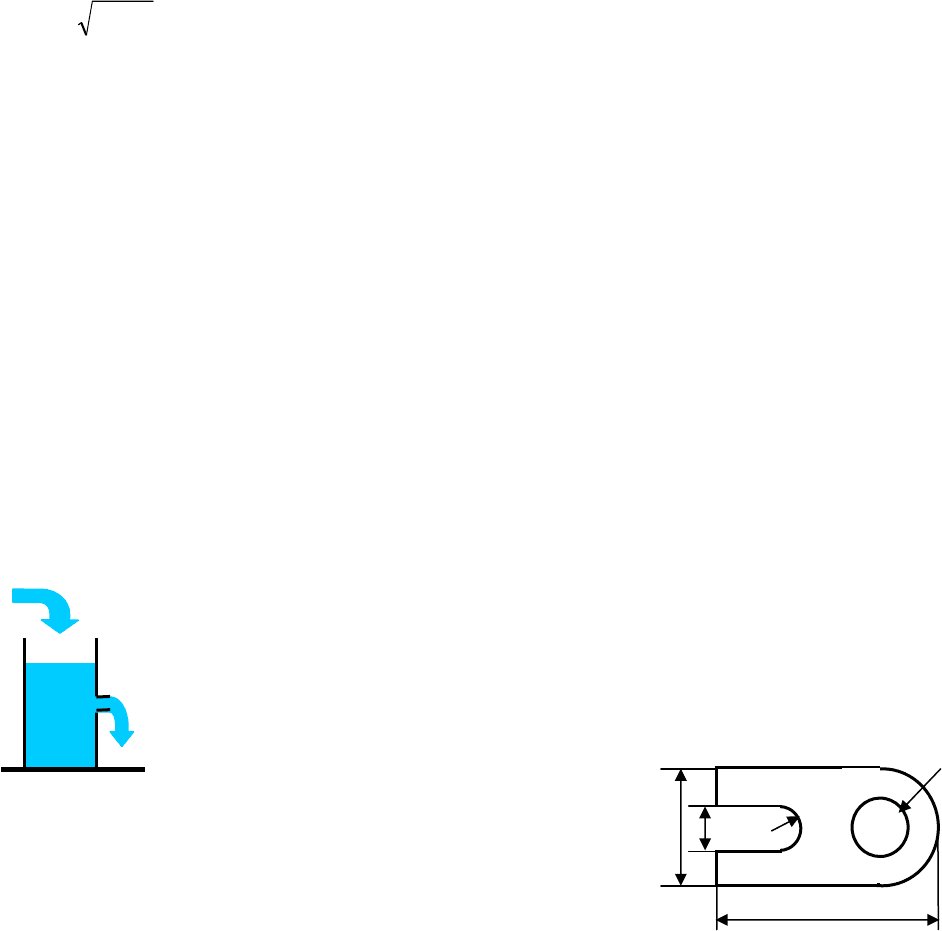
2. Найти площадь металлической пла-
стинки с заданными размерами сто-
рон и радиусов закруглений: a, b,
r, a1, b1, r1, a2, b2, r2.
3. Даны четыре отрезка длиной a, b
,
c, d метров. Можно ли из них по-
строить выпуклый четырехуголь-
ник? Если да, то можно ли постро-
ить прямоугольник или квадрат?
4. На два стула могут сесть 3 ученика. Сколько учеников смогут разместить-
ся в зале, где стулья расположен в К рядов, причем в первом ряду распо-
ложено 10 стульев, а
в каждом следующем ряду на один стул больше, чем
в предыдущем?
r
r2
r1
a1 a2
a
b
b2
b1

- 25 -
5. Как набрать в детскую ванну 40 литров теплой воды с температурой 40°С,
если имеются две бочки с воды с температурой 30°С и 45°С, а также точ-
ный термометр и кружка ёмкостью 0,4 литра.
6. Дан одномерный массив из N целых чисел. Среди них есть числа, которые
делятся на 3 или 5 или вообще не
делятся ни на 3, ни на 5. Создать три но-
вых массива: чисел, которые делятся на 5, делятся на 3 и все остальные.
Например:
13, 5, 9, 7, 6, 15, 4, 1 → 5, 15
9, 6, 15 13, 7, 4, 1.
11 КЛАСС
1. Некто решил разбогатеть на бирже, где ежедневная прибыль может соста-
вить от 10% до 20% от вложенных денег, но в то же время сохраняется
риск проиграть за один день от 5% до 15%. Составить модель игры на
бирже в течение одного месяца (30 дней), если человек в первый день
имел S сом денег, а каждый
следующий день он вкладывал, все что имел.
Ежедневно за вход на биржу нужно платить S1 сом.
2. Во введенном с клавиатуры слове переместить гласные буквы по кольцу.
Первую гласную переместить на место последней гласной, а остальное
передвинуть вперед. Например: «литература» → «летарутари».
3. Преобразовать введенное строковое выражение в выражение с «
западным
акцентом», заменяя звонкие согласные на глухие и наоборот. Например:
«город ОШ» → «корот Ож». Пары звонких и глухих согласных (Б-П, В-
Ф, Г-К, Д-Т, Ж-Ш, З-С, Ц-Ч).
4. Построить график функции у=х
3
-20х-10 на промежутке -5≤ х ≤7.
5. Бригада грузчиков может за один рабочий день (с 8.00 до 16.00) может
разгрузить 6 вагонов. Ежедневно, к началу смены на разгрузку подается от
3 до 9 вагонов. В субботу бригада не уходит с работы до тех пор, пока не
будет разгружен последний вагон. В какое время в
субботу грузчики за-
кончат работу?
6. Дана двухмерная матрица целых двухзначных чисел, размером M×N (M
строк и N столбцов). Получить «зеркальную» матрицу, в которой в каждой
строке элементы расположены в
обратном порядке, как, например,
показано справа.
XII городская олимпиада по информатике
9 января 2000 г., СШ № 42 им. Керме-Тоо
1 2 3 4 4 3 2 1
5 6 7 8 8 7 6 5
9 10 11 12 12 11 10 9
- 26 -
10 КЛАСС
1. Составить блок-схему и алгоритм (программу) решения уравнения
2
9 xy −=
. Значение х вводится с клавиатуры, а результат выводится на
экран дисплея.
2. Один автомобиль перевозит за 1 час 15,6 т груза, а другой – на 3,2 т мень-
ше. Сколько тонн груза перевезут оба автомобиля за 8 часов, работая вме-
сте?
3. В восьми старших классах учится: 12, 17, 13, 9, 15, 19, 21 и 8 мальчиков.
Сколько девочек учится в старших классах, если
общее число старше-
классников в школе составляет 247 человек?
4. За электроэнергию введена дифференцированная оплата. За каждый кило-
ватт-час до 150 квт.ч. нужно платить по 17 тыйынов, за каждый квт.ч
свыше 150 нужно платить 25 тыйынов, а за каждый квт.ч свыше 300 – 50
тыйын. Сколько денег нужно заплатить за израсходованную электроэнер-
гию, если известно
начальное и конечное значение счетчика А и В.
5. Некто съедает в первый день одну булку, на следующей день - две, на тре-
тий день - три булки, а на четвертой день - голодает. Сколько булок он
съест за 18 дней?
6. Хозяин решил наполнить водой 200 литровую бочку с
открытым верхом и поставил ее под
кран, дающий в минуту
50 литров воды, но забыл закрыть горловину бочки, через
которую может вытекать в минуту 30 литров. За сколько
минут бочка наполнится до краев?
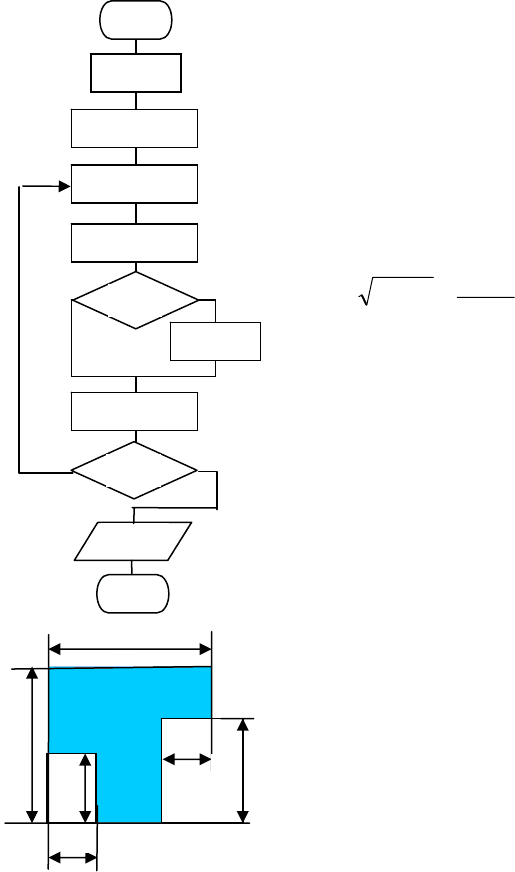
7. Пользуясь графическими операто-
рами, нарисовать прокладку с габаритами 400 х
800 мм. Расстояние между центрами 400 мм. Ос-
тальные размеры произвольные.
11 КЛАСС
1. Болотбек ходит в школу со скоростью 80 м/мин. Он выходит из дома в
06.50 и приходит в школу в 07.15. На каком расстоянии от школы живет
Болотбек?
2. Дано натуральное многозначное число А. Найти и сравнить в нем число
четных и нечетных цифр. Число 0 считается четным.
3. Найти самое длинное слово
в предложении А$, введенном с клавиатуры, и
вывести его на экран.
800
400
- 27 -
4. Деталь считается годной, если ее масса отличается от эталонной не более,
чем на ±3 грамма. Контролер, вместо того, чтобы взвешивать на весах
каждую деталь отдельно, стал сравнивать массы деталей попарно. Если
разность масс оказывалась больше 3 грамм, он выдавал сообщение: «есть
брак». В таблице приведены массы 10 деталей, последовательно посту-
пивших на
проверку: 13, 11, 9, 8, 10, 12, 14, 13, 15, 18. Было ли сообщение
о браке? Как должен был поступать контролер, чтобы наверняка сооб-
щать, что брака нет?
5. Дана квадратная матрица из N х N целых чисел, имеющих случайные зна-
чения от 1 до 9. Каких чисел больше в данной матрице? Оставить только
их, заменив остальные нулями.
6. Крестьянин, распахав участок
земли 100х80 м, решил ежегодно увеличи-
вать ее площадь. В первый год он увеличивает ширину на 30 м, на сле-
дующий год – длину на 15 метров. Через сколько лет площадь участка
увеличится в 2 раза? Каковыми станут периметр и площадь участка?
XIII городская олимпиада по информатике
16 января 2001г., СШ № 42 им. Керме-Тоо
9 КЛАСС
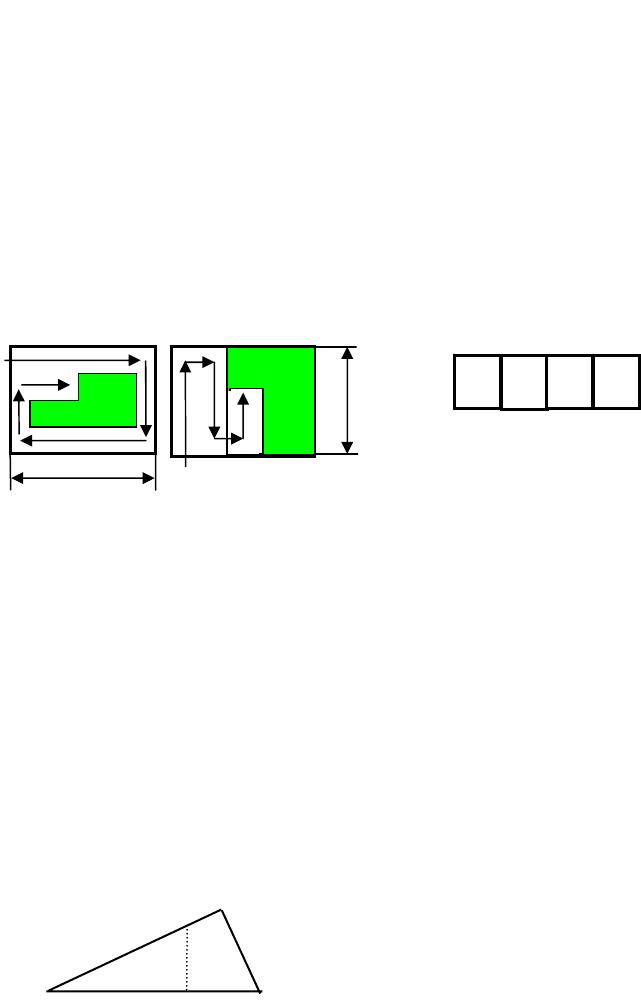
1. Проанализировать работу приведенной блок-схемы
и записать алгоритм на любом алгоритмическом
языке. Сообщить результат выполнения алгоритма.
2. Составить алгоритм вычисления выражения
1
1
5
2
2
−
−+=
x
xy . Ввод х с клавиатуры.
3. В пяти старших классах учится 21, 17, 13, 19 и 12
мальчиков. Сколько девочек в этих классах, если в
каждом классе учится по 30 учеников?
4. Даны три числовые величины А, В, С. Составить
алгоритм обмена значениями, чтобы значения А, В,
С оказались в порядке убывания, то есть А>В>С
.
Например А=7, В=5, С=12 → А=12, В=7, С=5.
5. Составить алгоритм вычисления площади пластин-
ки. Величины а, b, m, n, x, y вводятся с клавиатуры. На
экран вывести площадь пластинки.
10 КЛАСС
R = 2
N=R
∗
R-R
R=R-2
N=N-R
R<-4
нет
да
R = -R
K=R
∗
4
K=N
нет
да
Выв R
кон
нач
b
a
x
n
m
y
- 28 -
1. Проанализировать содержание и работу приведенной программы и сооб-
щить результат его выполнения.
2. В центре экрана размером 200х200 нарисовать
квадрат с вписанной и описанной окружностями.
Сторона квадрата равна 50 пикселям.
3. Дан массив из 2N целых чисел. Сократить массив
вдвое, последовательно заменяя каждую пару чисел
одним элементом массива, равным их сумме
.
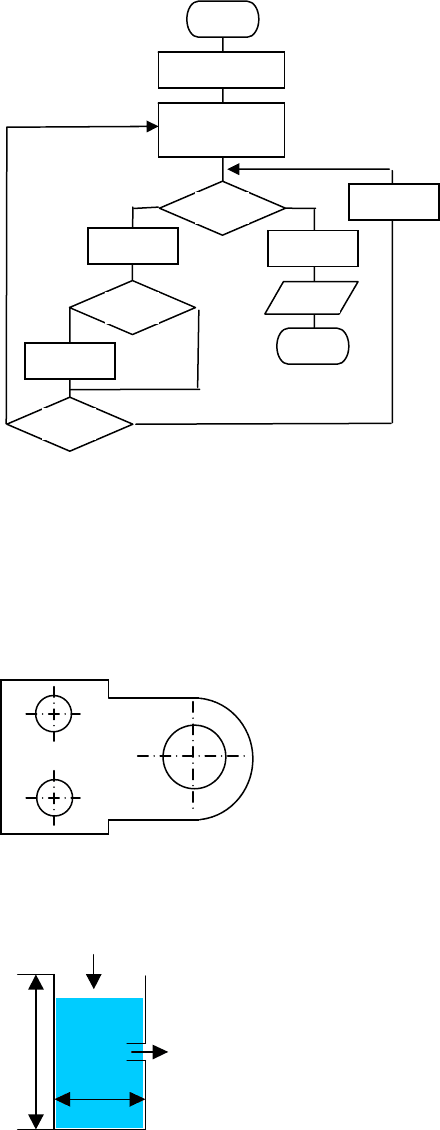
4. Каким способом быстрее постричь траву на ста-
дионе размерами АхВ? Косилка скашивает полосу
шириной Н со скоростью V. На повороты затрачи-
вается время Т1 (на 90
0
) и Т2 (на 180
0
).
5. Исполнитель
записывает в
каждую из 4 клеток любую цифру от 2 до
4. Сколько различных четырех-значных
чисел можно записать таким образом?
11 КЛАСС
1. Подсчитать число гласных букв в строке А$. Преобразовать строку, уда-
лив все гласные буквы, например:
”МАТЕМАТИКА” → ”МТМТК”
2. Даны две строки А$ и В$. Определить, сколько у них общих символов.
Например, строки “информатика” и “физика” имеют 4 общих символа: и,
ф, к, а.
3. Построить график функции у=х
3
-3х
2
+1 на экране дисплея. Интервал значе-
ний x выбрать самостоятельно.
4. Поле имеет форму прямоугольного треугольни-
ка. Разделить это поле на две равные по площади
части с помощью межи, проведенной на рас-
стоянии х от вершины А, перпендикулярно гипо-
тенузе АС. Две стороны треугольника b и c даны.
5. Двое бросают
по две кости (два кубика). Выпавшие очки суммируются. В
случае равенства очков бросание повторяется. Побеждает тот, кто первым
наберет 100 очков. Разработать программу игры.
XIV городская олимпиада по информатике
9 января 2002г., СШ № 42 им. Керме-Тоо
P=2
DIM AB(4,4)
FOR K=1 TO 4
FOR M=1 TO 4
AB(K,M)=M
NEXT M
NEXT K
FOR K=4 TO 1 STEP-1
P=P+AB(K,K)+AB(4,K)
NEXT K
PRINT P
END
А
В
4
3
2
2
c
В
А
С
b
- 29 -
9 КЛАСС
1. Вычислить сумму двух шестнадцатеричных чисел:
S=&H1A +&HFC
и записать результат в шестнадцатеричной и десятичной системах. Сколь-
ко бит и байтов содержит запись этого числа?
2. Турист в первый день прошел пешком 10 км и решил каждый день прохо-
дить на 1 км больше. За сколько дней он преодолеет 100 км?
3. Имеются 4 бочки
. Первая, емкостью
24 ведра, до краев наполнена мас-
лом. Как разделить это масло на три
равные части, если другие бочки
имеют емкость 5, 11 и 13 ведер?
4. Проанализировать блок-схему алго-
ритма и сообщить результат, кото-
рый будет выведен. Написать про-
грамму на языке Бейсик.
5. Некто, вспахав участок земли раз-
мерами 200 х
100 м, решил ежегод-
но увеличивать его ширину на 50%.
Через сколько лет площадь участка
увеличится в 9 раз, и чему будет ра-
вен периметр участка?
10 КЛАСС
1. Найти все трехзначные числа, которые при делении на 2 дают остаток 1,
при делении на 3 - остаток 2, при делении на 4 - остаток 3, а само число
делится на 5.
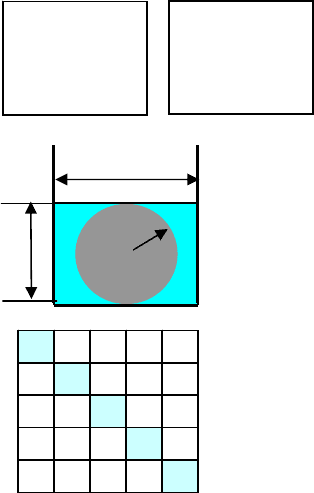
2.
С помощью графических операторов составить
программу для рисования чертежа детали - ушка на
экране дисплея. Размеры произвольные.
3. Уголь добываемый в пункте A продается по q сомов
за тонну, а добываемый в пункте B- на p процентов
дороже. Пункты A и B соединяет дорога длиной l км. B какой зоне
расположены потребители угля, для
которых возить уголь из пункта B
дешевле, чем из пункта A, если перевозка 1 тонны угля на расстояние 1 км
обходится в r сомов?
4. С точность до 0,0001 на отрезке 0…2 найти корни
уравнения 2x
2
-6x+4=0.
да
нет
A=A-B
B
=A-
B
A=B
нет
да
нач
A=7, B=12
B=-B
A=B-A
A<B
B>0
нет
да
B=A-1
A=A+B
A
кон
H
B
A
D
- 30 -
5. В пустую цилиндрическую бочку высотой H метров и диаметром
основания D метров, сверху наливается вода со скоростью A литров в
минуту. На середине высоты бочки расположено отверстие, через которое
ежеминутно может выливаеться B литров. Какого максимального уровня
может достигь вода в бочке, если скорость вытекания воды через
отверстие пропорционально высоте
жидкости над отверстием: B=kh, где k
– коэффициент пропорциональности. Через какое время уровень воды
достигнет максимума? Значения H, D, A, k вводятся с клавиатуры.
11 КЛАСС
1. Дана таблица B, состоящая из M строк и N столбцов. Составить программу
для обмена местами наибольшего и наименьщего элемента таблицы.
2. С любым
числом, записанным на доске, разрешается производить
следующие действия: стирать последнюю цифру; заменять числом, вдвое
большим. Как с помощью таких операций из числа «458» получить число
«14»?
3. По углам текстового экрана (24 строки по 64
позиции) расположены символы “О”, ”И”, ”В”,
”Т”. Переместить символы в центр экрана,
чтобы получился квадрат из четырех
символов. При
этом на экране должны остаться следы
перемещения каждого символа.
4. В цилиндрический сосуд с диаметром основания D см
налита жидкость высотой H см. В жидкость опускают
шар, который погрузившись, одновременно касается дна
и поверхности жидкости. Найти радиус шара R с
точносью до 0,01 см.
5. Таблица футбольного чемпионата задана матрицей
N∗N, в которой все элементы по главной диагонали
равны нулю, а остальные элементы равны 0, 1 или 3 (3 -
выигрыш, 1 – ничья, 0 – проигрыш). Найти команду -
победителя чемпионата и число команд, у которых число побед больше
числа поражений.
КАК РЕШАТЬ ОЛИМПИАДНЫЕ ЗАДАЧИ
Олимпиадные задачи внешне выглядят как простые школьные задачи.
Поэтому некоторые участники начинают сразу составлять соответствующую
программу, которая при тестировании начинает давать сбои и ошибки. Дело
в том, что олимпиадные задачи, как правило, имеют «двойное дно», то есть
они имеют подводные камни и ловушки, которые можно обнаружить только
О И
В Т
ОИ
ВТ
0 1 0 3 1
1 3 1 3 0
3 0 0 0 1
0 3 0 0 0
1 1 1 3 0
D
H
R
